Распределение частиц в вертикальном вихревом потоке газа

Автор: Кузнецов Г.Ф.

Рубрика: Физика

Статья в выпуске: 7 (62), 2006 года.

Бесплатный доступ

Работа посвящена исследованию распределения твердых частиц, движущихся в закрученном газовом потоке.

Короткий адрес: https://sciup.org/147158472

IDR: 147158472

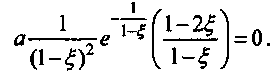
Список литературы Распределение частиц в вертикальном вихревом потоке газа

Ферцигер Дж., Комер Г. Математическая теория процессов переноса в газах. -М.: Мир, 1976. -554 с.
Прохоров A.M. Физический энциклопедический словарь. -М.: Советская энциклопедия, 1983.-928 с.
Пайерлс Р.Е. Квантовая теория твердых тел. -М.: Мир, 1956. -340 с.
Кузнецов Г.Ф. Физико-химические процессы и технология газификации при сжигании твердых топлив. -Челябинск: Изд-во ЮУрГУ, 2002. -174 с.

Краткое сообщение