Распределение давления в суставном зазоре человека при наличии упругого хряща и зависимого от времени магнитного поля

Во многих статьях, представленных в списке литературы, обсуждаются не только гидродинамические параметры (т.е. компоненты скорости синовиальной жидкости, давление в зазоре сустава), но также механические параметры (а именно, силы трения, коэффициент трения, несущая способность). В этих работах, как правило, используются аналитические и численные методы. Краткий обзор разработанных методов и результатов решений обобщен в таблице.

В работах [24, 26, 30-34] предлагаются методы решения при наличии силы трения в различных суставах человека при различной геометрии суставных поверхностей костей. При этом рассматриваются переменная толщина зазора сустава, а также несимметричное течение синовиальной жидкости в магнитном поле.

Таблица

Краткий обзор работ в области параметров тазобедренного сустава

Статья	Течение синовиальной жидкости		Гидродинамическое трение, исследованное методом		Магнитное поле	Рабочие параметры, полученные аналитическим (а) и численным методом (б)
	симметричное	несимметричное	сдавливания	вращения
[2]	да	нет	да	да	нет	давление (а), силы трения (a), коэффициент трения
[11]	да	нет	да	нет	нет	силы трения
[16]	не определено	не определено	не определено	не определено	да	наличие смазки
[19]	да	нет	нет	да	нет	давление, несущая способность (а), (б)
[21]	да	нет	нет	да	нет	сила трения, несущая способность, коэффициент трения (а), (б)
[22]	да	нет	нет	да	нет	распределение давления, несущая способность (а), (б)
[23]	да	нет	нет	да	нет	полные решения (а), (б)
[24]	да	нет	нет	да	нет	сила трения (а)
[25]	да	нет	нет	да	да	сила трения (a)
[26]	да	нет	нет	да	да	сила трения (a)
[27]	да	да	да	да	да	распределение давления (a)
[28]	да	да	нет	да	да	распределение давления (a)
[29]	да	нет	да	нет	нет	распределение давления (a)
[30]	да	нет	да	нет	нет	сила трения (a)
[31]	нет	да	да	нет	нет	распределение давления (а), скорость синовиальной жидкости (a)
[33]	нет	да	да	нет	нет	распределение давления (a)

При производстве вычислений сил трения в суставах человека учитываются компоненты скорости в окружном и продольном направлении [34]. Проблема вычисления несущей способности сустава человека при переменной деформируемой толщине зазора сустава и для несимметричного течения синовиальной жидкости в магнитном поле не обсуждалась в предыдущих работах автора [25-28, 31, 33-34].

Новыми элементами, представленными в данной статье, являются вычисления распределения давления в тазобедренном суставе человека для деформируемой поверхности хряща и кости в криволинейных ортогональных координатах. Между поверхностями имеется несимметричное течение в присутствии нестационарного магнитного поля.

• 2.    Формулировка проблемы

В данной статье учитываются следующие факторы:

• •    вращательное движение головки бедренной кости и движение сдавливания головки кости,

• •    несимметричное движение синовиальной жидкости с постоянной плотностью,

• •    стационарное и изотермическое течение жидкости,

• •    переменная динамическая вязкость синовиальной жидкости,

• •    переменная толщина зазора сустава человека,

• •    переменное по времени индуцированное магнитное поле.

Поверхности головки кости и суставной чашечки покрыты тонким слоем хряща. Толщина хрящевой ткани на поверхности головки кости изменяется от 0,9 до 2,1 мм. Толщина слоя хрящевой ткани на поверхности чашечки варьируется от 0,5 до 2,1 мм. Изменения толщины зазора сустава могут быть связаны с геометрией головки кости, а именно, с некоторыми нерегулярностями, вызванными локальными деформациями хряща, шероховатостью и неровностью поверхностей хрящевой ткани. Упругогидродинамические эффекты могут рассматриваться в нормальных суставах человека из-за больших усилий, имеющих место в некоторых видах спорта, или в случае патологических суставов, когда из-за гидродинамического давления могут возникать деформации хрящевых поверхностей.

Биоупругие и гидродинамические эффекты имеют место из-за гибких и конформных пленок смазки с переменной толщиной и с переменной вязкостью. Ткань хряща приспосабливается к условиям реальной смазки и, тем самым, создает интеллектуальную систему смазки. Шероховатость и неровности поверхности хрящевой ткани в чашечке и в головке кости представлены на рис. 1. Кроме того, мы учитываем патологические нерегулярности поверхности кости из-за шероховатости и различных изменений поверхности, характерных для многих заболеваний [17]. Среднеарифметическая шероховатость поверхности головки кости имеет значения от 0,82 до 2,52 мк, а для чашечки диапазон значений составляет от 1,99 до 3,88 мк [15]. При заболеваниях соответствующие значения могут составлять от 10 до 35 мк.

Сферические поверхности кости в тазобедренном суставе создают криволинейный сферический зазор сустава. На рис. 2 показана сила нагружения С z в тазобедренном суставе человека, возникающая между поверхностями в магнитном поле при наличии гидродинамической смазки из-за вращения головки кости в окружном или меридиональном направлении. Значения магнитного поля индукции периодически меняются со временем. Вращательное движение головки кости радиуса R с угловой скоростью ω вызвано движением конечностей человека.

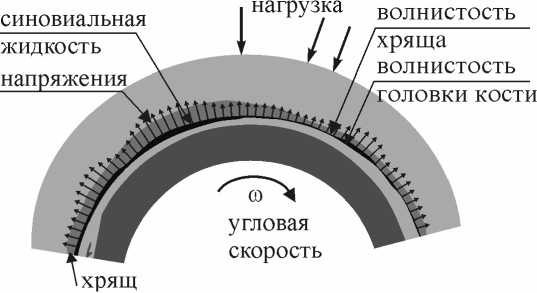
Рис. 1. Неровности поверхности кости и суставных чашечек, покрытых хрящем, в тазобедренном суставе человека

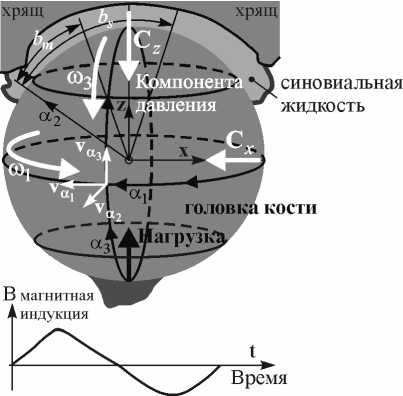
Рис. 2. Сила С _z, возникающая в тазобедренном суставе человека в сферических координатах при гидродинамической смазке с вращением как сила, противоположная действию силы нагружения (зазор в увеличенном масштабе)

На рис. 3 показана сила нагружения С z в тазобедренном суставе человека при наличии гидродинамической смазки с движением сдавливания головки кости в указанном направлении. Произвольные вращательные поверхности кости создают криволинейный зазор сустава там, где есть синовиальная жидкость. На рис. 3 показаны две поверхности кости при сдавливании синовиальной смазки в суставах человека в магнитном поле индукции. Две криволинейные поверхности кости, отделенные зазором сустава малой толщины, поднимаются с однородной скоростью U. Эта скорость вызывается движением конечностей человека.

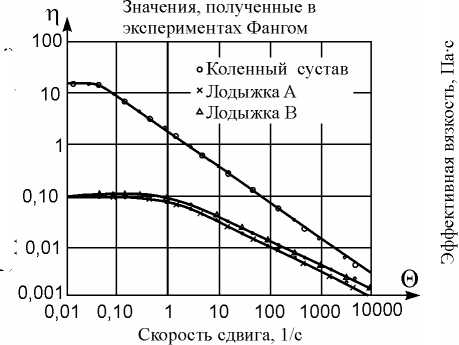
Соотношения между динамической вязкостью синовиальной жидкости и скоростью сдвига представлены на рис. 4. На рис. 4а показаны вязкости жидкости в голеностопном и коленном суставах, изученные с помощью реогониометра Вайсенберга при вращательном движении. На рис. 4b,c представлены численные и экспериментальные значения для синовиальной жидкости из работ [3, 4, 5]. При малых скоростях сдвига коэффициенты эффективной вязкости постоянны и жидкость имеет свойства ньютоновской жидкости. При больших скоростях сдвига коэффициенты убывают при увеличении скорости сдвига. Теоретические аспекты определяющих соотношений для синовиальной жидкости обсуждаются в работе [5].

Синовиальная жидкость

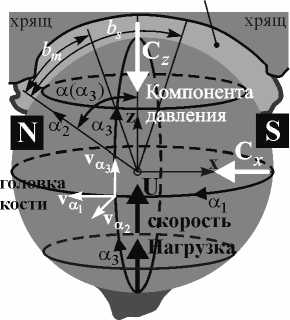
Рис. 3. Сила С z , возникающая в тазобедренном суставе человека в сферических координатах при гидродинамической смазке с выдавливанием как сила, противоположная действию силы нагружения (зазор в увеличенном масштабе)

Эффективная вязкость. Па-с

а

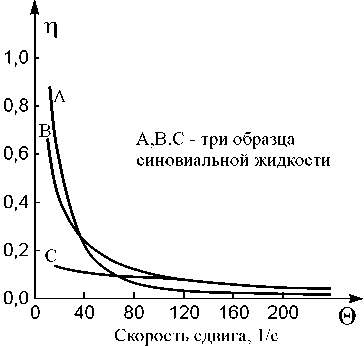
б

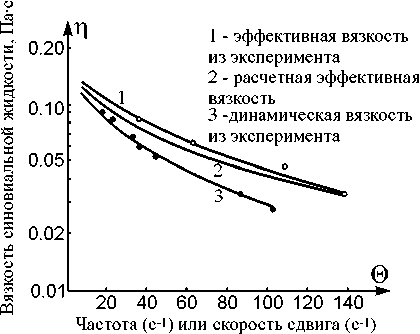
с

Рис. 4. Зависимость динамической вязкости синовиальной жидкости от скорости сдвига

• 3.    Уравнения Максвелла для нестационарного электромагнитного поля

Уравнения Максвелла для нестационарного электромагнитного поля имеют вид [13]:

rotH = o E ⁺ d ”, rot E ⁼ -^у’ div B - 0, div D = p e , div ( rotH ) = div f o E ' ^Д 1- 0,

где D = eE - объемный электрический заряд в синовиальной жидкости в Ас/м3, D -вектор электрической индукции Ас/м2, E - вектор напряженности электрического поля в мкгс 3 А, о - коэффициент электропроводности синовиальной жидкости в с3А2м-3кг, Нi - компоненты вектора напряженности магнитного поля в А/м, Bi = ц H, - компоненты вектора магнитной индукции B в Т, N, = хНt - компоненты вектора намагниченности N в А/м, ? - коэффициент магнитной проницаемости синовиальной жидкости в мкгс-2 А-2, e - коэффициент электрической проницаемости синовиальной жидкости в с4А2м-3кг, х - безразмерный коэффициент интенсивности намагничивания.

При однородных и изотропных свойствах синовиальной жидкости без объемных электрических зарядов при ре=0 уравнения (1) имеют следующий вид:

rotH -o E + E^d E , rotE --ц^Д , div H = 0, div E = 0, |о + еД| div E = 0. (2) d t         d t                  Id t ]

Учитывая тождество rot (rot R) = grad(div R) - V2R,

уравнения (2) приводятся к следующей системе дифференциальных уравнений в частных производных гиперболического типа:

;         8H     82 H    2 _     8E

V ² H -цо—--+ ЦЕ —— , V ² E -цо——+ ЦЕ—— .

d t        812                  9t5

Если синовиальная жидкость есть хороший изолятор (при условии о = 0), то из (4) получим:

V2 H-це^^Д, V2 E-це^.(5)

д t ²

Для электропроводящей синовиальной жидкости (при условии о >>  e » 0) из (4) следует:

V2H -ЦО^Д, V2E u^d E .(6)

d t                  о t

• 4.    Основные уравнения для течения синовиальной несжимаемой микрополярной жидкости в деформируемом зазоре сустава

Течение синовиальной несжимаемой микрополярной жидкости в деформируемом зазоре сустава описывается уравнениями неразрывности, сохранения количества движения, момента количества движения синовиальной жидкости и уравнением для перемещения упругого хряща в следующем виде [6, 8]:

div v =0,

p d v/ dt = - grad p +( n + n r ) A v+ n r rot Q ,

p m r d Q dt = 2 n r Q + n r rot v H v rot (rot Q )'( n_a ■ П_в ■ П ? ) grad ( div Q ),          (9)

G A u +( G + Л ) grad ( div u) p * 5 2 u 5 1 ²,                       (10)

где приняты следующие обозначения: Ω – вектор микровращения в 1/с, η– динамическая вязкость в Пас, η r – динамическая вязкость микровращения в Пас, η α , η β , η γ – коэффициенты угловой вязкости в Нс, m r –момент инерции жесткой частицы в м², v – вектор скорости синовиальной жидкости в м/с, p – давление в Па, ρ – плотность синовиальной жидкости в кг/м³, A - оператор Лапласа в м², u -вектор перемещения хряща в м, t – время в с, ρ^* – плотность хряща в кг/м³. Мы также обозначаем: G =0,5 E (1+ν)^-1 – модуль сдвига хряща в Па, Λ= E ν(1+ν)^-1(1+2ν)^-1 – коэффициент упругости Ламе в Па, E - модуль Юнга хряща или кости в Па, v - коэффициент Пуассона хряща или кости.

Мы учитываем следующие порядки величин чисел Рейнольдса для микровращения:

Re . V080p = о(1), Re . Vo£oP = о(1), Re . Vo£oP = o(1),

По +П r                 П r и пренебрежимо малые модифицированные числа:

Re„6- V080P << 1, Rey V080 mP << 1,(12)

e na+np где T . 80/R * 10-3, T . 8s/R * 10-3. Здесь R - радиус кривизны поверхности кости в м,

8 0 - характеристическое значение толщины зазора в м, 8 s - характеристическое значение толщины хрящевого слоя в м, V0 – линейная или окружная скорость поверхности кости в м/с, Основные уравнения (7)–(10) после пренебрежения членами порядка T и T* имеют следующий вид [8]:

—

0-—Г ^Tp h1 5 a1

5 ² v j      5Q₃

^{+ ( n} o ⁺ⁿ r ) ^ ⁺ⁿ r 00 3 ,

0-^, 5а 2

2 1   ⁵ h l

P v1 К h hз да з h3 ^

5a 1

—

1 5 p , .5² v₃ Т" я— ^{+ (}П o +П r )— 3 ^h 3 ^5a 3 5a ²

1 1 5 v-i + hh₃ -—

5a 2

5 2Q3

П у       ''

5a 2

5 ² Q

П у ^да 2

—

—

'.2 _; ⁽ h ^v з ^)- °

П r

+n

5a 2     '

, ^V 3- = 0

^{1 r} -a .     ⁰¹

5 ² Q 2 5a ²

- 0,

5Q, Пг я— , 5a 2

^5a 2

5 u

^{( 2} G ⁺ ^   , a2

^- 8 2 i

^(з K a t T *) 5 a 2

, i , j = 1,2,3,

где h 1 , h 3 - коэффициенты Ламе и 0 < a _i = ф <  2 п c 1 , 0 < c 1 < 1, b m =п R /8 < a ₃ = 9 < п R /2 = b s , 0 < a ₂ = r < £ . Мы обозначаем: K = Л + (2/3) G - объемный модуль упругости в Па, a _T -коэффициент линейного температурного расширения хряща или кости в К^-1, T ^* – температура в хряще в К, б у - символы Кронекера (1 для i = j и 0 для i * j ). Мы применяем криволинейную ортогональную систему координат a i , a ₂, a ₃ в окружном направлении, по толщине зазора и по длине, соответственно. Символы u 1 , u 2 , u 3 означают неизвестные компоненты вектора перемещения тела хряща в окружном направлении, по толщине зазора и в меридиональном направлении, соответственно. При аксиально несимметричном течении синовиальной жидкости три неизвестные компоненты v 1 , v 2 , v 3 вектора скорости синовиальной жидкости зависят от переменных a _i, a 2 и a ₃, неизвестная функция давления p зависит от a _i, a ₃. Кроме того, мы имеем три неизвестные функции Q i , Q ₂, Q ₃ вектора микровращения. Толщина зазора £ зависит от компонент u i . Поэтому она может быть функцией от a _i и a ₃. Напряжения и перемещения, имеющие место в упругом слое хряща и кости и в синовиальной жидкости, создают связанные поля, представленные в системе уравнений (13)–(20), которая была получена с помощью теории упругости и механики жидкости.

• 5.    Основные уравнения и обзор решений для неньютоновской модели Даусона несжимаемой синовиальной жидкости в магнитном поле и деформируемом хряще

Проблема смазки в тазобедренном суставе человека может быть представлена с помощью системы уравнений сохранения количества движения и неразрывности для стационарного движения синовиальной жидкости в тонком зазоре и нестационарного магнитного поля с массовыми силами М . Кроме того, мы учитываем уравнения равновесия для тонкого слоя в хряще человека. Система уравнений имеет следующий вид:

div v =0,(21)

р dv/dt = Div S +M,(22)

S=-p I+npAi,(23)

GAu +(G+W3i) р mi d12,(24)

AH = pa —.(25)

5 t

Символ A i означает тензор деформации ||0 ij || , компоненты которого имеют следующий вид [14]:

е = 1 [ A _S_fv )+hL ^fLl ' ij 2 hj 5a. \k J h 5a, h, _ j j s V-1 vk d hi

^{+ 5 j} ^ОГ 5аГ^. k = i ' il'k ^a k k

Вязкость синовиальной жидкости с неньютоновскими свойствами была изучена экспериментально Д. Даусоном и В. Моу [10, 12]. Используя численные значения, полученные К. Вежхольским и С. Пытко [19, 20], была построена аппроксимационная формула для динамической вязкости в виде:

n p n , + ⁿ ° ,ⁿ” «n o ^- ( n o -n ® ^{) e} A + .... + O ( A ²⁾,             ⁽²⁷⁾

i + A • е где n® означает значение динамической вязкости синовиальной жидкости при больших скоростях скорости сдвига, no означает характеристическое значение динамической вязкости синовиальной жидкости в Пас для малых значений скорости сдвига. Символы А и В означают эмпирические коэффициенты, которые были получены из экспериментов Д. Доусона, они также зависят от индукционного магнитного поля. Коэффициенты получены численным способом и имеют значения А=1,88307 с и В=0,00458 с2 для нормального сустава человека и А=0,03349 с и В=0,00131 с2 для патологического сустава человека, если магнитное поле не возникает. Характеристическое значение скорости сдвига и функция, имеющаяся в аппроксимационной формуле (26), имеют следующий вид:

M O ^f V 0 I 0 '-^Г -                     (28)

^ s J da ₂

где e означает толщину зазора. Мы пренебрегаем членами порядка Re T , T и Т * .

После упрощений система уравнений сохранения количества движения, неразрывности и уравнения Максвелла для синовиальной жидкости в тонком зазоре и теории упругости для кости и хряща принимают следующий вид [10–14]:

0 = -1. dР । d fn dvi |+ N1 8Bi + N3

hi Sai   da2 ^ p da2 J   hi dai Изda

0=Л, da 2

2 i dhi = - i  5p  + g f^  dv3 \ Ni dB3 + N3

i hih3 da3 h3 da3 da2 ( p da2 J   hi dai h3

h ₃

d v _i da _i

+ h i ^h 3

5 v 2 ^da 2

⁽ h i v 3 ) = 0,

1 h ₁ h ₃

d f ^h 3 ^d H i 1 + _d_f h i ^d H i da _i ( h _i da _i J da 3 ( h 3 da 3

-d- G da ₂ [ da ₂

= Ц8

d ² H i d t ²

для i = 1,3,

уравнения

d da 2

( 2 G + M' u 2

^V       5a 2

d da 2

d da 2

G da 2.

( 3 K a tT * )

= 0,

где 0 < ai - ф < 2nci, 0 < ci < i, bm- nR/8 < a3 - 9 < nR/2 - bs, 0 < a2 - r < s. Для аксиально-несимметричного течения синовиальной жидкости три неизвестные компоненты v1, v2, v3 вектора скорости синовиальной жидкости зависят от переменных ai, a2 и a3, неизвестная функция давление p зависит от ai, a3, динамическая вязкость ПР синовиальной жидкости зависит от ai, a2 и a3.Толщина зазора s зависит от компонент ui вектора перемещения в хряще, поэтому она может зависеть от ai и a3. Без потери общности для компонент скорости и давления можно ввести следующие выражения:

vi = vi ⁽⁰⁾( a i, a 2 , a 3 )+ A v Y+....+ A ^k v i ⁽ⁱ⁾+ , i = i, 2, 3,

Р = Р ⁽⁰⁾( a _i, a ₂) + Ap ⁽ⁱ⁾+....+ A^kp ^(k)+...                           (37)

Символ p означает полное давление, символ p(0) означает давление для динамической вязкости синовиальной жидкости, не зависящей от скорости сдвига, а коэффициенты h1, h3 обозначают коэффициенты Ламе. Для тазобедренного сустава, рассматриваемого в сферических координатах, мы имеем hi - R sin(a3/R). Символы p(j), v(j) при j = 1, 2, 3 означают уменьшение или увеличение давления и скорости синовиальной жидкости, вызванные неньютоновскими свойствами синовиальной жидкости, у которой вязкость зависит от скорости сдвига. Для гидродинамической смазки при наличии сдавливания, накладывая классические граничные условия [29, 30, 31] на компоненту скорости синовиальной жидкости в направлении толщины зазора, мы получаем модифицированные уравнения Рейнольдса для функции гидродинамического давленияp(a1, a3) в следующей форме [13, 14]:

1 d h 1 da 1

^e 3 ⁽ u 2 ) f d p ⁽⁰⁾

П о

_v da 1

)

• —    M 1 ( t ) h 1

+ -1

^h 3 ^da 3

h 1 8 ³( u 2 ) Г d p ⁽⁰⁾

h 3 П 0

5a3 \

)

• —    M 3 ( t ) h 3

—

12 Uh 1 ,

h1 da1 f e3(u2) 5 p(1) ^ П0   da1 7 + 1 d hg da3 fh1i3 ^pl' ^ h3P0 da3 J где: 0 < a1 < 2n, 0 < a3 < Rnc3, 0 < a2 = r < e, c3 e [0,1/27],

Mt = ( N V ) Bi + 0,5 rot ( N x B ). p = p ⁽⁰⁾ + Ap ⁽¹⁾ + O ( A ²).

= 0,

В уравнениях (38) и (39) имеются неизвестные функции p ⁽¹⁾ и Ap^ 1) . Эти функции описывают изменения давления, вызванные уменьшением динамической вязкости синовиальной жидкости из-за увеличения скорости сдвига. Далее мы накладываем классическое граничное условие [23-26] на компоненты скорости синовиальной жидкости, в особенности важно это для компоненты v 2 в направлении толщины зазора при рассмотрении гидродинамической смазки, вызванной вращением кости. Из-за малых скоростей мы пренебрегаем здесь центробежными силами. Тогда мы получаем модифицированные уравнения Рейнольдса для функции гидродинамического давления p ( a i , a ₃) в форме [32]:

1 5 Г Л ^u 2 ) ^{f d} p ⁽⁰⁾

h 1 6a 1

—

П О

_v da 1

—

)

M 1 ( t ) h

± d h1 Sa1

+

1    5 ^{Г h} 1 ^e 3 ⁽ u 2 ) ^f d p ⁽⁰⁾

^h 3 ^da 3

^h 3 H o

Sa3

—

)

M 3 ( t ) h 3

= 6 го h

3 ( u 2 ) ^d p ⁽¹⁾

< ⁿ 0

1„ d

— ®^-

2 Sa 1

^{e 2(} u 2 ^{) k} 1 ^f 5 p ⁽⁰⁾

Sa _{1 7}

A"

+

1 d ^{f h} 1 ^e 3 ( u 2 ) d p ⁽¹⁾

5e ( u 2 ) 6a 1 ,

—

П ,

_v da 1

M 1 ( t ) h 1

^h 3 ^da 3 _v

—

1 _ю js 4 h 3 Sa 3

h 3 P 0    ^da 3 ₇

h 1 ² s ²⁽ u 2X1 ^f 5 p ⁽⁰⁾

П , h 3

Sa3

—

M

Yl 3 ( t ) h 3 , 7 (42)

где

p = p ⁽⁰⁾ + Ap ⁽¹⁾ + O ( A 2 ), 0 < a = ф <  2 n C 1 , 0 <  c 1 <  1, b m = n R /8 < a 3 ^ 9 < n R /2 ^ b s e = e [ u ₂( p )], — 0,02 ■ к 4[( n_w )² — П 0 П » ]( П ^ ) — 2 < — 0,04.

• 6.    Перемещения в тонкостенном хряще

Модифицированные уравнения Рейнольдса (38, 39, 41, 42) очень сильно связаны с перемещениями в кости и хряще ui , которые описываются уравнениями (14), (35), (36). Чтобы получить этих уравнений перемещения ui , мы должны сначала точно описать граничные условия. В этом случае мы используем соотношения Дюгамеля-

Неймана между компонентами Т /j- тензора напряжений S* в упругом хряще и компонентами s ij тензора деформации. Мы имеем следующие соотношения [11, 13]:

т j = 2 G s „ + ( л_Е kk - 3 а tKT * ) б j ,                      (43)

при i , j = 1, 2, 3, где: 5 ij - компоненты тензора Кронекера ( 5 ij = 1 при i = j и 5 ij = 0 при i * j ).

Далее мы рассмотрим соотношения деформация-перемещения в виде [13]:

s = 1 [ h i- -Ц". ] + h L _2_f ^u '

+ 5 Y - Uk- ^X ¹ и ^hi^hk ^да k

^j 2 И, да j I h J h да h

_ j ^j X i 7 I j X J 7

где ui - компоненты вектора перемещения u в хряще.

Мы подставляем соотношение напряжения-деформации (43) и соотношение деформация-перемещения (44) в нижеследующие уравнение движения и уравнение теплопроводности для хряща

Div S*= 0 ,                                       (45)

div (к grad Т * )=0,                                  (46)

где k - теплопроводность тела хряща, Т - температура тела хряща.

Толщина упругого слоя имеет порядок e_s, что в примерно в тысячу раз меньше радиуса кривизны тела хряща или других величин, имеющихся в области трения. Если температура T ^* в упругом хряще и вектор перемещений u в хряще не зависят от времени t и если мы пренебрегаем величинами порядка e_s, то из уравнений (45), (46) мы получаем следующую систему дифференциальных уравнений в частных производных второго порядка, а именно уравнения (34)-(36) и упрощенное уравнение теплопроводности [14]:

y^k * я ^Т " 1 = 0,                        (47)

да 2 ^ да 2 у при i = 1, 2, 3; 0 < а1 = ф < 2пc 1, 0 < c 1 <1, bm = nR/8 < а3 = 9 < nR/2 = bs.

Толщина упругого хряща изменяется в пределах от s ₂ до s 1 , то есть s ₂ < а ₂ <  s ₃. На внутренней поверхности хряща а ₂= s 2 , где упругий слой хряща контактирует с синовиальной жидкостью, нормальные напряжения равны гидростатическому давлению p с противоположным знаком, а тангенциальные напряжения равны нулю. Гидростатическое давление p действует вертикально на внешнюю поверхность упругого слоя хряща и поэтому давление не влияет на тангенциальные напряжения на поверхности. Упругий слой хряща лежит на жесткой сфере кости в положении а ₂= s 3 и поэтому контактная поверхность этих тел не деформируется давлением . Граничные условия в упругом хряще имеют следующий вид:

^T j ^{( а} 1 , ^а 2 = ^s 2 , ^а 3 ) = ^- Р ^{( а} 1 , ^а 3 ^{) 5} i 2 ⁵ j-                          ⁽⁴⁸⁾

u i ( а 1 , а ₂ = s 3 , а 3 ) = 0,                                  (49)

где i = 1, 2, 3.

Мы подставляем соотношения напряжения-деформации (43) и соотношения деформации-перемещения (44) в граничные условия (48, 49). В этих уравнениях мы пренебрегаем членами порядка s _s/R = 10 ^{- 3} в сравнении с членами порядка 1, где R означает величину радиуса головки кости. Тогда мы получаем следующее уравнение [32]:

du2           +       3аТК*АТ(а2 = R + s)-Р да2 (а1,а2 R   ,а3)           2G + Л         ,               (50)

где u ₂ = u ₂( p , T) есть компонента вектора перемещения в хряще в направлении толщины зазора и Δ T есть функция разности температуры в слое хряща в направлении толщины зазора, полученная из уравнения теплопроводности, к - есть теплопроводность тела хряща. Символ p означает полное давление. Уравнение (41) определяет неизвестное давление p ⁽⁰⁾ как первое приближение к полному давлению. Уравнение (42) определяет неизвестную функцию давления p ⁽¹⁾, то есть Аp ^lh, которая описывает коррекцию значений полного давления. Дважды интегрируя уравнение (35) относительно переменной а 2 при граничных условиях (49), (50), мы получим перемещения в упругом слое u i , где величина и ₂ означает перемещение хряща в направлении толщины зазора.

Перемещение упругого слоя в направлении толщины зазора имеет следующий вид [32]:

⁵ з                                         ⁵ з p ( _{а а} )

u 2 ^(а 1 , ^а 2 , ^а 3 ) = ^-[^а T • ~ _ , . A T * ⁽ а_ь^а 2 , ^а з ) d ^а 2 5 + [ ^J,/ d ^а 2 5 ,    ⁽⁵¹⁾

J 2 G + Л                    J 2 G + Л а2                                          а2

0 < а 1 - ф <  2 п c 1 , 0 <  c 1 <  1, b _m - n R /8 < а ₃ - 9 < n R /2 - b _s, 5 ₂ < а ₂ < a _2s <  5 ₃, a _2s есть переменная интегрирования, A T ( a 1 , a ₂, a ₃) описывает изменение температуры в упругом слое хряща.

• 7.    Общая форма зависимостей напряжения–деформации в синовиальной вязкоупругой жидкости

• 1.    Теоретическая зависимость. Вязкоупругие свойства биологических жидкостей описываются с помощью определяющих соотношений Ривлина-Эриксена [1]

S = - pI + nA1 +а( A1)2 +вА 2 + YA1A 2-(52)

Предполагаем преближенное соотношение:

A ^*

S = -pI + A1 [По + а A * + Р -4 + Y A*],

A 1

где эффективная динамическая вязкость имеет следующий вид:

np - По + aA1 + в A2 + YA2,(54)

A 1

A1 = L + LT,(55)

A2 = grad a + (grad a)T + 2LTL ,(56)

A2 - L • v + ddv •(57)

Здесь введены обозначения:

S - тензор напряжений в Па,

A ₁ - тензор скоростей деформаций в с^-1,

A ₂ - тензор скоростей деформаций второго порядка в c^-2,

L - тензор градиента скорости жидкости в с^-1,

LT - транспонированный тензор градиента скорости жидкости в с-1, p - давление, вызванное перфузией в Па, t - время в с, a - вектор ускорения в м/с2, v - вектор скорости в м/с, а - первый коэффициент, описывающий исследуемую жидкость в Па с2, в - второй коэффициент, описывающий исследуемую жидкость в Па с2,

Y = ap / n ₀ — третий коэффициент, описывающий исследуемую жидкость в Па с³,

I - единичный тензор,

П0 — динамическая вязкость в Пас2 при очень медленном движении биологической жидкости, iy динамическая вязкость в Пас2 при быстром движении биологической жидкости,

П _р эффективная вязкость биологической жидкости в Пас².

• 2.    Экспериментальная модель. Множество экспериментов, проведенных на биологических жидкостях, показывает, что динамическая вязкость уменьшается с увеличением скорости сдвига. Поэтому соотношение скорость сдвига-вязкость может быть записано в следующей форме:

П р ( A, B ) = П , + ( П о —П , )[1 + A A * + B A1A * + B A 2 ^{] — 1,}              (⁵⁸)

где коэффициент А, полученный экспериментальным путем, имеет значение от 1,200 до 2,000 с, а коэффициент В наиболее часто имеет значение от 0,00300 до 0,00600 с².

Эффективная вязкость (58) как функция двух переменных A и B может быть разложена в ряд Тейлора в окрестности точки А = 0, В = 0:

Ann                5ип п р( A, B) = n р( A = 0, B = 0) + —р- (A = 0, B = 0) A + —р (A = 0, B = 0)B + 0( A 2) + 0( B 2)

p         p               дA                 дB где n p (A = 0, B = 0) = n o,

An p д A

( A = 0, B = 0 ) = ( n o

—

⁽— A ; )

(i + a a ; + B A ; A * + B A 2 )²

A = 0, B = 0

дп„

- A^- ( A = 0, B = 0 ) A =— ( n o n , ) A A ; ,

A B ( A = 0, B = 0 ) = ( n o

—

П,)

( — a ; a ; — a 2 )

(i + a a ; + B A ; A ; + B A 2 )²

,

A = 0, B = 0

A B ( A = 0, B = 0 ) B =— ( n o —n , ) B ( A 1 A ; + A 2 )

Если подставить производные из (60) в (59), то получим:

П p ⁽ A , ^{B )} = П 0 ^{— (}П 0 ^— П , ^{) A} i A ^{0 — (}П 0 ^— П , ) A ^; A i B

^— ■| ( ⁿ 0 ^— П / ) A 2 B ^— "2 ^{( n} 0 ^— П / ^{) A} 1 B ⁺ O ( A ^{2) +} O ⁽ B ²⁾ .

Приравнивая левые и правые части соотношений (61) и (54), получим: a A ; = — ( n o - n ^ )(A + B A ; ) A ; ,

P A 2 / A ; = - ? ( n o - n » )A 2 B , Y A 2 ^ A 2 aPn 0 ^-1 = — ? ( n o - n » )A 2 B .

Обе части уравнения (62) мы делим на А ; , а обе части уравнения (63) делим на

A 2 /A ; , после чего соотношение (63) поставляем в (62). В результате получим:

a— 2 P = — ( n o —n « ) A .                              (65)

Деля обе части уравнения (64) на коэффициент A 2 , получим:

ав = -? (По-П»)По B.(66)

Решая систему алгебраических уравнений (65), (66), мы получаем значения а и в для биологической жидкости как функцию А , В , П о , П ® в виде:

а = -1 A(nо -п®)- 2 V[A(nо -n®)]2 - 4ВПо (По -П®), в = 4A(nо п,)4л![A(nо п ,)]2 -4ВПо(По - nJ.

Если 0 <<  В/A << 1 , то из решений (67),(68) получаем следующие приближенные значения:

а - -(По-n®)A +ПоВ /A+0(В2/A2), в - ? ПоВ/A+0(В2/A2),(69)

У- . - ? ( П о -П ®) В +0( В ²/ A ²).

Например, если мы предположим: п _о=10,00 Пас, n ® =0,10 Пaс, A =0,03349 с, В =0,00100 с², то из решений (69) следует, что: а = - 0,0329 Пaс², в =0,14929 Пaс², у = - 0,00495 Пaс³.

Если, следуя Астарита и Маруччи [1], принять, что а>0, в<0, у<0,то из уравнений а-2в= -(По-П®)A, ав=-? (По-П®)ПоВ(70)

получим:

а = -2A(nо п, h 2V[A(nо п,)]2 + 4Bnо(nо -n®), в = -2A(nо п,) 4д([A(nо п,)]2 + 4Bnо(nо -n®).

Если 0 <<  В / A << 1 , то из решений (71), (72) следуют следующие приближенные хзначения:

а - +ПоВ/A+0(В2/A2), в - -(По-П»)A - ? ПоВ/A+0(В2/A2),(73)

Y- . - ? ( П 0 -П ®) В +0( В ²/ A ²).

Например, если мы предположим, что n 0 = 10,00 Пaс, n ® = 0,10 Пaс, A = 0,03349 с, В = 0,00100 с², то из решений (73) мы получим следующие величины: а = 0,2985 Пaс², в = -0,312 Пaс², у = - 0,00495 Пaс³. Здесь неравенство а < -2 в из [1] удовлетворяется. Этот факт подтверждает наличие нормальных напряжений в вязкоупругой неньютоновской синовиальной жидкости [1].

• 8.    Деформированная толщина зазора в тазобедренном суставе человека

Для тонкого слоя, лежащего на сферической поверхности кости, мы имеем следующие коэффициенты Ламе:

h 1 = R 81н( а 3 / R ), h 2 =1, h 3 =1,                               (74)

где R - радиус сферы. Далее введем обозначения: а 1 = ф - окружное направление, а ₂ =r - направление толщины зазора, а ₃ П - меридиональное направление. Зависимости между прямоугольными ( x , y , z ) и сферическими ( а 1 = ф , а ₂= r , а ₃= 9 ) координатами имеют классический вид:

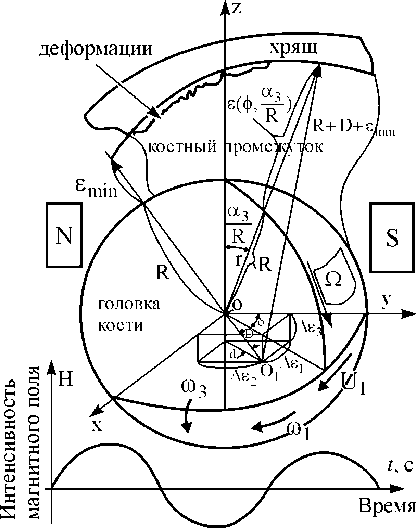
Рис. 5. Центры сферического тела хряща и сферической головки кости при смазке, вызванной вращением при переменном времени, в зависимости от интенсивности магнитного поля H и деформации хряща

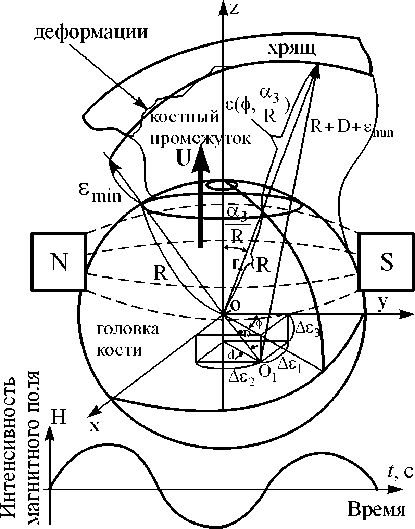
Рис. 6. Центры сферического тела хряща и сферической головки кости при смазке, вызванной сдавливанием

Рис. 7. Область распределения давления, покоящаяся на поверхности головки кости, при смазке, вызванной вращением

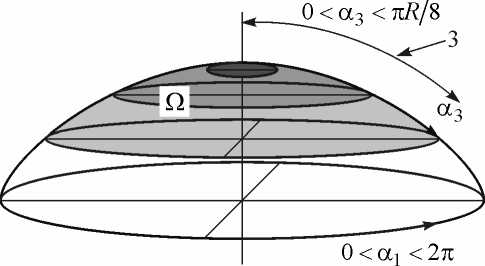
Рис. 8. Область распределения давления, покоящаяся на поверхности головки кости, при смазке, вызванной сдавливанием

x = r sin( — ) CОS ф , y=r sin(— ) sin ф , z = r cos( —), 0 < r < R . RRR

Графическая иллюстрация центра сферической головки кости O (0, 0, 0) и центра сферического хряща в точке O 1 ( x - Аец у - Ае ₂, z + Ае ) для гидродинамической смазки, вызванной вращением, представлена на рис. 5; для гидродинамической смазки, вызванной сдавливанием, - на рис. 6. Область гидродинамической смазки, обусловленой вращением, показана на рис. 7, вследствие сдавливания - на рис. 8.

Уравнение сферической поверхности хряща в центральной точке O 1 ( x - Ае 1 , у - Ае ₂, z + Ае ) может быть переписано в следующей форме:

( x - Ae i )²+ (у - Ае 2 )²+ ( Z + Ае з )²=( R + D + е min )², D =[ ( Ае 1 )²+( Ае 2 )²+( Ае з )²].^0,5      (76)

После подстановки соотношений (75) в (76) получим:

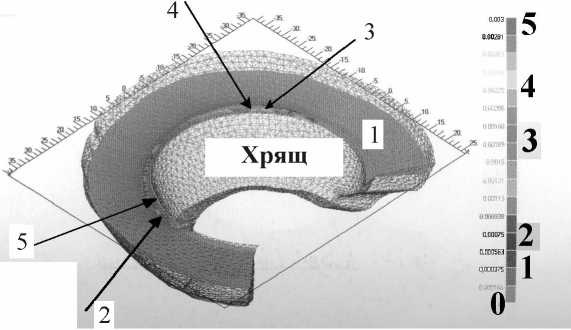
Рис. 9. Экспериментальные данные о деформации поверхности суставной чашечки в тазобедренном суставе человека (приводится по [15])

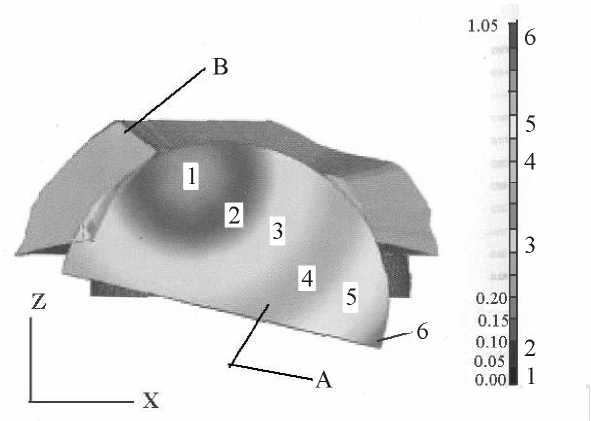
Рис. 10. Экспериментальные данные о поверхности головки кости в тазобедренном суставе человека (приводится по [15])

( r cos ф sin a ₃/ R - А£ 1 )²+( r sin ф sin a ₃/ R - А£ ₂)²+( r cos a ₃/ R + А£ ₃)²=( R + D + £ _min)².    (77)

Выражение для толщины зазора имеет следующий вид:

£ ( Ф , а 3 R) u2+ r-R.                               (78)

Здесь величина r может быть найдена из (77) и подставлена в (78). Поэтому формула для толщины зазора окончательно имеет следующий вид:

£ ( ф , а ₃/ R )= и ₂+ А£ ₁cos ф sin( a ₃/ R )+ А£ ₂ sin ф sin( a ₃/ R )- А£ ₃ cos( a ₃/ R ) - R +

+ {[ А£ ₁cos ф sin( a ₃/ R )+ А£ ₂ sin ф sin( a ₃/ R )- А£ ₃ cos( a ₃/ R )]²+( R + £ _min)( R +2 D + £ _min)}^0,5. (79)

Экспериментальные значения деформации кости и поверхности суставной чашечки в тазобедренном суставе человека, полученные в работе [15], сравнены со значениями, полученными в данной работе с помощью упрощенных уравнений теории упругости (34)-(36) при граничных условиях (50). Различия между этими результатами составляют около 10 процентов. Экспериментальные значения деформации поверхности чашечки в тазобедренном суставе человека по данным работы [15] составляют от 8 до 30 мк в нагруженной зоне (рис. 9). Экспериментальные значения деформации поверхности головки кости в тазобедренном суставе человека локализованы в основном в нагруженной зоне и имеют значения от 5 до 10 мк (рис. 10).

Эти деформации получены с помощью метода компьютерной томографии, с использованием аппаратуры, описанной в [15]. Вышеуказанные значения деформаций введены в уравнения количества движения и в модифицированные уравнения Рейнольдса и использованы в дальнейших численных расчетах.

Минимальное значение толщины зазора в сферическом тазобедренном суставе мы находим из формулы [8]:

₂      0,6                                           _{2            2}

^ min _ ^2 П 5 0,4 [^ | , 5 _ C^,- = ¹ 1 1^- + 1 -^ 2 R          ¹ ( C J ¹ ER ² E 2 ( E 1 E ₂ J

где E 1 , E ₂, v i , v ₂ - упругие модули и коэффициенты Пуассона для головки кости и хряща, соответственно, С - нагрузка, а величины n , to , R были определены ранее. Зависимость (27) для 0«ro R /£ _min может быть написана в следующей форме:

го R ²n _ 5 ₂

C " 5 1

'• n, ,     По          о    toRno no +1 + 53 — ’ 52 _ ER '

I            E min J

5 3 _ A to.

Комбинируя уравнения (80) и (81), мы получаем систему двух уравнений для определения двух неизвестных величин, а именно динамической вязкости n синовиальной жидкости и минимального значения £ _min толщины зазора, где учтены упругие деформации хряща. Если предположить следующие данные: R =2,6 х 10^-2 м, E =2 х 10⁵ Па, to R =3 х 10^-1 м/с, n » =0,10 Пас, 2 п R / C =3 х 10^-4 м/Н, пп» - 1000, A =1,88 с, C =544,26 Н, то из уравнений (99), (100) мы получаем: Sm_m =0,0000208 м=20,88 мк и n =0,1036 Пас. Если взять для вычислений следующие величины: : A =1,88 с, П о =100,00 Пас, n ® =0,10 Пас, R =0,020 м, C =544 Н, 0,50 с^-1 <го< 10,00 с^-1, 2 х 10⁵ Пa < E < 2 х 10⁷ Па,то мы получаем минимальное значение толщины зазора в диапазоне: 0,29 мк <£ _min < 19,90 мк.

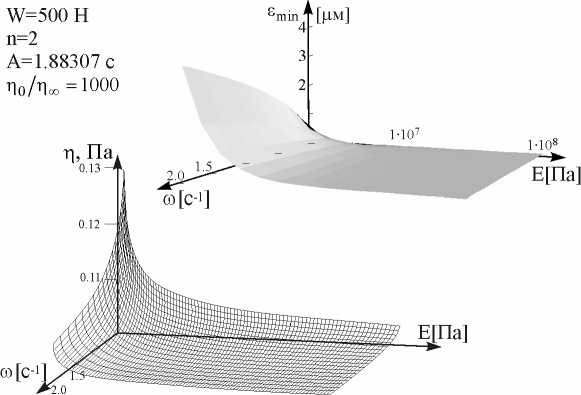
Рис. 11. Зависимость минимальной толщины зазора сустава и динамической вязкости синовиальной жидкости от упругого модуля хряща и скорости сдвига жидкости

С помощью вышеуказанных вычислений мы можем показать зависимости между минимальным значением толщины зазора s _min, упругим модулем хряща E и скоростью сдвига синовиальной жидкости (рис. 11). Если упругий модуль хряща убывает, то увеличивается деформация хряща и увеличивается минимальное значение толщины зазора. Динамическая вязкость синовиальной жидкости зависит от упругого модуля хряща (рис. 11).

Чтобы объяснить этот факт, мы можем заметить, что если упругий модуль хряща уменьшается, то прочность хряща также уменьшается, а минимальная величина зазора сустава увеличивается, и потому уменьшается скорость синовиальной жидкости, также уменьшается скорость сдвига течения и увеличивается вязкость синовиальной жидкости.

• 9.    Численные вычисления распределения давления и несущей способности в деформированном сферическом тазобедренном суставе человека

  • 9.1.    Распределение давления и несущая способность

Общую несущую способность на криволинейной головке кости можно получить с помощью поверхностного интеграла по следующей формуле:

C общ = JJ Р ^{( а} 1 , ^а 3 ) d ^Q ( ^a 1 , ^а 3 )•                           ⁽⁸²⁾

Q^ , а з )

Элемент площади в двойном интеграле имеет следующий вид:

d Q =

^{5 r}0 /Х

5ф 59

d ф d 9 .

Символ r ₀ означает радиус-вектор для поверхности головки кости и 0< a i ф <2 п c 1 , 0< c 1 <1, п R 8< a ₃ 9 < п R /2 для вращения и 0< a ₃ 9 < п R /18 для выдавливания. Радиус-вектор r ₀ можно получить по формуле:

r0=i x + j y + k z,(84)

где i , j , k - единичные векторы и для сферических координат мы имеем:

x=R cos ф sin9/R, y = R sin ф sin9/R, z= R cos9/R.(85)

Если мы вставим формулу (85) в (84), а затем (84) в (83), то получим:

dQR2 sin(9/R)dфd(9/R)•(86)

• 9.2.    Распределение давления при наличии гидростатической смазки при вращении

Если магнитным полем можно пренебречь, то модифицированное уравнение Рейнольдса (41) для гидродинамической смазки при вращении сферической головки кости имеет следующий вид:

' u ' ⁵Р 1

5ф( n _o 5ф ,

+ R ² si

9P

R J 59

£ ³ ( u ₂ ) 5 p^(o ) ."чТ 59

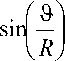
₂ 5s( u ₂) . / 91 = 6 w R ---—sin I — I

5ф ( R J ,

где 0,30 n < a _l ф <1,30 п , п R /8< а ₃ =9 < п R /2.

Численные вычисления были проведены с использованием метода конечных разностей при помощи вычислительной программы Маткад 2000. При вычислениях мы принимали следующие значения параметров для зазора сустава: Δε1=2 мк, Δε2= 2 мк, Δε3=+2 мк, радиус головки кости R=0,026575 м и атмосферное давление на границе области Ω(α1,α3), покоящейся на головке кости (рис. 6). Для нормального тазобедренного сустава мы берем в вычислениях наименьшую толщину зазора εmin=2,0 мк. Учитывая угловую скорость головки кости ω=1 с-1 и среднее значение динамической вязкости синовиальной жидкости η0=0,03 Пас, мы получим из уравнения (87), что гидродинамическое давление p(0) имеет максимальное значение, равное 1,11 ×106 Н/м2 и несущую способность Cобщ=673 Н. Учитывая угловую скорость головки кости ω=0,1s-1 и среднее значение динамической вязкости синовиальной жидкости ηo=0,40 Пaс, мы получаем из уравнения (87), что гидродинамическое давление p(o) имеет максимальное значение, равное 1,44 ×106 Н/м2 и несущую способность Cобщ=897 Н (рис. 12). Поверхность смазки имеет площадь πR2cosπ/8≈20,50 см2.

Для патологического тазобедренного сустава мы берем в вычислениях наименьшую толщину зазора ε min =1,0 мк. При угловой скорости головки кости ω =1 с^-1 и средней величине динамической вязкости синовиальной жидкости η o =0,005 Пас мы получим из уравнения (87), что гидростатическое давление p ^(o) имеет максимальное значение, равное 0,76 × 10⁶ Н/м², и несущая способность равна C общ =341 Н. Принимая значения ω =0,1 с^-1 и η o =0,07 Пaс, мы получаем из уравнения (87), что гидростатическое давление p ^(o) имеет максимальное значение, равное 1,034 × 10⁶ Н/м², и несущую способность C общ =477,5 Н. Полученные распределения давления на головке кости для нормального и патологического зазора тазобедренного сустава человека показаны на рис. 12, 13.

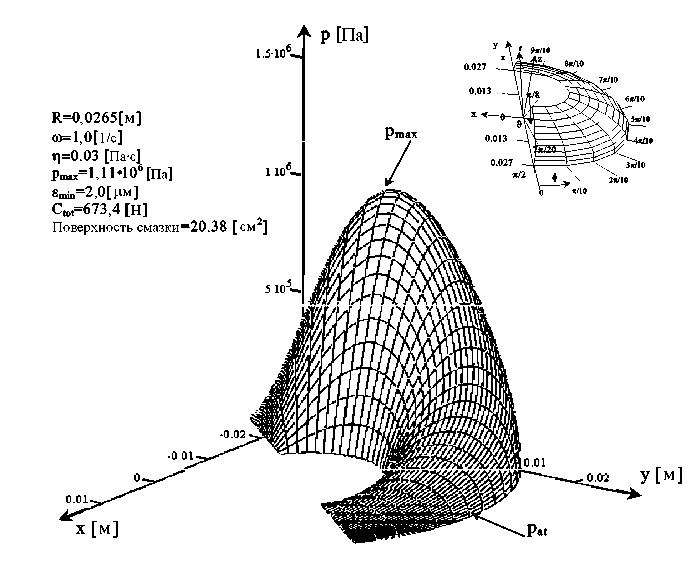
Рис. 12. Два случая распределения давления в нормальном сферическом тазобедренном суставе человека при гидродинамической смазке, вызванной вращением

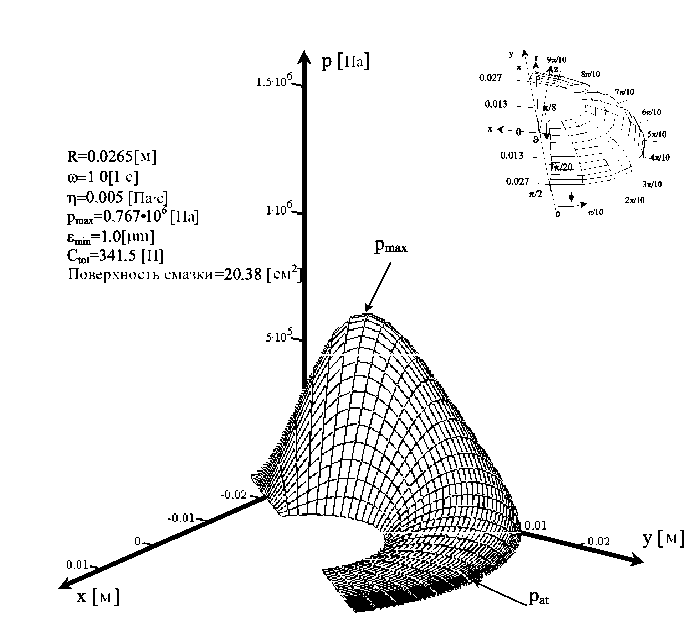
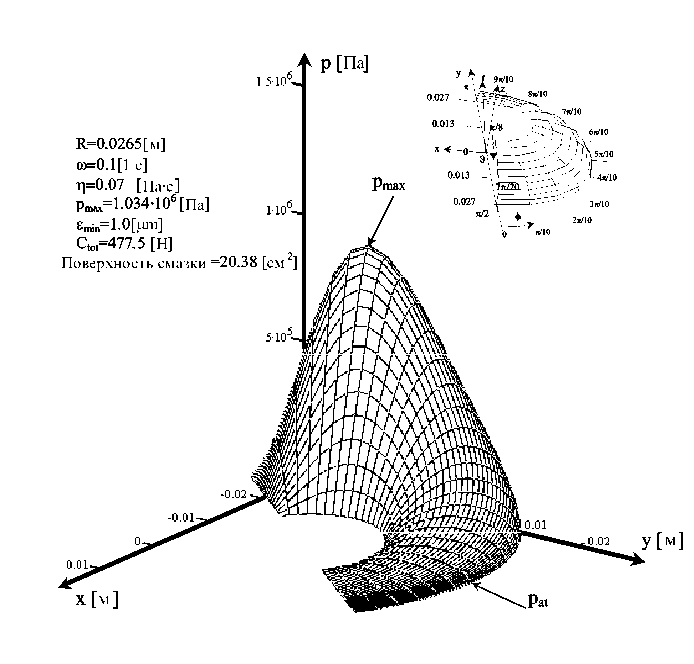
Рис. 13. Два случая распределения давления в патологическом сферическом тазобедренном суставе человека при гидродинамической смазке, вызванной вращением

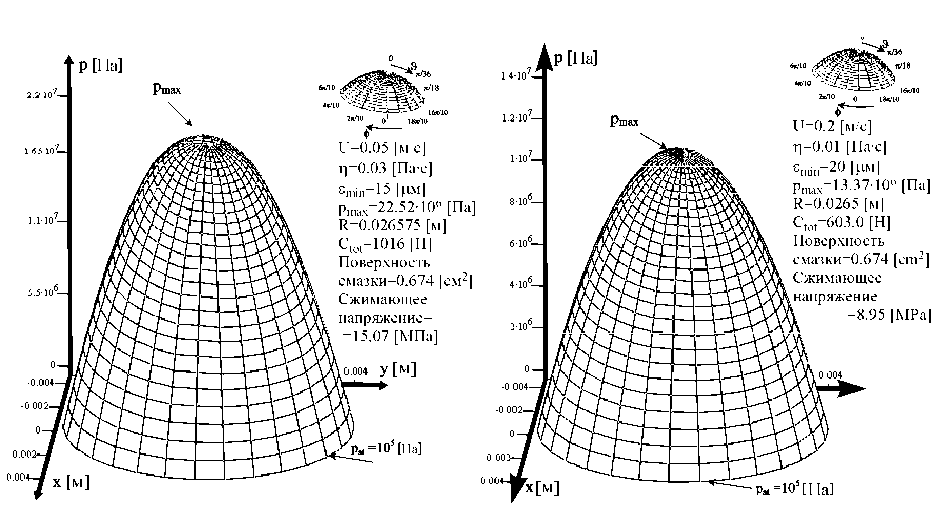
Рис. 14. Два случая распределения давления в нормальном сферическом тазобедренном суставе человека при гидродинамической смазке, вызванной cдавливанием

Для несущих способностей 897 Н, 673 Н, имеющих место в нормальном суставе, мы получаем следующие сжимающие напряжения: σ =897 Н/20,4 см² =0,43 Н/мм²=0,43 MН/м² и σ =673 Н/20,4 см²=0,33 Н/мм²=0,33 MН/м². В патологическом суставе сжимающие напряжения равны: σ =341 Н/20,4 см²=0,16 Н/мм²=0,16 MН/м² и σ =477,5 Н/20,4 см²=0,23 Н/мм²=0,23 MН/м². Эти напряжения меньше, чем прочность при сжатии 21 MН/м² для кости человека [2, 6, 7, 8, 9].

• 9.3.    Гидродинамическая смазка при сдавливании

Если магнитным полем можно пренебречь, то уравнение Рейнольдса (38) для гидродинамической смазки, вызванной выдавливанием между сферическими головками сустава, имеет вид:

• ^{1     ∂} ( ^{ε ∂ρ} ) + ^∂ ( R sin( ^ϑ ) ^{ε ∂ρ} ) =- 12 UR sin ^ϑ ,

  
  

_{R sin} ϑ ∂ϕ η ₀ ∂ϕ ∂ϑ R η ₀ ∂ϑ             R

R

0< а 1 ф<2п, 0< а₃ S< R п /18, 0< а₂ = г <г .

В вычислениях взяты следующие параметры для зазора сустава человека: Δε 1 =–5 мк, Δε 2 =–5 мк, Δε 3 =+5 мк, радиус головки кости R =0,026575 м и атмосферное давление на границе области Q ( a _l, a ; ):{0< a_l ф<2п, 0< a₃ ^< R п /18}, покоящейся на головке кости (рис. 7). Принимая однородную скорость головки кости U =0,05 м/с, наименьшую толщину зазора ε min =15 мк и среднее значение динамической вязкости синовиальной жидкости η o =0,03 Пас, мы получаем из уравнения (88), что гидродинамическое давление p ^(o) имеет максимальное значение, равное 22,52 × 10⁶ Н/м², несущую способность C общ =1016 Н. Беря однородную скорость головки кости U =0,20 мс^-1, наименьшую толщину зазора ε min =20 мк и среднее значение динамической вязкости синовиальной жидкости η o =0,01 Пас, мы получаем из уравнения (88), что гидродинамическое давление p ^(o) имеет максимальное значение, равное 13,37 × 10⁶ Н/м².

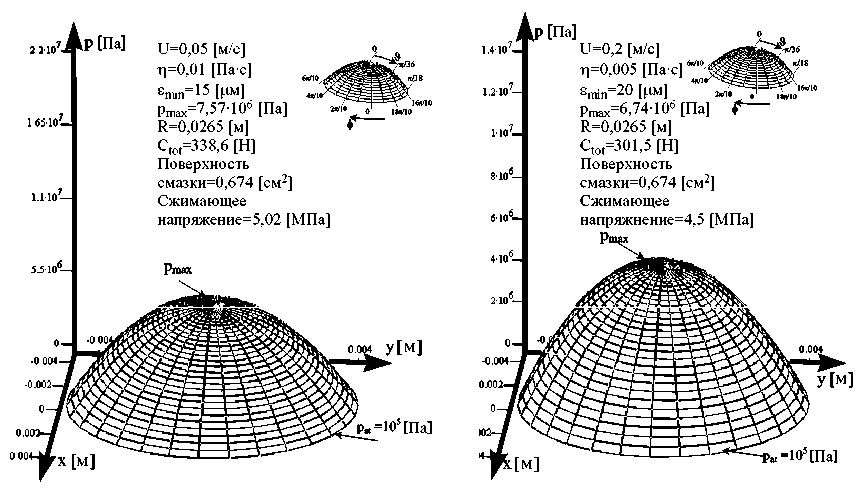
Рис. 15. Два случая распределения давления в патологическом сферическом тазобедренном суставе человека при гидродинамической смазке, вызванной cдавливанием

Площадь поверхности смазки имеет значение 2 π R ²[1-cos( π /18)] ≈ 0,67 см² и несущую способность C общ =603 Н (рис. 14).

Для патологического тазобедренного сустава мы принимаем в вычислениях однородную скорость головки кости U =0,05 мс^-1, наименьшую толщину зазора ε min =15 мк и среднее значение динамической вязкости синовиальной жидкости η o =0,01 Пас. Тогда мы получаем из уравнения (88), что гидродинамическое давление p ^(o) имеет максимальное значение, равное 7,57 × 10⁶ Н/м², и несущую способность C общ =338,6 Н. Принимая однородную скорость головки кости U =0,20 с^-1 , наименьшую толщину зазора ε min =20 мк и среднее значение динамической вязкости синовиальной жидкости η o =0,005 Рас, мы получим из уравнения (88), что динамическое давление p ^(o) имеет максимальное значение, равное 6,74 × 10⁶ Н/м². Площадь контактной поверхности имеет значение ≈ 0,674 см² и несущая способность C общ =301,5 Н (рис. 15).

Для несущих способностей 1016 Н и 603 Н, имеющих место в нормальном суставе, мы получаем следующие сжимающие напряжения: σ =1016 Н/0,674 см²=15,07 Н/мм²=15,07 MН/м² и σ =603 Н/0,674 см²=8,95 Н/мм²=8,95 MН/м². В патологическом суставе сжимающие напряжения имеют следующие значения: σ =338,6 Н/0,674 см²=5,02 Н/мм²=5,02 MПа и σ =301,5 Н/0,674 см²=4,5 Н/мм²=4,5 MПа. Эти напряжения меньше, чем предельные напряжения при сжатии, равные 21 MН/м² у здорового человека в возрасте 20-30 лет. Предельные напряжения при сжатии у 70 -летнего человека имеют значения около 12 MН/м². Большие напряжения приведут к разрушению сустава [2, 79].

Представленный метод позволяет получить решение в форме ряда Тейлора по степеням малого параметра А. Этот параметр был получен экспериментально для синовиальной жидкости. В частном случае для симметричного течения можно найти с помощью представленной теории аналитические решения в простой форме. Процентные поправки скорости v i ⁽¹⁾ и давления p ⁽¹⁾ , вызванные неньютоновскими свойствами синовиальной жидкости, оцениваются численно по следующему отношению:

Ap ⁽¹⁾ + O ( A ²)

_p (0)

⋅ 100%.

Для больших скоростей сдвига: 100 с^-1 ≤Θ≤ 1000 с^-1 вязкость синовиальной жидкости мала и имеет значения 10^-2 Пас ≤η≤ 10^-1 Пас (рис. 4a) . В этом случае из уравнения (89) мы получаем малые изменения давления от 2% до 4%. Для малых скоростей сдвига : 10^-1 с^-1 ≤Θ≤ 10 с^-1 вязкость велика 10 Пас ≤η≤ 100 Пас . В этом случае из уравнения (89) мы получаем изменения давления от 7% до 15%. Нестационарное индукционное магнитное поле 0,1 мT с частотой около 60 Гц изменяет давление на 1– 4%.

Благодарность

Автор благодарен за финансовую поддержку (грант KBN 8–T 11E–021–17,

Польша).