Распределение энергии отработавших газов между элементами системы "газовая турбина - эжектор - охладитель наддувочного воздуха" в дизеле с наддувом

Энергия отработавших газов (ОГ) в дизеле с газотурбинным наддувом и промежуточным охлаждением наддувочного воздуха (НВ) в зависимости от их температуры, давления и расхода может быть условно подразделена на высоко- и низкопотенциальные составляющие. Энергию

ОГ на выходе из выпускного коллектора относят к высокопотенциальной, а энергию ОГ после срабатывания части ее в турбине турбокомпрессора – к низкопотенциальной составляющей.

Низкопотенциальная составляющая энергии ОГ характеризуется пониженными давлением и температурой и, как правило, расходуется либо на удаление пылевых частиц из пылесборников воздушных фильтров, либо на осуществление циркуляции атмосферного воздуха через матрицы радиаторов системы охлаждения или охладителей наддувочного воздуха посредством эжектиро-вания, либо выбрасывается в атмосферу, загрязняя окружающую среду. В связи с последним важно уменьшать энергию, теряемую в результате такого выброса ОГ.

Поэтому целесообразно полнее использовать низкопотенциальную составляющую энергии ОГ, например, для снижения затрат на осуществление циркуляции атмосферного воздуха через матрицы охладителей наддувочного воздуха (ОНВ) посредством эжектирования. С этой целью необходимо дальнейшее совершенствование эжекционных систем охлаждения наддувочного воздуха путем рационального распределения энергии между элементами этой системы, к которым относятся газовая турбина, эжектор и охладитель наддувочного воздуха (рис. 1).

При применении эжектора для циркуляции охлаждающего воздуха (ОВ) из атмосферы через ОНВ, рабочим потоком в котором являются отработавшие газы, нагретый наддувочный воздух после компрессора 4 под определенным давлением и с соответствующей температурой направляется в ОНВ 2. В ОНВ происходит теплообмен между наддувочным воздухом после компрессора и охлаждающим воздухом из атмосферы, после чего НВ направляется в цилиндр дизеля. Отработавшие газы из цилиндра дизеля поступают в турбину 5 турбокомпрессора, в которой срабатывается часть энергии для привода компрессора 4. После турбины отработавшие газы поступают в эжектор 8, где, расширяясь в сопле, передают оставшуюся часть кинетической энергии охлаждающему воздуху, увлекая и осуществляя его циркуляцию через ОНВ [1, 2].

Материалы и методы

Известно, что элементы системы эжекционного охлаждения служат для повышения плотности наддувочного воздуха: турбина – посредством увеличения работы компрессора и, как следствие, повышения давления р _к наддува, а эжектор – посредством снижения температуры T_k наддувочного воздуха за счет обеспечения необходимого циркуляционного расхода G ов охлаждающего воздуха.

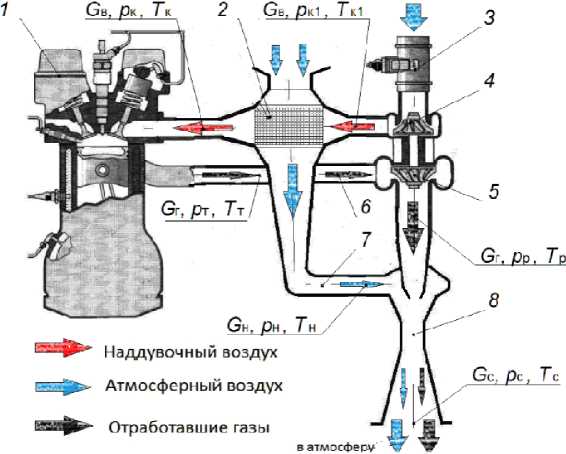
Рис. 1. Структурная схема эжекционной системы охлаждения НВ и параметры газовоздушных потоков в сечениях ее элементов: 1 – дизель, 2 – ОНВ, 3 – устройство измерения расхода воздуха, 4 – компрессор, 5 – турбина, 6 – трубопровод ОГ, 7 – трубопровод ОВ, 8 – эжектор

Fig. 1. Block diagram of the HB ejection cooling system and parameters of gas-air flows in the sections of its elements: 1 – diesel, 2 – ONV, 3 – air flow measurement device, 4 – compressor, 5 – turbine, 6 – exhaust gas pipeline, 7 – OV pipeline, 8 – ejector

Для обеспечения требуемой эффективности эжекционной системы необходимо принятие компромиссных решений по рациональному распределению энергии между элементами этой системы, при котором обеспечивается максимальная плотность наддувочного воздуха при минимальных затратах энергии на циркуляцию охлаждающего воздуха через матрицу охладителя по сравнению, например, с вентиляторной системой охлаждения. Возможность достижения максимальной мощности дизеля при использовании эжектора для циркуляции охлаждающего воздуха через матрицу ОНВ требует дополнительного рассмотрения.

Для обеспечения требуемой степени ΔТ охлаждения НВ необходим анализ параметров и режимов работы элементов эжекционной системы с оценкой ее эффективности при углубленном рассмотрении. В настоящей статье эффективность системы «турбина - эжектор - охладитель наддувочного воздуха» оценивалась на примере системы газообмена в дизеле 4ЧН13/15.

Для оценки эффективности системы «турбина - эжектор - охладитель наддувочного воздуха» определялись соответствующие критерии и условия их использования. С этой целью рассмотрим адиабатную работу компрессора, представленную в работах [3, 4]:

Н к = П к П т Н т , (1)

где п к , П т - КПД компрессора и турбины соответственно; Н т - адиабатная работа турбины турбокомпрессора.

Расчетный анализ проводится обычно применительно к номинальному режиму работы дизеля, при этом значения КПД компрессора и турбины примем неизменными.

Степень повышения давления п к наддувочного воздуха в компрессоре можно определить, следуя рекомендациям работ [5, 6]:

^П к

H k

k в - 1   1    ₊₁^ k в^- 1

k в   R в Т 0    )

где k в , R _в - показатель адиабаты и газовая постоянная воздуха соответственно; Т 0 - температура окружающей среды.

Считая процесс сжатия адиабатным, можно принять, что температура Т ji наддувочного воздуха после компрессора определится в соответствии с работами [7, 8]:

^k в ^{- 1}

T k 1 = T o п _к ^{к в} .                                                                                                     (2)

Плотность наддувочного воздуха после компрессора в таком случае составляет pk         kв

^P к 1 = _D     = ^р 0 ^п к ^,

R _в T _k1

где р о - плотность воздуха перед компрессором; p _k - давление наддувочного воздуха после компрессора.

Коэффициент эжекции и может быть найден из уравнения, приведенного в работе [9]:

u ln PcL = п _э ln п _э =п _э ln ^{П п}- ,                                                                         (4)

Рн                  Пт где   пэ - КПД эжектора; p с, p н - давление охлаждающего воздуха после и перед эжектором со ответственно; пп, пт, пэ - степени понижения давления соответственно в системе «турбина -эжектор», турбине и эжекторе.

Давление р н можно представить, согласно работе [10], в виде п п Е Pов wH p н = p о —4,                                                                         (5)

где £ - коэффициент гидравлического сопротивления ОНВ; р _ов - средняя плотность охлаждающего воздуха; w _н - средняя скорость движения охлаждающего воздуха через матрицу ОНВ.

При неизменной площади канала F w матрицы ОНВ скорость w потока зависит от расхода G _ов и плотности ρ ов , а расход G ов , в свою очередь, зависит, в соответствии с рекомендациями работ [11, 12], от коэффициента эжекции и и расхода воздуха дизелем G _в:

w = GIT = GF = f ( u , ^Тк1 ) .                                                 (6)

P ов ^Fw   ^p ов F w

При G _в<<  G _ов пренебрежение изменением плотности дает малую погрешность, и для простоты рассуждений можно записать:

Р н = Au 2 ,                                                                                        ⁽⁷⁾

где А - некая постоянная величина.

Температура наддувочного воздуха перед впускными клапанами дизеля, согласно работам [13, 14], определится

Т К = Т К1 -А Т .                                                                              (8)

Таким образом, плотность наддувочного воздуха после ОНВ определится, в соответствии с работами [15, 16], в виде

Рк= — =     'рк--- ;,                                                                 (9)

^к   R e T k    R ( T ei -а т )

где pк = p0 пк - давление наддувочного воздуха после ОНВ; Tk - температура наддувочного воз- духа после ОНВ; ΔTk – понижение температуры наддувочного воздуха в ОНВ.

Так как Δ Т = f(u), а u = f(π т ), то и Т к = f(π т ). Это означает, что плотность наддувочного воздуха после ОНВ есть функция лишь степени понижения π _т давления в турбине .

При нахождении оптимального значения степени понижения давления в турбине можно ис- ходить из условий, определяемых результатами решения приведенных ниже уравнений:

• 1)    определения максимальной степени охлаждения наддувочного воздуха

(— I = о ;

[ дпт )

^{т Уп} п

• 2)    достижения максимальной плотности наддувочного воздуха

  ^дР, дп.

  
  

  - I = о ;

  
  

  '^т ■ T , Р т

  
  

• 3)    получения максимальной мощности дизеля с газотурбинным наддувом [^ 1   = 0 .

I дпт L т Tт, pт

В силу сложности решение представленных уравнений целесообразно в численном виде. Таким образом, определение параметров эжекционного устройства в рассматриваемой системе охлаждения наддувочного воздуха в общем виде сводится к нахождению компромиссного распределения энергии отработавших газов между турбиной и эжектором.

Результаты и обсуждение

Особенности распределения энергии отработавших газов в эжекционной системе охлаждения между газовой турбиной и эжектором заключаются в существовании максимального снижения температуры наддувочного воздуха Δ Т max , исходя из выражения (10), что становится очевидным при анализе двух предельных случаев распределении энергии отработавших газов:

• –    энергия отработавших газов (теплоперепад Н _п) полностью срабатывается в турбине. При этом эжекционное устройство не функционирует, т. е. коэффициент эжекции u = 0, что означает отсутствие циркуляции охлаждающего воздуха через ОНВ и снижение температуры наддувочного воздуха Δ Т близко к нулю;

• –    энергия отработавших газов (теплоперепад Н _п) полностью срабатывается в эжекционном устройстве, работа турбины и, соответственно, компрессора равна нулю. В этом случае разность

температур охлаждающего и наддувочного воздуха практически отсутствует и, несмотря на наличие циркуляции охлаждающего воздуха через ОНВ, снижение температуры наддувочного воздуха Δ Т также близко к нулю.

Поскольку функция Δ Т = f ( π т ) в рассматриваемом интервале изменения степени понижения давления в турбине непрерывна и дифференцируема, она имеет экстремум в соответствии с теоремой Ролля.

• О    плотности наддувочного воздуха сказать подобное нельзя. Рассмотрим уравнение (9) и найдем необходимое условие существования экстремума для плотности воздуха после ОНВ как функции от π т :

• * ( 4 ,-А T ) - p _k [ T - d^

  ^ = 0 .                                                    (13)

  
  

d рк _d п, K1 J ^ d пт d пт dпт Rв (Td -АT )2

После элементарных преобразований уравнение можно привести к следующему виду:

d П к It 1 at. d ^Л T

p0 ~—I Tk  --Л T + Пк ~— I = 0, d Пт ^   kв           d nk J откуда следует два условия:

d ⁿ^ = 0    и   T^ — — Л T + п _к d ^Л T = 0 .

d пт                k„           d nk т   вk

Для рассмотрения первого условия уравнение (2) представим в виде

П _к = 1 + вт 1

—

к _т — ¹ У 1 l

kв kв —1

^П т

,

где p = —--в—— - параметр, характеризующий различие теплофизических свойств ОГ и ОВ;

^к т   ^к в   ¹ R E

^Т = П гтн

1 +

1  ] Л

« L Ф пр J Т 0

– параметр, характеризующий нагрузку дизеля; η гтн – КПД турбокомпрес-

сора; α – коэффициент избытка воздуха; ϕ пр – коэффициент продувки; L 0 – теоретически необходимая масса воздуха для полного сгорания 1 кг топлива.

В итоге получим решение следующего вида:

к _т — 1

пУ = .                                                                  (16)

1+ вт

Однако это математическое решение не может быть реализовано физически. Несмотря на то, что τ – функция от π _т, она так же, как и β , величина положительная и всегда больше единицы, а это означает, что в выражении (16) значение π т должно быть меньше единицы, чего, очевидно, не может быть.

Для рассмотрения второго условия выполним преобразования и получим d Л T  Л T   ^1  —Г

в

= ' ^к| I ^П к    .

• ^{d П} к    ^П к         ^к в

Решение этого обычного линейного уравнения первого порядка представляется, согласно рекомендациям работ [17, 18], в виде кв —1

Л T = T 0 П к ^{к в} + С П к = T k1 + С П к .                                                             (18)

Если константу С определить, исходя из параметров номинального режима работы дизеля с вентиляторной системой охлаждения наддувочного воздуха, то для сохранения равенства потребуется увеличение Δ Т . Другими словами, рассматривая охлаждение наддувочного воздуха как средство повышения его плотности, при установке эжектора сохранение плотности, достигаемой при использовании вентилятора для циркуляции охлаждающего воздуха, обеспечивается большим значением степени охлаждения Δ Т . Это объясняется тем, что несмотря на уменьшение температуры Т к1 при снижении р к , сохранение исходного уровня Δ Т будет недостаточно, поскольку установка за турбиной эжекционного устройства влечет за собой снижение π т , а следовательно, в итоге уменьшение давления р к и плотности ρ к , создаваемых компрессором.

При отсутствии охлаждения наддувочного воздуха плотность как функция от π _т меняется в соответствии с зависимостью (3). Температура Т к1 растет в меньшей степени, чем π k , и прирост плотности наддувочного воздуха от увеличения его давления выше (рис. 2). На рис. 2 представлены: относительная степень повышения давления наддувочного воздуха зависимостью

• 1    d n                                                                   1 dT_k

пк =--к , относительная температура наддувочного воздуха зависимостью Tk =--— и пк d пт                                                                          T^ d Пт с                                                           '  dР быстрота изменения плотности наддувочного воздуха зависимостью р = —— .

dnт

Можно заметить, что при отсутствии охлаждения наддувочного воздуха в ОНВ его плот- ность возрастает при увеличении пт, так как температура Тк растет медленнее, чем пк. Появление экстремума функции АТ=f пт) объясняется ситуацией, когда увеличение температуры наддувочного воздуха в какой-то момент начнет превышать рост его давления (рис. 3).

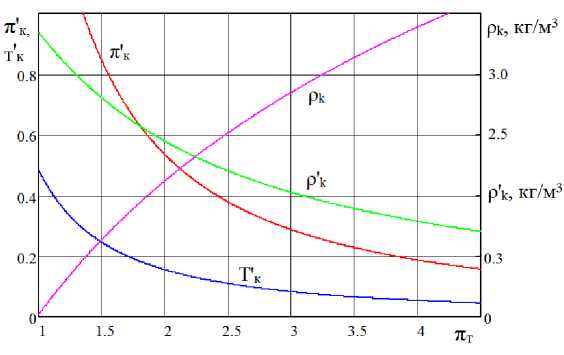
Рис. 2. Изменение относительных степени повышения давления, температуры, плотности ρ к и быстроты изменения плотности наддувочного воздуха в зависимости от π т

Fig. 2. Changes in the relative degree of increase in pressure, temperature, and density of the ρ k and the speed of change in the charge air density depending on the π т

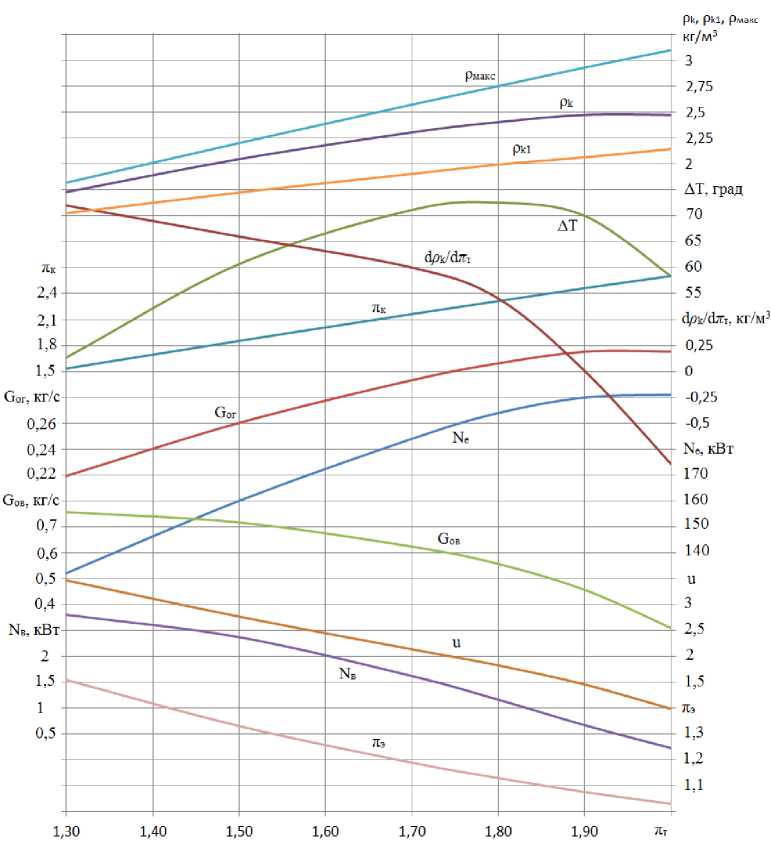
Рис. 3. Параметры турбокомпрессора и элементов системы «газовая турбина – эжектор – охладитель наддувочного воздуха» в зависимости от π т

Fig. 3. Parameters of the turbocharger and elements of the “gas turbine – ejector – charge air cooler” system depending on the π т

Увеличение мощности дизеля в соответствии с уравнением (12) обусловлено снижением ее затрат на циркуляцию охлаждающего воздуха, осуществляемую эжекционным устройством. Затраты мощности дизеля на функционирование эжекционного устройства должны быть меньше, чем снижение ее от уменьшения плотности наддувочного воздуха при падении π к вследствие перераспределения энергии отработавших газов между турбиной и эжекционным устройством.

Однако нужно учитывать, что увеличение плотности посредством повышения π _к (через увеличение π _т) и/или увеличения Δ Т (через повышение u ) ведёт к увеличению π _п или то же самое к повышению р т , т. е. к уменьшению работы процесса расширения газов в цилиндре, а соответственно, к уменьшению мощности дизеля. Используемая расчетная модель не дает прямой связи между давлениями отработавших газов перед турбиной и в начале процесса выпуска, потому этот вопрос требует дальнейшей проработки.

Затраты мощности N в на циркуляцию охлаждающего воздуха через матрицу ОНВ по данным работ [19, 20]

N в = G^ ,                                                         (19)

Ров где Gов = u∙Gв – расход охлаждающего воздуха; Δр = р0 – рн – перепад давлений охлаждающего воздуха, создаваемый эжектором.

Разность значений ( Н э – N в / G в ) представляет собой потери энергии в эжекторе, обусловленные трением и диссипацией энергии при соударении смешивающихся потоков отработавших газов и охлаждающего воздуха.

Проведенное исследование свидетельствует, что:

• –    максимальное снижение температуры наддувочного воздуха можно обеспечить оптимальным распределением энергии отработавших газов между газовой турбиной и эжектором;

• –    максимальная плотность наддувочного воздуха может быть достигнута в том случае, если при одних и тех же затратах энергии на циркуляцию охлаждающего воздуха степень охлаждения НВ в случае применения эжекционного устройства будет больше, чем при применении, например, приводного вентилятора;

• –    возможность достижения максимальной мощности дизеля при использовании эжекционно-го устройства для циркуляции охлаждающего воздуха через ОНВ требует дополнительного рассмотрения.