Распределение микрочастиц диборида титана, введенных в алюминиевый слиток при помощи МГД-перемешивания кристаллизующегося расплава

Перспективным направлением в разработке новых конструкционных материалов является создание алюмокомпозитов [1–3]. Одним из путей их получения является введение армирующих микро- или наночастиц в жидкий алюминий и его последующая кристаллизация. Исследователями опробованы разные способы реализации этого процесса: инжектирование армирующих частиц в жидкий алюминий газовой или плазменной струей и механическое или МГД-перемешивание; введение частиц ультразвуковым воздействием на расплав; внедрение частиц в расплав на основе кавитации. Самым простым и дешевым, но, к сожалению, не самым эффективным способом внедрения частиц в жидкий алюминий служит их механическое замешивание при помощи механического импеллера или МГД-перемешивателя, создающего бесконтактное воздействие на металл электромагнитным полем [4–13].

Проблемой внедрения армирующих частиц в жидкий алюминий является его большое поверхностное натяжение и во многих случаях плохая смачиваемость частиц металлом. Для некоторых частиц из материалов (SiC, Al 2 O 3 , TiB 2 ) смачиваемость жидким алюминием может возрасти при повышении температуры расплава. Тем не менее, в большинстве случаев частицы, находящиеся на поверхности металла, не могут проникнуть в его объем даже при интенсивном перемешивании. Поэтому внедрение микрочастиц осуществляется либо приданием им большой скорости в плазменной струе, либо введением сразу внутрь объема посредством газового инжектирования или в составе брикетов (таблеток), состоящих из армирующих частиц, спрессованных в брикеты (таблетки) с алюминиевым порошком.

После добавления частиц для их равномерного распределения в объеме сплав интенсивно перемешивается, а затем кристаллизуется при непрекращающемся перемешивании. Следует отметить, что при введении частиц путем простого механического или МГД-перемешивания, часть их отторгается и выносится на поверхность. Вследствие этого эффективность процесса снижается.

Для получения алюмокомпозита важно равномерное распределение армирующих частиц в его объеме. С помощью бегущего и вращающегося магнитных полей можно создавать в объеме жидкого металла перемешивающие течения различной топологии и интенсивности [14–16]. Применяя МГД-перемешивание при создании алюмокомпозитов, можно также влиять на кристаллическую структуру получаемого слитка и дополнительно улучшать его свойства [11, 17, 18].

Как сказано ранее, из-за слабой смачиваемости некоторые частицы плохо внедряются в жидкий алюминий даже при интенсивном перемешивании, однако микрочастицы некоторых материалов, таких как TiB 2 , TiC, проникают в металл лучше [12].

Целью данной работы являлось исследование возможности введения в жидкий алюминий армирующих микрочастиц TiB 2 посредством МГД-перемешивания жидкого алюминия с его последующей кристаллизацией в условиях непрерывного МГД-перемешивания расплава, нахождение характеристик движения частиц и их распределения в объеме получаемого слитка.

• 2.    Численное моделирование

  • 2.1.    Постановка задачи

Теоретическая часть исследования заключалась в изучении движения как брикетов (таблеток), вводимых в объем алюминия в тигле, так и непосредственно самих армирующих частиц в процессе направленной кристаллизации алюминиевого слитка. Ввиду сложности задачи, включающей МГД-перемешивание, деформацию свободной поверхности, движение и растворение брикетов, образование и эволюцию континуума армирующих частиц, кристаллизацию металла и другое, одновременное моделирование всех процессов не рассматривалось. Численная модель создавалась разбиением основной (комплексной) задачи на нескольких более простых подзадач:

• –    подзадача A: расчет электромагнитного поля МГД-перемешивателя и лоренцевых сил, действующих на жидкий металл в тигле;

• –    подзадача B: определение формы свободной поверхности жидкого металла — воронки, формирующейся при его вращении;

• –    подзадача C: движение брикетов (таблеток) в перемешиваемом расплаве алюминия;

• –    подзадача D: эволюция континуума армирующих частиц и определение распределения частиц по объему жидкого металла в тигле.

Характерные времена длительности указанных процессов в тигле значительно меньше характерного времени движения фронта кристаллизации. Вследствие этого его продвижение не рассматривалось. Подзадача A решалась для полной области, включающей перемешиватель и тигель с кристаллизующимся металлом, решение подзадач B–D проводилось для части тигля, содержащей жидкий металл, нижняя твердая граница этой области (фронт кристаллизации) считалась неподвижной и плоской. Все вычисления выполнялись для моментов времени, в которые фронт кристаллизации находился на высоте 0, 0, 25 h , 0,5 h , 0, 75 h , где h — начальная высота недеформированной свободной поверхности металла в тигле.

Итак, рассмотрим особенности решения выделенных подзадач. Важным упрощающим математическую модель обстоятельством служит то, что скорости течения расплавленного металла в перемешивателе малы по сравнению со скоростями вращающегося и бегущего магнитных полей, а электропроводность расплава умеренная. Поэтому перенос магнитного поля посредством движущейся проводящей среды пренебрежимо мал. В связи с этим задачу нахождения электромагнитных сил (подзадача A) будем решать в низкочастотном приближении, без учета движения проводящей среды, и отдельно от задачи определения гидродинамических полей в перемешиваемом объеме (подзадачи B). В этом приближении из уравнений движения магнитной гидродинамики следует исключить описание токов смещения:

dD 6 t

= jjj << |j| =O|E + Ест | . (1)

Справедливы следующие оценки:

1 D ~ εε E ,      ~ ω ,

⁰ ∆ t

∆ D

∆ t

~ εε ₀ ω E .

Тогда для частоты и периода колебаний поля имеем:

σ ω <<    ,

εε0

T

εε

>>    0 ,

σ

где σ — электропроводность, εε₀ — диэлектрическая проницаемость.

В рамках указанных допущений запишем уравнения Максвелла:

∇×H=j, ∇×E=-∂B,   ∇⋅B=0, ∇⋅D=ρ,(4)

∂t которые дополним системой материальных уравнений:

D=εε0E,B= µµ0H, j=σE.(5)

На границе раздела сред поставим стандартные условия равенства нормальных компонент магнитной индукции и скачок тангенциальных компонент:

Bn1=Bn2,    1Bτ1= 1Bτ2.(6)

µ1µ2

Уравнения (4), (5) могут быть записаны в терминах векторного потенциала, который вводится соотношением B = ∇× A . При гармоническом законе изменения электрического тока в индукторах и при условиях однородности и отсутствия дисперсии среды электромагнитная задача существенно упрощается. Представляя зависимость магнитного поля и тока от времени в виде: A = A ₀ e^{i ω t} и j = j ₀ e^{i ω t} , сведем исходную задачу к стационарной задаче для комплексных амплитуд (полагая, что частоты бегущего и вращающегося поля одинаковы):

∇ ² A ₀ - i ωµµ ₀ σ A ₀ =-µµ ₀ j ₀.

Размеры расчетной области выберем из соображений, что на ее наружной границе Γ магнитное поле намного слабее, чем в зоне перемешивания жидкого металла. В этом случае для векторного потенциала используем граничные условия равенства нулю нормальной компоненты Γ :

A n I _Γ = 0 .                                                          (8)

В результате решения краевой задачи (7), (8) определим поле электромагнитных сил в жидком металле:

f em = Re j × B ^*.                                                (9)

Для вычисления поля электромагнитных сил (подзадача A) применялся пакет ANSYS MAXWELL 3D. Создавалась точная геометрическая модель МГД-перемешивателя и тигля, участвовавших в эксперименте (Рис. 1 a ). Расчётная область содержала МГД-перемешиватель ( 1 ), тигель с расплавленным металлом ( 2 ) и окружающую их дополнительную протяженную область, заполненную воздухом. Следует отметить, что в программном пакете предусмотрен автоматически выбор размера дополнительной области исходя из выполнения граничного условия (8). Все материалы, кроме стального сердечника, были неферромагнитные ( µ= 1 ), магнитная проницаемость сердечника считалась постоянной: µ = 2500 . К физическим параметрам, обусловливающим величину электромагнитного поля и не связанным с геометрией, относились токи в индукторах, частота тока, число витков в катушках. Их значения задавались близкими к значениям аналогичных величин, имевших место в эксперименте. В результате решения находилось поле лоренцевых сил в жидком металле, которое затем передавалось в программу решения гидродинамической задачи (подзадачи B). Решение подзадачи B давало измененную форму

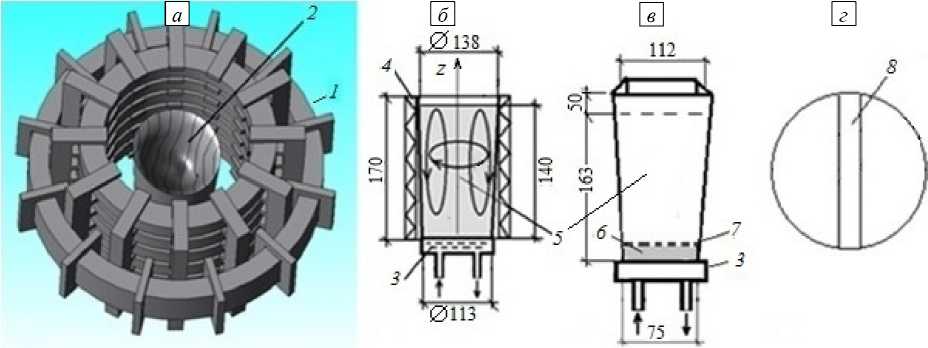
Рис. 1. Геометрия расчетной области в подзадаче A (размеры в мм) ( а ), конструкции тигеля круглого ( б ) и квадратного ( в ) сечения и схема продольной разрезки слитка ( г ); 1 – МГД-перемешиватель, 2 – тигель, 3 – водоохлаждаемое дно, 4 – кольцевой нагреватель (у тигеля квадратного сечения не показан), 5 – жидкий алюминий, 6 – слой микропорошка TiB 2 , 7 – алюминиевая пластина, 8 – пластина, вырезаемая из середины слитка

свободной поверхности жидкого металла, которая влияла на электромагнитное поле внутри расплава, поэтому снова решалась подзадача A. Таким образом, две подзадачи — A и B, рассматривались в цикле до установления электромагнитного поля и формы свободной поверхности, что обычно происходило за 3–4 итерации. На первой итерации в начальный момент времени жидкость в тигле считалась покоящейся, а свободная поверхность имела горизонтальную форму.

Трехмерная краевая задача течения жидкости (подзадача B) решалась в рамках двухфазной модели системы «расплав алюминия–воздух» со свободной границей посредством пакета ANSYS CFX. Уравнения переноса импульса в несжимаемой жидкости и учет турбулентности в рамках κ-ε модели имели вид:

∂v+(v∇)v=-1∇p+1∇⋅(νeff∇v)+fem ,     ∇⋅v=0.

Здесь ν _eff =ν+ν _T , где ν _T — турбулентная вязкость. Число Рейнольдса при скоростях 1 м/с составляет порядка 10⁵, что соответствует развитому режиму турбулентности. Стандартная κ-ε модель зарекомендовала себя как очень устойчивая, экономичная по отношению к вычислительным ресурсам и обладающая приемлемой точностью для широкого круга задач. За счет применения в ней пристеночных функций есть возможность использовать сеточные модели с невысоким разрешением вблизи стенок и получать при этом хорошие результаты. В методе пристеночных функций вязкий подслой и переходная область пограничного слоя не отыскиваются, а описываются полуэмпирическими формулами. Поэтому на данный момент эту модель можно рассматривать в качестве основной для решения большинства прикладных задач в области гидродинамики.

Геометрия расчетной области в подзадаче B представляла собой усеченный конус круглого сечения и воспроизводила форму и размеры тигля, используемого в экспериментах (Рис. 1 б ). Область была заполнена двухфазной системой «расплав алюминия–воздух». Граничные условия предполагали прилипание и непроницаемость жидкости на нижней и боковых твердых поверхностях тигля, на свободной границе использовалась модель поверхностного натяжения (Continuum Surface Force) из пакета ANSYS CFX, разработанной и изложенной в [19]. Сила поверхностного натяжения представляется в ней как объемная сила, сосредоточенная на границе раздела.

Рассмотрим границу раздела со свободной поверхностью. Определим первичную жидкость α (жидкую фазу) и вторичную жидкость β (обычно — это газовая фаза). Сила поверхностного натяжения, описываемая моделью поверхностной силы сплошной среды, равна:

F αβ = f αβ δ αβ ,                                                   (11)

где fαβ = -ζαβκαβnαβ +∇sζ,                                          (12)

при этом ζ — коэффициент поверхностного натяжения, n _αβ — вектор нормали к границе раздела, направленный от первичной жидкости к вторичной жидкости, ∇ _s — оператор градиента на границе раздела, δ_αβ — дельта-функция интерфейса, равная нулю вдали от границы раздела, κ — кривизна поверхности, вычисляемая по формуле:

καβ =∇⋅nαβ.

Слагаемые в правой части уравнения (12) отражают нормальную и тангенциальную составляющие силы поверхностного натяжения соответственно. Нормальная составляющая возникает вследствие кривизны поверхности раздела, а тангенциальная составляющая — из-за изменений коэффициента поверхностного натяжения (эффект Марангони).

Реализация модели поверхностного натяжения в уравнениях и граничных условиях производится в препроцессоре ANSYS CFX автоматически после того, как при описании задачи указывается, что в расчетном домене следует использовать модель двухфазной среды (Multiphase Flow), а на границе фаз модель поверхностного натяжения (Continuum Surface Force). При этом в программу вводится единственный количественный параметр — коэффициент поверхностного натяжения, который в обсуждаемой задаче имел значение ζ=0,072 Н/м.

В результате решения подзадачи B определялись структура и характеристики течения жидкого металла в тигле под действием электромагнитных сил (9). Топология течения зависит от интенсивности вращающегося и бегущего электромагнитных полей и для случая, рассматриваемого в настоящем исследовании, существенной компонентой движения жидкого металла в тигле является вращение с характерной скоростью 1 м/с. В таких условиях форма свободной поверхности меняется с плоской горизонтальной на криволинейную — воронкообразную. Поскольку изменения, происходящие в проводящей жидкости влияют на поле лоренцевых сил, производился перерасчет магнитной и гидродинамической задач; итерации продолжались до тех пор, пока свободная поверхность жидкого металла не принимала установившуюся форму. Расчетная сетка строилась с учетом того, что электромагнитные силы распределены по тиглю неравномерно вследствие скин-эффекта. Для жидкого алюминия при частоте 50 Гц поле проникает в металл на глубину 36 мм, и в этом скин-слое сосредоточены наибольшие градиенты электромагнитной силы и, соответственно, гидродинамических полей. Поэтому сетка сгущалась вблизи поверхности жидкого металла и содержала не менее 105 узлов.

Подзадачи C и D решались в рамках модели частиц в пакете ANSYS CFX (в подзадаче D использовалась модель дисперсных частиц). Одновременно с расчетом движения частиц производилось решение гидродинамической задачи определения параметров течения жидкого металла в поле электромагнитных сил. Гидродинамический расчет производился дважды. В связи с тем, что заложенную в ANSYS CFX модель частиц невозможно использовать для многофазных сред, пришлось разбить гидродинамическую задачу на подзадачи: B — определение формы свободной поверхности вращающейся жидкости в двухфазной системе «жидкий металл–воздух» и C, D — нахождение характеристик движения жидкого металла и содержащихся в нем частиц в однофазной системе с воронкообразной верхней границей, полученной в подзадаче B.

Движение частиц в физической и численной моделях пакета ANSYS CFX зависит от сил, действующих на исследуемую систему (см. [20]):

du

p mp dt =D +B +R +VM +P , где mp , up — масса и скорость частицы, FD — сила сопротивления, действующая на частицу, FB — Архимедова сила, FR — сила, связанная с вращением жидкости, FVM — сила виртуальной массы, заметная только для пузырьков, FD — сила градиента давлений. Для силы сопротивления использовалась модель из [21], удовлетворительно работающая для твердых частиц при числах Рейнольдса Re>1 . Помимо указанных сил, в данной задаче на частицу неявно влияла еще одна сила, обусловленная тем, что силы Лоренца действуют на жидкость, но не сказываются на частицах; эта сила создается электромагнитным полем, но опосредовано, через жидкость. Растворение брикетов с образованием армирующих микрочастиц в данных моделях не рассматривалось, то есть подзадачи C и D решались независимо друг от друга. Поскольку расчетное время для этих подзадач физически существенно меньше характерного времени кристаллизации, то предполагалось отсутствие массопереноса, связанного с захватом частиц твердой фазой.

При решении подзадачи C рассчитывалось движение 60 сферических частиц диаметрами 5–10 мм. Введение частиц (таблеток) производилось поочередно (1 таблетка в секунду) вблизи дна воронки на свободную поверхность расплава. В модели частиц из ANSYS CFX граничные условия учитывают взаимодействие частиц с твердыми стенками области, а также их столкновения частиц. В данной работе предполагалось, что таблетки упруго отражаются от стенок и друг от друга; трение отсутствует.

Начальные условия в подзадаче D предполагали концентрацию дисперсных микрочастиц в узком слое вблизи дна расчетной области.

• 2.2.    Результаты численного моделирования

Остановимся на результатах решения подзадач C и D. Все результаты получены для полей B _RMF = 8,08 мТ, B _TMF = 12, 96 мТ (поле бежит вниз), создаваемых трехфазными токами с частотой 50 Гц I _RMF = 8 A, I _TMF = 12 A. Здесь и далее нижними индексами RMF и TMF обозначаются, соответственно, величины вращающегося и бегущего магнитных полей.

На рисунке 2 приводятся траектории одного из брикетов (таблеток) для разных положений фронта кристаллизации. Начальное положение таблетки выбрано возле дна воронки свободной поверхности, хотя следует отметить, что таблетки достаточно быстро — за несколько секунд — поднимаются к свободной поверхности вблизи края воронки, и через несколько секунд движения их траектории практически не зависят от начального положения. Таким образом, таблетки, содержащие армирующие микрочастицы, при МГД-перемешивании движутся в объеме жидкого алюминия около его поверхности, растворяются и отдают микрочастицы в этой области жидкому металлу. Нерастворившиеся части таблеток при кристаллизации алюминия в условиях МГД-перемешивания «вмораживаются» в слиток у его поверхности.

При решении подзадачи D о поведении при МГД-перемешивании армирующих микрочастиц выяснилось, что частицы довольно быстро, за несколько секунд, равномерно распределяются по всему объему жидкого металла. Поэтому точка ввода частиц как-будто не должна играть большой роли. Полагалось, что частицы в начале процесса образуют слой на дне тигля.

Рисунок 3 содержит распределения микрочастиц для разных положений фронта кристаллизации. Физическое время счета 120 с. Рисунок свидетельствует, что дисперсная фаза хорошо перемешана и близка к равномерному распределению. Наблюдается лишь небольшое увеличение концентрации частиц в центре верхней части слитка на конечной стадии его кристаллизации (Рис. 3 в ).

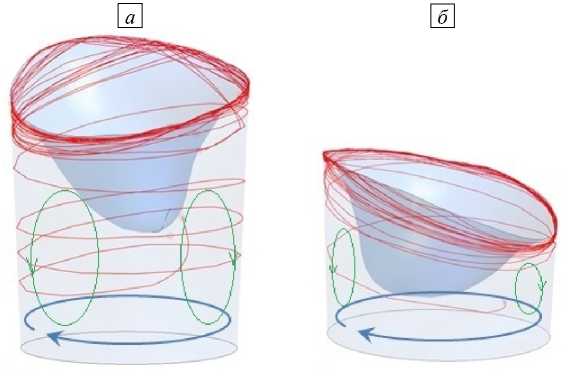
Рис. 2. Траектории частиц диаметрами, [мм]: 10 ( а ), 7.5 ( б ), 5 ( в ) через 20 с после начала движения; жидкий металл занимает, соответственно, 100, 50, 25% от первоначального объема; линиями со стрелками показано направление движения расплава, тонкая линия – траектория частицы в расплаве

в

б

в

Рис. 3. Плотность распределения дисперсной фазы (частиц диаметром 3 мкм); жидкий металл занимает от первоначального объема, [%]: 100 ( а ), 50 ( б ), 25 ( в )

3.    Эксперимент

Экспериментальная установка подобна описанной в [13] и показана на рисунке 1 a – в . Тигель — ее главная часть, изготовлен из листа нержавеющей стали и снабжен водоохлаждаемым дном. Боковые стенки тигля обогреваются кольцевым нагревателем мощностью 1200–1250 Вт, а внутренняя поверхность защищена специальной обмазкой от воздействия жидкого алюминия. Тигель устанавливается в рабочем объеме (высота 300 мм, диаметр 200 мм) МГД-перемешивателя, который создает бегущее (волновое число 20,9 м^–1) и вращающееся (с частотой 50 Гц) магнитные поля (Рис. 1 a ). Источник трехфазного (50 Гц) тока для питания индукторов поддерживает регулируемый непрерывный режим их работы.

Рис. 4. Порошок TiB 2 (1–5 мкм) ( а ) и порошок Al (100–150 мкм) ( б ); снимки сделаны на растровом электронном микроскопе FEI Quanta 650FEG

В ходе эксперимента в печи сопротивления в графитовом тигле расплавлялся алюминий, температура которого доводилась до 807–900 С°. Затем сплав заливался в тигель (Рис. 1 б , в ), установленный в МГД-перемешивателе, индукторы которого (бегущее и вращающееся поля) уже были включены и создавали заданный режим перемешивания. Кольцевой нагреватель, окружающий боковые стенки тигля, тоже был включен. В экспериментах опробовано два варианта введения микрочастиц в жидкий алюминий. В первом из них армирующие микрочастицы TiB 2 (1–5 мкм, Рис. 4 а ) в составе таблеток, спрессованных с порошком алюминия (100–150 мкм, Рис. 4 б ) вбрасывались в жидкий алюминий; тигель имел круглое сечение (Рис. 1 б ). Во втором варианте микрочастицы TiB 2 изначально располагались на дне тигля квадратного сечения (Рис. 1 в ), прикрывались алюминиевой пластиной, и после этого в тигель заливался алюминий.

По истечении 20–30 мин МГД-перемешивания включалось водяное охлаждение дна тигля и при непрекращающемся перемешивании осуществлялась направленная кристаллизация алюминия. Закристаллизовавшийся слиток вынимался и разрезался вдоль, согласно схеме (см. Рис. 1 г ). Структура поверхности части слитка, изъятой из его середины, исследовалась на цифровом оптическом микроскопе Hirox KH-7700, а также на растровом электронном микроскопе FEI Quanta 650FEG. Сделанные снимки позволяют судить о структуре полученного материала, а также о характере распределения вносимых в объем металла микрочастиц.

В экспериментах, как уже упоминалось, применялись два варианта введения микрочастиц в жидкий алюминий при его МГД-перемешивании. В первом варианте использовался тигель круглого сечения (Рис. 1 б ). В жидкий алюминий, разогретый до 820°С и перемешиваемый бегущим вниз ( B _TMF = 12, 96 мТ) и вращающимся ( B _RMF = 8,08 мТ) магнитными полями, вбрасывались таблетки состоящие из спрессованных с алюминиевым порошком (150–200 мкм) микрочастиц TiB 2 . При этом таблетки, попавшие во вращающийся жидкий металл, увлекались им и хорошо затягивались в его объем. Однако даже после 20–30 мин перемешивания таблетки «растворялись» не полностью, часть их выносилась к поверхности, где они «вмораживались» при кристаллизации слитка (Рис. 5). Такое поведение крупных частиц при МГД-перемешивании согласуется с результатами расчетов авторов, приведенных на рисунке 2. Как показал эксперимент, наилучшим образом в жидком алюминии растворяются таблетки, содержащие только 10–15% микрочастиц TiB 2 .

Во втором варианте микрочастицы TiB 2 укладывались слоем на дне пустого тигля, прикрывались алюминиевой пластиной, имеющей толщину 1 мм (Рис. 1 в ). Затем жидкий алюминий при температуре 900°С заливался в тигель, и подвергался МГД-перемешиванию с последующей направленной кристаллизацией. При таком варианте на начальном этапе в придонной части тигля возникала большая концентрация частиц. Для усиления переноса частиц в некоторых экспериментах использовался тигель квадратного поперечного сечения. Такая конфигурация тигля хотя несколько и снижала скорость потока при перемешивании металла, но вызывала дополнительную турбулизацию его течения, что приводило к интенсификации переноса, по сравнению с тиглем круглого сечения [22, 23]. Как показали эксперименты, квадратная форма сечения тигля слабо влияет на зависимость твердости композита от концентрации в слитке армирующих частиц (Рис. 6), а также на зависимость его локальной твердости от высоты (Рис. 7).

б

Рис. 5. Левая половина продольного сечения алюминие слитков с введенными микрочастицами TiB2; результирующая концентрация микрочастиц оценивается, [%]: 3,1 (а), 2,5 (б); в верхних частях слитков видны части нерастворившихся таблеток; наблюдается уменьшение размеров зерна в структуре слитка круглого сечения при увеличении расстояния от дна до поверхности

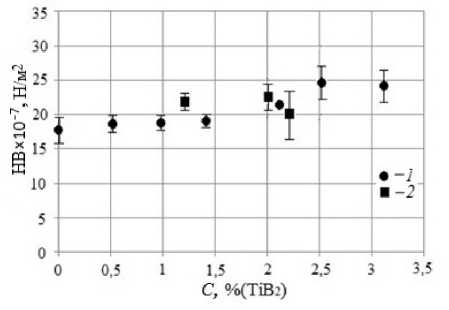
Рис. 6. Зависимость средней по продольному сечению слитка твердости (по Бринеллю), установленной стандартным способом, от концентрации введенных в слиток МГД-перемешиванием микрочастиц TiB 2 (1–5 мкм); слиток с круглым (символы 1 ) и квадратным ( 2 ) сечением

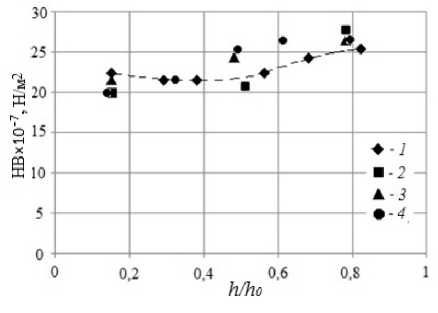
Рис. 7. Зависимость от безразмерной высоты твердости (по Бринеллю) алюминия А0 с концентрацией микрочастиц TiB 2 : 0% (символы 1 , соединенные штриховой линией), то есть без введения микрочастиц; 2% ( 2 ); 2,5% ( 3 ); 3,1% ( 4 ); данные 1 , 3 и 4 для слитков с круглым сечением (частицы введены в состав в виде таблеток), данные 2 для слитка с квадратным сечением (частицы введены из придонного слоя порошка)

4.    Результаты экспериментов

Электромагнитное перемешивание алюминия при его кристаллизации приводит к уменьшению размеров зерна в структуре слитка и как следствие увеличение твердости металла [18]. Как показал наш эксперимент, увеличение концентрации введенных в алюминий микрочастиц TiB 2 так же приводит к небольшому увеличению его твердости (Рис. 6). Предполагаемая концентрация микрочастиц в слитке рассчитывалась путем учета чистого веса вводимых в алюминий микрочастиц и учета не растворившихся частей таблеток с микрочастицами или отторгнутого порошка микрочастиц после кристаллизации слитка.

Эксперимент показал, что в центральной части слитка наблюдается повышение твердости металла по мере удаления от его донной части. На рисунке 7 представлена зависимость твердости алюминия по Бриннелю от безразмерной высоты, где h 0 = 110 мм — размер интервала (отсчет от дна слитка), на котором измерялись значения твердости металла. Из рисунка видно, что в слитке, не содержащем микрочастицы, твердость увеличивается с высотой. Это можно объяснить тем, что с высотой в структуре слитка уменьшается размер зерна (Рис. 5), что и приводит к росту твердости. Однако в слитках, содержащих микрочастицы TiB 2 , твердость с приближением к поверхности слитка растет несколько быстрее. Этот факт, с учетом результатов эксперимента на рисунке 6, можно объяснить небольшим ростом с высотой локальной концентрации микрочастиц. На рисунке 8 приведены полученные на электронном микроскопе картограммы участков размерами 300 x 300 мкм в продольных сечениях слитка в разных по высоте точках с концентрацией частиц TiB 2 2 и 2,5%. Светлыми точками на картограммах обозначен титан, присутствующий в микрочастицах.

По фотографиям, сделанным на разной высоте продольного сечения слитков, производился подсчет частиц на участках размером 300 x 300 мкм. В результате можно видеть (Рис. 9), что количество частиц на исследуемых площадках наблюдения увеличивается в верхней части слитка.

Рис. 8. Картограмма области (300 x 300 мкм) в нижней точке среднего сечения слитков ( а , в ) и в верхней точке среднего сечения ( б , г ) слитка алюминия А0 с введенным микропорошком TiB 2 (1–5 мкм); концентрация микропорошков в слитках: ( a , б ) – 2% (слиток квадратного сечения, введение частиц из придонного слоя); ( в , г ) – 2,5% (слиток круглого сечения, введение частиц в составе таблеток)

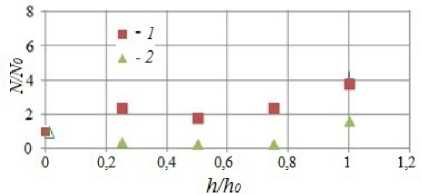
Рис. 9. Зависимость безразмерного числа микрочастиц N/N о на площадке наблюдения (300 x 300 мкм) от безразмерной высоты hh ₀ ; N – число частиц на площадке, находящейся на высоте h , N ₀ – число частиц на площадке на нулевой высоте; h – расстояние от первой точки у дна слитка до точки наблюдения; h ₀ – длина интервала, на котором производилось наблюдение. 1 – слиток круглого сечения с концентрацией микрочастиц (TiB 2 ) 2,5%, введенных в состав таблеток; 2 – слиток квадратного сечения с концентрацией микрочастиц (TiB₂) 2%, введенных из слоя микрочастиц на дне тигля

Введение микрочастиц в эксперименте, которому соответствует кривая 1 на рисунке 9, производилось путем вбрасывания на поверхность расплава алюминия таблеток, содержащих микрочастицы. Можно видеть, что наименьшее содержание частиц приходится на придонную область, где скорость движения жидкости минимальна. На небольшой высоте от дна число частиц возрастает и далее практически не меняется и только у поверхности их снова становится больше. В эксперименте, в котором микрочастицы вводились из слоя порошка со дна тигля (Рис. 9, кривая 2 ), концентрация частиц с высотой слитка меняется по-другому: концентрация микрочастиц у дна тигля, где располагается слой порошка, высокая; затем, на небольшой высоте над дном, она падает; далее концентрация не меняется; а у поверхности слитка она опять возрастает. Такая, слабо меняющаяся, концентрация в ядре слитка и ее увеличение вблизи поверхности качественно согласуется с результатами численного моделирования, приведенных в разделе 2 статьи.

5.    Заключение

В результате проведенных экспериментов выяснилось, что возможны два простейших варианта введения армирующих микрочастиц TiB 2 (1–5 мкм) в алюминиевую матрицу при непрерывном МГД-перемешивании жидкого алюминия с его последующей направленной кристаллизацией.

В первом варианте микрочастицы TiB 2 вбрасываются в жидкий металл в составе таблеток, спрессованных вместе с алюминиевым порошком (100–150 мкм), причем содержание микрочастиц TiB 2 , для лучшего растворения таблеток, не должно превышать 15%. В этом варианте по окончанию МГД-перемешивания и направленной кристаллизации часть таблеток растворяются не полностью. Во втором варианте микрочастицы изначально располагаются слоем на дне тигля и прикрываются тонкой алюминиевой пластиной, после этого в тигель вливается жидкий алюминий и производится МГД-перемешивание с последующей направленной кристаллизацией расплава. Надо отметить, что в обоих вариантах концентрация армирующих частиц в затвердевших слитках не превышала 4% от их массы.

Эксперименты по введению большего количества микрочастиц в слиток приводили к увеличению объема нерастворившихся таблеток или отторгнутого порошка микрочастиц.

Как показал физический эксперимент, крупные частицы (таблетки и недорастворившиеся их части) собираются в верхней части жидкого металла, вблизи свободной поверхности. Численный эксперимент позволил установить, что микрочастицы практически равномерно распределяются по объему жидкого металла, с небольшим увеличением концентрации частиц вверху в центральной части закристаллизовавшегося слитка. Физический эксперимент выявил (Рис. 9, кривая 1 ) относительно равномерное распределение концентрации микрочастиц с небольшим увеличением концентрации по высоте в ядре слитка. Последнее, вероятно, объясняется скоплением таблеток, которые являются источниками микрочастиц в приповерхностном слое.

При втором варианте ввода микрочастиц наблюдается (Рис. 9, кривая 2 ) большая, чем в ядре, концентрация в придонной части слитка, что, по-видимому, обусловлено влиянием начальных условий, при которых слой микрочастиц располагается на дне тигля.

Работа выполнена в соответствии с госбюджетным планом AAAA-A19-119012290101-5 ИМСС УрО РАН (разделы 1, 2), а также при поддержке РФФИ и Пермского края (проект № 19-48-590001 р_а (разделы 3, 4).