Распределение температуры в трехслойной полупроводниковой структуре при воздействии на нее локально распределенной поверхностной тепловой нагрузки

Ульяновское отделение Института радиотехники и электроники РАН

Приведена математическая модель температурных полей, образующихся в трехслойных полупроводниковых структурах прямоугольной формы, при воздействии на внешний слой кристалла локально распределенной поверхностной тепловой нагрузки, которая возникает в результате неустойчивости однородного распределения тока и приводит к пробою полупроводниковой структуры. Проведена оценка возможностей аналитического решения поставленной задачи. Найден алгоритм численного решения и представлены результаты расчетов и их сравнение с результатами эксперимента.

Определение теплофизических характеристик полупроводниковых элементов радиоэлектронной техники связано с проведением теоретических исследований температурных и термодеформационных полей, возникающих при нагреве слоистых полупроводниковых структур с локально распределенными поверхностными источниками тепла. Такое исследование становится важным при определении предельных возможностей устройств микроэлектроники, использующих эти структуры в качестве активных элементов, которые могут работать как в импульсном, так и непрерывном режимах. Известно [1], что при работе мощных транзисторов в импульсных режимах, тепло в коллекторном переходе выделяется в основном на фронтах импульса. Максимальная температура, которая при этом достигается, может значительно превосходить среднюю температуру. При запирании транзистора в некоторых режимах может произойти застревание на фронте в определенных равновесных точках. При этом возникает условие неустойчивости тока по сечению эмиттера. Весь ток стягивается в узкий шнур, что приводит к возрастанию выделяемой в единице объема мощности, плавлению активной области кристалла и выходу из строя элемента. При интенсивных нагревах тела за короткий промежуток времени, практически всегда существует зависимость теплофизических характеристик материалов от температуры, при этом необходи мо решать нестационарную нелинейную задачу теплопроводности, с локально распределенными поверхностными источниками тепла, математически представленными в виде обобщенной функции. Решение такой задачи, даже для одномерного случая, представляет определенные трудности [2]. Однако для проведения структурно-системного анализа и возможности решения обратных задач требуется найти более точное описание температурных полей, возникающих в многослойных средах, а также их изображений, полученных в результате интегральных преобразований.

Рассмотрим модель трехслойной полупроводниковой структуры, в качестве слоев которой можно выбрать: полупроводниковый кристалл, припой и кристаллодержатель.

Геометрические размеры слоев изменяются в следующих пределах:

(0 < x < 1 1 ), (0 < y < l ₂ ) ,

(l3(i-1) < z < l3i), где i = 1,2,3 - номер слоя.

Считаем, что тепло передается посредством теплопроводности, то есть температуры перегрева являются относительно низкими. Температурное поле определяем без учета деформации слоев, полупроводниковая структура ведет себя как упругая. В этом случае в уравнениях теплопроводности отсутствуют члены, учитывающие взаимосвязь между тепловой и механической энергиями.

Нестационарные уравнения теплопроводности для такой многослойной среды будут

Pi(Ti)Oi(Ti)-i^ = V(Xi(Ti)VTi), (1) dt где Ti = Tci - T0 - избыточная температура; Tci, To - температуры i-го слоя и окружающей среды соответственно; Xi,ci,pi - коэффициенты теплопроводности, удельной теплоемкости, плотности i-го слоя; r = r(x,y,z) - радиус-вектор рассматриваемой точки.

Примем, что зависимость теплофизических характеристик слоев от температуры слабая [3], тогда (1) можно записать как dTL = aj AT dt        i i’

где а_i = X i / c i P i - коэффициент температуропроводности.

Начальное условие

T i (x, y, z, 0) = 0. Граничные условия

X^

¹ dz

-q^xt),

z = 0

q ( x , y , t ) = ^ дД x , y ) U j ( t ).     ⁽⁵⁾

j = 1

Опуская индекс j, пространственную и временную части этой функции запишем как q ( x У ) = JJ q o ⁽x , h ^{) d ( x -} x ^{) d (} У ^- hM dh ,^) ( s ® 0)

U = jr [ u ( t - nt - t o ) - u ( t - t „ - nt - t o )], ⁽⁷⁾ n = 0

где

4 0 (5, n) = P⁰^          (8);

^{n r} 0

P₀ - тепловая мощность j-го источника; r₀ -радиус теплового пятна, получающегося от действия j-го источника; о- площадь теплового пятна; u(t) - единичная функция Хевисайда; т - период последовательности импульсов; T u - длительность импульса; t₀ - время начала действия j - го источника; n - число импульсов. Применение к функциям T(x, y, z, t) и q(x, y, t) в задаче (2)-(4) интегрального косинус преобразования Фурье по координатам x, y и преобразования Лапласа по времени, приводит к следующим выражениям для изображений температур

T i2 (k,m,z,p), ^есёи I 33 ^^ ^:

dT i dx

= dT i x = 0,1 1     ^d y

= 0, y = ^0,l2

T ,2 = [ s .chfc. - z )УХ) + k i2 S 2shfo. - z ) Ж j T        [ s , sh^ _3] Ж ) + k , ₂ S ₂ ch ( l ₃₁ Ж j

T i (x,y,l 33 ,t) = 0

и условия сопряжения

T 22 = ^(fa ^- z X/pT )+ г-Лк - z X/pT ) I ^T         h. sh ( I 31 VP ? ) + k 12 S 2 =h ( 1 31 VS T ) ]

1    dT i - 1

^X i-1^— dz

, 3Ti =X z-1          dz z=l3(i-1)

, z=l3(i-1)

^T 32 =                                     (9)

^T     S 1 Sh ( 1 ,1 VT) + k 12 S 2 ch ( 1 31 vr)] ’

Ti-1 (x, y, l3(i-i) , t) = Ti (x, y, l3(i-i) , t) , где

(i = 2,3) ,                (4)

где q(x, y, t) - плотность теплового потока; A - оператор Лапласа в декартовой системе координат.

Если на поверхности (XY) действуют J источников тепла, то плотность потока тепловой энергии можно представить следующим образом:

S 1 = ch ( ( I 32 -

e i =

^{p + a} ikm

^

;

/

V ai a ikm

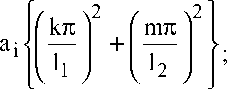
l 31 X/P T ^{)+ k} 23 ^{sh (} ( l 32

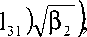
S 2 = Sh ( ( 1 32 —

l 31 Х/Р Г ^{)+ k} 23 c ^{h (( 1} 32

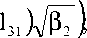
_k . । i ПС T _ q 2 ⁽ k.m) ^(И) ' I - V ₽ i - i ^;        I Тр

а изображения выражений (6) и (7) будут

q₂       к л х_о    m л у₀ . k ^ ²r

— _ cos---⁰cos---⁰ Sin--- ⁰

q 0           l 1          l 2          2l 1

sin

m n ²r

2l 2

4P 0 l 1 l 2

q0 = _31 _   2 , n kmr0

e ^{- t0} p ( 1 - e ^-T u p )

^{U (p) _} p ( i - e - t p ) , ^k,m = 1,2,_, to

Если к исходной задаче применить интегральные косинус преобразования Фурье по всем трем пространственным координатам, то после преобразования по коорди

Функции ф1(t) определяются следующим образом ф1(t) _^ [q2(k,m,t) + (- 1)n ■ Ф1(1)],

^Ф 2 ^(t) = I²" ^{[(- 1 ) n} ■ Ф 2 ^{(t) -} Ф 1 ^{(t) ]} ,

Ф 3 t) = a ³ Ф 2 t)

^ 3

А функции Ф('-1) (t) находятся из системы интегральных уравнений tt

J K (t,^) ■ Ф 2 (^)d^ - J K 1 (t, ^) ■ Ф 1 (^)d^ =Q(t),

t t

J K 4 (t, ^ ) ■ Ф 2 ( ^ )d ^ + J K 3 (t, ^) ■ Ф 1 (^)d^ = 0, (11)

нате z равному

⁽¹3i ^- l 3(i - 1) )

T i3 _ J     T i2

cos

V

nnz

⁽¹ 3i ^- l 3(i - 1) )

A _ dz ,

(l33

(i * 3),

где ядра интегральных преобразований и функция Q(t) будут

K 1 ^(t, ^ )= I J-„k I l. ^ )+ ^E 2kmo ^(t, ^ ^{) +}

+2 УК ■ E 1kmn t,^)+ E 2kmn t,^ )}, n=1

T33 _

- 1₃₂)

J

, (

T 32 ■ cos ^V

(2n - 1 )nz

²⁽¹ 33 ^- l 32 )

A -dz

TO

K(t, ^) = E,k 0(t, ^) + 2 У H)n E,k (t, ^), 2\           2km0v ’                        2kmnv ’ n=1

где

Ti2=Ti2(k,m, z, t), Ti3=Ti3(k,m,n,t),

K , (t, ^ ) = F 3 . K 2 (t, ^ ),  K , (t, ^ ) = 2

£{ E 3k.n t, 5 ) - F 3 ' E 2kmn t, 5 ) } - n = 1

^{z _ z -} l 3(i - 1) , ⁿ = ^1,2,^^, ^ , получим уравнение для нахождения изображения T,:

i3

dT dt + а ikmnTi3 _ф i(t) ,     (10)

с начальным условием T ,3 1₁_ о = 0 , где

^{- F} 3 ^ ^E 2km0 ^(t, ^ )’

J

Q(t) = F 2 У ^q2 j (k, m){W(t, 0) +

² j = 1

^a ikmn _

Г ^{к л} А ² Г — +

ai

V l i 7

V

mn l2

A ² Г +

nn

_A ²

+2 У ( ^- 1) n W(t, n)}.

n = 1

В этих формулах:

^E ikmn ^(t, ^ ) = ^exP^{{- a} ikmn ^(t- ^ ^)},

_V ⁽¹ 3i ^- l 3(i - 1) ) 7

F i =

ay -O ¹ i ⁽¹ 3i

-

l 3(i - 1) )

(i * 3),

a i ¹ (i - 1) ⁽¹ 3(i - 1)

-

l 3(i - 2) ) ’

a.

a3kmn a3

² k n

^V l ^{1 7}

Г +

V

m n l2

A ²

■Г -^ n 7 ²

e “ 1kmn ^T j ^{+ T} 0j )

-

V 2 1 33

-

l₃₂ ) 7

.

W(t, П) = П    ^“1kmn T j a1kmn e

e ^a 1kmn ^{(t T} oj

-

1) e ^ 1kmn ^T uj

-

) )

1) ^{- 1} .

На основании проведенных выше ана-

литических исследований нестационарной задачи телопроводности распространения тепла в трехслойной среде видно, что решение будет являться сложной функцией, не совсем пригодной для последующего качественного анализа. Было проведено численное решение задачи. При составлении конечно-разностных уравнений, из-за трехмерности задачи по пространственным координатам, предпочтение отдавалось явной схеме [4].

В конечных разностях рассматриваемая задача будет выглядеть следующим образом.

Если обозначить через U s, j,m,k значение функции T(x, y, z, t) в узлах сетки, где i, j, m -индексы узлов по координатам x,y,z соответственно, k - временной индекс, а s=1,2,3 -номер слоя, причем i=0,1,...,(I+1); j= 0, 1, ..., (J+1); m=0,...,(M_s+1); k=0,1,...,r, (12)

h2

to- —; tos

2l s

Начальное условие

h s ²

2l

.

^U i,j,m,0 =⁰ (m=^1,2,^^,M s ⁺¹),

^U i,j,0,0 ^— "^- q i.j.o .              (14)

Граничные условия

^U . = ' k ^U I+1,j,m,k = j ;

^U i,1,m,k = ^U : ^U .  . = J

U1 • n . - U1 • . , + — q; ;v;

i,j,0,k i,j,i,k X i ^4i,j,k

ijM +i,k

Условия сопряжения

U® . - U ^{s - i}     ;

i,j,0,k      i,j,Ms,k

- 0.

(s=2,3),

т _ l 1 . т _ l 2 . M — ⁽^^3s   '^3(s I) ) .

a I - ; J - 7^; M s =           ;

h h            h _s

т r=Г

Us • 1 г - Us - м v + i.jAk      i,j,M s - i ,k

где h - шаг по координатам x и y, h s - шаги по координате z, l - шаг по рассматриваемому промежутку времени т, то уравнение (2) будет (индекс s опускаем)

U i _J ,m,k ₊ 1 =^K 1 CU i-1 _J ,m,k ⁺U i ₊ 1 _J ,m,k ^{+ U} . ^+U i,j+1,m,k )⁺

^ ^Г m . 'U ... ^'^ U ..^^

Коэффициенты формулы (13) равны

K -          as tos

• ^{1     ( toto} s ^{+ 2} a s ^to s ⁺ a s Ю) ’

as to k2 ------------s;

^{( toto} s ^{+ 2} a s ^to s ⁺ a s ^{to )}

K _- (toto s - 2a s to s - a s to) _;

• ^{3     ( toto} s + ^2a s ^to s ⁺ a s ^to) ’

. ^Xs-i^hs /т Ts-i

⁺ Xh , ^(Ui,j,M s - i +i,k s s -i             ^s

Us-i      )

Ui,j,M s - i ,k⁾

Расчет проводился для трехслойной среды: 1) кристалл - Si; 2) припой - (Pb+Sn); 3) кристаллодержатель - Cu. Теплофизические свойства слоев приводятся в таблице.

Геометрические размеры в плоскости (XY) были равны l1=l2=6T0-3 м, число точек I=J=Ms=5. При этом для лучшей аппроксимации в условиях сопряжения (16) между слоями были взяты дополнительно еще две точки. Шаг по времени выбирался из критерия устойчивости алгоритма l < min'

h ² h 2      1

2a_s^2h 2 +h ² )

Таблица.

	l , (Bt/m - K)	c, (Дж/кг - К)	r,3 (êã/ì3)	òîëùèíà, (ì)
êðèñòàëë – Si	100	790	2,3 - 10 3	0,45 - 10-3
ïðèïîé – (Pb + Sn)	50	150	8,5 - i03	0,05 - 10-3
êðèñòàëëîäåðæàòåëü - Cu	400	400	8,9 - 103	1,5 - 10-3

а)

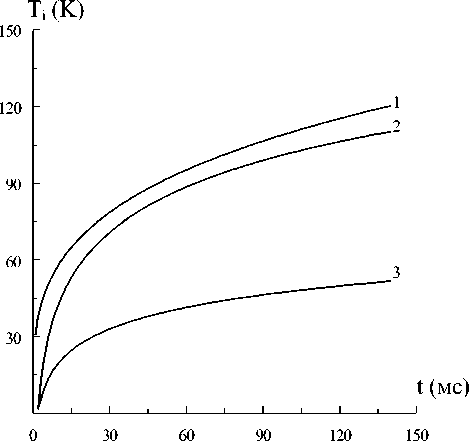
Рис. 2. Зависимость температуры слоев от времени: 1 -z=0мм, 2 - 0,475, 3 - 1,25

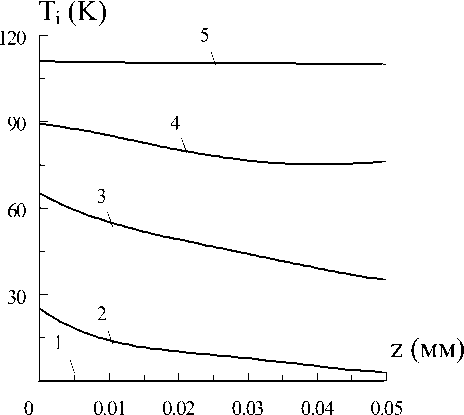
б)

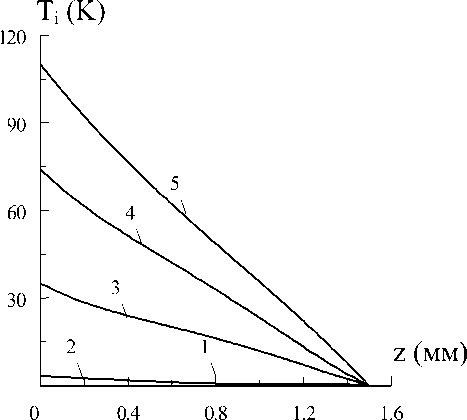
в)

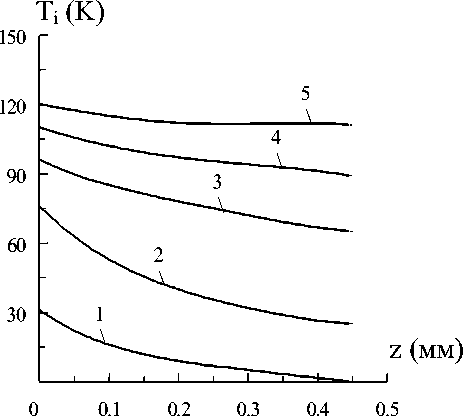
Рис. 1. Распределение температуры по слоям: а) - 1 слой, б) - 2, в) - 3; 1 - t=1мс, 2 -20, 3 -50, 4 - 90, 5 - 140

На рис.1 представлены распределения температур по толщине слоев для различных моментов времени.

Тепловая мощность источника составляла Р=50 Вт, расположение источника в центре поверхности внешнего слоя (i = 2, j = 2), начальная температура Т0=293К.

Зависимости температур слоев от времени показаны на рис.2. Кривая 1 построена для внешней поверхности первого слоя, а 2 и 3 для средних сечений второго и третьего слоев. Расположение и мощность источника те же, что и на рис.1.

Из последнего графика видно, что при заданной мощности температура полупроводникового кристалла достигает предельно допустимой за время порядка 140мс, что хорошо согласуется с экспериментальными данными T = 400K [5].