Распределение жевательной нагрузки по зубному ряду при центральной окклюзии

Любое жевательное движение заканчивается окклюзией. При окклюзии возникают силы контактного взаимодействия зубов верхней и нижней челюстей. Наибольших значений жевательная нагрузка достигает при центральной окклюзии. При расчете на прочность зубных протезов, а также зубных коронок после терапевтического лечения важно знать, как распределяется жевательная нагрузка по зубному ряду. Информация о распределении нагрузки по зубному ряду при центральной окклюзии позволяет также оценить роль каждой пары антагонистов в акте жевания, что является основой статического метода оценки жевательной эффективности зубочелюстной системы по Н.И. Агапову [1].

В данной статье рассматривается аналитический способ решения задачи о распределении жевательной нагрузки по зубному ряду. Этот способ основывается на следующих предположениях:

• -    височно-нижнечелюстной сустав рассматривается как цилиндрический шарнир;

• -    периодонт рассматривается как тонкий упругий изотропный винклеровский слой, а зубы и альвеолярные лунки как абсолютно твердые тела;

• -    поверхности контакта всех зубов находятся в одной окклюзионной плоскости, а силы контактного взаимодействия пар антагонистов перпендикулярны этой плоскости;

Фатеева Наталия Александровна, магистр биомеханики, кафедра теоретической механики, Пермь

• -    корни всех зубов имеют форму кругового конуса с радиусом основания r и высотой конуса h , ось которого перпендикулярна окклюзионной плоскости.

В работе приведен пример расчета с помощью полученных формул распределения нагрузки по зубному ряду на основе имеющихся в литературе данных по геометрии зубочелюстной системы и упругим свойствам периодонта, а также данных собственных измерений.

Аналитическое решение задачи

Как отмечено выше, периодонт рассматривается как тонкий упругий изотропный винклеровский слой, лежащий между двумя абсолютно твердыми телами. В соответствии с гипотезой Винклера связь между давлением p , действующим на упругий слой, и его прогибом w (рис. 1) имеет вид

p = kw.

Найдем величину коэффициента упругого основания k , исходя из выдвинутых выше предположений.

В соответствии с моделью Винклера отличной от нуля является только одна компонента тензора напряжений σz , о z = - p, и одна компонента тензора деформаций εz , которую, учитывая, что толщина слоя δ достаточно мала, можно найти по формуле

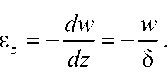
dw w

--=-- dz δ

Записывая закон Гука для изотропной среды с использованием постоянных Ляме λ и µ:

о z = (Х+2ц)8 z , получаем

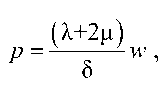
δ

δ

Рис. 1. Действие распределенной нагрузки p на упругий слой

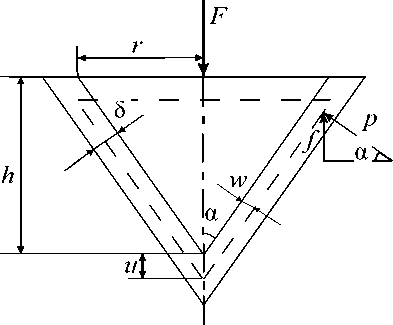
Рис. 2. Перемещение корня зуба в периодонте под действием жевательной нагрузки

откуда следует выражение для коэффициента упругого основания p =

( Н2ц )

w, δ откуда следует выражение для коэффициента упругого основания k (л-2и) =   E (1-v)

δ     (1+ν)(1–2ν)δ , где E – модуль Юнга, а ν – коэффициент Пуассона.

Полученная формула позволяет найти коэффициент жесткости периодонта корня зуба C в зависимости

F = Cu ,

связывающей силу F , действующую на зуб, и перемещение u этого зуба (рис. 2).

Действительно, нормальная к поверхности корня зуба составляющая перемещения определяется выражением w = u sin a .

Она порождает со стороны периодонта упругую реакцию p , величина которой определяется формулой (1). Осевая составляющая этой реакции может быть найдена по формуле f = p sin a.

Поскольку реакция периодонта распределена равномерно по поверхности корня зуба, интегральная величина этой реакции, равная по модулю силе F , действующей на зуб, может быть найдена по формуле

F = f • nr ².

В результате получаем

22    ^r

F = nr ku sin a = nk—;---utt, r2 + h2

откуда имеем выражение для коэффициента жесткости периодонта корня зуба

C = n k ^-y .                          (4)

r ² + h ²

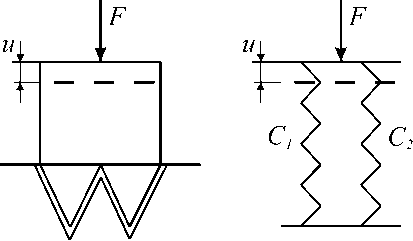
Рис. 3. Определение жесткости периодонта для многокорневого зуба

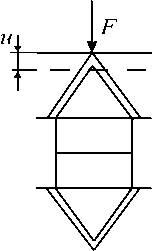
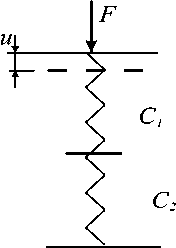
Рис. 4. Определение жесткости периодонта для пары антагонистов

Учитывая, что многокорневой зуб можно воспринимать как параллельное соединение пружин (рис. 3), приходим к выводу, что для многокорневого зуба жесткости должны складываться следующим образом:

C = C 1 + C 2 + ....

Учитывая, что взаимодействие антагонистов можно воспринимать как последовательное соединение пружин (рис. 4), приходим к выводу, что в этом случае должны складываться величины, обратные жесткостям:

C = -CC- . C 1 + C 2

Формулы (4)–(6) позволяют вычислить жесткости всех пар антагонистов. Это, в свою очередь, позволяет определить, какая доля жевательной нагрузки приходится на каждую пару.

Пусть со стороны жевательной мускулатуры на нижнюю челюсть действует суммарный момент M . В момент, когда возникающие в периодонте зубов реактивные силы F_i уравновесят действие этого момента, будет выполняться уравнение равновесия

f Fl - M = 0,

ii i=i          2

где l_i – расстояния от пар зубов до линии, соединяющей височно-нижнечелюстные суставы (рис. 5), которую принимаем за ось вращения. В силу симметрии в формуле (7) рассматривается только половина пар антагонистов.

Пусть под действием момента M нижняя челюсть поворачивается относительно оси вращения на малый угол φ . Тогда силы взаимодействия пар антагонистов F_i можно найти по формуле

F = c_iu_i = c i ф l i .

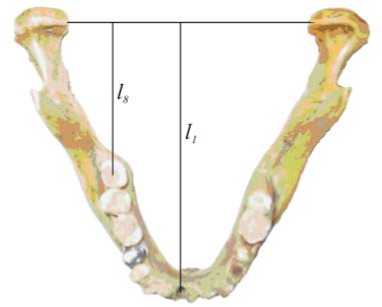
Рис. 5. Измерение расстояний от зубов до оси вращения на образце нижней челюсти

Подставляя (8) в (7), получаем выражение угла поворота нижней челюсти под действием момента M :

M

ф = ——

2 cl ²

ii i=1

Подставляя значение φ в (7), можем найти величины сил взаимодействия пар антагонистов F_i при заданном значении момента M .

Полную жевательную нагрузку F можно найти по формуле

F = 2ф£cili • i=1

Тогда доля жевательной нагрузки F_i ⁰ , приходящаяся на данную пару антагонистов, определяется выражением

0 Fi        cili не зависят от величины

F    p     8      •

^F 2 cl

Из полученной формулы видно, что значения F_i ⁰ развиваемого жевательной мускулатурой момента M .

Данные измерений

С целью проведения расчетов на имеющемся образце челюсти (см. рис. 5) были выполнены измерения радиусов корней зубов в области шейки r_i и расстояний от пар антагонистов до линии, соединяющей височно-нижнечелюстные суставы l_i .

Длины корней зубов   hi   и их количество ni (рис. 6) определялись по литературным данным [3].

Результаты измерений сведены в табл. 1.

Данные по периодонту, приведенные в табл. 2, были также взяты из литературных источников [2, 4].

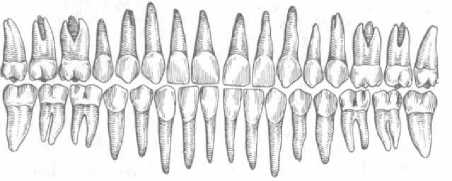
Рис. 6. Постоянные зубы верхней и нижней челюстей

Таблица 1

Значения параметров корней зубов верхней и нижней челюстей

Номер зуба	Название зуба	l , мм	Верхняя челюсть			Нижняя челюсть
			n	r , мм	h , мм	n	r , мм	h , мм
I	Центральный резец	92	1	2,5	12,5	1	1,5	12
II	Боковой резец	92	1	2	16,5	1	1,8	12
III	Клык	91	1	3	16,5	1	2,5	15
IV	Первый премоляр	86	2	2	12,5	1	2	14
V	Второй премоляр	81	1	2,5	12,5	1	2	14
VI	Первый моляр	70	3	2,5	13	2	2,3	13
VII	Второй моляр	61	3	2	13	2	2,2	13
VIII	Третий моляр	50	3	1,5	12	2	1,8	10

Таблица 2

Упругие свойства и геометрические параметры периодонта

Модуль упругости E , МПа	Коэффициент Пуассона ν	Размер периодонтальной щели δ , мм
		Верхняя челюсть	Нижняя челюсть
0,68	0,49	0,23	0,19

Таблица 3

Жесткость периодонта С , Н/мм

Номер зуба	I	II	III	IV	V	VI	VII	VIII
Верхняя челюсть	38,2	9,2	45,8	31,7	38,2	106	44,1	16,51
Нижняя челюсть	6,66	13,7	32,5	15,4	15,4	57,4	51,9	39,1
Общая жесткость	5,67	5,51	19	10,4	11	37,3	23,8	11,6

Таблица 4

Распределение жевательной нагрузки по зубному ряду при центральной окклюзии, % ______

Номер зуба	I	II	III	IV	V	VI	VII	VIII
По формуле (11)	2,8	2,7	9,3	4,8	4,7	14,3	8	3,3
По Н.И. Агапову [1]	4	2	6	8	8	12	10	0

Результаты расчетов

Приведенные выше данные измерений были использованы для вычисления по формулам (4), (5) жесткости периодонта зубов верхней и нижней челюсти, а затем по формуле (6) общей жесткости пары антагонистов. Результаты расчетов приведены в табл. 3.

Последние использовались для вычисления по формуле (11) доли жевательной нагрузки, приходящейся на данную пару антагонистов. Результаты приведены в табл. 4.

Если не рассматривать третий моляр и расставить пары антагонистов в порядке убывания их роли в акте жевания, то видим, что порядок, получающийся по формуле (11) и по Н.И.Агапову, практически совпадает. Исключением является клык. В первом случае он занимает второе место по степени влияния, а во втором случае лишь пятое место.

Представленная методика может быть использована для оценки распределения жевательной нагрузки по зубному ряду не только в случае отсутствия одного или нескольких зубов, как это делается при оценке жевательной эффективности по Н.И. Агапову, но и после того или иного ортопедического лечения.

Выводы

Получено аналитическое решение задачи по определению распределения жевательной нагрузки по зубному ряду. Решение использовано для оценки распределения жевательной нагрузки для конкретных параметров зубочелюстной системы. Предлагаемая методика может быть использована для оценки жевательной эффективности и в расчетах на прочность зубных коронок и зубных протезов.