Распределённая реакционная поверхность углеграфитовых объемно-пористых катодов как параметр оптимизации процесса металлизации композиционных и нанокомпозиционных материалов

Кошев А.Н., Кузина В.В. Распределенная реакционная поверхность углеграфитовых объемно пористых катодов как параметр оптимизации процесса металлизации композиционных и нанокомпозиционных материалов. Нанотехнологии в строительстве. 2025;17(2):119–131. – EDN: XWDYCA.

В различных областях промышленных производств высокотехнологичных изделий [1–9] используются композиционные материалы из углеродных волокнистых материалов (УВМ) с металлическим покрытием углеграфитовых нитей золотом, серебром, платиной, медью или другими металлами и их сплавами, выбранными с целью обеспечения заданных технологических требований.

Нанесение металлического покрытия на УВМ возможно различными методами, как химическими, так и механическими, однако наиболее эффективным методом металлизации твердой пористой основы представляется металлизация с использованием методов электролиза [10–14]. Гальваническая металлизация УВМ предпочтительна по ряду причин, основной из которых, безусловно, является возможность выбора режима электроосаждения: силы габаритного тока, скорости и направления протока

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ электролита, концентрации электроактивных веществ, конструкционных особенностей электролизера и прочих технологических условий. Выбор режимов электролиза, формы и материала катода, а также состава и концентрации электролита обуславливается требованиями к техническим параметрам создаваемого композиционного материала и технологическим параметрам процесса электроосаждения, к которым, в первую очередь, относятся равномерность распределения металла по толщине УВМ и интенсивность процесса осаждения.

Выполнить оптимизацию режимов электроосаждения и конструкционных особенностей электролизера с целью интенсификации металлизации и получения материалов с заданными свойствами невозможно без применения методов математического моделирования и расчета закономерностей электрохимических процессов и прогнозирования результатов электролиза [13]. Одной из основных характеристик, обеспечивающих значительную интенсификацию электроосаждения металла на УВМ в проточном трехмерном электроде (ПТЭ), представляется величина удельной реакционной поверхности электрода.

Электролиз металлов в электролизерах с ПТЭ осуществляется, как правило, из разбавленных рас- творов. Это позволяет использовать преимущества катодов из УВМ, такие как возможность вести процессы с высокой скоростью осаждения и достаточной степенью заполнения электрода металлом. Процесс металлизации УВМ лимитируется диффузией ионов к поверхности волокон. При этом толщина диффузионного слоя, ограничивающего скорость разряда ионов металла, для волокон диаметром 10 мкм принята равной 10–4 см [14, с. 19].

Очевидно, что при определении удельной реакционной поверхности УВМ должна учитываться не только общая боковая поверхность углеграфитовых волокон, но и те шероховатости поверхности (выступы, углубления и т.п.), размер которых в определяющих их высотах и глубинах составляет не менее толщины диффузионного слоя, т,е. величины, порядка 10–4 см.

В работах [14, 15] представлены результаты исследований, проведенных проф. В.К. Варенцовым с сотрудниками по определению величины S _v – реакционной поверхности УВМ при электроосаждении металлов в ПТЭ, лимитируемых диффузионной стадией гальванического процесса.

В табл. 1. приведены значения параметров некоторых нетканых и тканных УВМ: r – радиус волокна, S _v – удельная поверхность, определенная электро-

Таблица 1. Параметры углеродных волокнистых материалов

Материал	r , мкм	Sv , см–1	κ, См/см	ε
ВНГ-50	6,0	265	1,3/2,6	0,92
ВНГ-30	5,5	160	0,90/0,33	0,96
ВИНН-250	4,5	280	0,1/0,4	0,97
НТМ-200	5,0	216	0,07/0,4	0,96
НТМ-100	5,4	220	0,03/0,12	0,96
Мтилон	5,1	270	0,13/0,5	0,94
ВВП-66-95	4,7	255	0,006/0,05	0,96
ФРН	5,0	125	0,001/0,005	0,98
КНМ	6,1	160	0,009/0,03	0,98
ВИНН-150	5,0	220	0,05/0,16	0,92
КСС	4,5	–	0,1/0,2	0,89
Углен	5,1	240	0,05/0,13	0,95
Грален	4,9	260	0,1/0,4	0,96
НТ-1	6,2	165	0,001/0,02	0,90
НТ-2	6,2	165	0,003/0,014	0,90
АНМ	6,1	180	0,01/0,12	0,96
ТВШ	4,6	780	0,16/0,4	0,91
ТГН-2М	5,0	220	0,45/1,5	0,85
ЛВИК-95	6,0	270	0,26/0,87	0,83
ЛГ-50	3,8	150	0,02/0,09	0,76
ЛГ-30	3,7	180	0,64/2,1	0,78
ЛГ-10	3,4	170	0,44/1,4	0,77

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ химическим методом, κ – удельная электропроводность УВМ в свободном и сжатом в два раза состоянии (над чертой и под чертой, соответственно), ε – пористость УВМ [14, с. 22].

Результаты исследований, проведенных В.К. Варенцовым с сотрудниками и представленных в работе [14, с. 23], позволяют утверждать, что нетканые УВМ имеют существенно большую поверхность углеграфитовых волокон, на которой возможны электрохимические реакции, по сравнению с тканными УВМ.

Проведенная нами статистическая обработка данных из табл. 1 показывает, что наиболее значимыми факторами влияния на величину удельной реакционной поверхности S _v , являются радиус волокон r и пористость материала ε:

S _v = a ₀ + a _r r + a _ε ε + a _{r ε} r ε. (1)

На основании проведенных расчетов были определены коэффициенты регрессионной модели a ₀ , a _r , a _ε , a _{r ε} , при этом показано, что слагаемое a _{r ε} r ε в соотношении (1) является гораздо менее значимым в сравнении с первым и вторым слагаемыми. Следовательно, зависимость реакционной поверхности S _v как функции от параметров a ₀ , a _r , a _ε можно принять линейной:

S _v = 3066,93 – 574,911 r + 24,567ε. (2)

Построенная модель может использоваться для оценки удельной поверхности, если известны радиус волокон и пористость УВМ, при этом следует заметить, что они получены для 4,5 ≤ r ≤ 6,1 (мкм) и 92 ≤ ε ≤ 98%, поэтому их нельзя экстраполировать для r и ε, сильно выходящих за границы означенных интервалов. По этой же причине они могут оказаться малопригодными для определения удельной поверхности ПТЭ при электроосаждении металла, внутри пористого пространства, когда r и ε изменяются значительно.

В случае, когда радиус волокна УВМ, пористость материала и, как следствие, его удельная реакционная поверхность значительно меняются в процессе осаждения металла, необходимо учитывать эти изменения при математическом моделировании процесса электролиза.

Для нахождения зависимости удельной площади поверхности УВМ S _v от веса осадка металла M , в первом приближении, считалось, что осадок распределяется вдоль волокон равномерно. При известной пористости материала можно найти объем волокон, составляющих «таблетку» УВМ площадью 1 см²и толщиной 1 см, и определить n – число волокон в таблетке, полагая, что каждое из волокон представляет цилиндр известного радиуса r : n = (1–ε)/(π r ²).

При осаждении M граммов металла с плотностью q , г/см³, радиус волокон и пористость электрода становятся равными соответственно

• - ce

^M ~ Y "I" _ ' £M — £     ,(3)

nqnq а удельная поверхность

Sv = 2nrMn =----- /1 +      .(4)

Покажем величину изменения удельной реакционной поверхности от количества осажденного металла для r = 5·10^–4 см, ε = 0,95. Для этих значений можно принять n ≈ 6·10⁴. В начале процесса r _М = r , и из формулы (3) находим S _v = 200 см. Найдем S _v ^max , когда на ПТЭ осаждено максимально достигаемое на практике количество металла. Для золота это приблизительно M = 40 г на 1 г УВМ. Считая плотность углеграфита равной 1,6 г/см³ [16], нетрудно определить, что на рассматриваемый объем УВМ можно осадить 3,2 г металла. Для золота q = 19,6 г/см³. Подставляя эти данные в (3), найдем S _v ^max ≈ 413 см³. Таким образом определено, что в данном случае может происходить удвоение удельной поверхности ПТЭ за весь цикл осаждения металла из раствора. Очевидно, что при решении задач по определению технологических параметров процесса извлечения металлов на ПТЭ необходимо учитывать возможные изменения величин удельной поверхности, пористости, линейной скорости протока электролита и др. в динамике электролиза.

Для вычисления удельной реакционной поверхности S _v по уравнению (4) используем следующие рассуждения. Количество осажденного металла – ∆ M за время работы ПТЭ – ∆τ, в точке электрода – х , 0 ≤ x ≤ L , в сечении ПТЭ, площадью равной единице, определится соотношением: ∆M = [M(x,τ + ∆) – M(x,τ)]∆x ; концентрация ионов осаждаемого металла при протоке раствора электролита от точки x до точки x + ∆ x понизится на величину ∆ C = [ C ( x ,τ) – C ( x + ∆ x ,τ)]; концентрация ионов металла за единицу времени изменится на величину – ∆ Cm _v , а количество металла, осажденного в единичном сечении ПТЭ в точке x толщиной ∆ x , следовательно, будет равным ∆ Cm _v ∆τ.

Из очевидного соотношения [ M ( x ,τ + ∆τ) – M ( x ,τ)]∆x = ∆ Cm _v ∆ t , в пределах при ∆ x → 0 и ∆τ → 0, нетрудно получить формулу:

M ( x ,τ) = m _v dx ∫ ₀ ^τ (∂ C ( x , t )/∂ x ) dt .

M ( x ,τ) – количество металла в точке x за время τ – будем использовать при расчете удельной поверхности S _v ( x ,τ) по формуле (4).

Представленные сведения позволяют сделать вывод о том, что удельная реакционная поверхность ПТЭ должна рассматриваться как один из параметров, подлежащих оптимизации. Более того, воз-

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ можность подбирать материалы для формирования ПТЭ (см. табл. 1) позволяет рассматривать катоды с распределенной по толщине ТПЭ удельной реакционной поверхностью. Отметим также, что изменить значение Sv возможно за счет сжатия или растяжения выбранного материала катода.

МАТЕРИАЛЫ И МЕТОДЫ

Математическая модель

Исходя из электрохимической теории [17], поток заряженных частиц i -го сорта N _i в многокомпонентном электролите ( i = 1, …, n ) осуществляется под действием градиента потенциала электрического поля V E и протока электролита со скоростью v :

N i = z i µ i FC i V E + C _i v.

В этом соотношении z_i – заряд электроактивного компонента раствора; C_i – его концентрация; µ _i – подвижность.

В гомогенной среде справедливы условия материального баланса [17, 18], из которых следуют уравнения:

∂Ci /∂t = –(Ni),(6)

∂Ci /∂t = –(zi µi FCi VE + Ci v).(7)

Из (6) и (7) нетрудно получить уравнение (8):

г v                vг v i dt dx              ^ dx dx ^ . (8)

Необходимо отметить, что в преобразованиях уравнения (5) до системы дифференциальных уравнений (8) математическое моделирование проведено в соответствии с предположением о протекании реакции осаждения в каждой точке псевдогомогенного электродного пространства. Следовательно, концентрация ионов металла изменяется по мере движения электролита в объеме ПТЭ, то есть ∂ C_i /∂ x ≠ 0 в каждой точке с координатой x по толщине ПТЭ.

Моделируя изменение концентрации ионов металла по толщине ПТЭ ∂ C_i /∂ x с учетом зависимости удельной реакционной поверхности от координаты x по толщине электрода S = S_v ( x ), аналогично описанному в [18], получим соотношение в виде дифференциального уравнения, где в правой части присутствует неизвестная функция J_Si – распределенная плотность поляризующего тока:

dx \v\ziF $^l .                                    (9)

С учетом соотношения (9), уравнение (8) преобразуется к виду

F^ = ^-S_vWZJs^ . (10)

Считая, аналогично [18, 20], κ = 1/ρ = 1/(ρ _s +ρ _l ) и ρ _s = 1/κ _s , ρ _l = 1/κ _l , преобразуем уравнение (10):

^F£^zi^ = ^^ + S_VWYJs^^ . (11)

Система уравнений (9), (11) дополняется кинетическими уравнениями, связывающими J_Si и Е [18, 20]: _е^1р<^-_Чк1)/КТ __e(a_i--l)z_iF{E-^_Ri)IRT

J Site) =Jot — T^]^w=^rt^^  . (12)

Здесь φ _Ri – это равновесный потенциал i-й реакции.

Граничные и начальные условия для системы (9), (11), (12) можно представить следующими соотношениями:

∂ Ε /∂ n (τ,0) = J _g (τ) ρ _s ; ∂ E /∂ n (τ, l ) = –J _g (τ) ρ _l ;

C _i (τ,0) = C _{0 i} . (13)

Здесь J _g (τ) – габаритная плотность тока, подаваемого на электрод в момент времени τ, C _{0 i} – концентрация i -го электроактивного компонента в подаваемом в систему электролите. Отметим, что дифференциальное уравнение (11), в отличие от ранее используемых нами дифференциальных моделей, содержит в себе распределенную по толщине электрода величину удельной реакционной поверхности S ( x ). Такой подход влечет за собой необходимость существенной корректировки алгоритма и компьютерной программы расчета по модели (9), (11)–(13) в сторону усложнения.

На рис. 1. представлена схема ПТЭ с катодом из трех слоев УВМ различного типа.

Система уравнений (9), (11)–(13) позволяет рассчитывать распределенные по толщине ПТЭ неизвестные электрохимические функции: потенциал, плотность тока, концентрацию при распределенной, первоначально известной функции S _v ( x ) – удельной реакционной поверхности ПТЭ при извлечении металлов из многокомпонентного электролита. Для выяснения закономерностей и влияния S _v ( x ) на результирующие показатели процесса вполне допустимо исследовать поведение системы с ПТЭ для электролита с одним электроактивным компонентом, т.е. когда количество компонентов n = 1.

В качестве еще одного упрощения рассмотрим ситуацию, при которой C (τ, x ) представима в виде кусочно-постоянной функции от времени τ, то есть, когда весь интервал процесса может быть представлен объединением подинтервалов, в каждом из которых изменение концентрации от τ можно считать усредненно постоянным.

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

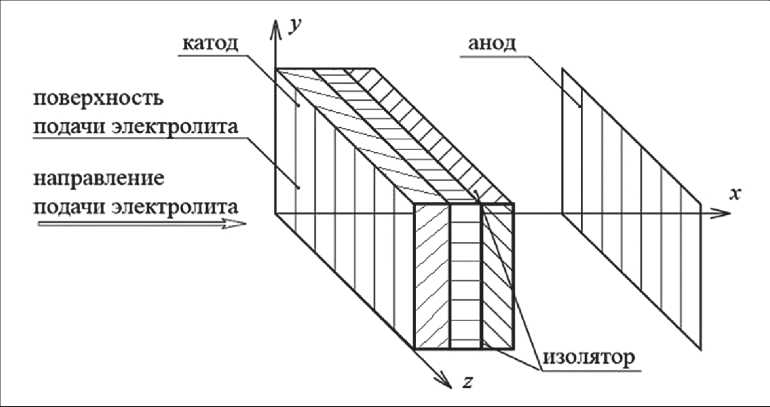
Рис. 1. Схема проточного трехмерного электрода с катодом из трех слоев УВМ

С учетом принятых упрощений рассматриваемая задача электролиза в ПТЭ запишется в следующей стационарной форме:

Уравнения (14)–(16) примут вид:

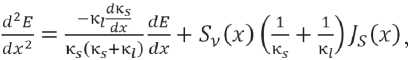
dC dx

dy _i / dx = f _i ( y ₁ , y ₂ , y ₃ , u ), i = 1, 2, 3                 (17)

VZF

JsM

T_x^=i^]^^       ,    (16)

J – общая электродная плотность тока.

С целью численной реализации модели (9), (11)– (13) разработан комплекс программ, при написании которого использовались алгоритмические языки программирования Delphi и Object Pascal.

Постановка задачи оптимизации

Рассмотрим задачу по расчету оптимального распределения удельной реакционной поверхности по толщине проточного объемно пористого электрода как задачу оптимального математического управления электрохимическим процессом за счет выбора оптимального управляющего воздействия u ( x ) = S _v ( x ). Обозначим:

^a RT’ ^ zFK_m’ ^ vzF’ &  \k_s⁺ kJ’

E =У1, -^— = У2= fi УУк У2’Уз,и); ax

= , dX ,У2 + u« - + -)jsM = dx ks(ks + Ki)          \ks KiJ

= Ь(У1>У2>Уз>и);

dy7 u(x)

УзМ = C(xf,— =--^JsM = f3jyi,y2,y3^j-

с граничными условиями:

y ₂ (0) = (1/κ _s ) J ; y ₂ ( L ) = (1/κ _l ) J ; y ₃ (0) = C ₀ .      (18)

Задача оптимального математического управления в общем случае состоит в определении расчетным путем управляющей вектор-функции u ( x ), обеспечивающей выполнение критерия наилучшей при данных условиях равномерности распределения плотности поляризующего тока или потенциала по толщине ПТЭ.

Критерий равномерности распределения функции J _S ( x ) можно сформулировать различными способами. В данной работе предлагается следующая форма:

Метод решения задачи

Для решения задачи оптимального математического управления (17)–(19) предлагается использовать принцип максимума Л. С. Понтрягина [21, 22]. Кроме очевидных преимуществ, заключающихся, например, в несложной алгоритмизации принципа максимума, необходимо отметить следующее обстоятельство. В работах [13, 20] были представлены исследования устойчивости системы дифференциальных уравнений (17), показано, что система является неустойчивой, к вариации начальных данных и функций в правой части системы. То есть, при проведении расчетов по моделирующим уравнениям, при значительных величинах толщины ПТЭ может возникнуть необходимость в применении регуляри-

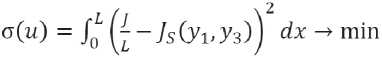
СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ зирующих методов. Известно, что принцип максимума Понтрягина обладает выраженными регуляри-зирующими свойствами [22].

Для реализации метода Л.С. Понтрягина систему (17)–(19) необходимо дополнить уравнением, соответствующим критерию оптимизации управления (19) и, сопряженной к уравнениям (17), системой дифференциальных уравнений относительно неизвестных функций ψ _i ( х ) i = 0, …, 2, связанных с основными функциями дифференциальных соотношений и задаваемыми методом начальными условиями:

dy ₀ / dx = (( J / L ) – J _S ( y ₁ , y ₃ ))² = f ₀ ( y ₁ , y ₃ , u );

y ₀ (0) = 0, (20)

d ψ _i / dx = –∑ _{j =0} ³ψ _j (∂ f _j /∂ y _i ), i = 0, ..., 3;

ψ ₀ (0) = 1; ψ ₁ ( L ) = ψ ₂ ( L ) = ψ ₃ ( L ) = 0. (21)

Правые части в уравнениях (21) для вычисления производных d ψ _i / dx не требуют сложных преобразований и могут быть представлены в аналитическом виде, несложном для алгоритмизации и программирования при вычислениях на ПЭВМ, однако результирующие формулы громоздки и в данной работе по этой причине не приводятся.

В соответствии с методом С.Л. Понтрягина, оптимальным управление u ( x ) будет в том и только в том случае, если его значения минимизируют так называемую функцию Гамильтона [21–23]:

H ( x , y ₀ ( x ), ..., y ₃ ( x ),ψ ₀ ( x ), ..., ψ ₃ ( x ), u ( x )) =

∑ _{i =0} ³ψ _i (x, y _i , u ) f _i ( x , ψ _i , u ). (22)

Минимизацию функции Гамильтона удобно осуществлять известным методом многомерного градиентного спуска. Предположим, что мы выполнили k итераций поиска, т.е. вычислили вектор u ^k ( x ) = ( u ₁ ^k , u ₂ ^k , ..., u _m ^k ).

Численные значения функций u ^k ( x ) позволяют решить систему (20)–(21), например, классическим методом Рунге–Кутты или любым другим методом [23]. Далее возвращаемся к вычислению u ^{k +1}( x ) посредством выполнения следующего шага минимизации функции Гамильтона и так до конца итерационного процесса, заканчивающегося, когда функция Гамильтона не меняется от итерации к итерации в пределах заданной точности.

Решение задачи оптимизации распределения управляющего воздействия u(x) = Sv(x) в некоторых специфических условиях.

При решении практических задач извлечения металла на ПТЭ и металлизации УВМ нередко можно принять следующие предположения и упрощения. Во-первых, можно считать, что изменение электропроводности УВМ по толщине ПТЭ в процессе элек-

тролиза незначительно, то есть d κ _s / dx ≈ 0, и первым слагаемым в уравнении (14) и последующими можно пренебречь. Во-вторых, за критерий равномерности распределения процесса электролиза по толщине ПТЭ принять равномерность распределения потенциала электрода.

Далее предположим, что задача по отысканию управляющего воздействия u ( x ) = S _v ( x ) решена, и распределение плотности тока электроосаждения металла близко к равномерному: J _S ( x ) = J _m . В этом случае можно считать, что распределение концентрации электроактивного вещества по толщине электрода близко к равномерному, и третьим уравнением в системе (17) можно пренебречь. Тогда задача (17)– (22) упрощается к виду:

dy ₀ / dx = | E ( x ) – E _m |;

dy ₁ / dx = y ₂ ;

dy ₂ / dx = u ( x )(1/κ _s + 1/κ _l ) J _m ;

> ψ0 (x) = 1; s m dψ1/dx = sign(E – Em);                        (23)

d ψ ₂ /d x = –ψ ₁ ;

y ₀ (0) = 0; y ₂ (0) = (1/κ _s ) J ; y ₂ ( L ) = (1/κ _l ) J ;

ψ ₀ (0) = 1; ψ ₁ ( L ) = ψ ₂ ( L ) = 0.

Для такой постановки задачи функция Гамильтона выглядит следующим образом:

H(x, y0, y1, y2, ψ0, ψ1, ψ2, u) = –|E(x) – Em| + + ψ1 y2 + ψ2 u(x)(1/κs + 1/κl)jm.(24)

Из системы уравнений (23) нетрудно определить:

ψ1 (x) = (x – L) sign(E – Em),(25)

ψ2 (x) = 1/2 (x – L)2 sign(E – Em)(26)

и, следовательно,

H = –| E ( x ) – E _m | + ( x – L ) sign( E – E _m ) y ₂ +

+ 1/2 (x – L)2 sign(E – Em) u(1/κs + 1/κl) Jm.(27)

Анализируя соотношение (27), нетрудно видеть, что управляющее воздействие u = S _v входит в выражение для функции Гамильтона линейно, и вычисление частной производной H по этой переменной, с последующим приравниванием этой производной нулю, к решению задачи не приводит. Однако заметим, что функция H = H ( u ) будет иметь минимум, когда третье слагаемое в выражении (27) будет минимальным. Учитывая известный U-образный вид функции распределения потенциала E ( x ) по толщине электрода [24], можно заключить, что в случае, когда E >  E _m , значение u ( x ) = S _v ( x ) должно быть минимально, а при E <  E _ср – максимально возможным.

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

Из этого следует, что предпочтительной с точки зрения равномерности распределения потенциала ПТЭ по толщине является ситуация, когда начальные слои УВМ имеют меньшую удельную реакционную поверхность, далее, в средней части электрода – большую и затем снова меньшую.

Пример решения задачи эффективного подбора слоев УВМ объемно пористого катода с целью улучшения равномерности распределения осажденного металла по толщине ПТЭ.

Рассмотрим результаты расчетного и экспериментального распределения осадка меди в ПТЭ толщиной 6 мм при использовании в качестве материала катода УВМ марки АМН (рис. 2) и ВНГ-50 (рис. 3), величины удельной реакционной поверхности которых значительно различаются: 180 см–1 и 265 см–1 соответственно. Необходимо заметить, что, как и ранее, все результаты экспериментальных исследований получены профессором В.К. Варенцовым и опубликованы, например, в работах [14, 20]. Состав электролита (г/л):

CuSO ₄ ·5H ₂ O – 170, H ₂ SO ₄ – 25, (NH ₄ ) ₂ SO ₄ – 80; удельная электропроводность 0,101 См/см; концентрация ионов меди 0,16 ±0,03 г/л. Осаждение меди осуществлялось при габаритной плотности тока 500 А/м². На рис. 2 и рис. 3 красные кусочно-линейные функции соответствуют эксперименту, синие – расчету при продолжительности электролиза, мин: а, б – 60, в, г – 180, – со скоростью протока электролита, см/с: а, в – 0,4, б, г – 1,0.

Результаты расчетов и экспериментальные данные, приведенные на рис. 2 и рис. 3, хорошо согласуются между собой. Можно также отметить, что при металлизации углеграфитового катода, составленного из УВМ марки ВНГ-50, общее количество осажденного металла превосходит общее количество металла, осажденного на катод, составленный из УВМ марки АМН, что объясняется лучшей удельной электропроводностью материала марки ВНГ-50. При этом нетрудно видеть, что распределение меди по толщине катода из УВМ марки АМН более равно-

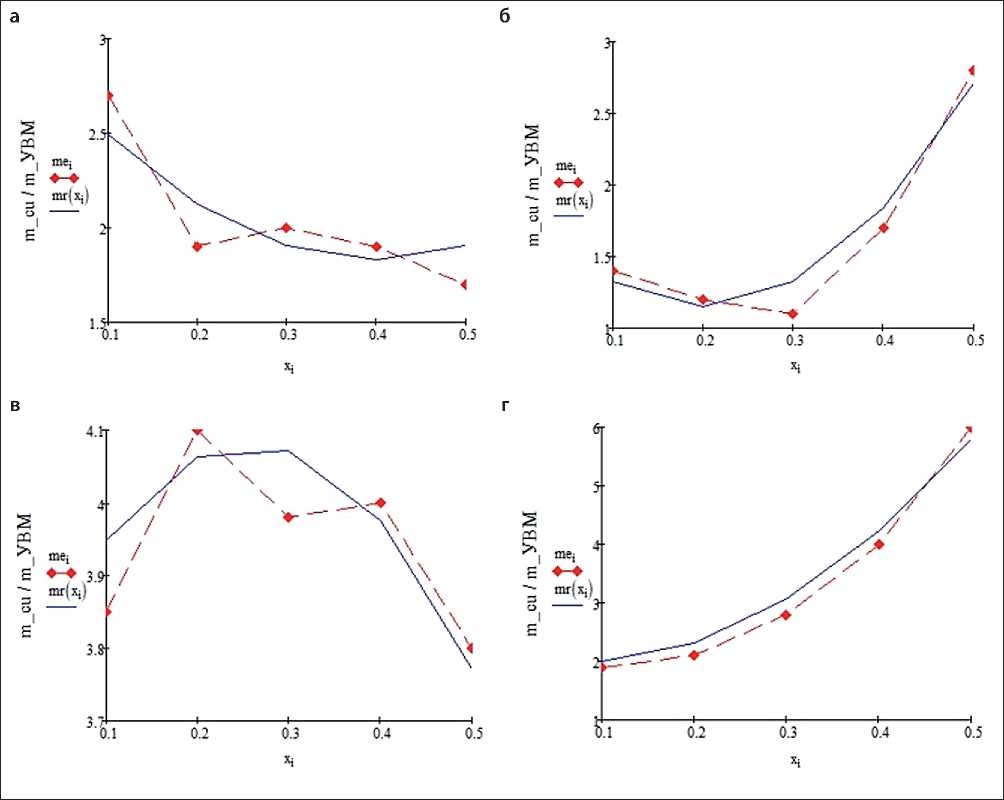
Рис. 2. Распределение металла по толщине УВМ марки АНМ

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

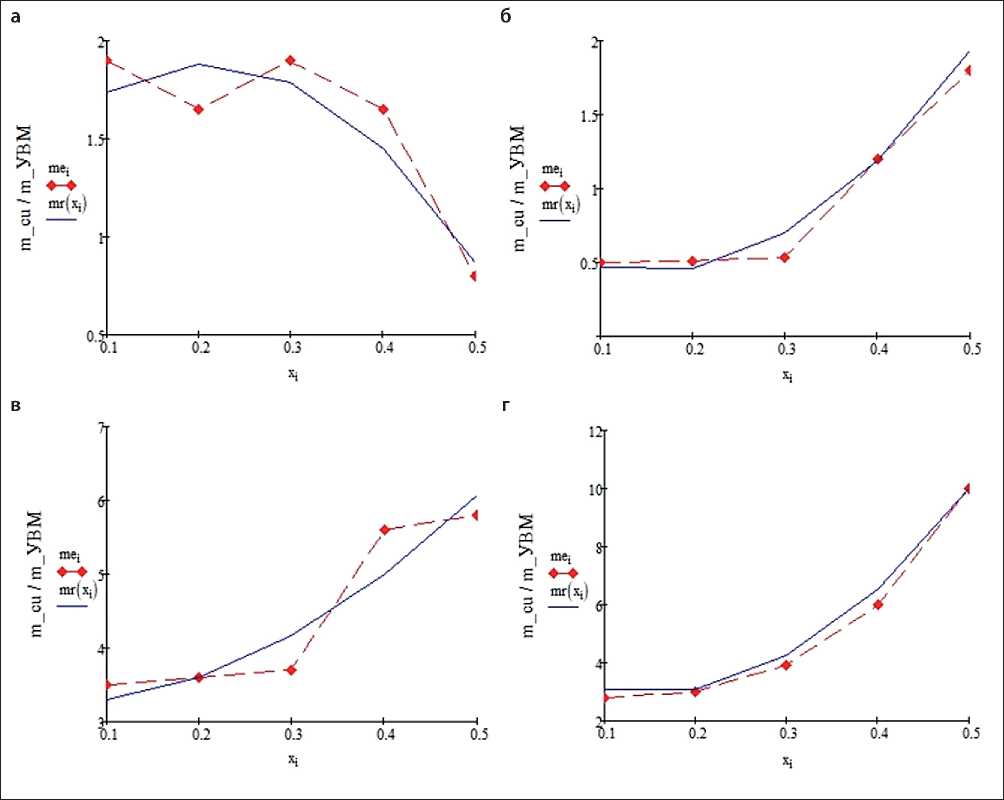
Рис. 3. Распределение металла по толщине УВМ марки ВНГ-50

мерное, чем распределение меди по толщине катода из УВМ марки ВНГ-50.

В соответствии с теоретическими выводами, приведенными выше, можно предположить, что для улучшения равномерности распределения медного покрытия ПТЭ можно было бы использовать объемно-пористый катод, составленный из трех слоев УВМ в следующей последовательности: первый слой – из УВМ марки АМН, второй слой – из УВМ марки ВНГ-50 и третий слой – опять из УВМ марки АМН.

На рис. 4 представлены расчетные данные распределения медного осадка в ПТЭ, состоящем из трех слоев УВМ: АМН; ВНГ-50; АМН.

Численная обработка результатов расчетов, приведенных на рис. 2–4, позволила составить табл. 2, данные которой отражают показатели равномерности распределения меди по толщине ПТЭ для рассмотренных условий, приведенных в подписях к означенным рисункам. Здесь max/min -показа- тель равномерности распределения осадка: max – наибольшая толщина осадка, min – минимальная толщина осадка, при различных условиях и конструкционных особенностях объемно пористого катода.

Основной вывод, который следует из анализа результатов расчетов наилучшего распределения меди по толщине проточного объемно пористого катода, заключается в том, что во всех сериях расчетов наилучший показатель равномерности распределения медного осадка в ПТЭ наблюдается в случае использования катода, составленного из трех слоев УВМ марок АМН, ВНГ-50, АМН, последовательно.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В работе предлагается подход к решению задачи улучшения равномерности металлического покрытия в объеме углеродного волокнистого материала, являющегося основой композиционного и нано-

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ

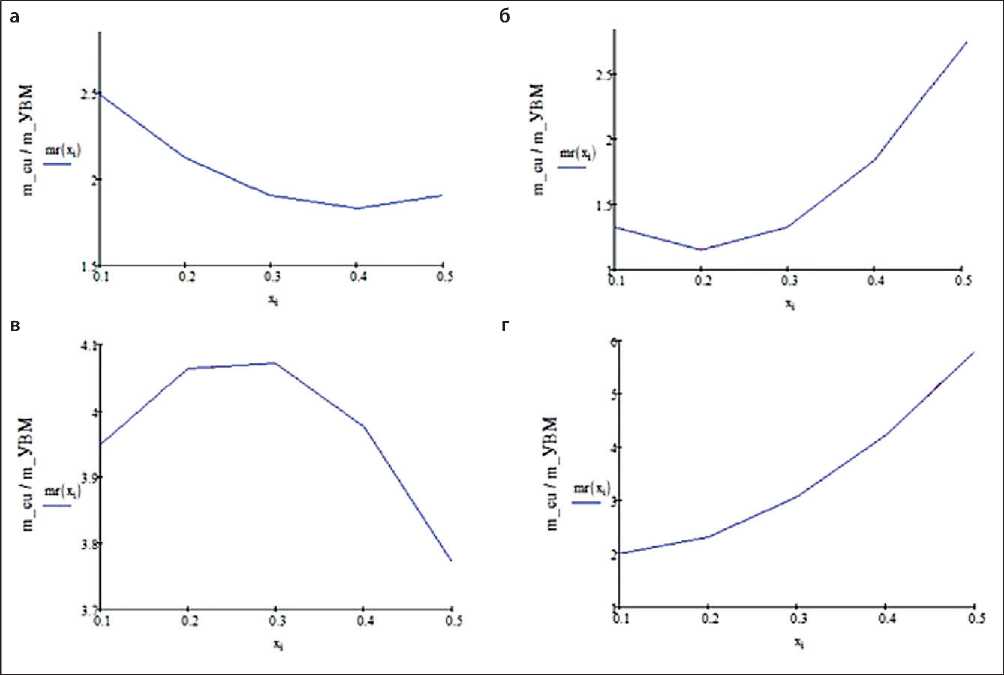
Рис. 4. Распределение медного осадка в ПТЭ из трех слоев УВМ – АМН; ВНГ; АМН: а – скорость протока электролита v = 0,4 см/с, время электролиза t = 60 с; б – v = 1 см/с, t = 60 с; в – v = 0,4 см/с, t = 180 с; г – v = 1 см/с, t = 180 с

Таблица 2. Значение показателя равномерности (max/min) распределения медного осадка по толщине ПТЭ

1-й слой УВМ	2-й слой УВМ	1-й слой УВМ	Скорость потока, v , см/с	Время электролиза, t , с	max/min
АМН	АМН	АМН	0,4	60	1,40
ВНГ-50	ВНГ-50	ВНГ-50	0,4	60	2,05
АМН	ВНГ-50	АМН	0,4	60	1,30
АМН	АМН	АМН	1,0	60	2,30
ВНГ-50	ВНГ-50	ВНГ-50	1,0	60	4,44
АМН	ВНГ-50	АМН	1,0	60	2,16
АМН	АМН	АМН	0,4	180	1,20
ВНГ-50	ВНГ-50	ВНГ-50	0,4	180	1,88
АМН	ВНГ-50	АМН	0,4	180	1,07
АМН	АМН	АМН	1,0	180	2,75
ВНГ-50	ВНГ-50	ВНГ-50	1,0	180	3,34
АМН	ВНГ-50	АМН	1,0	180	2,60

СТРОИТЕЛЬНОЕ МАТЕРИАЛОВЕДЕНИЕ композиционного материала, при гальванической металлизации УВМ за счет правильного формирования ПТЭ из слоев УВМ различных марок с разными величинами удельной реакционной поверхности.

Задача решается методом математического моделирования и последующего расчета с использованием классического принципа максимума Л.С. Понтрягина, позволяющего сформулировать и решить задачу оптимизации распределения потенциала, плотности тока и металлического осадка по толщине ПТЭ. При этом за управляющее воздействие принята распределенная удельная электропроводность электрода.

При разработке математических моделей, описывающих гальванические процессы в ПТЭ, учтено возможное изменение характерных электрохимических и технологических параметров, в том числе и удельной реакционной поверхности УВМ в процессе электролиза за счет изменения структуры УВМ при металлизации углеграфитовых нитей.

С использованием элементов регрессионного анализа построены и исследованы уравнения регрессии, связывающие значения удельной реакционной поверхности УВМ в зависимости от величины радиуса углеграфитового волокна и пористости углеграфитового материала.

Использование естественных упрощений и преобразований позволило привести математические описания к виду систем обыкновенных дифференциальных уравнений, что, в свою очередь, дало возможность представить и решить задачу оптимизации в аналитической форме и сформулировать некоторые практические рекомендации по использованию катодов из УВМ с распределенной реакционной поверхностью.

В качестве примеров решены практические задачи расчета распределения медного осадка при металлизации УВМ различных марок, показано, что использование катода из УВМ трех слоев обеспечивает более равномерное распределение металла по толщине электрода.

ЗАКЛЮЧЕНИЕ

Разработка математических моделей на основе современных положений электрохимической теории электроосаждения металлов на проточные углеграфитовые катоды и методов математического моделирования позволяет описывать процессы электролиза в ПТЭ в виде краевых задач математической физики, для решения которых необходимо использовать математический аппарат высокого уровня. В то же время разработанные математические модели позволяют формулировать задачи оптимизации процессов металлизации углеродных волокнистых материалов за счет оптимального распределения удельной реакционной поверхности по толщине проточного трехмерного электрода.

Математическое моделирование и численные методы расчета в рассматриваемом случае представляют собой эффективный научный метод для исследования и отыскания параметров оптимального управления электрохимическими процессами в пористой среде. Представленные методы и алгоритмы могут быть использованы как инструмент для теоретических исследований закономерностей электроосаждения металлов в ПТЭ и для численных расчетов оптимальных технологических параметров процесса электролиза и элементов конструкции электролизера.