Распространение электромагнитных ТЕ- и ТМ-волн в плоском волноводе, покрытом графеном, с учетом нелинейности

В настоящее время большое внимание уделяется изучению двумерных материалов и двумерных электронных компонентов. Среди прочих двумерных материалов особое место занимает графен, полученный экспериментально в 2004 г. Геймом и Новоселовым [1]. Графен представляет собой слой атомов углерода, образующих гексагональную решетку. Благодаря своей особой структуре графен обладает рядом уникальных электрических, тепловых, механических и оптических свойств, которые делают его весьма перспективным для различных применений [2]. Так, в фотонике и оптоэлектронике активно изучаются волноведущие структуры с графеном самых разных форм, начиная от простых прямоугольных и круглых цилиндрических волноводов и заканчивая волноводами весьма экзотических конфигураций, которые могут служить эффективными фотодетекторами, модуляторами, поляризаторами, сенсорами и т. д. [3].

Одним из наиболее важных свойств графена является его способность взаимодействовать с электромагнитными волнами в широком диапазоне частот, в частности в диапазоне частот от 0,1 до 10 ТГц. Как известно, терагерцовые технологии находят широкое применение в различных областях науки и техники. Так, например, они используются для химического и биологического зондирования, формирования изображений в ближней зоне, спектроскопии, телекоммуникации и т. д. Однако разработка эффективных электрических компонентов, способных обрабатывать и передавать ТГц-волны, до сих пор остается серьезной проблемой, тормозящей развитие ТГц-технологий. Считается, что графен, обладающий почти чисто мнимой поверхностной проводимостью в этом диапазоне частот, может быть полезен для решения указанной проблемы [4; 5].

В работах [6; 7] впервые было теоретически предсказано, что графен должен обладать силь-

LM^^e © Смирнов Ю.Г., Тихов С.В., 2023

ной кубической нелинейностью, обусловленной взаимодействием носителей заряда в графене с электромагнитным полем. С тех пор множество исследований выявили различные нелинейные свойства графена, включая насыщающееся поглощение и нелинейное преломление, генерацию высших гармоник и генерацию комбинационных гармоник. В частности, на технологически важных ТГц-частотах экспериментально были обнаружены насыщение поглощения в легированном графене [8] и генерация третьей гармоники [9].

В данной работе исследуется распространение монохроматических терагерцовых ТЕ- и ТМ-поляризованных волн в плоском диэлектрическом слое, покрытом с одной стороны слоем графена. Как известно, волноводные свойства графен-ин-тегрированных структур имеют большое значение для различных приложений и исследовались многими авторами [10–16]. Так, в работах [10–12] изучалась возможность распространения ТЕ- и ТМ-поляризованных волн, локализованных на слое графена, с дисперсией в терагерцовом диапазоне электромагнитного излучения. Распространение электромагнитных волн, локализованных в плоской структуре, образованной двумя графеновыми слоями и разделяющим их тонким слоем диэлектрика, рассматривалось в работах [13–15]. В работе [16] авторы исследуют распространение электромагнитных волн в структуре, состоящей из набора чередующихся слоев диэлектрика и графена.

Настоящая работа имеет следующую важную особенность. Мы учитываем нелинейное взаимодействие графена с электромагнитной волной. Точнее, мы предполагаем, что проводимость графена представляет собой сумму двух членов: первый - константа, а второй зависит от квадрата модуля тангенциальной составляющей электрического поля. Такая нелинейность отвечает так называемым эффектам самовоздействия в графене. Другие нелинейные эффекты, такие как генерация высших гармоник, в нашем исследовании не рассматриваются. В работе получено дисперсионное уравнение, позволяющее для волновода с заданными характеристиками определить его постоянные распространения. Следует отметить, что для получения дисперсионного уравнения в явном виде мы вынуждены наложить некоторые ограничения на проводимость графена, которые более подробно обсуждаются ниже. Тем не менее дисперсионное уравнение, записанное в явном виде, является важным результатом. Исследуя это уравнение численно или аналитически, можно определить свойства рассматриваемой волноведущей структуры.

1.    Электродинамическая постановка задачи

Рассмотрим монохроматические ТЕ- и ТМ-поляризованные электромагнитные волны

( E , H ) e i ^Y z ^- i ^to t ,

где го есть круговая частота; у - волновое число (постоянная распространения); E и H есть комплексные амплитуды (причем компоненты векторов E , H зависят лишь от одной (поперечной) пространственной координаты x ), распространяющиеся в плоском диэлектрическом волноводе S = = {( x , z ) е К ² : 0 <  x <  h }, расположенном между двумя полупространствами x < 0 и x >  h . На границе x = h волновода находится слой графена.

Волновод S заполнен однородной изотропной средой, характеризующейся постоянной диэлектрической проницаемостью S 2 . Полупространства x < 0 и x >  h заполнены однородными изотропными средами, которые характеризуются постоянными диэлектрическими проницаемо-стями £ 1 и S 3 соответственно, причем 1 < £ 1 < < £ 3 < S 2 . Всюду магнитная проницаемость ц = ц ₀ , где Ц о есть магнитная постоянная.

Комплексные амплитуды E, H удовлетворяет уравнениям Максвелла rotH = - itoSgsE, rotE = i гоцН, (2)

где S q есть диэлектрическая постоянная и

£1, x < h, s = <£2, 0 < x < h, I S3, x > h.

Амплитуды E, H удовлетворяют условию затухания на бесконечности. Касательная составляющая вектора E непрерывна на обеих границах волновода. Касательная составляющая вектора H непрерывна на границе x = 0, но терпит разрыв на границе x = h с графеном так, что справедлива формула n,

H ⁺ - H ^- ]

x = К

^G g E ^T l x = к ’

где скобка [ * , * ] обозначает векторное произведение, n = (1,0,0) есть единичный вектор нормали, направленный вдоль оси x , величины Н ⁺ и H ^- есть значения магнитного поля над и под поверхностью x = h соответственно, величина ст _g - поверхностная проводимость графена, Е _т - касательная составляющая электрического поля.

Проводимость графена стg описывается формулой ст g = ст(1) +ст(3)|Ет^, где ст(1) и ст(3) есть некоторые постоянные [6; 7].

Линейная часть ст(1) проводимости графена определяется по формуле ст(1) = i Im стint ra,                                                (3)

и ст _{int ra} = o _{int ra} ( to , ц c , T ) вычисляется по формуле

2ie2kbT ст™сra =                ln ля (to + iт )

2cosh

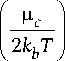
где e есть заряд электрона; k_b – постоянная Больцмана, Я есть приведенная постоянная Планка; ц c - химический потенциал; T - температура и т - время релаксации носителей заряда в графене [17; 18]. Подчеркнем, что используемая нами формула для линейной проводимости графена является «приближенной». Во-первых, она не содержит слагаемого, отвечающего межзонной проводимости в графене. Это оправдано при энергиях фотонов h to< 2 ц c , поскольку межзонные переходы в этом случае заблокированы в силу принципа запрета Паули [19]. Указанное неравенство, как правило, выполняется в терагерцовом диапазоне частот. Во-вторых, мы пренебрегаем действительной частью внутризонной проводимости графена или, другими словами, не учитываем поглощения в графене. Это допустимо в терагерцовом диапазоне частот, где графен обладает сильным плазмонным откликом и гораздо меньшими потерями. Кроме того, отметим, что мнимая часть внутри-зонной проводимости положительна в терагерцо-вом диапозоне частот.

Для вычисления нелинейного коэффициента ст(3) предлагаются разные формулы [6; 7; 20]. В данном исследовании мы будем использовать формулу, представленную в работе [7]. В соответствии с ней ст(3)= — i 3e vF ,                                             (4)

,

32to3 Я2ц c где Vf ~ c / 300 есть скорость Ферми в графене, а c есть скорость света в вакууме.

Задача заключается в нахождении таких значений волнового числа у = у' , при которых существует электромагнитное поле (1), удовлетворяющее системе уравнений Максвелла (2), условию затухания на бесконечности и всем приведенным выше условиям сопряжения. Числа у = у' называются постоянными распространения волновода.

Знание полного набора постоянных распространения необходимо при проектировании волноведущих структур.

Ниже будем использовать следующие обозначения:

• ⁶ 1 ( Y ) = V Y 2 — к оЧ, 6 2 ( Y ) = V k о ^е 2 — Y 2 ,               (5)

• 2.    ТЕ-волны

63(У) = д/у —kо s3 , где kо = to цоео.                                                  (6)

Пусть электромагитные волны (1) ТЕ-поляри-зованы, т. е. комлексные амлпитуды E и H имеют вид

E =(0,E _y ( x ),0), H =(H _x ( x ),0,H _z ( x )).

В этом случае задача о распространении электромагнитных волн сводится к задаче ^Te, ко-74                       |-------- торая заключается в нахождении у = у > к о J^, 74

таких, что существует решение Y = Y ( x ; у ) дифференциального уравнения

Y2 Y (x) - Y "(x ) = к 2Б2 Y (x), где Y(x):= Ey (x), удовлетворяющее краевым условиям

Y ' (о) -6 1 ( у ) Y (о) = о,                                       (7)

Y ' ( h ) + 6 ₃ ( у ) Y ( h ) = - 12С л ik _о ( ст ⁽¹⁾ +ст ⁽³⁾ Y ²( h )) Y ( h ), где 6 1 , 6 3 и к о определены в (5) и (6) соответственно.

Кроме того, мы вводим дополнительное условие для нахождения дискретного набора решений задачи, что соответствует физическому процессу распространения волн в волноведущих структурах. В качестве такого условия выберем

• Y (0) = A _TE,

где A _TE есть некоторая постоянная.

Задачу ^ Te можно отнести к специальному классу задач на собственные значения с некоторым дополнительным условием. Число у , являющееся решением задачи P TE , будем называть собственным значением задачи P TE , а функцию Y ( x ; у ) будем называть собственной функцией задачи P TE .

Поскольку условие (7) содержит кубический член Y ³ ( h ), то задача ^ Te является нелинейной. Она представляет новый класс нелиненейных задач с нелинейными граничными условиями.

Если в (7) положить ст(3) = о, то задача PTE вырождается в линейную задачу. Назовем ее зада- чей Те Подчеркнем, что условие (7) в линейной задаче тТЕ не требуется и потому может быть опущено.

Задача Т ^е так же, как и задача Т Те , описывает распространение монохроматической ТЕ-поляризованной волны в плоском диэлектрическом волноводе, покрытом слоем графена, который характеризуется линейной поверхностной проводимостью.

Решая представленное выше уравнения и используя краевые условия, получаем для задачи Tje дисперсионное уравнение вида ctg02 h = — —,                               (8)

0 2 Ф 2

где 02 показана в (3), а Ф1 = Ф1(y), Ф2 = Ф2(Y) определяются как ф1(Y) = -02 + 0103 -к0 Ы0i +

+ к ₀ a0 ₁ 0 2 ²( 0 2 sin² 0 2 h + 3 0 2 cos² 0 2 h ),

Ф ₂ ( Y ) = 0 1 +0 ₃ — k ₀ |^i| +

+ к 0 a0 22 (3 0 2 sin² 0 2 h + 0 2 cos² 0 2 h );

здесь ^ 1 = 120 ло ⁽¹⁾, a = |a ₃| A Te , o ₃ = 120 ло ⁽³⁾, где A _TE есть значение касательной компоненты вектора E на границе x = 0. Дисперсионное уравнение (8) позволяет для ТЕ-волны заданной частоты и волновода заданной толщины определить постоянные распространения волновода (прочие параметры также считаются фиксированными).

Касательная компонента электрического поля Y ( x ) вычисляется по формуле

Y ( x ) = А _Те 0 2¹ (0 1 sin 0 2 x + 0 2 cos 0 2 x ).

Задача Т Те исследована в работе [21], где получено дисперсионное уравнение, аналогичное уравнению (8). Однако в работе [21] дисперсионное уравнение записано несколько в ином виде, а именно, используя величины, нормированные на к о , см. формулу (6), что может быть неудобно для таких расчетов, в которых фиксирована толщина волновода и изменяется частота электромагнитной волны. Уравнение (8) этого недостатка не имеет.

Исследуя уравнение (8), можно получить достаточные условия для параметров волновода, при которых в нем могут распространяться монохроматические ТЕ-поляризованные электромагнитные волны. Следующие два утверждения дают такие условия.

Утверждение 1. Пусть n >0 есть некоторое целое число. Если параметры волновода S удовлетворяют условиям

^Б 3 > | О 1 |²

+Е 1 , h >

п ( n + 1) , - 1 k 0 ,

V ^Б 2 ^-Б 3

то существует по крайней мере n постоянных распространения y _n ^Г := (^ к о е ₃ , ^ к о Б 2 ), отвечающих n собственным модам волновода 2 .

Утверждение 2. Пусть n >0 есть некоторое целое число. Если параметры волновода S удовлет- воряют условиям

л ⁽ n + ^З^ | О 1 | — 1

^a >  | О 1 |, ^h >---- ^v —k 0 ,

J 3a^ - Б 1 )

то существует по крайней мере n постоянных распространения y _n ^Г := (^ к о s ₃ , ^к 0 Б 2 ), отвечающих n собственным модам волновода S .

Стоит отметить, что второе условие в последней формуле можно заменить более грубым, но в то же время и более простым неравенством вида h s 2 ^{n ( n + 1} к 0 ¹.

\ ^{3( б} 2 - ^Б 1 )

3.    ТМ-волны

Пусть электромагитные волны (1) ТМ-поляри-зованы, т. е. комлексные амлпитуды E и H имеют вид

E = (E x ( x ),0, E _z ( x )), H = (0, H y ( x ),0).

В этом случае задача о распространении электромагнитных волн сводится к задаче Т Тм , которая заключается в нахождении y = Y >  к о J^e 3 > таких, что существуют функции X = X ( x ; Y ), Z = Z ( x ; y ), удовлетворяющие системе уравнений | - Z " + y X ‘ = к 0 б ₂ Z ,

|-Z ' + yX = к0 Y-1s2 X, где X := iEx(x), Z := Ez (x), и краевым условиям

Б 2 0 1 ( Y ) X (0) -6 1 Y Z (0) = 0,                                 (9)

Б 2 0 ₃ ( Y ) X ( h ) + б ₃ Y Z ( h ) =

= -120л ik O1Y03( Y )(^(1) +о(3) Z 2( h)) Z (h), где 01(y), 03(Y) и ко определены выше.

Кроме того, мы вводим дополнительное условие для нахождения дискретного набора решений задачи, что соответствует физическому процессу распространения волн в волноведущих структурах. В качестве такого условия выберем

X (0) = ^1 А р _м, ε ₂

где А _тм есть некоторая постоянная.

Задачу Т ^м так же, как и задачу Т р _Е, можно отнести к специальному классу задач на собственные значения, где вводится некоторое дополнительное 74

условие. Число γ будем называть собственным 74                    74

значением задачи Т рм , а функции X ( x ; y ), Z ( x ; Y ) — собственными функциями задачи Т^м^-

Если в (9) положить о ⁽³⁾ = 0, то задача Т рм вырождается в линейную задачу, которую назовем задачей Т м - Заметим, что условие (9) в линейной задаче Т 0м не требуется и потому может быть опущено.

Задача Т м так же, как и задача Т ^м , описывает распространение монохроматической ТМ-поляризованной волны в плоском диэлектрическом волноводе, покрытом слоем графена, который харакетризуется линейной поверхностной проводимостью.

Решая указанную выше систему уравнений и используя краевые условия, получаем для задачи Трм дисперсионное уравнение вида ctg62 h = —^1—,                             (10)

ε ₂ θ ₂ ψ ₂

где ^ i = ^( Y ), V 2 = V 2 ( Y ) определяются как V i ( ^Y ) = = 1 ( k 0 = 3 ⁶ 2 ^- k 0 |^CT 1| 0 2 6 3 ) +

+ k ₀ в = ^{1 6} 2 ⁶ 3 ( е 2 б 2 sin² 6 2 h + 3 = 2 6 2 cos² 6 2 h )

- k 0 = 2 6X ,

V 2 ^{( Y} ) = ^k 0 = 1 ⁶ 3 ⁺⁶ 1 ( ^k 0 = 3 ^k 0 |^G 1| ⁶ 3 ) ⁺

+ k о в^{66 1} ( = 2 6 2 cos² 6 2 h + 3 e 2 6 2 sin² 6 2 h ) ;

ε ² ₂ γ ²

здесь в = 1^3]АTm, и Аtm - значение нормальной составляющей E слева от границы x = 0, другие величины определены выше.

Компоненты электрического поля X ( x ) и Z ( x ) определяются по формулам:

X ( x ) =

A

—^м ( 6 1 = 2 sin 6 2 x + = 1 6 2 cos 6 2 x ), ε ₂ θ ₂

A

Z ( x ) = ™( = 2 6 1 cos 6 2 x -= 1 6 2 sin 6 2 x ).

ε 2 γ

Исследуя уравнение (10), можно получить достаточные условия для параметров волновода, при которых в нем могут распространяться монохроматические ТМ-поляризованные электромагнит- ные волны. Действительно, имеют место утверждения 3 и 4.

Утверждение 3. Пусть n >0 есть некоторое целое число. Если параметры волновода Σ удовлет- воряют условиям:

ε ₃ ≥ | σ ₁ | ε ₂ -ε ₃ ,

( n + 1) π - 1 k ₀ , ε ₂ -ε ₃

то существует не менее n постоянных распространения y n ^£Г , отвечающих собственным модам волновода S .

Утверждение 4. Пусть n >0 есть некоторое целое число. Если параметры волновода Σ удовлетворяют условиям:

εβ

= 3> 7-1     , ^в- 1 ^ст 1^|>0 ,

β-|σ1 | h>

2 ε ₂ - ε ₃ (3 βε ₁ ² + ε ² ₂ | σ ₁ |) π ( n + 1) 3 βε ₁ ² ε ₂ - ε ₃ ( ε ² ₂ | σ ₁ | + 3 βε ₁ ²)

k

- 1

,

то существует по крайней мере n постоянных распространения y n ^£Г , отвечающих собственным модам волновода S .

4.    Численные результаты

Ниже представлены некоторые численные результаты.

В вычислениях мы использовали следующие значения для диэлектрических проницаемостей: = 1 =1, = 2 =11,7, = 3 =2,1025. Проницаемостью = 2 =11,7 обладает кремний (Si), а проницаемостью = 3 =2,1025 обладает диоксид кремния (SiO 2 ) [22; 23].

Для нахождения о ⁽¹⁾ и о ⁽³⁾ соответственно по формулам (3) и (4) использовались следующие параметры: ц c = 0,2 eV, T = 300 K, т = 10 ps. Время релаксации τ носителей заряда в графене выбрано в соответствии с [24].

На рис. 1–4 представлены дисперсионные кривые для рассматриваемого плоского волновода с графеновым покрытием. Как известно, дисперсионные кривые строятся как зависимость волнового числа (постоянной распространения) либо от частоты волны ω либо от толщины волновода h . Мы построили обе эти зависимости. На рис. 1 и 2 представлена зависимость γ ≡ γ ( ω ) при фиксированной толщине волновода, а на рис. 3 и 4 отражена зависимость γ ≡ γ ( h ) при фиксированной частоте электромагнитной волны.

Вертикальная прямая ω /2 π= 4 на рис. 1, 2 отвечает, соответственно, ТЕ- и ТМ-поляризованным волнам с частотой 4 ТГц. Вертикальная прямая

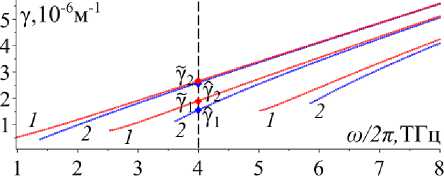
Рис. 1. Дисперсионные кривые задач Р °_Е ( 1 ) и ? Te ( 2 ) для волновода толщиной h = 20 мкм. Ромбами обозначены постоянные распространения Y 1 ~ 1,54, Y 2 ~ 2,59 (в нелинейном режиме) и Y 1 ~ 1,89, Y 2 ~ 2,64 (в линейном режиме) волновода

Fig. 1. Dispersion curves of problems P °_E ( 1 ) and P _TE ( 2 ) for a waveguide of thickness h = 20 µ m. Diamonds denote propagation constants Y 1 ~ 1,54, Y ₂ ~ 2,59 (in the nonlinear regime) and Y 1 « 1,89, Y 2 ~ 2,64 (in the linear one) of the waveguide

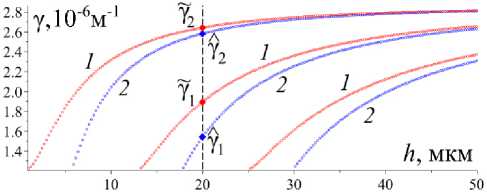
Рис. 3. Дисперсионные кривые задач т Т _Е ( 1 ) и ? Т _Е ( 2 ) для электромагнитной волны с частотой ω= 8 π ТГц. Ромбами обозначены постоянные распространения Y 1 ~ 1,54, Y 2 ~ 2,59 (в нелинейном режиме) и Y 1 ~ 1,89, Y 2 ~ 2,64 (в линейном режиме) волновода Fig. 3. Dispersion curves of problems P T _E ( 1 ) and ^ T _E ( 2 ) for an electromagnetic wave with frequency ω= 8 π THz. Diamonds denote propagation constants Y 1 ~ 1,54, Y ₂ ~ 2,59 (in the nonlinear regime) and Y 1 ~ 1,89, Y ₂ ~ 2,64 (in the linear one) of the waveguide

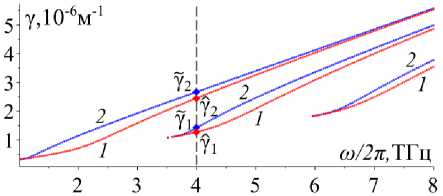
Рис. 2. Дисперсионные кривые задач pTm ( 1 ) и ^ Tm ( 2 ) для волновода толщиной h = 20 мкм. Ромбами обозначены постоянные распространения Y 1 ~ 1,4, Y 2 ~ 2,65 (в нелинейном режиме) и Y 1 ~ 1,25, Y 2 ~ 2,42 (в линейном режиме) волновода Fig. 2. Dispersion curves of problems t T_m ( 1 ) and P _TM ( 2 ) for a waveguide of thickness h = 20 µ m. Diamonds denote propagation constants Y 1 ~ 1,4, Y ₂ ~ 2,65 (in the nonlinear regime) and Y 1 « 1,25, Y 2 ~ 2,42 (in the linear one) of the waveguide

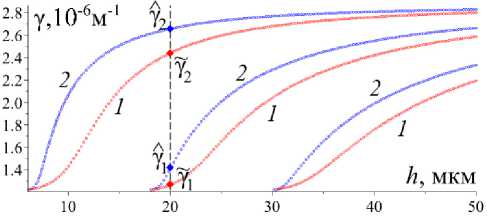
Рис. 4. Дисперсионные кривые задач ? Тм ( 1 ) и ? Тм ( 2 ) для электромагнитной волны с частотой ω= 8 π ТГц. Ромбами обозначены постоянные распространения Y 1 ~ 1,4, Y 2 ~ 2,65 (в нелинейном режиме) и Y 1 ~ 1,25, Y 2 ~ 2,42 (в линейном режиме) волновода

Fig. 4. Dispersion curves of problems ^ T _M ( 1 ) and P _TM ( 2 ) for an electromagnetic wave with frequency ω= 8 π THz. Diamonds denote propagation constants Y 1 ~ 1,4, Y ₂ ~ 2,65 (in the nonlinear regime) and Y 1 ~ 1,25, Y 2 ~ 2,42 (in the linear one) of the waveguide

h = 20 мкм на рис. 3, 4 соответствует волноводу толщиной 20 мкм. Точки пересечения дисперсионных кривых с этими прямыми, обозначенные на рисунках ромбами, являются постоянными распространения волновода.

На рис. 5–7 представлены компоненты электрического поля – функция E_y в случае ТЕ-по-ляризации и E x , E z в случае ТМ-поляризации -для постоянных распространения, отмеченных на рис. 1–4 ромбами.

Заключение

В данной работе, используя аналитический подход, исследовано распространение монохроматических ТЕ- и ТМ-поляризованных электромагнитных волн в плоском диэлектрическом слое, покрытом графеном. Важной особенностью данного исследования является учет кубической нелинейности графена, отвечающей так называемым эффектам самовоздействия, которые не влияют на частоту падающей электромагнитной волны.

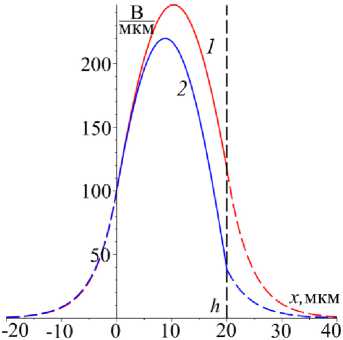
Рис. 5. Касательная компонента E_y электрического поля для постоянной распространения Y 1 ~ 1,54 ( 2 ) в нелинейном режиме (задача ^ Te ) и постоянной распространения Y 1 ~ 1,89 ( 1 ) в линейном режиме (задача ^ Te ), которые отмечены на рис. 1, 3 ромбами на кривых 1 и 2

Fig. 5. Tangential component E_y of electric field for propagation constant Y 1 ~ 1,54 ( 2 ) in the nonlinear regime (problem P _Te ) and propagation constant Y 1 ~ 1,89 ( 1 ) in the linear regime (problem ^ T_e ) which are denoted in figs. 1, 3 by diamonds on line 1 and 2

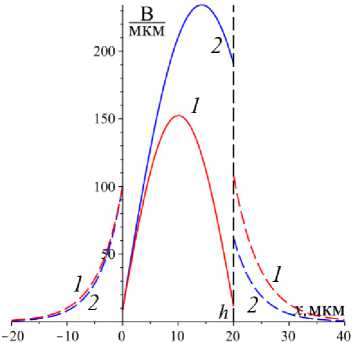
Рис. 6. Компонента iE_x электрического поля для постоянной распространения Y 2 ~ 2,65 ( 2 ) в нелинейном режиме (задача Tj_M ) и постоянной распространения Y 2 ~ 2,44 ( 1 ) в линейном режиме (задача 7 Т _м ), которые отмечены на рис. 2, 4 ромбами на кривых 1 и 2

Fig. 6. Component iE_x of the electric field for propagation constant Y 2 ~ 2,65 ( 2 ) in the nonlinear regime (problem P T _M ) and propagation constant Y 2 ~ 2,44 ( 1 ) in the linear regime (problem P _T ⁰ _M ) which are denoted in figs. 2, 4 by diamonds on line 1 and 2

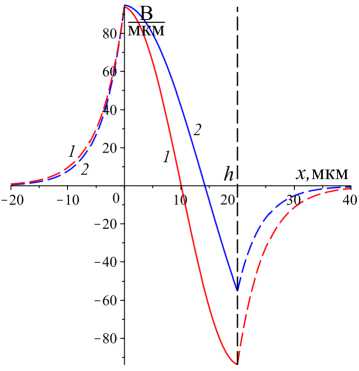
Рис. 7. Компонента E_z электрического поля для постоянной распространения Y 2 ~ 2,65 ( 2 ) в нелинейном режиме (задача Р _Тм ) и постоянной распространения Y 2 ~ 2,44 ( 1 ) в линейном режиме (задача Т Т °_м ), которые отмечены на рис. 2, 4 ромбами на кривых 1 и 2

Fig. 7. Component E_z of the electric field for propagation constant Y 2 ~ 2,65 ( 2 ) in the nonlinear regime (problem ^ T _M ) and propagation constant Y 2 ~ 2,44 ( 1 ) in the linear regime (problem T T 0_M) which are denoted in figs. 2, 4 by diamonds on line 1 and 2

В работе получены в явном виде пара дисперсионных уравнений (для ТЕ- и ТМ-волн), вполне описывающих волноводные свойства рассматриваемой структуры. При исследовании этих уравнений аналитически найдены условия на параметры волновода, обеспечивающие существование заданного числа волноводных мод.

Численные результаты, представленные в данной работе, дают некоторое представление о том, как нелинейность графена влияет на электромагнитные волны, распространяющиеся в структуре. Например, на рис. 1, 3 видно, что синие дисперсионные кривые задачи TTg (2) расположены ниже, чем красные дисперсионные кривые задачи ^Te (1). На рис. 2, 4 видно, что синие дисперсионные кривые задачи ТТм (2) расположены выше, чем красные дисперсионные кривые зада- чи ^Тм (1). Принимая во внимание связь между волновым числом и длиной волны, получаем, что в плоском диэлектрическом волноводе с графеновым покрытием в сильном нелинейном режиме распространяются ТЕ-волны с большей длиной волны и ТМ-волны с меньшей длиной волны по сравнению с ТЕ- и ТМ-волнами, распространяющимися в том же волноводе в линейном режиме. Кроме того, сильная нелинейность графена приводит к большей локализации электромагнитного поля внутри волновода, см. рис. 5–7.

Финансирование

Работа выполнена при поддержке Российского научного фонда [проект № 20-11- 20087; ].