Распространение нелинейных волн в соосных оболочках, заполненных вязкой жидкостью

1. Постановка задачи

В современной волновой динамике одним из важных направлений является изучение поведения волн деформаций в упругих оболочках. Так, в абсолютно жесткой трубе с круговым сечением ламинарное движение вязкой несжимаемой жидкости под действием гармонического поведения по времени перепада давления анализировалось в [1], а при пульсирующем движении вязкой жидкости в соосных упругих оболочках конечной длины — в [2, 3]. В условиях вибрации взаимодействие вязкой несжимаемой жидкости с упругими оболочками исследовалось в [4–7], а с учётом вращения жидкости — в [8–10]. Проблемы распространения волн в упругих и вязкоупругих тонкостенных конструкциях, в том числе в бесконечно длинных цилиндрических оболочках без взаимодействия с вязкой несжимаемой жидкостью, рассматривались в [11–14] с позиции теории солитонов.

Известны математические модели, учитывающие влияние вязкой несжимаемой жидкости на волновые процессы в бесконечно длинных геометрически и физически нелинейных оболочках [15-17]. При этом найдены эффекты влияния вязкой несжимаемой жидкости на поведение волны деформации в оболочке в зависимости от коэффициента Пуассона материала оболочки. В частности, при наличии жидкости в оболочке из неорганических материалов (различные трубопроводы в технологических сооружениях) выявлен экспоненциальный рост амплитуды волны. В случае органического материала (кровеносные сосуды) волна в жидкости быстро затухает.

Методом возмущений по малому параметру задачи получены математические модели волнового процесса в бесконечно длинных геометрически нелинейных соосных цилиндрических упругих оболочках [18, 19], которые описываются уравнениями динамики оболочек и несжимаемой вязкой жидкости, находящейся между ними, с соответствующими краевыми условиями, в виде системы обобщенных уравнений Кортевега де Вриза (КдВ). Показано, что волна деформаций во внешней оболочке приводит во внутренней оболочке к возникновению волны деформаций, которой в начальный момент времени не было. Происходит «перекачка энергии» (через слой жидкости) от внешней оболочки к внутренней, в результате этого во внешней оболочке имеет место немонотонное падение амплитуды волны, и, как следствие, немонотонное снижение скорости её распространения. При этом во внутренней оболочке амплитуда немонотонно увеличивается. С течением времени значения скоростей и амплитуд волн в оболочках выравниваются.

Решение поставленной в работе задачи для геометрически и физически нелинейных оболочек представляется актуальным и сложным и имеет важное значение для акустической диагностики и неразрушающего контроля материалов. Во многом интерес к подобным задачам инициирован необходимостью анализа упругих и динамических свойств нанообъектов, в частности, карбоновых нанотрубок.

Рассмотрим две соосные бесконечно длинные упругие оболочки (Рис. 1), между которыми находится вязкая несжимаемая жидкость. Ширина щели, занимаемой жидкостью — 5 , радиусы срединных

(индекс i = 1 относится к внешней оболочке,

поверхностей оболочек — R ⁽ ' ) , их толщины h 0 ' )

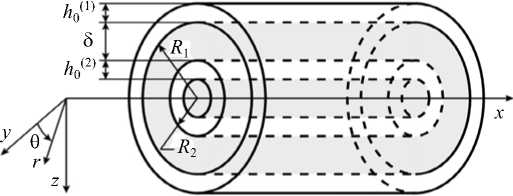
Рис. 1. Упругие бесконечно длинные соосные цилиндрические оболочки

индекс i = 2 — к внутренней); R 1 = R ⁽¹⁾ - h 01)/ 2 — внутренний радиус внешней оболочки; R ₂ = R ⁽²⁾ + h 0²⁾/ 2 — внешний радиус внутренней оболочки; R ₃ = R ⁽²⁾ - h 0²⁾/ 2 — внутренний радиус внутренней оболочки.

Уравнение движения несжимаемой вязкой жидкости и уравнение неразрывности в цилиндрических координатах ( r , 9 , x ) при осесимметричном течении имеют вид [21, 22]:

дVr  „ dV   дV  1 дp   (дV  1 дV дVV

,

+ Vr+ Vx+     = vl Г +r- +   rr- д t      д r      дx   p д r    ( д r2   r д r   дx2

д V „д V д V 1 д p   ( д ² V  1 д V д ² V )

+ Vr+ Vx+= vl      ++X I, д t      д r      дx   p дx    ( д r2   r д r   дx2

д V V д V _л

+   += д r r

При этом t — время; V x , V r — осевая и радиальная компоненты вектора скорости жидкости; p — плотность жидкости; v — кинематический коэффициент вязкости; p — давление в жидкости. Ось x совпадает с осью симметрии оболочек.

На границах оболочек и жидкости (Рис. 1) при r = R i - W ⁽ ' ) ( i = 1,2) выполняются условия прилипания жидкости [22]:

—= V x + U (О ^ V , - W 0) д Е с , д t              д x         д r

^JWl- = V + U (^ ^д2к - W (0 ^д2к . д t             дx        д r

Здесь: U^{(1 )} — упругое продольное перемещение i -й оболочки по оси x ; W^{(1 )} — прогиб оболочки (положительный к центру кривизны).

Запишем уравнения движения i -й цилиндрической оболочки в перемещениях для модели Киргофа-Лява в случае больших деформаций, считая материал оболочки нелинейно-упругим с кубической зависимостью интенсивности напряжений ст, от интенсивности деформаций e i [20]:

стi = E(') ei + m(') ei3, где E(1) — модуль Юнга, m(') — константа материала, которая определяется из опытов на сжатие или растяжение [23, 24] (далее полагается, что оболочки изготовлены из одного и того же материала):

Eh 0°

X

¹ ^ 0

L 4 m

x( 1 +--

I 3 E

uT

x

—

1                h ( ' )²

U ⁽' ⁾² ₊ ¹ W ⁽ ' ⁾² ₊ h O__ w < ' ⁾²

x 2 ' x 24 xx

W ⁽ i )   2

R ⁽ⁱ⁾

+ U ⁽ i ) W £ ^ ^x R ⁽ ' )

x

W⁽ⁱ⁾ '

^{Ц о}

- о h ⁽ ‘)U^{( 1 )} = -7 i ^p 0 h 0 U tt       ^q x

X

—

5 x ( i - 1),

Eh 0° ^{1 —} Ц 2

1                 1                    ⁽ i ⁾²

U (° + ¹ U (i)² + ¹ W ² + h ⁰— W 7' x 2 x 2 x 24 xx

W ⁽*) ]

^Ц о R l^X

4 m I

⁺ 3 E ।

W^{(i )}   2

W⁽i )

x

—

R w

R ⁽ⁱ⁾

—

R

⁽ i ⁾²                   jy⁽ i ⁾

¹ _ц и ² + ¹ _{ц o} w a² + h o- _Цо w ² — W- lx 2^ o x 2^ 0 x 24 ~ о xx R I

x

1 ± ⁴ m

3 E I

W^{(i )}   2

W ^{( i )} )

x

—

R ⁽ i )

R(i)

+ P o h 0° W^ = ( — 1 ) ' ^—1 q n + q n ( i — 1),

где p ₀ , p ₀ — плотность материала оболочки и коэффициент Пуассона; q x , q_n — напряжения, действующие со стороны жидкости, которая находится между оболочками; ^q x , ^q n — напряжения со стороны жидкости, заполняющей внутреннюю оболочку. Нижние индексы у перемещений обозначают соответствующие частные производные.

Напряжения, создаваемые наружным слоем жидкости, определяются по формулам:

X

х "1

qn

P_rr cos

— 1

■ n(l)

, n r

+ P_rx cos

— 1

■ n⁽' ) , i

,

V

V

r = R ' —W ⁽ i )

qx

P rx cos

— 1

■ n(l)

A

V

^P rr

d V

^— p + 2 p^v — r , d r

, n r

+ P. xx

. cos

— n⁽ ' ) , i

,

V

r = R i — W ^{( i )}

(5 V  d V |

P rx = P^vl 7 ⁺ I , V d r    d x 7

d r

^P xx

i d V_x ^— p + 2 pv — x . d x

В подходе Эйлера имеем

x

cos

cos

— 1

n

, n r

= R i

—

W w

x

V

N

,

cos

— n¹ ' ) , i

V

X

— n , n r

X

d W⁽i )

2XV² ,

cos

— n , i

—

R i — W ^{(i )} dW^l

d x ’

d W ⁽ⁱ⁾

—

d x

d W⁽i )

2X¹/² ’

d x

d x

r

| ^ = ( R i — W⁽ i ) ) 1 +

d W⁽ⁱ⁾

2XV2

d x

.

Здесь: n — нормаль к срединной поверхности i -й оболочки; nr, i — орты базиса в цилиндрической системе координат, центр которой расположен на оси симметрии оболочек. Если отнести напряжения к невозмущенной (внешней) поверхности наружной оболочки, то можно считать, что n = nr

( и cos -n, nr

= 1.

Напряжения q_x , q_n , возникающие от действия жидкости, которая находится во внутренней оболочке, определяются по тем же формулам (4), (5), но в них следует учитывать, что р — плотность заполняющей внутреннюю оболочку жидкости, а V — её коэффициент кинематической вязкости.

• 2.    Вывод уравнений динамики при наличии жидкостимежду оболочками и во внутренней оболочке

Принимая длину волны 1 за характерный размер и обозначая амплитуду продольного перемещения как u m и прогиб как w m , переходим к безразмерным переменным:

W^{( i )} = W m U 3° ,     U ^{( i )} = U m U f,     t '= c⁰- t ,     x '= x ,

Здесь c0 — скорость звука в оболочке. Полагаем:

— = Б <<  1,  — = O (б¹ *),  — = О( б ),

1            ’       1 ^v R     R ⁽■) ^л

E c 0 J A 2\"

V P o ( 1 -Цо )

w

^ = O( E ).

В этих переменных уравнения динамики оболочек (3) принимают вид:

1 Eh 0 i )

^{1 1 —ц} 0

—

u m u

Eh 0^

, ( i )

*

1 ^{1 x}

h 0 ^{i )0}

1 — ц 0\10 l ⁰

w m_u R ⁽ ‘ ) *

+ —

h ^{( i )0}

+

,( i )0

' 3

—

1 | U

о

u m

m

l

w m

1 R ^{( i )}

w

TU;

w m

l

о

u

( i )

'1 ” ” 3 x x

о

u

R ⁽ⁱ⁾

4 m

3 E

u

, ( ‘ ) о

*

’⁽ ) U 3

1 x ³

+

( i )0

+ —

wu

* *

3 x x

u

^Ц y ^U ₁

u m u

,*

1 I W m

о

l

w m

R ⁽ⁱ⁾

u

о

.* U

w ц0 —Uu.

⁰ R (i ) ■

^{+ Ц} 0 2

u

u

( i )

*

( i )

• 3

1 I U

w m u

R ⁽ ‘ i ■

, ( ‘ ) о

- *

3 x

,( i )0

' 3

, *

, *

xx

l

о

+ hL I w m 04 1¹

—

о

*

x

l

u

,( i )0

! * * 3 x x

, ( i ) c ° P0 ^h 0 у ^Um^U,

1 N

l

l

' 3 x*

^u m _u

l

**

1 t1

■ 1 x*

, 4 m

¹ ' 3 E

u m u

l

,*

—

u

( i )0

, *

^{+ Ц} 0 2

1 I W m

l

wu

lR(i)

U 3

U ' *

1 x

w

Ц,, m- U ⁽

⁰ R ( i ) ³

^— q x

—

4 m

3 E

<7 x ( i — 1),

+ -

1 1 u I                     I

m

l

u

, ( i )0

' 1 x *

+ —

1 I W m

l

u m

l

о

u

, ( i )0

*

1 x

—

u

, ( i ) 0

' 3 x*

+

w m _u R ⁽ ‘ ) *

A 0

, ( i )

' 3

u

.( i )0

' 3 x'

+

wu

1R ^{( i )}

U 3

u

, *

*

—

h Г I w_m

+ ц₀    —

⁰ 04 1²

l

c'L

⁺ w m P 0 ^h 0 i ) if ^U 3 ‘ f-

x

u

.( i )0

* *

3 x x

—

= q n ^(— 1 ) i ^{1 +} q n ⁽ i ^— 1).

Введём полухарактеристические (бегущие) координаты и растянутое время:

*          ,*,*

^ = x — Ct , T = Б t , где c — неизвестная безразмерная скорость волны. Тогда, разделив обе части первого из уравнений (6)

о 1 Ehf ^,(i)o1„ на у—°г = р0h0)c0 -, получим:

11 — ц0

um l

U^ )

wmj- _M( i

^Ц0   _D(o ^U 3

^U m ^R

+ 1 ^U m _,,( ‘ )0 ₊ w m "-,/ ‘ )0 । ^h I) ‘ ⁾⁰ w m   ‘ )0

I            U i      I U o I                  U cc

0 l   ^1S      U_ml ^3S    10 1² U_ml ^s

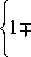
4 m I ^U m 1

3 E I l J

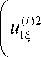
— wml

U m R^{( i )}

U /) U 3

+

w m 1²

U m r ^v)o

U 3 ^{i )0}

—

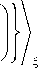
^U. ( c *U^

— 0 б cu^ T + б ⁰ u⁽ T ) ) =

—

1 ( q xi ) + q x ( i — 1))

⁽ i )c^{0 р} 0"0 ^c 0

Разделив обе части второго уравнения (6) на

, найдём:

um./ h?

l \ 12 l²

1   Eh 0° = Р о h 0i c 2

R ^{(i )} 1 -ц 0       R ^{( i )}

w m ^R _u(i ) u m i    ³⁵⁵

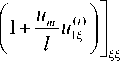
^P 0 ^u 12

+ u «

^U m ^R

—

¹ um_M'

^U 2

, ( i )2

1 w ²

P0-   m u

^{2 u} m ^l

( i )2

■ 35

_u 1 h Wm- ' 2 24 l² u_ml

u

( i ) 2

■ 355

4 f u

m

l

E

u ,

, ( i )2

' 15

—

w^ml u* i ) u ( ' u m R ^{1 5 3}

w m l ²

u m r ^{(i)2  3}

+

₊ R ^<0 J w m_u

l

l

' 35

⁽ i )

^{— u} 15 ^{+ p} 0

wml

^um^R(‘ ’

u

—

1 u

2 l

m u

( i )2

w² хи

: 15

—

m u

( i )2

+

w212 m

u m r ^{v)2 u 3}

(i)

+

W m R ^<0

l2

( c ² u

uml

( i )

' 355

—

Разложим упругие перемещения по степеням s

' 35

—

1 h 0 ^{, )2}

w2 m

2 24 l² u_ml

2 s cu 3 5T

2 ( i )

' 3tt

u

(i)2

■ 355

) = R^{(i )}

um l

4 mu 2 ^f (i)2 1 +— m u („)

3 El ² I ^{1 5}

—

( — 1Г q n + q n ( i — 1)

⁽ i) C2 ^p 0"0 c 0

u ^ ¹ ) = u ^) + s u^ i ) + ...,      u 3 i ) = u 30) + s u 31) + ... ,

подставим их в уравнения, разделим обе части уравнений на

_w L _u ( - ) _u v u_mR^{w 1 5 3}

+

^u„                                0

s = -m и, оставив члены при s

и s , придём

к выражениям:

^u 105    ^p 0

w m l

u m R ^(l)

^X| ^u ;0)5

—

^u 30)

wl

u m R

^u 30)

^{+ s}i ^u 1155

—

^—p 0

Ц 0

wl

u m R ^{( , )}

wl

u

( i )

- 31

1 u_m + — mu,

2 l s

( i )2

-105

4 m f u,

⁺ 3 E

m

l

2 Г

u

, ( i )3

-105

—

^{( 1 + p} 0 )

w m l

u m R ^{( , )}

11 ⁽) 11 ⁽) ^u105 ^u 30

X

u m R

u

( i )3

- 30

—

²u.(ⁱ^ c « 1055

—

s c ² u J i 5₅ + 2 s cu ⁽0 5_t

—

1 ²( q? + q x ( j — 1))

^u m ^p 0 h 0 c 0

,

II 11 ^{( 1} ) ^ 0 ^u105 ⁺

w m l

u m R

u

( i )

- 30

+ s

— I

■ Ц 0 ^u 115 +

w m l

u m R ^(l)

^u 31)

—

1 u_m , — u„ — u.

2 ⁰ l s ¹

u

, ( i ) 2

' 105

4 m

+т^

3 E s

u m

2 Г

l

Ц 0 ^u 105

—

( 1 <^U )

w m l

^u m ^{R (} i )

11 ⁽ ) ii⁽ ) ^u105^u 30

X

^x | ^u _H;

—

w m l

u m R °)

u

( i )

- 30

—

w m l

u m R^{( , )}

u

,( i )3

- 30

+

w m^{R (}‘ )

uml

c ^{2 u (}0)55

= R^{( i )} l

^{( —} 1 ) q n ⁺ q n ⁽ i ^— 1)

^u m ^p 0 ^h 0 c 0

Полагая коэффициенты при s0 нулевыми, получим систему уравнений:

и (i) ^u 1055

^— ^ 0

^w m ^l „( - ) u m R^{( 1 ) u 30 5}

—

c ²u⁽ⁱ) c « 1055

= 0,

( i ) + ^p 0 ^u 105 ⁺

wl

m ц)¹' umR ³⁰

= 0,

из которой следует:

^w m ^l _u ( - ) u m R ³⁰

^p 0 ^u 105 ,      ( 1 ^p 0 ^c ) ^u 1055   0.

Отсюда можем заключить, что u10 — это произвольная функция, а безразмерная скорость волны составляет c = 1— — ц0 , так как c2 =1 — ц0. Приравняем коэффициенты при s в правых и левых частях уравнений и учтём предыдущие результаты, тогда и 2м('') р0 u115

^{— р} 0

^w m ^l „( - )

D ( i ) ^u 31 ^u m ^R

^ 5

1 u_m m u

2 l s

( i )2 105

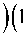
, ( i )³ 105

- 5

+

⁺²7 1 -ц 0 ^u 1⁽0)T5;у-ут⁽ q x¹ ) ⁺ <7 x ⁽ i ^—1)), ^{s u} m Р 0 ^h 0 ) c 0

Цо Цц

₊ wm=L_u «

UmR^ ³¹

—

1 и              1 R ( i )2

111 u m_ii )²+ i R h-M²^/ i )

2 ^ o l e ^u 10i ⁺ e l 2 ^B 0 (^{x   B} 0 ) ^и 10Щ

_R ( i ) l ^{( — 1 ) i 1} q n ⁺ q n ^{( i —} 1) ^e u m P o ^h 0 ^{i )} c 0

Умножим обе части второго уравнения на ц0 и продифференцируем по i . В результате получим:

^В 0 u lli

В о

wml

U m R ^G)

и ^w + И 31^ I +

А

1 ( Ч) T 4 m I u m I ( 1 — В 0 )( 1 + В 0 — В 0) U 0 A + 271—В 2 u »,

2 l e 3 E e ( l )         '             '

i

1 ²( q^ + q x ( i — 1)) , ^S u m ^p 0 ^h 0 c 0

^B 0 ^u11 i

„

■ ■ „ /?(i) u³¹i I ^Um^R      ii

₊ I,,²um„(О²

+ L 2 ^B0 l_e^i J

1 R⁾² 2Л 2 A (i)    _     R⁽ⁱ⁾l        G     —1 ⁵<n        П⁵qn j

Вычтем из первого уравнения второе и разделим обе части этого выражения на 2^1 — ц2 , тогда придём к системе вида:

„ (i)   . um u10iT+ le 2

и ⁱ) ^ui0i ^ui0ii

—

+¹

S

2^1 — Ц0 ^Sum P0^h0^Oc02

" ^{R w} Y            (i)     2m Г Um j²/         .

( l )      2     u10iiii + Eel l ) (1 B0 + B an u R(i)Гдqn( i—1-Ча ndqn qx + qx(i —1) — p0 "tI ^r(—1) + (i—1^г l (di               di

(i) 2 (i)

'' ' 1л

-i0i ^ui0ii

(i —1,2),

моделирующей движение волн в оболочках при наличии жидкости между ними и во внутренней оболочке.

В случае, когда жидкости в системе нет, правая часть уравнений становится равной нулю и получаются независимые модифицированные уравнения Кортевега де Вриза (МКдВ), а в отсутствие физической нелинейности — уравнения Кортевега де Вриза (КдВ) (при m = 0 ). Далее, чтобы определить в уравнениях (7) правую часть, необходимо решить уравнения гидродинамики для жидкости, заполняющей трубы кольцевого и кругового сечений.

• 3.    Определение напряжений в оболочках, возникающих от действия на них жидкости

  • 3.1.    Канал кольцевого сечения