Распространение волн во вращающемся упругом полупространстве

В технике находит применение немало машин, содержащих вращающиеся части: турбины, центрифуги и т.д. Во многих случаях желателен ультразвуковой неразрушающий контроль непосредственно во время эксплуатации, без остановки устройства. Несмотря на то, что используемые на практике ультразвуковые приборы кажутся, на первый взгляд, достаточно высокочастотными (1 - 5 мегагерц и выше), зачастую нельзя игнорировать влияние сил Кориолиса, чтобы пренебречь эффектами вращения. Так в работе [1] предложено ультразвуковое устройство (способ) для измерения давления в шинах, в [2] — для измерения трения во время вращения колеса, в [3] — для контроля качества бумажной массы, вращающейся на специальном барабане, в [4] — для определения дефектов на поверхности роликовых подшипников. Одновременно возрастает интерес к аппаратам, специально созданным для практического использования специфических эффектов, возникающих при распространении упругих волн во вращающейся среде. По-видимому, в [5] впервые предложено использовать для определения угловой скорости вращения изменения в скорости поверхностной волны, возникающие под влиянием силы Кориолиса. Из других работ по ультразвуковым датчикам вращения (гироскопам) отметим [6–10].

В работе [11], первой работе, в которой рассматривалось распространение волн во вращающемся изотропном упругом теле, отмечено, что волны во вращающейся среде становятся диспергирующими, однако исследование дисперсионных свойств распространяющихся волн не было выполнено. В работе [12] рассмотрен один частный случай распространения объемных волн перпендикулярно оси вращения. Для того же частного случая в [13] и [14] исследовалось распространение поверхностной волны в изотропном полупространстве, в [15] и [16] — в орторомбическом и моноклинном кристаллах соответственно (см. также работу [17]), в [18] — в кристалле с тетрагональной симметрией. В ряде работ [19–22] учитывалось влияние магнитного поля, теплопроводности и другое.

Для технических приложений интересен не только случай распространения упругих волн перпендикулярно оси вращения, но и самый общий случай распространения волн под произвольным углом.

Влияние вращения на волновые процессы достаточно многообразно. Оно приводит, во-первых, к повороту вектора поляризации у поперечной волны; во-вторых, — к видоизменению продольной волны, приобретающей под воздействием Кориолисовой силы поперечную составляющую; в-третьих, — к возникновению угла между направлениями распространения волны и потока энергии; и так далее.

В настоящей работе ограничимся рассмотрением влияния вращения преимущественно на фазовые и групповые скорости объемных и поверхностных волн, распространяющихся под углом к оси вращения. Заметим, что ранее распространение акустической волны в газе под углом к оси вращения рассматривалось в [23].

Объемные волны в равномерно вращающейся среде

Введем связанную со стационарно вращающейся упругой средой правую ортогональную декартову систему координат Ox 1 x 1 x 3 . Наряду с обозначением координат x j ( j = 1 , 2 , 3 ) будем использовать обозначения x , y , z . Во введенной неинерциальной системе координат уравнения движения упругой среды имеют вид [11]:

∂ u= 1 divσ +2[v,Ω]-[Ω,[Ω,u]]-[Ω,[Ω,r]], (1) ∂t2 ρ где u = (u1, u2, u3)T = (u, v, w)T — вектор перемещений; v = ∂u/∂t — скорость частиц; Ω — угловая скорость вращения среды; σ — тензор напряжений, связанный с деформациями обобщенным законом Гука σij = Cijkl uk,l ; Cijkl — тензор модулей упругости. Второе слагаемое в правой части (1) — Кориолисова сила, играющая ключевую роль в рассматриваемых ниже эффектах. В изотропной упругой среде динамическая часть уравнения (1) записывается как

^∂ _{∂ t} u ₂ = ( c ² _p - c_s ² )graddiv u + c_s ² ∆ u + 2[ v ,Ω] - [Ω,[Ω, u ]], (2)

где c ² _p = ( λ+ 2 µ )/ ρ , c_s ² = µ / ρ , λ и µ — модули упругости Ламе; ρ — плотность. Последний член в динамической части (2) уравнений движения, определяющий влияние центробежной силы, нередко опускают (например, в [13]).

Выберем ось Ox 3 системы координат так, чтобы она совпадала с осью вращения. Рассмотрим плоскую волну, распространяющуюся под углом χ к оси вращения в плоскости Ox 1 x 3 . Векторное уравнение (2) в развернутой форме с учетом того, что движение частиц происходит в плоскости Ox 1 x 3 , записывается в виде следующей системы:

- ( c Р - c p )( u + W z ) - c 2 (U xx + u ) - ^2QT ^v -^ u = 0, д t             д x                              д t

„ -c2(v + v) + 2^^u-^ v = 0, о t                       д t д2 W ,2     2. d ,               2                 „

TT ^{- (} c p ^- c s )^⁽ u x ⁺ w z ) ^- c s ⁽ w xx ^{+ W} ) = 0

д t              д z

Опуская промежуточные выкладки, приведем эту систему к одному уравнению для радиальной компоненты u вектора перемещений u:

д6u - Г ( c ² + 2 c_s ² )( д ² + д 2 ) - 2 Q? 1 д 4 и + t   p sxz     t

+ [ c 2 (2 c p + с 2 )( д 2 +д 2 )² -q. . c p - с 2 )( д 2 - 2 д 2 ) +п ⁴ ] д 2 u -

- c 2 c 4 ( д 2 + д 2 ) 3 u - n ² c ² Г ( c 2 + c ² ) д 2 + (3 c 2 + c ² » 2 1 д 2 u - ps x z             s p s x       p s z x

- 2 Q ² c 2 c, ² д 4 u - Q⁴ ( c ² д 2 + c 2 д 2 ) u = 0. ps z          s x p z

Здесь обозначено 3f = —, дх=— и так далее. Подставляя в (3) решение в виде 1 д tд d2

плоской волны с амплитудой й , распространяющейся под углом % к оси вращения

„ ik ( xsin X + z cos X-ct) u — u e,

получим уравнение для фазовой скорости c' = c / c s (ниже штрих опускаем):

(-1 + 4/т2 +1/т4)c6 +{2 + c2/cs2 - Г5 - c2/cs2 - 5(1 -c2/cs2)cos2 X1 /T2 -ps   psps

-[1 -(1 -cp Jc2)cos2 X]/T4}c4 +{-1 -2cp Jcp +

+ [1 - cp I cp - (1 - cp I cp) cos2 X] / T2} c2 + cp I cp = 0, где т = to/ Q — отношение частоты волны к частоте вращения.

В отличие от невращающейся безграничной изотропной упругой среды, где существуют две (продольная и сдвиговая) объемные волны со скоростями c p и c s , в рассматриваемом случае существуют три волны, которые обозначим через ql , m и qt . Эти волны являются диспергирующими, то есть их фазовые скорости ( c^ql , c^m и c^qt соответственно) зависят от частоты (Рис. 1). В пределе низкой частоты вращения т ^ ^ волна ql — это продольная волна c ql ^ c_p , а m и qt — поперечные волны разной поляризации. Условно назовем волну ql квазипродольной. Условность названия заключается в том, что с уменьшением отношения частот т вектор перемещений приобретает под воздействием Кориолисовой силы значительную поперечную компоненту, так что при т , близком к 2 и менее, волна становится ближе по свойствам к поперечной, а не к продольной волне. Фазовые скорости c^qt , c^m волн qt и m стремятся при т ^ ^ к скорости сдвиговой волны c s в невращающейся среде, причем c^m приближается к c s сверху, а c^qt — снизу. Волне qt соответствует в неподвижной среде

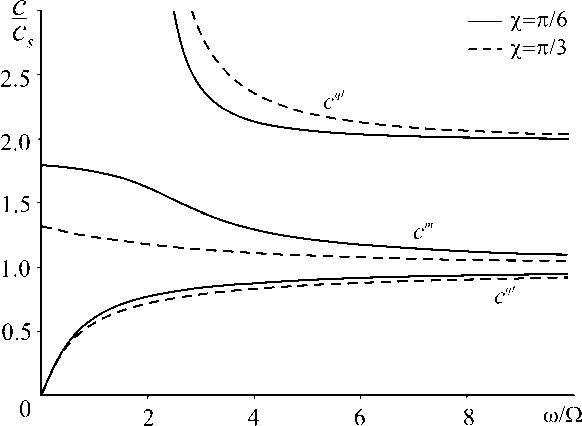
Рис. 1. Зависимости фазовых скоростей объемных волн от отношения частот т сдвиговая волна, у которой вектор перемещений перпендикулярен плоскости Oxz. Под воздействием Кориолисовой силы её вектор поляризации образует тупой угол с волновым вектором, фазовая скорость становится меньше cs, а при т ^ 0 она стремится к нулю. Графики фазовых скоростей показывают, что объемные упругие волны являются сильно диспергирующими в области низких т.

Угол % , под которым излучается волна, оказывает заметное влияние на дисперсионные характеристики (Рис. 1). На рисунке показаны зависимости фазовых скоростей от отношения частот т для двух значений угла (коэффициент Пуассона V = 0.33). Сплошные кривые соответствуют значению х = п / 6 , а штриховые — Х = п/ 3. При х = 0 вращение не оказывает никакого влияния на продольную волну. Отметим, что если пренебречь влиянием центробежной силы (последним членом в правой части уравнения (2)), то при х ^ 0 для квазипродольной волны ql обнаруживается критическая частота (частота запирания) щ c = 2 Q , ниже которой волна распространяться не может. При to <  2 Q могут распространяться только две квазипоперечные волны.

• 2. Поверхностная волна на границе равномерно вращающегося полупространства

Используем для волнового вектора k поверхностной волны следующее представление:

k = k ( m + p n )

где k — действительное, a p = p ‘ + ip " — комплексное числа; m — единичный вектор, задающий направление распространения поверхностной волны и лежащий в плоскости П , ограничивающей упругое тело; n — единичный вектор нормали к плоскости П , так что ( m , m ) = 1, ( m , n ) = 0, ( n , n ) = 1.

Следуя работам [16, 17], поверхностную волну представим как суперпозицию парциальных волн вида:

u ( x , t ) = a exp[ - i to t + ik ( m , x ) + ikp ( n , x )].

В отличие от предыдущего раздела, здесь для удобства выберем оси прямоугольной декартовой системы координат так, что x , = ( m , x ), x₃ = ( n , x ). Тогда выражение (6) запишем следующим образом

u ( x , t ) = a exp[ - i to t + ikx , + ikpx 3 ].

Поскольку из рассмотрения объемных волн видно, что исходно изотропная упругая среда, приведенная во вращение, приобретает черты анизотропной среды, то естественно обратиться к общему уравнению (1), учитывая, что тензор упругих модулей имеет вид C j _kl = X5 ij 5 _kl + ц ( 5 _ik 5 jl +5 il 5 j _k ), где 5 ij — дельта Кронекера. Как и ранее, в (1) опустим последний, не зависящий от времени член. Подставляя решение (6) в уравнения движения (1) и придерживаясь обозначений работы [24], получим

—                                2/

[( mm] -X E + p (^ mn] + num] ) + p (nn] ] a = 0 .

Здесь угловые скобки (в отличие от круглых, используемых для записи скалярного произведения) обозначают тензор ^ ab ^ = a j C ijkl b l . Также приняты обозначения:

E = (1 + t^{- 2} ) I - 2 i t 1 W + t ² WW T (верхний индекс T обозначает транспонирование);

^— x =

pto2 ,

k ^{2 ;}

t = to / Q ; I — единичная матрица. Матрица W j = Q j / Q имеет вид:

	Г 0	W 3	- W 2'
W =	- W 3	0	W ,
	< W 2	- W 1	0 J

Нетривиальность правого собственного вектора a обеспечивается условием у > '—'             /у > у >\ 2 / \

det[( mm] -X E + p (( mn] + num] ) + p (nn y] = 0

Нам интересны собственные значения p с Im( p ) >  0, поскольку амплитуда перемещений при распространении поверхностной волны должна убывать при удалении от свободной поверхности. Выражение для поверхностной волны как суперпозиции парциальных волн запишем в следующем виде:

u = ADq exp[ - i to t + ik ( m , x )] ,

где A = ( a 1 , a ₂, a ₃ ) ; D = diag( e^,kp i ^{( nx )} , e i ^kp 2 ^{( nx )} , e i ^kp 3 ^{( nx )} ); q — постоянный вектор.

Подставив (10) в граничные условия no = njоij = 0, получим где B = (bi,b2,Ьз),

^b a = {( nm ⁺ P a (nn)} a a ^{( a} = 1, ², ³⁾ •

По a суммирования нет.

Из условия нетривиальное™ вектора q следует уравнение det B = 0 • Из уравнений движения вытекает:

-1 X2^1

ba = Pa { ^ E — (mm) - Pa (mn/) aa

Опуская индекс a , уравнения (12), (13) объединим в одно матричное уравнение:

2и

Л E - (тт)

k - num)

0 If a 1

I 7k ^b 7

= P

f m^ 1 Y а ' k nut j v7k ь7

После небольших преобразований получим следующий вид уравнения (14):

N

a k b 7

f a 1

= p

k ^b 7

Здесь N =

f N X    N ² 1

k N ₃ + Л 2 Е N f J

где

— у          /     \ - 1 /      \ у /     \ - 1 у          /       \     /      \ /     \ - 1 /      \

N 1 =- nn] inm^ , N ₂ = nin] , N 3 =- mm ^ + ^ тп д пп) (nm ^ •

Обобщим уравнение (15) для любого целого n , включая отрицательные:

N ⁿ

a k b 7

= P n

f a 1

k ^b 7

Второе уравнение системы (16) для p = p 1 , p ₂, p 3 и n = 1 запишем в виде:

( N 3 +X 2 E ) A + N f B = B diag( P 1 , p 2 , p 3 ).                                          (17)

После умножения (17) слева на q ^T A ^T , справа на q и с учетом (11) получим:

a R ( N 3 +X ² E ) a _R = 0 ,                                                             (18)

где a _R = Aq — вектор поляризации на свободной поверхности (черта над символом используется для обозначения комплексного сопряжения). В общем случае для произвольного целого n имеем a R K ^{( n} ) a _R = 0, где K ⁽¹⁾ = N 3 + X E ,

K ⁽ 1) = ^гп) - Ппт( (( mm] -Я ² Е ) ¹ N ^ ¹ ( mn ) и так далее. Из теоремы Кэли-Гамильтона [25] следует, что из бхб матриц только пять матриц N n являются линейно независимыми. Для двухкомпонентной волны достаточно выбрать любые три целых числа п , например, п = - 1, 1 ,2.

Вектор a R возьмем в виде a R = (1, a ) T , тогда из (18) следует:

K (n ) а + K 2 n ) а + K ^ ) аа = K ^) .

В случае двухкомпонентной волны, распространяющейся вдоль поверхности вращающегося изотропного упругого полупространства, для элементов матриц K ⁽¹⁾ , K ^{( - 1)} , K ⁽²⁾ имеем следующие выражения: