Распространение звука в плазме самостоятельного газового разряда азотосодержащих газов

В последнее время наблюдается интерес к исследованиям различных гидродинамических явлений в плазме газового разряда. Это, в частности, связано с применением плазмы в аэродинамических и аэрокосмических приложениях [1, 2]. Эксперименты показывают, что прохождение звуковой волной плазменных образований может приводить к значительному изменению ее амплитуды [3, 4].

На наш взгляд, проблема взаимодействия акустических волн с плазмой молекулярных газов при таких условиях исследована недостаточно полно, особенно при значительном энерговкладе. Большинство работ по этой тематике посвящено изучению распространения акустических волн в плазме инертных газов при сравнительно малых энерговкладах [4]. В работе [5] теоретически рассматривалось взаимодействие акустических волн с плазмой молекулярных газов в условиях, когда время колебательной релаксации много больше периода колебаний. В то же время при значительных энер- говкладах в плазму, например, в воздухе, а также для низких частот порядка сотен Гц возможно обратное соотношение времени колебательной релаксации и периода колебаний. В свою очередь следует отметить, что у разных авторов по измерениям коэффициента усиления акустических колебаний в плазме азота и воздуха среди результатов имеются расхождения в несколько раз [4, 6].

Одним из основных выводов о механизмах взаимодействия акустических колебаний с плазмой самостоятельного разряда, сделанным авторами цитируемых работ, является то, что главную роль, по-видимому, играет, так называемый, Рэлеевский механизм [4, 7]. Суть его состоит в том, что если в среде с тепловыделением мощность объемного источника тепла зависит от плотности среды, то в такой среде будут наблюдаться усиление или ослабление звуковой волны в зависимости от сдвига фаз между пространственными зависимостями плотности среды и тепловыделением в волне. При этом, если электрическое поле в плазме и волновой вектор ортогональны, то волна будет ослабляться, если коллинеарны – то усиливаться [4, 8]. Нами рассмотрено взаимодействие плоской звуковой волны с неограниченной плазмой газового разряда в одномерной постановке. При этом исследован и случай молекулярных газов.

Вывод и решение уравнения распространения акустических колебаний в упругой среде с Рэлеевским механизмом тепловыделения

Будем полагать, что в отсутствии звуковой волны Рэлеевская среда представляет собой газ без объемных источников тепла, нагретый до некоторой температуры. Наличие звуковой волны приводит к неоднородности газа, что, в свою очередь, ведет к появлению тепловыделения. Пусть в единице объема газа выделяется мощность Q ( x , t ) ,

ω

—° = a . Тогда уравнение (1) можно переписать в ^k 0      ⁰

виде:

д [д2U д2U 1    ди дт [дт2   дz2 J 2b дz2’ (3)

где т = ю ₀ 1 ; z = k ₀ x — безразмерные время и ко-

ордината, соответственно;

b = Г -1 Р о       .

2 ю ₀ dp^p = ^{р 0}

Уравнение (3) в этих переменных имеет вид д2U д2U    дU

—2---2- = 2 b ---.

дт ²    д z ²        дт

где x , t – координата и время соответственно. Предположим также, что данная мощность в явном

Отметим, что условие применимости уравнения (5) для гармонической волны можно переписать в ином виде:

виде зависит только от плотности газа ρ , что со-

ответствует Рэлеевскому механизму влияния среды на акустическую волну. Используя нестационарную одномерную систему уравнений Эйлера, можно получить уравнение распространения звуковой

где

_v = Ю 1;

0   2 π

ν g

^V 0 >>  ^2V g ,

( У ^- 1 ) Р 0 dg l

2     dp^p = ^{р 0}

частота

волны в однородном газе с тепловыделением, зависящим от плотности:

нагрева [4].

Нетрудно убедиться непосредственной подстановкой, что частным решением уравнения (3) является:

д [д ² U д t 1 д t²

a

д2 U ] , d i dg\    д ² U

-   J = (у - 1) a о p^- p = p ——, (1)

д x²dp    д x ²

U ( x , t ) = exp[ ( ^ + i p )т - iz ] ,             (7)

где    β , µ   – некоторые параметры и

где a ₀ – скорость распространения возмущений бесконечно малой амплитуды; U – массовая скорость, вдоль которой распространяется волна; g = Q— ; p , P_o — плотность и давление газа в

γ P 0 ^{0 0}

отсутствии волны. Как видно, это уравнение третьего порядка, в отличие от обычного волнового уравнения второго порядка. При этом, как можно показать, при выполнении условия

Im в = Im p = 0 . Поскольку уравнение (3) является

линейным, то общее его решение есть сумма частных решений. Коэффициенты этого разложения находятся из начальных и граничных условий известными методами [9].

Таким образом, достаточно найти решение для случая гармонической волны. Подставляя (7) в (5) и приравнивая мнимые и реальные части полу-

d U

d t

t

>> ( у - 1) a о² dg |р = р j^ dt' d p    00 д x

,

(1а)

т.е. при малом тепловыделении, уравнение вивалентно

(1) эк-

чившегося равенства к нулю, получим:

г в 3 - 3 p ² в + в + 2 b = 0

[p(-p ² +з в ² +1 ) = 0 .

Система уравнений (8) имеет два типа решений:

Г p ² = 1 + 3 в ²

[ 4 в ³ + в - b = 0

2 д ² и д ² и , _n dg i a о       = .    ^- ( У ^- 1) р о-Т"

дx     д t              dp1

д U р=р 0 д t

p = 0

в ³ + в + 2 b = 0^.

с точностью до величин первого порядка малости dg по —j— | p=p . Введем пока произвольные парамет-

Очевидно, что решение (9) соответствует бегущей волне с амплитудой, зависящей от времени, решение (10) – стоячей волне с амплитудой, зависящей

ры ω ₀, k ₀ , имеющие размерности с^-1 и см^-1, соответственно, и удовлетворяющие соотношению

от времени.

Рассмотрим решение системы (9). Поскольку

по определению Im p = Im в = 0 , то, используя формулы Кардано [9], имеем:

ц = ± 71 + 3 в , в= A + B

( П i 23b+г +

у              V

релаксации - t_{vt 0} . Пусть при т >  0 плотность плазмы начинает меняться по некоторому закону р = р ( т ) , что вызывает изменения мощности тепловыделения и времени V - T релаксации τ _VT ( ρ ) . Тогда уравнение для энергии, накопленной

B =

( Г". Г b - . b ² + —

у

V

в колебательных состояниях ε_VT , запишется в

Различные знаки у параметра µ соответствуют

виде d^VT +^VT = gH (Р(т)) dr   TVT (р(т)X      ®0

волнам, бегущим в прямом и обратном направлениях, при этом знак величины β совпадает со зна-

ком параметра b . Формулы (11) для параметра β

имеют следующую асимптотику:

^в |b ^ 0 ^ ^b ; ^в _ь ^„

^

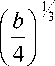
Здесь g_H ( ρ ( τ )) – объемная плотность мощности закачки энергии в колебательные состояния молекул азота в единицах р ₀ a ₀ ² = yP₀ ; £_VT измеряется также в этих единицах.

При этом очевидно, что искомое изменение мощности тепловыделения g и величина ε_VT связаны соотношением:

Аналогичным способом можно получить, что уравнение (5) имеет решение в виде бегущей волны (7)

с параметрами:

g = — — τ VT

ε VT 0 τ VT 0

ц 1 = ± V1 + 3 b² в = b

Вторая из формул (12) тождественно совпадает с формулами, полученными в работах [5, 10]. Как мы видели ранее, они верны только при выполнении неравенства (6). В общем же случае следует пользоваться формулами (11).

Можно показать, что решение уравнения (3), соответствующее системе (10), не имеет физического смысла.

Используя то, что в звуковой волне отклонения параметров газа от средних значений малы, получаем решение дифференциального уравнения (13) с начальными условиями ^£ VT I t = 0 = ^S VT 0 [9]:

^£ _VT ( t ) = exp"

1 Г dT'

--J-------f ^to 0 0 ^T VT

τ

1 ^£ VT 0

Вычисление параметра b для плазмы воздуха и азота

Как следует из определения величины b ,

поставленная задача сводится к расчету величины

dg dpp=р 0

1 dQ

γP ₀ dρ

, где Q – изменение коли-

Р = Р 0

чества тепла, выделяющегося в единице объема плазмы за секунду из-за наличия звуковой волны.

Известно, что в плазме азота и воздуха в рассматриваемых условиях практически вся энергия электронов расходуется на возбуждение колебательных степеней свободы молекул азота, которые затем релаксируют по колебательным состояниям в результате V - T процессов или на стенках, ограничивающих объем плазмы [11]. В соответствии с этим предположим, что в некоторый момент времени т = 0 однородная плазма обладает

плотностью ρ ₀ , в плазме существует стационарное распределение молекул азота по колебательным состояниям; энергия, накопленная в колебательных состояниях, равна ^ , и время V - T

1 Г            1

+--exp < — to 0 n          to 0

t'

J

dT I 7

----^ g H ( ^{T )d T} ^ ^T VT I

При условии, что амплитуда звуковой волны такова, что выполняется неравенство

^{2 n p -} P g|    ,

<< 1 ,

ω 0 τ VT 0    ρ 0

с использованием малости амплитуды звуковой волны можно получить следующий результат:

g(x) = ^ V^ τ VT

ε VT 0

τ VT 0

—

1  dτVT gH0

τ VT 0 d ρ

( P - P g ) + g H 0 exP « ω 0 τ VT 0

τ

^XJ ( P ^- P g ^exP «

1   dτ_VT

τ VT 0 d ρ

P = P 0

Отсюда видно,

—

p = P 0

τ

^X

t'

^to 0 ^T VT 0

^to 0 ^T VT 0

> dT

₊ ¹ dg_H g H 0 dρ

.

p = P 0 _

что для молекул газа предположе-

ние о том, что функция g ( τ ) в явном виде зависит

только от ρ ( τ ) , строго говоря, выполняется только в следующих случаях:

1) если to ₀ T VT 0 >> 1 , тогда

величины приводит к еще большему ускорению V - T процессов. Для вычисления величины

1 dT

τ VT 0

g ⁽ Р ) ~ - g H 0

1   d τ _VT

τ VT 0 d ρ

^{( Р - р} 0 ) ,

Р = Р 0

τ VT 0   dρ

= у запишем закон сохранения

Р = Р 0

2) если

2 π

ω 0 τ VT 0

>> 1 , то

exp

τ

– быстро

ω 0 τ VT 0

меняющаяся функция по сравнению с р - р ₀ , и

g < р ) • у- dρ

( ^{Р - Р} 0 ) .

Р = Р 0

В промежуточных случаях g ( τ ) зависит в явном виде не только от ρ ( τ ) , но и от τ , и, таким образом, уравнение распространения звуковой волны будет содержать член, пропорциональный

дg (Р(т),т )

дт

. Поскольку, как легко видеть,

Р = const

функция g ( τ ) , определяемая формулой (17), яв-

ляется монотонной функцией параметра ω ₀ τ _{VT 0} , то с достаточной степенью точности можно пользоваться любой интерполяционной формулой, которая в предельных случаях дает соотношения (18) и

д g

(19) и удовлетворяет равенству

дт

= 0 .

Р = const

Далее при проведении конкретных расчетов будет предложен один из вариантов такой интерполяционной формулы.

Таким образом, с использованием получен-

ных результатов (18) и (19), для параметра плазме воздуха и азота имеем:

b в

энергии для газа с дополнительным тепловыделением (теплопоглощением) в виде:

dT       T

— = ( y - 1)- + dρ      ρ

1 dQ

C_Vω ₀ ρ dρ

^где ,      Q H 0 y , Q HO = У ^gH 0 P 0 .

dρ

Как известно [12], случай колебательной релаксации молекул азота хорошо описывается формулой:

t _vt ^ —exp ^

B 0

Р     I T ^/3

Г ,

где B ₀ « 234,9 ; T выражено в ° К .

С учетом этого, используя соотношение (20), можно

получить:

_{1 +} ( у -1) B 0

1 +1/ у=- -1-2

ρ 0       B 0 Q H 0

13/

3 T 0 ⁴ ρ 0 C V ω 0

Теперь рассмотрим величину

dg _H d ρ

. При

Р = Р 0

давлениях газа в несколько десятков Торр и выше и

_ у 1 р0       1  dTVT b =          g н 0      з

2 ω 0     τ VT 0 d ρ

характерных частотах ω ₀ от нескольких десятков кГц и ниже частоты энергетической релаксации электронов в плазме воздуха и частота ионизации много выше ω ₀ [13]. Поэтому за время сжатия в

при ω ₀ τ _{VT 0}

Р = Р 0

>> 1

(19а)

и b = У - ¹ Р». dg H I    при

2 to ₀ Нр ^|р = ^{Р 0}

соответственно.

2 π

ω 0 τ VT 0

>> 1 ,

(19б)

Вычисление величин

1 dr

τ VTO

τ VT 0 dρ

звуковой волне успевают установиться стационарные значения электрического поля и концентрации электронов, соответствующие данной плотности нейтралов.

В силу этого, например, при рассмотрении случая, когда звуковая волна распространяется вдоль электрического поля, т.е. градиент плотности и электрическое поле коллинеарны, можно получить [14]

и

dgH dρ

dg _H         g _{H 0} jE

-----      = ----- = ------ .

^Н Р р = р ₀ р 0     У ^р р 0

для плазмы воздуха и азота

Р = Р 0

В случае же, когда звуковая волна распро-

Физические причины изменения времени V - T релаксации при изменении плотности состоят в том, что, во-первых, при увеличении плотности растет частота столкновений между молекулами, во-вторых, в сжатиях увеличивается темпе-

страняется в направлении, перпендикулярном электрическому полю, то, как отмечается в [14], поле в силу потенциальности будет сохраняться, а плотность тока – уменьшаться. Таким образом, в этом

случае

dgH

ратура, что из-за резкой зависимости τ_VT от этой

dρ

Р = Р 0

g_{H 0} ρ ₀

(22а)

Обсуждение полученных результатов и их сравнение с теоретическими и экспериментальными данными других авторов

Рассмотрим полученные результаты более подробно. Из первой формулы (11) следует, во-первых, что независимо от направления движения звуковой волны в плазме скорость распространения ее выше, чем в нейтральном газе, нагретом до той же температуры в ц > 1 раз. Коэффициент усиления (ослабления) волны с частотой ω0 , рассчитанный на единицу длины плазмы, связан с параметром β следующим соотношением:

K = ^ 0 в .                (23)

a ₀

В то же время по результатам других авторов [5, 10]:

K 1 = ^ 0 b . (24) a ₀

Эти формулы тождественно совпадают при выполнении неравенства (6) и дают разную зависимость от параметров плазмы в обратном случае. Например, коэффициент усиления (ослабления) K ₁ не зависит от частоты, в то время как величина K является растущей величиной ω ₀ . При этом

K 1 > K при любом о0. Графики зависимости a0K1 (ω0) и a0K(ω0) при различных параметрах X = bm0 приведены на рис. 1, 2. Зависимость a0K(ω0)(c-1)

a₀K₁( ω ₀ )(c^-1)

— - ^a 0 K ₁ ( _m„ ) — - a _o K( “ o> χ=50 c^-1

-■—■ -■ ■ । ggvw

ω0(c-1)

Рис.1. Зависимость величин a ₀ K , a ₀ K ₁ от круговой частоты звуковой волны при параметре х = 50 c ^{- 1}.

K ( ω ₀ ) качественно совпадает с экспериментальными данными [13], полученными для случая взаимодействия стоячих акустических волн с плазмой аргона при давлениях в десятки Торр и частотах до 1кГц. Отсутствие некоторых данных эксперимента в цитированной работе не позволяет провести количественно сравнение, однако тенденция роста коэффициента усиления звука с увеличением частоты звука при распространении его вдоль направле-

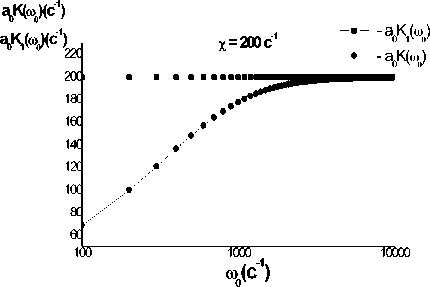
Рис. 2. То же, что и на рис. 1, но при х = 200 c ¹

ния электрического поля, зарегистрированная экспериментально авторами [13], свидетельствует о качественном согласии нашей теории с этими экспериментальными данными.

Покажем результаты вычисления величины dg dρ

Р = Р 0

Как видно из соотношений (18) и (19), при временах V - T релаксации много меньших периода звуковых колебаний изменение тепловыделения в плазме происходит за счет изменения мощности накачки энергии в колебания из-за изменения плотности газа. При обратном соотношении за малый период звуковых колебаний колебательная энергия не успевает отреагировать на изменение мощности накачки, и изменение тепловыделения происходит за счет того, что изменяется время

• τ VT .

Затем рассмотрим зависимость величин K y -1 jE и к, от параметра ---— = п в случае, ко-

• ¹                   2 γPa 0

гда звук усиливается. Нетрудно видеть, что, как следует из формул (22) и (24), K ₁ линейно растет с увеличением этого параметра, что совпадает с результатами [4]. Величина же K при малых η растет также линейно, однако затем асимптотиче- ¹

ски стремится к к ~ п ³ .

Необходимо отметить еще одно важное обстоятельство. Как уже отмечалось, время колебательной релаксации τVT в воздухе существенно зависит от температуры газа. Поскольку при увеличении параметра η растет энерговклад в плазму, то увеличивается температура газа, что приводит при фиксированной частоте ω0 к уменьшению па- раметра ω0τVT 0 и, в конечном счете, к смене механизма изменения тепловыделения в звуковой волне. Это обуславливает дополнительную зависимость величины K от параметра η и, как мы увидим в дальнейшем, может при низких частотах

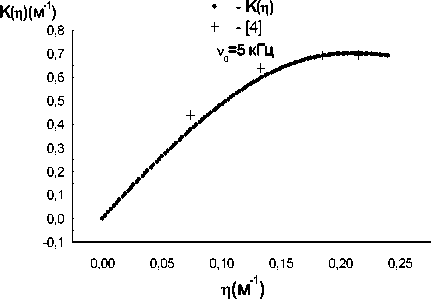
Рис. 3. Коэффициент усиления звуковой волны в плазме воздуха в условиях экспериментов работы [4]; кривая – расчет по разработанной теории, точки – результаты эксперимента.

ω ₀ приводить к немонотонной зависимости K ( η ) . На рис. 3 представлены результаты расчета величин K ( n ) для условий эксперимента работы [4] -

v 0 = 5 кГц , давление воздуха P 0 = 12,3 Торр и экспериментальные данные из этой же работы. Интерполяционная зависимость для параметра b

при различных значениях ω ₀ τ_{VT 0} выбиралась в виде

b = b₁ F 1 + b ₂ F 2 ,

где b ₁ и b ₂ определяются с использованием формул (21) и (22) соответственно;

предположении, что коэффициент теплопроводности пропорционален T . Авторы работы [4] расчеты коэффициентов ослабления звука проводили по формуле с точностью до обозначений, идентичной соотношению (24) и без учета механизма изменения энерговклада в молекулярных газах при росте температуры газа. В рамках этих допущений результаты эксперимента и расчеты авторов хорошо согласуются для инертных газов, когда величины параметра b малы и имеют значительные расхождения для воздуха. Как видно из данных рис. 3, построенная в настоящей работе теория позволяет хорошо описать данные эксперимента. В то же время в экспериментальной работе [6] при сле-

1                    f 1

F i =         ; F ² =         ;

1 + f 1         1 + f 1

(25а)

дующих условиях: P = 78 Торр , j — порядка не-

f 1 = — exp < 25,89

—

ω ₀

234,9 .

T У3

.

(25б)

мА сколькихединиц —-, f0 = 170Гц для тлеюще-см2

го разряда в азоте получено значение коэффициента усиления порядка 1,5 м ^{— 1} уже при параметре

Как видно из (25б), f ₁ пропорциональна величине

П порядка сотых м ¹ (а не десятых м ¹ , как в работе [4] и согласно расчетам настоящей работы). К сожалению, авторы не приводят данные эксперимента, которые не позволяют проанализировать причины столь большого расхождения экспериментальных результатов [4], расчетов по полученным формулам, и данных в работе [6].

На рис. 4 приведены зависимости величин K(п) и K 1(р) для различных частот о0 < 5 кГц и условий эксперимента работы [4]. Как и следует из качественного анализа полученных формул, величина K снижается при уменьшении ω0 . Кроме того, из этих же данных можно видеть, что зависимость K(п) при малых частотах является немонотонной, что связано, как уже отмечалось, со сменой механизма тепловыделения в звуковой волне.

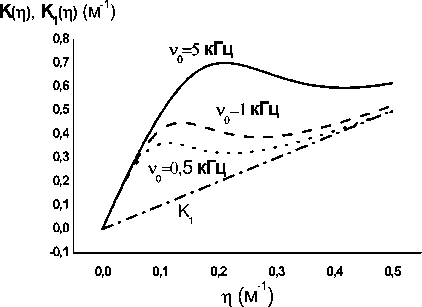
Рис. 4. То же, что и на рис. 3, но в более широком диапазоне величины энерговклада и различных частотах звука.

Построенная теория не учитывает потерь тепла в плазме за счет теплопроводности на стенки, ограничивающие плазму. Как показывают исследо- вания [4], учет этого явления приводит к незначительному уменьшению коэффициента усиления (ослабления) акустических волн в плазме.

Рассмотрим бесстеночный тлеющий разряд в воздухе (как наиболее перспективный в аэрокосмических приложениях) при значительных энерговкладах, а именно при следующих условиях: давление – от 10 до 100 Торр , плотность тока – от 5 до 100 мА / см ² . Для выполнения расчетов величины K необходимо знание температуры газа в области плазмы. Поскольку в настоящее время такие экспериментальные данные отсутствуют, то можно воспользоваться развитой в работе [15] теорией, где, в частности, рассчитывалось радиальное распределение температуры газа в бесстеночном разряде в воздухе.

Оценки и измерения газовой температуры в плазме воздуха при давлениях в десятки Торр и плотностях тока в десятки мА / см ² показывают ЕВ

[25], что при —* 10-------- [13] температура в

Р см Торр центре разряда превосходит величину порядка 1500 0К. Основываясь на данных [14] о скорости процессов V - T релаксации в воздухе, можно утверждать, что при частотах звука ω0 , меньших нескольких десятков тысяч с-1, выполняется соотношение (19б).

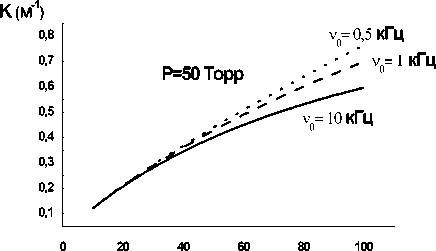
j ( мА/см² )

Рис. 5. Зависимость коэффициента усиления (ослабления) звука в бесстеночном разряде в воздухе от плотности тока.

На рис. 5 приведены зависимости коэффициента усиления (ослабления) звука от плотности тока при различных давлениях воздуха и частотах звука. При этом для воздуха принималось / * 1,4 • Из этих данных видно, что при увеличении плотности тока величина K растет независимо от частоты звука. Это, очевидно, вызвано увеличением энерговклада в плазму. На рис. 6 приведены результаты расчетов зависимости K ( P ) при различных плотностях тока. Видно, что величина коэффициента усиления (ослабления) в плазме слабо зависит от давления воздуха. Это объясняется тем,

K (м-1)

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

ν0=5 кГц j=100ì À/cì 2

j=50ì À/cì 2

j=20ì À/cì 2

10        20        30        40        50

Р (Торр)

Рис. 6. Зависимость коэффициента усиления (ослабления) звука в безстеночном разряде в воздухе от давления.

что при данных условиях в плазме энерговклад с ростом давления увеличивается очень медленно, что связано с медленным ростом электрического поля при увеличении давления из-за уменьшения плотности нейтралов в результате значительного неоднородного разогрева [15]. Скорость же звука в плазме растет с ростом давления, поскольку увеличивается температура газа. Как мы видели ранее, при увеличении скорости звука в плазме величина K падает. Указанные обстоятельства и приводят к незначительной зависимости величины K от давления.

Работа поддержана госконтрактом П585 на выполнение поисковых научно-исследовательских работ в рамках Федеральной целевой программы "Научные и научно-исследовательские кадры инновационной России" на 2009–2013 гг.