Рассеяние поля звукового пучка тонким слоем однородных включений

Электронный журнал «Техническая акустика»

Исследование закономерностей рассеяния акустических волн сосредоточенными неоднородностями среды, расположенными на некоторой поверхности, представляется актуальным для разработки новых подходов и технических средств дистанционного зондирования с целью определения свойств как одиночных рассеивателей, так и характеристик их пространственных распределений. Подобные задачи возникают при освоении океана, в частности океанского шельфа, где в качестве таких неоднородностей могут быть рассмотрены осадки произвольной природы, а также газовые пузырьки.

Представляет интерес совместный анализ амплитудных и фазовых характеристик рассеянного поля при произвольном расположении включений на некоторой поверхности. При этом практическое значение имеет случай, когда падающая на рассеивающую поверхность волна является звуковым пучком.

Примером практического использования результатов решения поставленной задачи является поиск и измерение характеристик загазованных участков морского дна для целей геологоразведки, мониторинга экологического состояния водоемов, при прокладке трассы подводных участков газопроводов и др.

Решение перечисленных задач требует разработки модели рассеяния акустических волн слоем малоразмерных объектов. Предложенная в настоящей статье модель основывается на результатах, полученных в работах [1–3]. В частности, в [2] показано, что морские донные осадки с одной стороны, в силу своей водонасыщенности, имеют практически те же акустические характеристики, что и вода; с другой стороны, осадочный слой обладает достаточной вязкостью, поэтому присутствующие в нем неоднородности, в частности газовые пузырьки, являются практически неподвижными. Приведенные факты позволяют в качестве одного из предположений при постановке задачи в простейшем случае представить газонасыщенный осадочный слой в виде равномерно распределенного на поверхности дна слоя однородных рассеивателей. Также в [2, 3] показано, что часть звуковых волн, проходящая через слой рассеивателей и достигающая твердой поверхности дна, поглощается и не оказывает существенного влияния на картину рассеянного поля, что повышает достоверность описания характеристик рассеивателей через параметры рассеянного поля. Для описания характера взаимодействия между рассеивателями в предлагаемой модели используется метод самосогласованного поля, особенности применения которого к средам, содержащим неоднородности, изложены в работе [4].

• 1.    ПОСТАНОВКА ЗАДАЧИ

• 2.    МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Пусть на плоской поверхности z = 0 произвольным образом распределены одинаковые рассеиватели. На плоскость z = 0 под углом 0 0 к нормали падает звуковая волна в форме осесимметричного продифрагировавшего гауссова звукового пучка, как показано на рис. 1. Необходимо определить амплитуду и фазу рассеянного поля в произвольной точке верхнего полупространства z >  0, их связь с параметрами падающей волны и характеристиками рассеивателей.

В пределах главного максимума характеристики направленности пучок представим квазиплоской волной с амплитудным распределением вдоль фронта. Тогда потенциал поля колебательной скорости падающей волны в произвольной точке M звукового пучка, рис. 1, можно записать в виде

^ i ( Г, R , t ) = ^ o , (- R ) ■ expt ( ^ t - kr ) ] ,

где о - круговая частота; t - время; к - волновой вектор; Г(x, y, z) - радиус-вектор точки наблюдения M ; T _{o i} ( R ) - множитель, учитывающий распределение амплитуды вдоль фронта волны; R – радиус-вектор отстояния точки M относительно оси пучка OL .

Координатные оси Ox и Oz декартовой системы развернем так, чтобы ось пучка OL оказалась в плоскости xOz . Тогда волновой вектор k будет иметь компоненты:

k = к ( - к ₀ sin 0 _o; 0; - к ₀ cos 0 _o ) ,

где к0 = к. Обозначим через г0 радиус-вектор точки K, которая является проекцией точки M на ось пучка, тогда r02 + R2 = r2. Выражая длину вектора r через скалярное произведение вектора Г(x, y, z) и единичного вектора (- к/к0), получим r0(x,z) = -(к/к0; г)= xsin00 + zcos00.

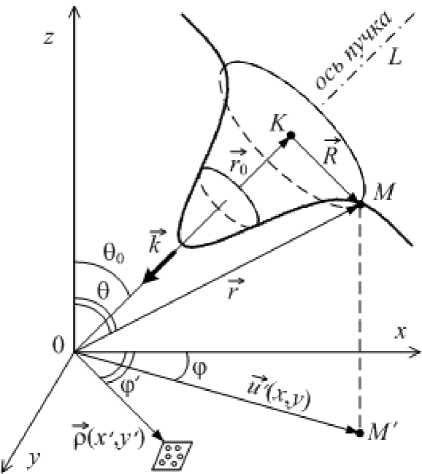
Рис. 1.

Геометрия задачи

Используя соотношения (2) и (3), получим выражение для R ² (квадрат модуля радиус-вектора отстояния):

R = r — ro = (x + y + z )—(xsin0o + zcosOo) = (x■ cosOo — z • sin0o) + y .        (4)

В гауссовом пучке амплитудный множитель в выражении падающей волны (1) имеет вид:

* o , ( R ) = A _oexp ( — R 21 R 02 ) .                                                               (5)

Здесь параметр R ₀ – ширина звукового пучка по уровню 1 e . С учетом (4), получим:

^ 0 , ^{( x}, y, ^z ) = A o^ex P

x ■ cos Q 0 - z ■ sin 0 0 ) + y

.

В плоскости расположения рассеивателей ( z = 0 ) выражение для потенциала примет вид:

% ( x , y , z = 0) = exp

(

- x

22  2

x ■ cos 0 o + y

R o 2        )

exp ( ''k 0 x ■ sin0_o ) .

В дальнейшем, не уменьшая общности, примем амплитуду падающей волны в выражении (7) равной единице, а временной множитель опустим.

Воспользуемся соотношением (7) для вывода выражения потенциала, создаваемого рассеивателями в верхнем полупространстве, рис. 2. Точку наблюдения M ₁ рассеянного поля зададим радиус-вектором r ₁ , а положение элементарного участка рассеивающей поверхности определим радиус-вектором р = р ( x ' , y ' ,0 ) .

Для описания потенциала,  созданного элементарным участком    dx' dy'

рассеивающей поверхности, воспользуемся соотношением:

dY = ^xy) ■ exp(-ikо r - ~PJ • n(x', y') I ri - p dx' dy';

Ф( x ', y ’) = Vs-Ч^x', y ',0), где n(x', y')- концентрация рассеивателей в плоскости z = 0; VS - коэффициент рассеяния одиночного рассеивателя. Функция двух переменных n (x', y') в настоящей работе не конкретизируется и считается заданной. Тогда выражение (8) можно представить в виде:

d Y =

V S

• exp

( x ) 2 cos ² 0 + ( y ) ²                     _ ^K

----------⁺ ik 0 ^x ■ sin ⁰ 0 - ik 0 r i - p\ )

R ₀

■ n ( x ' , y ' ) dx'dy' .

I r i

^^^^a

p

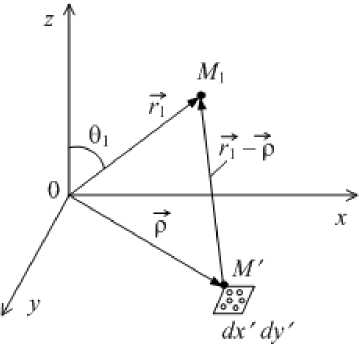
Рис. 2.

К расчету рассеянного поля

С учетом (9) рассеянное неоднородностями поле в точке наблюдения M ₁ определяем интегрированием по плоскости x'Oy' :

ж

Y = V S П

-ж

n ( x ' , y ' ) I r i - p

■ exp

( x ' ) ² cos ² 0 0 + ( y ' ) ² R 0²

+ ik ₀ x '■ sin 0 ₀ - ik ₀ Г

- p\ )

dx' dy' .

Необходимо отметить, что допустимость использования интегральных соотношений типа (10) нуждается в обосновании. Запись (10) предполагает независимость поля каждого отдельного рассеивателя от окружающих его рассеивающих неоднородностей.

Выражение (10) имеет место, когда взаимодействием рассеивателей можно пренебречь. Определим условия, при которых выполнимо данное предположение. С этой целью воспользуемся методом самосогласованного поля [4]. Представим рассеянное поле y в виде суперпозиции поля плоской падающей волны и полей, обусловленных каждым из N рассеивателей, расположенных на рассеивающей поверхности с учетом их взаимодействия:

e^Xp⁽ - ^ik 0 ^ - r ^ К - r|

N

—>

y ⁽ r i ) = ^exp^{( -} ik l ) + ^ A n ■

n =1

где коэффициенты   An ,  учитывающие взаимное влияние рассеивающих неоднородностей, подлежат определению. Если в выражении (11) перенести в левую часть слагаемое, соответствующее k-му рассеивателю, то получим поле, создаваемое всеми остальными рассеивателями совместно с падающей волной в точке наблюдения M 1 :

^ ⁽ r ) - A k •

^exp⁽ - ^ik 0 I r - r k I)

IК - Гк|

_К N

= exp(-ikr) + ^ A • n =1 n ^ k

exp^{( -} ik 0 r ^- r n I) | К — r_n\

Переместим точку наблюдения M ₁ в точку расположения k -го рассеивателя, устремив в выражении (12) величину r к значению r k . Тогда в правой части (12) получим поле, создаваемое всеми рассеивателями и плоской волной в точке, где расположен рассеиватель с номером k , исключая сам k -й рассеиватель.

Если теперь выражение для поля, создаваемого всеми рассеивателями кроме k -го, в точке, где расположен k -й рассеиватель, умножить на коэффициент рассеяния V s , то получим амплитуду поля рассеянного k -м рассеивателем:

„      ( Л exP ( - ik 0 r k

Vs exp(-ikrk) + ^An----v к к.

^V ' n =1 rk ^- rn| n * k

= A k ; k = 1... N .

Соотношения (13) представляют собой систему уравнений для определения коэффициентов A_n . Введем обозначение:

^exP ( ^{- ik} 0 r k ^{- r}n I) I r k - r l

= g ( r k , r n ) = g kn ,

g kn

g nk ,

тогда систему для определения коэффициентов рассеяния можно записать в виде:

-

A k - E V s A n g kn = V s exp ( ^- ikr k ) ; ^k = ¹... N .

n = 1 n ^ k

Выражение (14) представляет собой систему линейных алгебраических уравнений: B∙A=H с симметричной матрицей коэффициентов:

■ 1 -Vsg 12 -Vsg 13   . . -Vsg 1N B = -Vsg 21 ... 1 -Vsg 23   . .. . -Vsg 2 N . _-VsgN 1 -VsgN 2 -VsgN 3 . .1 и столбцом правых частей:

V s • ^exP⁽ - ik ’ ^r)

H =

V S • exp( - ik ■ r₂ )

...

V s ■ ^exP^{( - ik} ■ ^rN )

Рассмотрим два очевидных предельных случая – больших и малых расстояний между отдельными рассеивающими включениями. В пределе больших расстояний между неоднородностями r n - r | ^те все недиагональные компоненты матрицы B при фиксированных V S стремятся к нулевым значениям и B ^ E , где Е - единичная матрица, а для матрицы H имеет место предельное выражение:

V_s ■ exp( - ik ■ r )

H ^ H 1 =

V S ■ exp( - ik ■ r₂ )

^Vs ■ ^exP^{( - ik} ■ r N )

Поэтому выражения для всех коэффициентов A_k примут вид: ^

A k = ^Vs ■ ^exP^{( - ik} ■ r k ).                                                                           ⁽¹⁵⁾

Наличие фазового множителя в (15) связано с тем фактом, что центр рассеивающего элемента поверхности находится не в начале координат.

Приведенные рассуждения указывают на возможность применения интегрального выражения (10) для вычисления рассеянного поля, когда поверхностная плотность рассеивателей достаточно мала.

При рассмотрении второго предельного случая, когда расстояния между рассеивателями малы и можно положить \r_n -r_k\ ^ 0, необходимо одновременно учитывать асимптотическое поведение зависимости V s ( r ₀ ) при малых значениях r ₀, где r ₀ – физический размер неоднородности. В частности, если при этом выполняется условие:

.r n ^ 0| V s ⁽ r o ) g ⁽ r , r k ) = 0,                                                          (16)

I ^r 0 ^{> 0}

то матрица коэффициентов B также стремится к единичной матрице ( B ^ E ), для H имеет место предельное выражение:

V_s ■ exp( - ik ■ r )

H ^ H 2

V S ■ exp( - ik ■ r )

V S ■ exp( - ik ■ r )

и все искомые A _k примут вид: A _k = V S ■ exp( - ik ■ r ) .

Из выражения (16) следует, что для отражателей, рассеивающая способность которых с уменьшением радиуса ослабевает не медленнее чем г ₀ ^{(1 +а )} , где а >  0, суммарное поле можно представить суперпозицией полей отдельных отражателей, когда каждый из них рассеивает независимо от остальных. В случае, если указанные условия не выполняются, что может иметь место, например, для резонансных рассеивателей, интегральное выражение (10) некорректно, и необходимо учитывать взаимодействие рассеивателей.

Учитывая полученные ограничения на применение (10), выполним анализ характеристик рассеяния в дальнем поле рассеивающей области. Запишем модуль разности радиус-векторов в декартовых координатах:

| К- /51 = 7 ( ^x - x ' ) 2 ⁺( У - У ' ) 2 ^{+ z 2} , ⁽¹⁷⁾

тогда выражение (10) примет вид:

n ( x ' , y ' ) • exp

+w

^ -и-------

-от

( x ' ² cos² 0 0 + y ' ² )

------------------ - ik_ox' sin 0 - ik₀

R 2 ₀

( x - x ' ) ² + ( y - y ' ) ² + z ²

x - x ' ) ² + ( y - y ' ) ² + z ² --------------------------— dx ’ dy ' .

Обозначим характерный размер области, озвучиваемой на рассеивающей поверхности падающим пучком, через / max . Тогда для всех точек дальнего поля r 1 >>  / max будут выполнены неравенства [5, 6]:

(xx'+ yy') = (r1, /)   /• r1

<< 1 ,

2           2   <2 < r12r12r12r1

и асимптотическая формула:

7(x - x')2 +(y - y ')2 + z2 - Xx—2XX‘+T(x2УT2—2УУyj+T^-

= r 1

2       2       2

x ² + y ² + z ² r 1²

-

2 xx ' + 2 yy ' ( x ' ) ² + ( y ' ) ² Г 2

r 1²

= r 1

_ 2 xx ' + 2 yy ' P 2

¹            2        ⁺ 2

r 1²            r 1²

Г f 1 -k

x.

^r1      —

,

с учетом, которой потенциал рассеянной волны в дальней области поля равен:

+от            ^exp

V- V s ■[[ n ⁽ x ' , y ' )

-от

( x ' ) ² cos ² 0 0 + ( y ' ) ²

R 0²

- ik ₀ x ' sin 0 ₀ - ik ₀ r 1 1

k

xx ' + yy '^

г2

^r1     —

- dx' dy ' .

Г 1

k

^r 1      —

Пренебрегая членом ( xx ' + yy ' )/ r² в амплитудном множителе подынтегрального выражения, после очевидных упрощений получаем:

exp ^(— kr ) 7f p

Ж = VS •

--J Пп(x,y )x r1

X exp

⁽ x ) cos O_o +⁽ y )        , . xx + yy

- —---- 20---——i^k о ^x sin ⁰ о ⁺ i ^k о---2--

R 0²                                       r 1²

dx 'dy' .

Выражение (19) дает значения потенциала в дальней области поля, созданного рассеивающей поверхностью, где для каждой точки выполняется условие р maj r <<  1.

Для удобства анализа рассеянного поля в выражении (19) перейдем к сферической системе координат:

Щ ⁽ r, ф ,в ) = V •

exp ( - ik ₀ r )

r ₁

к 2 п

• J J ^{п (} р, ф ' ) • ^exp <

р ² cos ² ф' • cos ² 0 ₀ + р ² sin ² ф '

R

+

+ ik ₀ р [ cos ф' • sin в ₀ + sin 0 • cos ( ф - ф ' ) ] } • р dpd ф' .

Рассмотрим потенциал рассеянного поля в плоскости падения звукового пучка (плоскости, проходящей через ось пучка и координатную ось Oz ). Плоскость падения определяется двумя значениями угла ф : ф = 0 и ф = п . В результате выражение (20) принимает вид:

Щ ⁽ Г, ф ,в ) = Vs •

exp ( - ik ₀ r )

r ₁

к 2 п

• J J ^{п (} р, фТ exp *

р ² cos ² ф' • cos ² в ₀ + р ² sin ² ф '

R

+

+ ik ₀ р cos ф ' • ( sin в ₀ ± sin в )} • р dрd ф ' ,

где знаки «+» и «-» в фазовом множителе соответствуют случаям ф = 0 и ф = п .

В соотношении (21) множитель V_S является комплексной величиной и содержит фазу коэффициента рассеяния, величина exp ( — ik ₀ r 1 )/ r 1 представляет собой пространственный набег фазы, экспонента в подынтегральном выражении описывает третье фазовое слагаемое – интерференционная фазовая добавка. При проектировании системы распознавания на основе акустической жесткости рассеивателей, в анализе формально нуждаются три перечисленные характеристики рассеянного сигнала. Несмотря на это, два из трех указанных факторов в данной задаче не представляют интереса. Пространственный набег фазы не будет нести полезной информации, поскольку представляет собой шум, поэтому необходимо его подавление. Меры борьбы с пространственным набегом фазы изложены в монографиях [7, 8]. Интерференционная фаза может быть скорректирована за счет изменения расстояния между источником сигнала и исследуемой областью.

ЗАКЛЮЧЕНИЕ

Полученное выражение (21) для потенциала рассеянной волны позволяет выполнить анализ влияния пространственного распределения концентрации рассеивателей, геометрии озвученной области, из которой происходит рассеяние, характеристик единичного рассеивателя на амплитудные и фазовые характеристики рассеянного сигнала.

Из выражения (21) видно, что единственным фазовым множителем является величина:

exp [ ik₀ p cos p' ■( sin 0 0 ± sin 0 ) ] .

Фаза в показателе экспоненты обращается в нуль, если:

• 1) . - при любом из двух значений азимутальных углов ( ф = 0 или ф = п ) имеем 0 = 0 (обратное рассеяние по нормали к рассеивающей поверхности);

• 2) . - при ф = п имеем 0 = 0 0 (направление зеркального отражения).

При выполнении указанных условий фаза рассеянной в соответствующих направлениях волн не испытывает дополнительного фазового сдвига при любых возможных значениях вышеперечисленных факторов (концентрации рассеивателей, геометрии озвученной области), а зависит только от свойств рассеивателя (фазы коэффициента рассеяния).

В то же время амплитудное значение рассеянного поля является функцией указанных факторов при любых углах рассеяния.

В качестве направления дальнейшей работы можно отметить, что полученные результаты могут быть использованы для анализа рассеянных полей, полученных на слое, содержащем неоднородности нескольких видов. Интегралы, подобные (21), могут быть в той или иной форме записаны для каждого вида неоднородностей и с целью получения картины результирующего поля просуммированы, поскольку используемый нами метод самосогласованного поля указывает на аддитивный характер поля, полученного в результате озвучивания области, содержащей различные неоднородности. Важным также является вопрос оценки погрешностей, возникающих при замене матрицы коэффициентов B на единичную матрицу в обоих случаях предельного расстояния между рассеивателями. Однако эти вопросы выходят за пределы настоящей работы и будут рассмотрены в дальнейшем.