Рассеяние радиоимпульсов на идеально проводящей разомкнутой цилиндрической поверхности

Разомкнутые цилиндрические поверхности являются элементами конструкций волноводных антенн, резонаторов [1] и искусственных метаматериалов с анизотропными электрофизическими параметрами [2–4]. Исследование их рассеивающих свойств имеет важное практическое значение для оценки электромагнитной совместимости приемопередающих устройств диапазона сверхвысоких частот [1] и создания кираль-ных покрытий [2; 4] в интересах снижения радиолокационной заметности объектов.

В [3; 4] методом сингулярных интегральных уравнений (ИУ) решена задача дифракции плоской монохроматической электромагнитной волны на идеально проводящей бесконечно тонкой цилиндрической поверхности с продольным разрывом.

В предлагаемой работе на основе численного решения ИУ Фредгольма первого рода с пространственно-временными дифференциальными операторами второго порядка [5] исследовано вторичное излучение указанным объектом радиоимпульсов с прямоугольной и гауссовской огибающими, применяемых в широкополосных и сверхширокополосных радиосистемах [6].

Цель работы – анализ зависимостей энергетической диаграммы обратного рассеяния (ДОР) [6; 7] поверхности от ее электрических размеров, вида и параметров возбуждающих сигналов.

Для нахождения поверхностных токов рассеивателя введем цилиндрическую систему координат

( ρ, ϕ, z ) , для расчета вторичного электрического поля и энергетической ДОР – сферическую систему координат ( r , θ, ϕ ) . Центры выбранных систем координат совмещены; угол θ отсчитывается от оси Oz .

Обозначим радиус цилиндра a , высоту – h , угловую ширину разрыва поверхности – ∆, подразумевая, что h <<2π a , ∆ << 2π; центральная продольная линия рассеивателя совпадает с осью Oz , торцевые кромки находятся в плоскостях z = ± h 2, а разрыв – в области ϕ < ∆ 2.

Плотность поверхностных токов рассеивателя в момент времени t содержит азимутальную j ϕ ( ϕ, z , t ) и продольную j_z ( ϕ, z , t ) составляющие ( z ≤ h 2; ϕ ≥ ∆ 2); его вторичное электрическое поле в дальней зоне [5; 6] – меридиональный E q ( r , 9, ф, t ) и азимутальный E ф ( r , 9, ф, t ) поляризационные компоненты.

Энергетическая ДОР объекта определяется выражением [6]

D ( θ,ϕ ) =    χ ( θ^,ϕ ) ,                            (1)

max χ ( θ, ϕ ) θ , ϕ где ∞

X ( 9, ф ) = J X t ( 9, Ф, t ) dt                           (2)

-∞

– угловая зависимость плотности потока энергии отраженного поля [7; 8];

X t ( 9, Ф, t ) = 4^ lim r ² I E ( r , 9, ф, t )               (3)

W ₀ r →∞

– угло-временное распределение плотности потока рассеиваемой в пространстве энергии [8];

|E ( r , 6, ф> t ) = V E 2 ( r , 6, Ф, t ) + E 2 ( r , 6, Ф, t )

– текущее значение амплитуды рассеянного поля в пространственно-временной области; W ₀ – волновое сопротивление свободного пространства. Выражения для расчета E о [ ф ] ( r , 6, ф, t ) по распределению j z [ ф ] ( ф, z , t ) на объекте приведены в [5].

При нахождении токов исследуемой разомкнутой цилиндрической поверхности будем полагать, ^что j z [ ф ] ( ±^л/ 2, ^z , t ) =0, j z [ ф ] ( ф, ± hl 2, t ) =0;^то-ками, затекающими за кромку, ввиду бесконечно малой толщины поверхности можно пренебречь. Фронт облучающей волны является плоским; вектор электрического поля ортогонален плоскости, проходящей через вектор, характеризующий направление на источник сигнала, и ось Oz . Тангенциальная составляющая поля прямоугольного радиоимпульса на поверхности с границами р = a , |ф| > Л/2, | z | =< h /2 имеет вид

E ig ( Z , 6, ф , t ) =

'Е q sin ^6x

Г f a cos 6 cos ф + z sin ф) )

x cos tog t--+ Фо

ll          C J J (4)

при - ^T <  t <  ^T , 2       2

т т 0 при t < —, t > —, I                 2       2

где E q , ® q , Фо и т — амплитуда, циклическая частота несущей, начальная фаза и длительность импульса; c – скорость света; текущее значение осевой проекции напряженности поля радиоимпульса с гауссовской огибающей определяется

Az (z, ф, t ) =

Цо a 4n

2 п-Л/ 2

J

Л/ 2

h 2

J j

- h / 2

z ', ф', t

xЛR 1 (z - z',ф)dz'dф',

где

ЛR (z - z', ф ) = (z - z')2 + 4a2 sin2 I ф

выражением

E ig ( z , 6, ф, t ) = E o sin 6x

x exp

', I t 12т² l

-

a cos 6 cos ф + z sin 6 )

-----------------------------------------------------------------------------------------------------------------------------I

c J

x

x cos I too I t -

J a cos 6 cos ф + z sin 6 )      )

I ^{+ ф} 0 I.

c J J

Учитывая обрыв распределения токов на краях

поверхности, компоненты ее векторного потенциала в области р = a , |ф| > Л/2, | z | =< h /2 определим следующим образом [5]

Aф(z, ф, t ) =

Цо a 4п

2 п-Л/ 2

I

Л/ 2

h 2

J j ф I z ', ф‘, t - - h 2    ^l

ЛR (z - z', ф)) ---------------------  I x

с J

x

cos ф

Л R ( z - z ', ф )

dz' d ф',

Л R (z - с

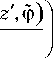
x

ф = ф - ф', Цо — магнитная проницаемость вакуума.

Из условий непрерывности тангенциальной составляющей электрического поля на идеально проводящей поверхности получим систему уравнений для (4), (5) как проекции векторного волнового уравнения [5] на оси цилиндрической системы координат:

д2

д z ²

-

д 2

^е 0 ^Ц о a t ¹ A z ^{( z} , ^ф , t ⁾⁺

+1 d² A ф ( z , ф, t )

<

a    dz дф

1 д2 Az (z, ф, t) a д z дф

-

д

' = -eo ^IEtg (z,6, ф,t)’ д t д2 Aф(z, ф, t) eo Цо     П +

д t2

1 д² A ф ( z , ф, t )

⁺ a ²     дф²

Iф|>Л/2, | z | <  h 2,

где Eq — диэлектрическая проницаемость вакуума.

Согласно [9], для максимизации плотности потока энергии вторичного излучения [8] длительность возбуждающего импульса необходимо выбирать таким образом, чтобы за время т он распространялся на достаточно малой части поверхности. В этом случае, с учетом введенного ранее условия о малости ширины цилиндрической поверхности относительно длины, время запаздывания сигнала при распространении в направлении оси Oz полагается несущественным.

Разложим компоненты векторного потенциала (6) и плотности поверхностного тока рассеивателя в комплексные ряды Фурье по координате ф да

Az[ф](z, ф, t)= Е Пz[ф]n (z, t)exp (jnф) , (8) n=-да да jz [ф]( z, ф, t)= Е jz [ф] n (z, t )exp (jn ф),    (9)

n=-да где П z [ф] n (z, t ) и jz [ф] n (z, t ) - пространственновременное распределение азимутальных гармо-

ник A z [ ф ] ( z , ф, t ) и j z [ ф ] ( z , ф, t ) соответственно. В результате подстановки (8) и (9) в (6) и приравнивания коэффициентов при комплексных экспонентах с одинаковыми показателями на-

p Г Г z sin 9)

2 (—1) cos I №0 I t--I + V0 Ik c J

ходим

n z [ф] n (z, t ) = h2

= ^ 0 a j j z [ ф ] n ⁽ z', t S n ⁽ z ’ z ' ) dz '’

— h /2

где

при n = 2 p + 1,

x1

~ P . 1 L z sin9)

^£ n ( ^— 1 ) ^sin| ^№ 0 I t --I ⁺ Ф 0 ^{k k} c ^J

_при n = 2 p , p = 0,1, 2 ^ ,

2 п—А/ 2

S z I     exp ( ,n ^ф ) d ф.

n ( , )    Aj 2 А R (z — z 'ф)

Аппроксимируем тангенциальные

проекции

электрического поля (4) и (5) рядами Фурье – Бесселя [10] по азимутальным гармоникам, подставим полученные выражения в правую часть (7) и с учетом (6), (8), (10), (11) получим систему ИУ Фредгольма первого рода с пространственно-временными дифференциальными операторами второго порядка относительно азимутальных гармоник j z [ ф ] n ( z , t ) плотности поверхностных токов объекта j z [ ф ] ( z , ф, t ) :

' h /2 г

—

j

h /2 ^L

d ² dz ²

—

d ²    .

^s0 ^ 0-y j zn ^{( z}, t ) dt ²

х

<

h 2

^х S n ( ^z , ^z ' ) ^dz ' + jn^ I" j ф n ( ^z '> t ) ^x a dz

— h /2

x Sn (z, z')dz'=£0E0Fn (z, t), h2

j1" f jzn (z', t)Sn (z ’ z')dz' + a dz

— h /2

+

х

2 n )

—

a

h 2

—

d ²

^s 0 ^ 0 """Г dt ²

х

j ^j ф n ( ^z ', t ) S n ( ^z , ^z ' ) dz ' = 0, h 2

I z I <  h 2, n = 0, 1, 2...,

где

F_n 1 ( z , t ) для сигнала ( 4 ) ,

Fn (z, t) =

Г 1 Г exp--, I t

I 2 t2 I

—

z

— cos 9

c

х

^x ( F n 1 ( ^z , t ) ⁺ F n 2 ( ^z , t ) )

для сигнала ( 5 ) ,

F_n 1 = 4 л ® 0 J_n I ^Ю0 a sin 9 I x

I c J

Г too a      ) Г t — z sin 9/c )

Fn2 = 4л Jn I----sin 9 I x I-------—f— I x

k c JI t2 J

„.- p Г Г z sin 9)      )

2 (—1) cos l№01 t      c— I + V0 I

при n = 2p + 1, x<

s n (—1) p sin | №0 | t

_при

^         1

s=

n |2

—

z sin 9)

-------I + Ф0

k k c n = 2p, p = 0,1, 2^,

при n = 0, при n >0

— символ Неймана, J_n ( _ ) — функция Бесселя первого рода n -го порядка.

Из (12) следует, что распределение нулевой

гармоники плотности поверхностного тока удов-

летворяет уравнению

h 2 j — h /2

d ² dz ²

d ²

^{— s} 0 ^0 """"Л" dt ²

j z 0 ( ^z ', t ) ^x

x S 0 ( z , z ') dz' = S 0 E 0 F ( z , t ) .

При A^ 0 функция S 0 ( z , z ' ) , согласно (11), приобретает смысл весового коэффициента нулевой пространственной гармоники ряда Фурье для функции точечного источника на цилиндрической поверхности [5], а (12) и (16) преобразуются в задачу симметричного возбуждения цилиндра. При a ^ 0, вследствие малых азимутальных вариаций поверхностных токов j z [ ф ] ( z , ф, t ) , можно полагать, что j ф ( z , ф, t ) « 0, а j z ( z , ф, t ) * j z 0 ( z , t ) . В результате замены j _z 0 ( z , t ) эквивалентным током I_z ( z , t ) = 2л aj z 0 ( z , t ) нитевидного источника, расположенного на оси Oz , ИУ (16) преобразуется в задачу для импульсного возбуждения трубчатого цилиндра [11].

Решение системы (12) ввиду математической некорректности входящих в нее уравнений [10] будем осуществлять численно при аппроксимации пространственно-временного распределения гармоник плотности токов произведением пространственной и временной последовательностей кусочно-постоянных функций.

Рис. 1

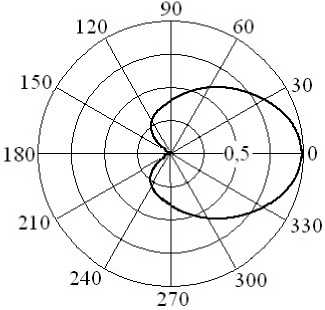
Рис. 2

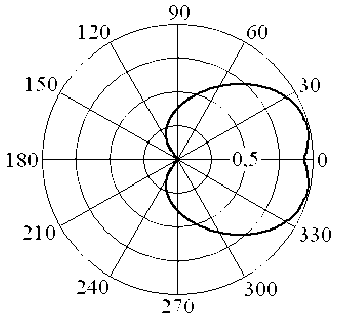
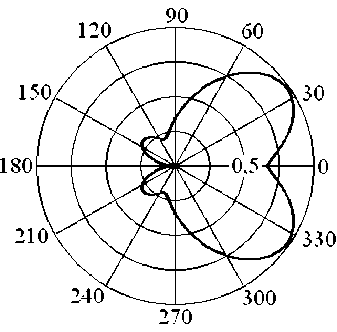
Рис. 3

Вследствие представления jz [ф]n (z, t) множеством весовых коэффициентов аппроксимирующих последовательностей на интервалах дискретизации ширины кольца Az и длительности импульса At, удовлетворяющих условию Az = c At, система ИУ (12) преобразуется в систему линейных алгебраических уравнений (СЛАУ) с матричным оператором Фредгольма [10] относительно множества значений гармоник токов в фиксированных точках пространственно-временной области. Для стабилизации разностных схем вычисления производных [11] в (12), обеспечения монотонной сходимости и устойчивости решения полученной СЛАУ коэффициенты аппроксимации jzn(z, t) и jФn(z, t), как показано в [11; 12], требуется вычислять в точках, смещенных по Oz и оси вре- мени на половину интервалов дискретизации.

На основе численного решения СЛАУ, обеспе- чивающего частичное обращение оператора за- дачи импульсного возбуждения цилиндрической расчета j [ф]n(z, t),

поверхности при точности

обратно пропорциональной длинам аппроксими- рующих последовательностей в четвертой степени [10], с использованием (9) вычислены компоненты плотности токов разомкнутой цилиндрической поверхности, возбуждаемой радиоим-

Рис. 4

пульсами (4) и (5). Путем подстановки найденного в соответствии с [5] вторичного поля объекта в (3), а полученных результатов – последовательно в (2) и (1) проведен расчет его энергетической ДОР.

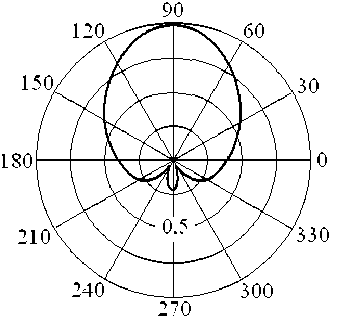
На рис. 1 и 2 соответственно приведены энергетические ДОР цилиндрической поверхности D ф ( ф ) = D ( п/2, ф ) с шириной разрыва A = п /15 и нормированным радиусом поперечного сечения a/h = 5,3, облучаемой прямоугольным и гауссовским радиоимпульсами длительностью т = 5 h/c с циклической частотой несущей to o = 5п/т. На рис. 3 представлена зависимость D ф ( ф ) , а на рис. 4 — зависимость D q ( 9 ) = D ( 9, 0 ) , характеризующие угловое распределение плотности энергии вторичного поля поверхности с соотношением размеров a/h = 5,8 при возбуждении радиоимпульсом с гауссовской огибающей.

Согласно полученным результатам, вторичное излучение радиоимпульсов в азимутальной плоскости (рис. 1–3) носит анизотропный характер, выявленный в [3] при анализе рассеяния монохроматических электромагнитных волн. Энергетическая ДОР цилиндрической поверхности, возбуждаемой прямоугольным радиоимпульсом, содержит максимум в направлении ее разрыва.

При рассеянии радиоимпульса с гауссовской огибающей, эквивалентная длительность [8] которого превышает длительность прямоугольного радиоимпульса в 1,2…1,35 раз, происходит расширение ДОР, обусловленное уменьшением электрических размеров объекта [8]. При увеличении a h с 5,3 до 5,8 наблюдается дополнительное снижение плотности потока энергии поля, рассеянного в направлении ϕ = 0, в 1,4 раз.

По мере увеличения длительности радиоимпульсов энергетическая ДОР цилиндрической поверхности в меридиональной плоскости приобретает форму, представленную в [4] по результатам решения задачи рассеяния гармонического поля. При возрастании τ в 5…7,5 раз уровень заднего бокового лепестка ДОР, приведенной на рис. 4, убывает на 2,2…2,8 дБ.

С увеличением циклической частоты несущей с ω₀ = 5π τ до ω₀ = 9π τ при неизменной длительности возбуждающего импульса ширина энергетической ДОР исследуемой поверхности при a h = 2,8…5,3 уменьшается не менее чем в 1,2 раза.

Таким образом, на основе численного решения системы ИУ Фредгольма первого рода относительно пространственно-временного распределения азимутальных гармоник токов проведен анализ вторичного излучения радиоимпульсов идеально проводящей разомкнутой цилиндрической поверхностью. Исследованы закономерности изменения ее энергетической ДОР в зависимости от электрических размеров, вида и параметров облучающих сигналов.