Рассеяние радиоимпульсов на разомкнутом идеально проводящем кольце

Исследование рассеяния радиоимпульсов на разомкнутом идеально проводящем кольце имеет практически важное значение для оценки радиолокационной заметности рамочных антенн [1; 2] и создания искусственных метаструктур с анизотропными отражательными свойствами [3].

В [2] с использованием интегральных уравнений Фредгольма первого рода [4] с экспоненциальной функцией Грина [1; 2] в приближении эквивалентного тока осевого нитевидного источника [2; 5] построена модель гармонического возбуждения и проведен анализ диаграммы рассеяния (ДР) круглой рамки из проводника с малым электрическим радиусом поперечного сечения. В [3; 6] методом сингулярных интегральных уравнений решена самосогласованная задача дифракции [1] плоской монохроматической электромагнитной волны на цилиндрическом, а в [7] – на плоском кольце из бесконечно тонкой узкой полоски с поперечным разрывом.

В предлагаемой работе на основе частичного обращения операторов [4; 8] пространственновременных интегро-дифференциальных уравнений (ИДУ) относительно эквивалентного осевого распределения тока и заряда [5] выявлены закономерности вторичного излучения радиоимпульсов с прямоугольной и гауссовской огибающими разомкнутым кольцом из трубки малого электрического радиуса [5; 8] поперечного сечения с бесконечно тонкими идеально проводящими стенками.

Цель работы – анализ зависимостей энергетической ДР объекта [9] от его электрических размеров, вида и параметров облучающих сигналов.

Будем полагать, что кольцо расположено в плоскости z = 0 цилиндрической системы координат ( р, ф, z ) , ось Oz проходит через его центр, края разрыва поверхности равноудалены от направления ф = 0. Радиус кольца, измеряемый как расстояние от точки О до центральной продольной оси трубки, обозначим R ₀, радиус трубки — а о , угловую ширину разрыва — 2А, подразумевая, что а о <<  R o , А < 2п.

Пространственный фронт облучающего радио- импульса является плоским; вектор электрического поля лежит в плоскости, проходящей через вектор, характеризующий направление на источник сигнала фо, и ось, ортогональную Oz.

При длительности радиоимпульса т >> а о /с, где c – скорость света, поверхностному току кольца в каждый момент времени t сопоставим эквивалентный ток I (ф, t) нитевидного источника, удовлетворяющий граничным условиям I (±А, t) = 0; поверхностный заряд представим распределением его удельной плотности q(ф, t) на окружности радиуса R0 в секторе углов ф е [-А; А]. Амплитуды реальных и эквивалентных токов и зарядов, как показано в [8], отличаются на малую величину порядка O (а0 ); смещением их зависимостей от времени Ат = а0 /с можно пренебречь, поскольку Ат << т.

Энергетическая ДР объекта определяется выражением [9]

х ( ф ; фо )

D ( ф ; фо ) =           ^—_х,                      ⁽¹⁾

max X (ф; Фо )

Ф где

ю

х ( ф ; фо ) = J x t ( ф , t ; фо ) dt                       (2)

-ю

– угловая зависимость плотности потока энергии отраженного поля;

X t ( ф, t ; Фо ) =      lim r ² E ( r , Ф, t ; Фо ) 2           (3)

M g r ^ю

ского поля, условие непрерывности его тан-

генциальной проекции на поверхности кольца

c учетом калибровки Лоренца [10], запишем

систему пространственно-временных ИДУ для

I ( ф , t ) и q ( ф , t ) :

Цо д

4n dt

l

A I

I-

-A

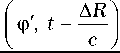
– угло-временное распределение плотности потока рассеиваемой в пространстве энергии; |E ( r , ф, t ; Фо )| — текущее значение амплитуды рассеянного поля в пространственно-временной области; W ₀ – волновое сопротивление свободного пространства; r – расстояние от начала системы координат до точки наблюдения.

Для исследуемого кольца с разрывом зависимость | E ( r , ф, t ; ф о )| в (3) находится как сумма квадратов текущих значений азимутальной и радиальной составляющих рассеянного поля; выражения для расчета поляризационных компонентов поля по распределению токов объекта приведены в [10].

Касательная составляющая облучающего прямоугольного радиоимпульса на поверхности рассеивателя имеет вид

Etg (ф, t; Фо ) =

| Г   Ro cos (ф-ф0))

Ео cos I too I t--I + Фо

c

= < при--< t < —, 2       2

n             т т

0 при t < - , t > , 22

где E o , to o и V o — амплитуда, циклическая частота несущей и начальная фаза импульса; текущее значение тангенциальной проекции напряженности поля радиоимпульса с гауссовской огибающей определяется выражением

^E ig ( ф, t ; Ф 0 ) =

= E o exp

1 (

—2 I t 2т² (

-

Ro cos (Ф — Фо) |

c J

x

xcos too

Ro cos (ф - Фо) t-- c

)

+ Ф0

J

Используя определение векторного и скалярного потенциалов, напряженности электриче-

1 d

+---

4 лбо дф

A q I ф', t -

^c-^ dФ' =

AR

-A

” = ^E tg ( ф, t ; Ф о ) ,

1 д

Ro дф

д

+ — д t

где

A 11 ф', t -^

AR

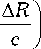
d ф' +

-A

A q | ф', t -^

AR

d ф' = 0,

-A

AR = Ro

4 sin2

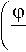
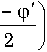
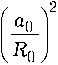
– расстояние между точкой интегрирования на осевой линии распределения эквивалентных токов и зарядов и точкой наблюдения на поверхности кольца; S o и Цо — диэлектрическая и магнитная проницаемость вакуума.

Для численного решения системы ИДУ (6)

применим кусочно-постоянную аппроксимацию зависимостей I ( ф, t ) и q ( ф, t ) произведением последовательностей из N функций в секторах углов Aф и M функций на интервалах времени A t ; частные производные указанных функций по Ф и t вычисляются с применением разностных схем [5; 8; 11].

В результате представления эквивалентно-

го тока кольца дискретными значениями a nm , n = 1 ^ N , m = 1 ^ M , а удельной плотности заряда — множеством отсчетов в _nm , n = 1 ^ N , m = 1 ^ M система ИДУ (6) преобразуется в систему линейных алгебраических уравнений (СЛАУ) с матричным оператором фредгольмово-го типа [4] размером N x N для каждого из M

моментов времени anmF (0) + Xn,m + Ynim = Ynm, n = 1_ N, m = 1_ M,

где

N

Xnm =   ^   ak,m-|m-к|Л (n - k) - к=1, m-| n - к| >0

N

-    £    “к,m-1-| n-k Л( n - k ), k =1, m-1-| n - к| >0

N - 1

Ynm =     ^ вк, m-1-|n+1-к| Q(|n + 1 - к|)- к =1, m-1-| n+1-к| >0

N - 1

^- Z    ^в к , m - 1 -1 n - к | ^Q( n ^- k ) ;

к =1, m-1-| n - к| >0

у _nm = E tg ( n Аф, m A t ; ф 0 ) — элементы вектор-столбца N удельных эквивалентных потенциалов, определяемые значениями комплексной амплитуды возбуждающего поля на поверхности кольца в направлении ф = ( n - 1 ) Аф, n = 1... N , в момент времени t = ( m - 1 ) A t , m = 1... M ;

Л ( n - к |)=^ ^ F(h_Z^k |), n , к = 1_ n (10) 4n A t

–

элементы матрицы

погонных импедансов

кольца;

/-V

Q (|n - к|) =

F (ln - к)

4п Б0 R0 Аф ’

n, к = 1... N

–

элементы матрицы

обращенных

емкостей

кольца;

F ^{( к - n} l ) =

,                    =• x

V a 0 ^{+ 4} R 0

x

F

arcsin

^:2 sin ^ф +-n|

V

a 0 + ^{4 R} 2 sin^{2 ф} |+_ n

,

2^_

0 + 4 R 0 ))

-

-F

arcsin

V a ^{2 + 4} R 0 sin ^ф|

I к - n|

,

V

a ² + 4 R 2 sin^{2 ф}| _{к -} n

2 R_L= 0 + 4 R 0 ))_

;

ф |±- n = (| к - n | ± 0,5 ) Аф, F ( k , p ) — эллиптический интеграл первого рода [11].

Решение СЛАУ (7) выполнено методом Гаусса с выбором главного элемента по столб-

Рис. 1

цу [11] при последовательном продвижении по времени. Интервал A t определялся по теореме Котельникова [12] для верхней границы эквивалентной полосы циклических частот возбуждающего сигнала [9; 13], величина Аф = с A t/R 0 . Согласно [8], при выбранных значениях A t и Аф обеспечиваются стабилизация разностных схем вычисления производных, устойчивость частичного обращения матричного оператора [4] и монотонная сходимость последовательностей, аппроксимирующих I ( ф, t ) и q ( ф, t ) . С учетом обращения эквивалентного тока в нуль при ф = ±А коэффициенты a _nm , n = 1 ^ N , m = 1 ^ M рассчитывались в центральных точках интервалов Аф, а значения в _nm , n = 1 ^ N , m = 1 ^ M — в точках, смещенных на Аф/2 по азимутальной координате и на A t /2 оси времени.

По найденному распределению эквивалентного тока и удельной плотности заряда в соответствии с [10] рассчитано вторичное поле; путем последовательной подстановки полученных результатов в (3), (2), (1) вычислена энергетическая ДР разомкнутого кольца.

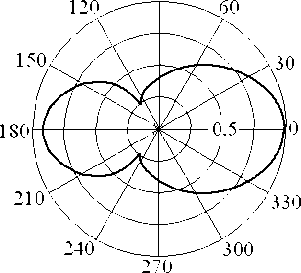
На рис. 1 приведена энергетическая ДР кольца с шириной разрыва 2А = п /15 и относительными размерами a 0 / R 0 = 0,09, облучаемого с направления ф 0 = 0 прямоугольным радиоимпульсом длительности т = 6,25 R 0 / с с циклической частотой ® 0 = 2п/т и начальной фазой Ф 0 = 0; на рис. 2 представлена энергетическая ДР кольца, возбуждаемого сигналом с гауссовской огибающей.

Из полученных результатов следует, что по аналогии с рассеянием монохроматических процессов [3; 6; 7] импульсные сигналы, переизлученные разомкнутым кольцом, имеют анизотропное угловое распределение. Энергетическая ДР кольца, возбуждаемого прямоугольным радиоимпульсом, содержит максимум в направлении, противоположном разрыву. При воздействии сигнала с гауссовской огибающей,

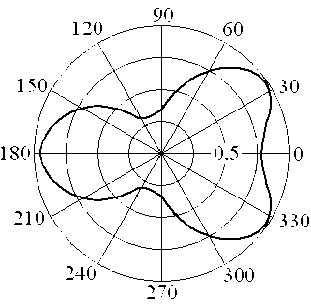
Рис. 2

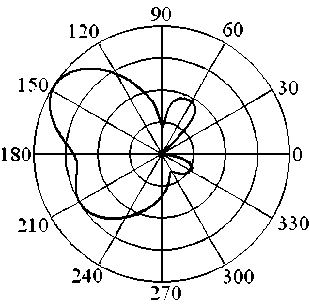
Рис. 4

эквивалентная длительность [13] которого составляет 1,2... 1,35т, в ДР появляется локальный экстремум в направлении ϕ=π, обусловленный уменьшением электрических размеров объекта по сравнению со случаем возбуждения прямоугольным радиоимпульсом.

Установлено, что при уменьшении длительности сигнала в 1,2…1,4 раз или увеличении ширины разрыва кольца в 2,5…3,2 раз плотность потока энергии поля, рассеянного в направлении на источник радиоизлучения, возрастает на 1,3…1,7 дБ. При увеличении длительности прямоугольного радиоимпульса свыше τ=7,12 R ₀ c в ДР кольца в направлении ϕ=π формируется провал, величина которого за счет изменения ширины разрыва от 2∆=π 15 до 2∆=π 5 возрастает на 1,7 дБ.

С увеличением циклической частоты несущей в 1,5…2,5 раза ширина энергетической ДР кольца уменьшается не менее чем в 1,2…1,35 раза. При возрастании τ в 5…7,5 раза уровень заднего лепестка энергетической ДР, приведенной на рис. 1, убывает на 2,2…2,5 дБ.

На рис. 3 и 4 представлены энергетические ДР кольца, облучаемого прямоугольным радиоимпульсом с направлений ϕ0 =π и ϕ0 =π2 соответственно. Электрические размеры кольца

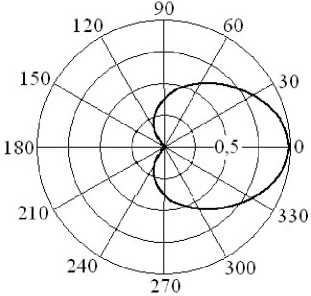
Рис. 3

и частотно-временные параметры облучающих сигналов выбраны такими же, как при расчете зависимости на рис. 1.

Из анализа рис. 3 следует, что ДР в направлении на источник радиоизлучения содержит нуль. По мере снижения длительности радиоимпульса в 1,3…1,5 раза возникает эффект «заплывания» нуля [9; 13] при снижении плотности потока энергии вторичного излучения в направлении ϕ=0 на 2,3…3,6 дБ.

За счет увеличения длительности сигнала в 2,5…3,5 раза средний уровень боковых лепестков ДР кольца возрастает на 1,2…1,4 дБ по сравнению с зависимостью, представленной на рис. 4, с появлением локальных экстремумов глубиной 4,4…4,5 дБ.

Таким образом, на основе численного решения ИДУ с пространственно-временными операторами относительно эквивалентного осевого распределения тока и заряда проведен анализ вторичного излучения радиоимпульсов разомкнутым кольцом из идеально проводящей трубки с малым электрическим радиусом поперечного сечения и бесконечно тонкими стенками. Исследовано влияние вида и параметров облучающих сигналов, а также электрических размеров кольца на его ДР.