Рассеяние радиоимпульсов на разомкнутом тонком кольце с перпендикулярными его плоскости отрезками на краях разрыва
Автор: Разиньков С.Н., Разинькова О.Э.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 2 т.18, 2015 года.
Бесплатный доступ
На основе численного решения интегро-дифференциальных уравнений с пространственно-временными операторами для эквивалентных осевых распределений токов и зарядов проведен анализ вторичного излучения радиоимпульсов зеркально-асимметричным элементом в виде разомкнутого кольца с перпендикулярными его плоскости отрезками на краях разрыва. Исследовано влияние аналитических свойств огибающих и частотно-временных параметров облучающих сигналов на энергетическую диаграмму рассеяния объекта.
Зеркально-асимметричный элемент, радиоимпульс, интегро-дифференциальное уравнение с пространственно-временным оператором, энергетическая диаграмма рассеяния объекта
Короткий адрес: https://sciup.org/140255913
IDR: 140255913
Текст научной статьи Рассеяние радиоимпульсов на разомкнутом тонком кольце с перпендикулярными его плоскости отрезками на краях разрыва
Токопроводящие зеркально-асимметричные элементы в виде разомкнутых колец с присоединенными к краям разрывов параллельными отрезками являются базовыми компонентами искусственных метаматериалов с анизотропными отражательными свойствами [1; 2]. Среда, в которую внедрены периодические структуры из указанных элементов, характеризуется отрицательным коэффициентом преломления вследствие одновременно отрицательных значений ее диэлектрической и магнитной проницаемости [2; 3].
В [1] с использованием сингулярных интегральных уравнений относительно азимутального распределения плотности поверхностного тока кольца и эквивалентных токов присоединенных отрезков в квазистатическом приближении [4] решена самосогласованная задача [4] дифракции плоской монохроматической электромагнитной волны на зеркально-асимметричных элементах. Показано, что при расположении присоединенных отрезков перпендикулярно плоскости кольца смена направления прихода облучающей волны приводит к изменению уровня вторичного излучения при практически инвариантной диаграмме рассеяния (ДР) элемента.
В предлагаемой работе на основе численного решения интегро-дифференциальных уравнений (ИДУ) с пространственно-временными операторами относительно эквивалентного осевого распределения тока и заряда [5] путем последо- вательного продвижения по времени [6] проведен расчет энергетической ДР [7] разомкнутого тонкого кольца с перпендикулярными его плоскости отрезками на краях разрыва, возбуждаемого радиоимпульсами с прямоугольной и гауссовской огибающими. Эти исследования представляют интерес для создания диапазонных метаматериалов [8] и оценки эффективности их применения для защиты объектов от средств радиолокационной разведки с широкополосными и сверхширокополосными сигналами [9; 10].
Цель работы – анализ влияния аналитических свойств огибающих и частотно-временных параметров облучающих радиоимпульсов на энергетическую ДР элемента.
Для получения ИДУ относительно токов и зарядов исследуемого объекта введем цилиндрическую систему координат ( р, ф, z ) , а для расчета его поля и энергетической ДР – сферическую систему координат ( r , ф, 9 ) , центры которых совмещены.
Будем полагать, что рассеиватель выполнен из идеально проводящего материала. Радиус кольца, определяемый как расстояние от его центра до центральной продольной оси проводника, обозначим R 0, длину каждого присоединенного отрезка l 0, радиус трубки a 0, угловую ширину разрыва 2А, подразумевая, что a о значительно меньше R 0, l 0 и пространственной длительности облучающего радиоимпульса, А < п.
Кольцо расположено в плоскости z = 0 цилиндрической системы координат, ось Oz проходит через его центр, края разрыва поверхности равноудалены от направления ф = 0. Отрезки, присоединенные к кольцу в точках с азимутальными координатами ф = ( —1 ) к А, к = 1, 2, параллельны оси Oz и занимают нижнюю (при к = 1) и верхнюю (при к = 2) относительно плоскости z = 0 части полупространства; их свободные концы принадлежат плоскостям z = ( —1 ) к I 0 , к = 1, 2.
Пространственный фронт облучающего радиоимпульса является плоским; вектор электрического поля лежит в плоскости, проходящей через вектор направления на источник сигнала ф0 и ось, ортогональную Oz .
При длительности радиоимпульса т >> a 0 / с ,
новое сопротивление свободного пространства. Выражения для расчета поляризационных компонентов рассеянного поля по распределению токов объекта приведены в [11].
Тангенциальная составляющая электрического поля облучающего прямоугольного радиоимпульса на поверхности рассеивателя имеет вид
E tg ) ( z , ф, t ; ф 0 ) =
Е 0 cos I © 0 I t —
—
где c
–
скорость света, поверхностному току
кольца в каждый момент времени t сопоставим эквивалентный ток I 0 ( ф, t ) на элементарном участке окружности радиуса R 0, поверхностный заряд будем характеризовать распределением q 0 ( ф, t ) в секторе углов ф е [ —А; А ] . Поверхност-
ные токи
отрезков представим эквивалентными
осевыми токами I к ( z , t ) , к = 1,2, удовлетворя-
/-V ющими граничным условиям Ik
= 0,
а заряды
–
удельными плотностями q k ( z , t ) ,
к = 1, 2. Амплитуды реальных и эквивалентных токов и зарядов, как показано в [6], отличаются на малую величину порядка O ( a 0 ) ; смещением их зависимостей от времени на АТ 0 = a 0 / можно пренебречь, поскольку Ат 0 << т.
Энергетическая ДР объекта определяется выражением [7]
х ( ф; ф 0 )
D (ф ; ф0 )= - , max X (ф; ф0)
ф
где
ю х (ф; ф0) = J хt (ф, t; ф0) dt
—ю
<
4 R 0 2 sin c
2 Г ф — ф 0
1 I
9 , ,
:2 1 + ^ 0 I,
–
угловая зависимость плотности потока энер-
гии отраженного поля,
X t ( ф, t ; ф 0 ) = ^4^ lim r 2 l EE ( r , ф, t ; ф 0 ) 2 W 0 r ^ю
–
угло-временное распределение плотности по-
тока рассеиваемой в пространстве энергии, |ЕЕ ( r , ф, t ; ф 0 )| — квадрат модуля текущего зна-
–
чения амплитуды рассеянного поля, вычисляемый как сумма квадратов текущих значений азимутальной ЕЕ ф ( r , ф, t ; ф о ) и меридиональной Е q ( r , ф, t ; ф о ) составляющих вторичного излучения в дальней зоне элемента [4; 11], W 0 – вол-
т
—
0,
t
11;
т
t > -, 2
где E 0 ,
–
амплитуда, циклическая ча-
стота несущей и начальная фаза импульса; для радиоимпульса с гауссовской огибающей ее величина определяется выражением
E tg ) ( z , ф, t ; ф 0 ) =
= Е о exp
(
2т 2
Г 1 2 - :
t --/4 R 0 sin с N
2 Г ф — ф 0
1 I
п2) 2
х(5)
L L 1
х cos © 0 t --Л 4 R 0 sin с V
2 Г ф —ф 0 " I 2
^ ^
.
Используя определение векторного и скалярного потенциалов [11], напряженности электрического поля тонких трубчатых объектов [5; 6] c учетом калибровки Лоренца [4; 11] для их электродинамических потенциалов, запишем систему ИДУ с пространственно-временными операторами для I 0 ( ф, t ) , q 0 ( ф, t ) и I к ( z , t ) , q к ( z , t ) , к = 1, 2:
G 00 (ф , t ) + 2 Q 0 к (ф , t ) = E 0 (ф , t ) ;
к = 1
p 00 ( ф, t ) + 2 v 0 n ( ф, t ) =0; ф е[—А ; А] ;
<
n = 0
G 10 ( z , t )+ 2 Q i к ( z , t ) = E 1 ( z , t ) ;
к = 1
р ю( z , t ) + 2 V 1 n ( z , t ) =0; z e l n = 0
G 20 ( z , t ) + 2 Q 2к ( z , t ) = E 2 ( z , t ) ;
к = 1
;
P 20 ( z , t ) + ^ V 2n ( z , t ) = °; z e [ °; l o ] , n = 0
P 00 ( ф, t ) =
где
д
R o дф
A I, ф', t
-
A R 00
c
I
a A ^l ф', t
G 00 ( ф, t ) =r 4п д t
^^^^^^B
A R 00
l
-A
-------c - d ф' + A R 00
д
+-- д t
e
A -
A ф', t -
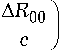
+
1 д
4 лб 0 ^ 0 дф
e
A qi
-A
ф', t -^R 00 ) c -
A R 00
d ф',
-A
A R 00
– тангенциальная составляющая электрическо-
го поля кольца, создаваемого его токами и за-
рядами,
a A ^1 Ф'’ t
Gs 0 ( z , t ) = ^ - s 0 v ’ 4пд t
A R
-
s 0
-A
c
AR 0
d ф' +
+
1 д_
4 лб 0 д z
A q 0 1 ф , t--s I
A c-^ d ф',
- J A Rs 0
s = 1, 2,
– тангенциальные составляющие
электрическо-
го поля отрезков, создаваемого токами и заря-
дами кольца,
Q 0 k ( Ф, t ) =
= Ц 0 д
4п д t
l o + ( - 1 ) k l o 22
I
- l 0 + ( - 1 ) kl 0 22
—w I
I k l z ', t
-
A R 0 k
A R 0 k
c —- dz ' +
д
+---
4 лб 0 R 0 дф
l 0 + ( - 1 ) kl 0 22
I
- l 0 + ( - 1 ) kl 0 22
f AR q k l z t--0k
a R 0 k
c —- dz ',
k = 1, 2
–
тангенциальная составляющая электрическо-
го поля кольца, создаваемого токами и заряда-
ми отрезков,
Q sk ( z , t ) =
= Ц 0 д
4п д t
l 0 k l 0
2 +( 1 ) 2 Ik z ', t
I 1
/-V
1д
+---
4 лб 0 д z
-
- l 0 + ( - 1 ) kl 0 22
l 0 + ( - 1 ) kl 0
I
-
- l 0 + ( - 1 ) kl 0
A Rs k
dz' +
q k l z , t
A R sk
dz ',
s = 1, 2, k = 1, 2
– тангенциальная составляющая электрического поля отрезков создаваемого их токами и зарядами
A R 00
d ф',
d ф' +
P s 0 ( z , t )
a A I0l ф',t д az J
-A
-
a R s 0
c
A R s 0
d ф' +
f A R )
дA q0 h t- ^s0 L, + d ф, д t _JA A Rs 0
s = 1, 2
–
слагаемые выражения для калибровки Ло-
ренца [4; 11] электродинамических потенциалов
разомкнутого кольца и s -го присоединенного
отрезка ( s = 1, 2),
рядами,
V 0 k ( ф, t ) =
д
R o дф
создаваемых их токами и за-
l o + ( - 1 ) kl 0
I
- l 0 + ( - 1 ) k 1 0
I k l z , t
-
A R 0 k
A R k 1
—-—- dz ' +
2 +И k l 2
+- д t J
- 1 0 + ( - 1 ) k l 0
k = 1, 2,
_ f A R
<1 k l z , t --0 k
A R 0 k
c —- dz' ,
Vsk ( z , t ) =
д
д z
д
+ — д t
l 0 + ( - 1 ) k 1 0 22
I
-
- l 0 + ( - 1 ) kl 0
l 0 + ( - 1 ) kl 0
I
-
- l 0 + ( - 1 ) kk 22
^* /
I k l z , t
A R sk
dz ' +
q k z , t
A R sk
dz ,
s = 1, 2, k = 1, 2
– слагаемые выражения для калибровки Лоренца электродинамических потенциалов зеркально-асимметричного элемента, учитывающие электромагнитное взаимодействие [10] кольца и присоединенных к краям его разрыва отрезков,
Ё 0 ( ф, t ) = E tg ) ( 0, ф, t ; ф 0 ) ,
E k ( z , t ) = E tg ) ( z , ( -1 ) k A, t ; ф 0 ) , (15)
k = 1, 2
– касательные возбуждающего поля на поверхности кольца и отрезков,
J . . 9 I Ф
4 R o sin I
-ф'
+ a 0 ,
В результате система ИДУ (6) преобразуется в систему 2 ( N 0 + 2 N ) линейных алгебраических уравнений для m -го шага по времени, m = 1 — M ,
A Rs 0 = 4 R 2 sin'
( , ( s +1 A A
2 ф' + ( -1 ) A
+ z 2 ,
s = 1, 2,
A R 0 k = 4 R 2 sin
( ( k + 1
2 Q+j-1)^
+ ( z^ ,
k = 1, 2,
A R ss = V ( z — z ') + a 2 , s = 1, 2,
A Rsk = 4 R 2 sin 2 A + ( z - z ' ) 2 ,
s = 1, 2, k = 1, 2, s й k
– расстояния между точками интегрирования на осевой линии и точками наблюдения на поверхности элемента в (7) — (15), S o и Ц о — диэлектрическая и магнитная проницаемость вакуума.
Для численного решения системы ИДУ (6) применим метод Гаусса [12] при последовательном продвижении по времени [5; 6] c аппроксимацией зависимостей I 0 ( ф, t ) и q o ( ф, t ) произведением кусочно-постоянных функций
J1 при ф е n Аф, n Ф [0 при фй n Аф, (17)
n = 1 — N 0, где Аф — интервал дискретизации поверхности кольца, и
Г1 при t е m A t , Y m ( t ) = I
[0 при t й m A t ,
m = 1 — M ,
где A t — шаг по времени с весовыми коэффициентами a nm и в nm , n = 1 — N 0 , m = 1 — M соответственно; распределение I к ( z , t ) и q k ( z , t ) , k = 1, 2, разложим по базису функций
f (k) (z) = J1 при z е n Az’ n [0 при z й n Az, k = 1, 2, n = 1 — N,
где A z — интервал дискретизации присоединенных отрезков и (18) с весовыми коэффициентами 5 nm и в nm , n = 1 — N , m = 1 — M • Частные производные искомых токов и зарядов в (6) по ф и t вычисляются с использованием разностных схем [5; 6].
a л (0) + XXj^k y(^k рm рm рm
+у [ x ( 0 k )+ У ( 0 k )l = v(0 )
+ | pm + pm I Y pm, k=1
a © (0) + X ( 22 ) Y( 00 )
pm V / pm + pm +
R0 Aq
+ z [ x pm ) + k = 1
< p = 1 — N 0 ,
x ( q 0) + y( q 0 ) gm 1 gm
A t
У(0 k)! = Q pm I , m = 1 — M,
+
+ X [a k' ' qk 1 (0 ) + X * > + Y ( m > ] = r gm , k = 1
x ( q 0 ) + v( q 0 ) + gm + gm +
+z
k = 1
-( k ) ~( qk ) y( qk ) y( qk ) "
a gm^ (u) + gm + x gm
A z
A t
= 0,
[ q = 1,2,
где
g = 1 — N , m = 1 — M ,
N 0
Xnm = ^ 5 j,m-|n—j| A(|n - j|)- j=1, m-| n - j >0
-
N 0
z
j = 1, m - 1 -| n - j | > 0
a
j , m -1-| n - j|
тЛ (| n
-
j D,
n = 1 — N 0, m = 1 — M ,
N 0 - 1
у(00) = у в nm / A в j=1, m-1-| n+1-j| >0
j , m - 1 - n +1 - j|
•w
fl (I n + 1 - j I)
-
N 0 - 1
- E в и (in - j), ^^ j, m-1-|n - j j=1, m-1-| n - j| >0
n = 1 — N 0 , m = 1 — M ,
– выражения для расчета тангенциальной составляющей вторичного электрического поля кольца (7) в N 0 точках поверхности для M от-
счетов по времени по дискретным значениям
a nm и в nm , n 1 — N 0 , m 1 — M ,
MN
y( 0 k ) Ц 0 v V й( k ) [ ( k ) +
X nm 4 n a t /z 5 g j I/ gn jm g = 1 j = 1
- г(k )• gnjm
k = 1, 2, n = 1 — N 0, m = 1 — M ,
y(0k) =-----1----- nm 4ле0 R0A»
MN
ZZ - ( k U gnjm
I—
_ и ( k ).
gnjm
g = 1 j = 1
- (24)
k = 1, 2, n = 1 ^ N 0 , m = 1 ^ M
– выражения для расчета тангенциальной составляющей вторичного электрического поля кольца (9), наведенного токами и зарядами k -го отрезка, k = 1, 2, в N 0 точках поверхности в M моментов по времени,
– выражения для расчета тангенциальной составляющей вторичного электрического поля k -го отрезка (8), создаваемого токами и зарядами кольца, в N точках поверхности для M отсчетов по времени по a nm и в nm , k = 1, 2, n = 1 ^ N , m = 1 ^ M ,
N
v( qk) = У nm /
X (00J = nm
N 0
N 0 - 1
z j=1, m-1-| n+1-j| >0
- 1
a
•w
-
-
m
N z j = 1’
j = 1, -| n - j l > 0
(k) a j,m
(k) a j,m
-
,Л( qk ) (I n - , 1)
1 I Л ( qk )(| n - j ),
• 1- n - j
-
-
z
, j = 1,
/-V
a j, m-1-n - j\
m - 1 -| n - j | > 0
n = 1 ^ N 0 , m
N 0
Y (00) = У nm =
m - 1 -| n - j | > 0 q , k = 1, 2, y( qk ) = Y nm
n = 1... N ,
m = 1... M ,
= 1... m ,
в
/-V
-
> -
-
j = 1, m -| n - j | > 0
N 0
в j,m j=1, m-1-| n - j| >0
-
-
, ® 1-1 n - j l
n = 1 ^ N 0, m = 1 _ M
–
квадратурные суммы подынтегральных выра-
жений [12] в (11), получаемые при замене эквивалентного тока на элементарном участке и заряда кольца множеством значений a nm и - nm , n = 1... N 0 , m = 1... M ,
x ( 0 k ) nm
MN
^4tv- zz a 4^6 0 R 0 A » g = 1 ^
.( k ) Гг( k ) + gnjm
gj
-
( k ) - gnjm
-’(27)
k = 1,
2, n = 1... N 0, m = 1... M ,
у ( 0 k ) nm
k = 1,
MN
= ^ \ yp ( k )y ( k )+ _u(k ) - 1
4n atz^-gjgj L gnjm gnjm-’ g=1 j=1
2, n = 1 ^ N 0, m = 1 _ M
– представление (13) при замене эквивалентно-
го тока и удельной плотности заряда k -го от-
( k ) и в nm ,
резка, k = 1, 2, множеством значений a n = 1... N , m = 1... M ,
( k )
nm
X ( k 0 ) nm
M N 0
^ 0 у Yn Г ( k ) + 4n A t Zz gj L gnjm g = 1 j = 1
-
L ( k ) 1 gnjm --,
k = 1,
2,
n = 1... N 0, m = 1... M ,
v( к 0 ) nm
M N 0
—1— ZZ₽ gj H 4”= 0 R 0 A » , ~ 1 z L
■( k )+ gnjm
-
H ( k ).
gnjm
- (30)
k = 1,
2, n = 1 ^ N 0 , m = 1 ^ M
N - 1 z j = 1, m - 1-| n + 1 - j | > 0
N - 1
в ( k )
P j , m - 1-| n + 1 - j|
n < qk )(| n +1 - j )
-
У в ( k ) 1 I .|Q( qk )(| n - j ) ,
Z-^ j ’ m-1- n - j j=1, m-1-| n - j| >0
q , k = 1, 2, n = 1... N , m = 1... M
– выражения для расчета тангенциальной составляющей вторичного электрического поля k -го отрезка (10) при замене их эквивалентных токов и удельной плотности зарядов множеством значений a nm и в nm , k = 1, 2, n = 1 ^ N , m = 1 _ M ,
x ( k 0 ) nm
k = 1,
у ( к 0 ) nm
k = 1,
–
M N 0
4 ^*5» z z “ gj L L gnjm
2, n = 1... N ,
m = 1... M ,
M N 0
4^ zz - gj Г H
g = 1 j = 1
-
L ( k ) - 1
gnjm J’ (33)
■( k )+ gnjm
-
rj ( k ) - H gnjm ’
2, n = 1... N , m = 1... M
вид (12) при представлении эквивалентного
тока на элементарном участке и заряда кольца
дискретными m = 1... M,
( qk )
nm
m -:
значениями a nm и в nm , n = 1 ^ N 0 ,
N
z j=1’
1-| n + 1 - j | > 0
N
( k )
a j, m-1-| n+1-j|
-
-
у a( k )
Z j, m-1-| n - j| j=1, m-1-| n - j| >0
q , k = 1, 2, n = 1... N 0, m = 1... M ,
N y?kk)= z вjk)-n -j®qk)(in - j)- j=1, m-| n - j |>0
N
- z в jkm . i-i - - л ®* qk ) d - - j ) , (36)
j=1, m-1-| n - j >0
m = 1 — M ,
Y nm = E 0 ( n Аф, m A t ) , n = 1 — N 0 , m = 1 — M ,
Y ( nm = E k ( n A z , m A t ) , k = 1, 2, n = 1 — N , m
1 — M ,
– элементы вектор-столбца удельных эквивалентных потенциалов, определяемые значениями комплексной амплитуды возбуждающего поля (15) в N 0 точках на поверхности кольца и в N точках на поверхности k -го присоединенного отрезка, k = 1, 2, на m -м интервале времени, m = 1 — M ,
Л d n - j I)= ^"A- j ) , n , j = 1 - N 0 (39)
– элементы матрицы удельных импедансов элементарных участков кольца,
Q (I n - j |) =_® ^ n . j l) , n , j = 1 — No (40)
4 лб 0 R0 Аф 0
– элементы матрицы обращенных емкостей элементарных участков кольца,
(qk) ^0®(qk) (In - jI)
Л n - j =---------------, n , j = 1 — N (41)
4nA t ’
- элементы матрицы собственных (при q = k ) и взаимных (при q ^ k ) удельных импедансов присоединенных отрезков, q , k = 1, 2,
® ( qk ) (l n - j I)
Q ( qk ) ( n - j ) =—3 ) , n , j = 1 — N 0 (42)
4n s0A z
– элементы матрицы обращенных собственных (при q = k ) и взаимных (при q ^ k ) емкостей отрезков, q , k = 1, 2,
(k)± = gnjm
A R 0 k ф= n Aф / c I / A R 0 k ф= n Aф dz ,
(k)± gnjm
2 + ( - 1 ) kl 0 + g A z
J Y m [ ( j - m - 0,5 ) A t -
- 2 + ( - 1 ) kO + ( g - 1 ) a z
- A R 0 k ф= ( n ± 0,5 ) Аф / С I / A R 0 k ф= ( n ± 0,5 ) Аф dz ', (44)
g = 1 — N , n = 1 — N 0, j , m = 1 — M , k = 1, 2;
( g + 0,5 ) Аф
Lk njm = J Y m К j - m ± 0,5 ) A t -
( g - 0,5 ) Аф
- A R k 0 I z = n A z / c I / A R 0 k l z = n A z d ф ,
g А Ф
Hk ± m = J Y m К j - m - 0,5 ) A t -
( g - 1 ) А Ф
- ARk0 |z=(n±0,5)Az / c] / AR0k |z=(n±0,5)Az dф‘, g = 1 — N 0, n = 1 — N, j, m = 1 — M, k = 1, 2
– вспомогательные функции для расчета взаимных удельных импедансов и обращенных емкостей кольца и k -го присоединенного отрезка, k = 1, 2,
(S ( n - j )
V a 0 + 4 R 0
X
F
r ( arcsin
V V
A A
2 R 0
V a 0 + 4 RO v a0 + 4Ro sin фn-j
a
0
+
4
R
O
sin
2
n
-
j
-
F
arcsin
V
a
0
+
4
R
O
sin ф|
n
-
j
a
0
+
4
R
o
sin
2 ф|
n
-
jj
V
a
0
+
4
R
o
?
2
R
0
ф
l±-
j
=(l
n
-
j
±0,5
)Аф
– вспомогательная функция для расчета удельных импедансов и обращенных емкостей элементарных участков кольца [13],
®
(
qk
)(|
n
-
j
h =
=
ln
Рис. 1.
Энергетическая ДР
D
(
ф
;
ф
о
)
элемента, облучаемого радиоимпульсом с прямоугольной огибающей с направления
ф
о
=
О
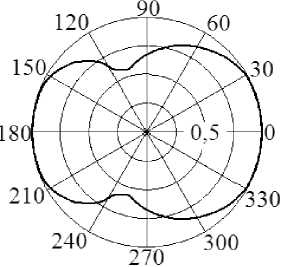
Рис. 2.
Энергетическая ДР
D
(
ф
;
ф
о
)
элемента, облучаемого радиоимпульсом с гауссовской огибающей с направления
Ф
о
=
0
(|
n
-
j
+ 0,5) + ^(|
n
-
j
I + 0,5)
2
+ (^
qk
/А
z
)
2
(|
n
-
j
I - 0,5) + ^(|
n
-
j
| - 0,5)2 + (^
qk
/А
z
)
2
– вспомогательная функция для расчета собственных (при
q
=
k
) и взаимных (при
q
*
k
) удельных импедансов и обращенных емкостей, присоединенных отрезков,
„ = J а о при q = k, qk [ Ro sin А при q * k, q, k = 1, 2
— символьная переменная,
F
(
к,
p
)
— эллиптический интеграл первого рода [12].
Для решения системы уравнений (20) шаг Аt определялся по теореме отсчетов В.А. Котельникова [14] для верхней границы эквивалентной полосы циклических частот [10] облучающего радиоимпульса; интервал дискретизации кольца по азимутальной координате удовлетворял соотношению Аф = с Аt/Ro , а интервал дискретизации присоединенных отрезков – соотношению Аz = с Аt. Согласно [5; 6], при выбранных значениях Аt, Аz и Аф достигаются стабилиза- ция разностных схем вычисления производных и сходимость последовательностей, аппрокси- мирующих распределение токов и зарядов рас- сеивающего элемента. Ввиду того, что эквивалентные токи I k (z, t) , k = 1, 2, обращаются в нуль при z = (-1)k lo, k = 1, 2, коэффициенты —w a
(
k
)
nm
,
n = 1... N, m = 1... M, рассчитывались в центральных точках интервалов Аz, а значе-
S
(
k
)
ния вnm, n = 1... N, m = 1... M, — в точках, сме-
щенных вдоль продольных осей присоединенных отрезков на А
z
/2 и по оси времени на А
t
/2. Весовые коэффициенты a
nm
и в
nm
,
n
= 1...
N
о
,
m
= 1...
M
, вычислялись при различии значений азимутальной координаты на Аф/2 и смещении моментов времени на А
t
/2 [13].
По найденному распределению эквивалентных токов и зарядов в соответствии с [11] вычислены асимптотические (при
r
^ да) значения поляризационных компонентов вторичного поля элемента
E
ф
[
q
]
(
r
, ф,
t
; ф
о
)
и путем последовательной подстановки полученных результатов в (3), (2) и (1) рассчитана его энергетическая ДР.
На рис. 1 приведена энергетическая ДР зеркально-асимметричного элемента с относительными размерами
lo /R
o
= 0,85,
a
o /
R
o
= 0,01 и 2А = п /15, облучаемого прямоугольным радиоимпульсом длительности т = 6,25
R
o /
с
с циклической частотой to
o
= 2л/т и начальной фазой Ф
О
= 0 с направления ф
о
= 0; на рис. 2 представлена энергетическая ДР элемента, возбуждаемого сигналом с гауссовской огибающей и указанными выше частотно-временными параметрами при ф
о
= 0.
Из полученных результатов следует, что по аналогии с монохроматическими процессами [1; 8] импульсные сигналы, переизлученные зеркально-асимметричным объектом, имеют анизотропное распределение в плоскости азимута. Угловое положение максимума энергетической ДР элемента, возбуждаемого прямоугольным радиоимпульсом с внешней стороны разрыва кольца, противоположно направлению на источник излучения. Плотность потока энергии сигнала, рассеянного в направлении ф = п, не превышает 25 % относительно значения для ф = 0. Уровень энергетической ДР элемента, облучаемого радиоимпульсом с гауссовской огибающей, эквивалентная длительность которого, как показано в [13], составляет 1,2. „ 1,35т, в направлении ф = п ниже на 1,3 дБ вследствие уменьшения электрических размеров объекта по сравнению со случаем возбуждения прямоугольным радиоимпульсом. Установлено, что за счет увеличения ширины разрыва кольца 2А = п /15 в 3 раза глубина про- вала энергетической ДР элемента, облучаемого прямоугольным радиоимпульсом длительностью τ =7,12 R0 c, возрастает на 1,2 дБ. Смена направления прихода сигнала ϕ0 =0 на противоположное приводит к изменению угловой зависимости вторичного излучения в плоскости азимута, характерному для ДР только планарных зеркально-асимметричных элементов, возбуждаемых монохроматической волной [1]. При возрастании τ в 5…7,5 раз уровень энергетической ДР элемента, приведенной на рис. 1, в направлении ϕ=π убывает на 2,2…2,5 дБ.
За счет уменьшения относительной длины отрезков до
l
0
R
0= 0,35 при неизменных значениях других размеров элемента и параметров облучающих радиоимпульсов уровень вторичного поля в направлении ϕ=π снижается на 3,8…4,3 дБ. В энергетической ДР разомкнутого кольца (
l
0
R
0= 0) при ϕ=π формируется провал [13], глубина которого по мере увеличения циклической частоты несущей облучающего сигнала в 1,5…2,5 раза возрастает примерно на 1,2…1,5 дБ. По мере уменьшения длительности радиоимпульса τ=6,25
R
0
c
в 1,3…1,5 раз глубина провала энергетической ДР кольца убывает при снижении плотности потока энергии вторичного излучения в направлении ϕ=0 на 2,1…2,2 дБ [13].
Таким образом, на основе численного решения ИДУ с пространственно-временными операторами для эквивалентных осевых распределений токов и зарядов проведен анализ вторичного излучения радиоимпульсов зеркально-асимметричным элементом в виде разомкнутого кольца с перпендикулярными его плоскости отрезками на краях разрыва. Исследовано влияние аналитических свойств огибающих и частотно-временных параметров облучающих сигналов на энергетическую ДР объекта.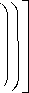
Список литературы Рассеяние радиоимпульсов на разомкнутом тонком кольце с перпендикулярными его плоскости отрезками на краях разрыва
- Неганов В.А., Градинарь И.М. Электродинамические свойства тонкопроволочных бианизотропных частиц для метаматериала // Физика волновых процессов и радиотехнические системы. 2011. Т. 14. № 3. С. 31-37.
- Simonovsky C.R., Belov P.A., He S. Backward wave region and negative material parameters of a structure formed by lattices of wires and split-ring resonators // IEEE Transactions on Antennas and Propagations. 2003. Vol. 31. № 10. P. 2582-2591.
- Веселаго В.Г. Электродинамика веществ с одновременно отрицательными значениями e и m // Успехи физических наук. 1967. Т. 92. Вып. 3. С. 517-526.
- Неганов В.А., Павловская Э.А., Яровой Г.П. Излучение и дифракция электромагнитных волн / под ред. В.А. Неганова. М.: Радио и связь, 2004. 264 с.
- Schuman H. Time-domain scattering from a nonlinearly loaded wire // IEEE Transactions on Antennas and Propagation. 1974. Vol. 22. № 5. P. 611-613.
- Стрижков В.А. Моделирование переходных электромагнитных процессов в вибраторных Антенных решетках //Антенны. 2006. № 11(114). С. 50-55.
- Кенно Е.М., Моффатт Д.Л. Аппроксимации переходных и импульсных переходных характеристик // ТИИЭР. 1965. Т. 53. № 8. С. 1025-1034.
- Неганов В.А., Осипов О.В. Отражающие, волноведущие и излучающие структуры с киральными элементами. М.: Радио и связь, 2006. 280 с.
- Васильченко О.В. Пространственно-временная обработка сверхширокополосных сигналов в радиолокационных станциях с электронным сканированием диаграмм направленности антенн. Смоленск.: Военная академия войсковой ПВО Вооруженных Сил РФ, 2011. 114 с.
- Активные фазированные антенные решетки / под ред. Д.И. Воскресенского, А.И. Канащенкова. М.: Радиотехника, 2004. 488 с.
- Самсонов А.В. Макроскопическая электродинамика. Вопросы теории пространственно-временных преобразований. М.: Радиотехника, 2006. 64 с.
- Фильчаков П.Ф. Справочник по высшей математике. Киев: Наукова думка, 1972. 743 с.
- Разиньков С.Н., Разинькова О.Э. Рассеяние радиоимпульсов на разомкнутом идеально проводящем кольце // Физика волновых процессов и радиотехнические системы. 2013. Т. 16. № 4. С. 45-49.
- Догадин Н.Б. Основы радиотехники. СПб.: Лань, 2007. 272 с.


