Рассеяние света многослойным цилиндром в приближении Вентцеля-Крамерса-Бриллюэна
Автор: Шаповалов К.А.
Журнал: Пространство, время и фундаментальные взаимодействия @stfi
Рубрика: Оптика
Статья в выпуске: 3 (24), 2018 года.
Бесплатный доступ
Получены формулы для амплитуды светорассеяния, факторов эффективности ослабления и поглощения многослойного кругового цилиндра в приближении Вентцеля-Крамерса-Бриллюэна (ВКБ) в скалярном виде при падении света перпендикулярно оси цилиндра. Проведено численное сравнение факторов эф- фективности ослабления и поглощения в приближении ВКБ конечного двухслойного цилиндра с резуль- татами расчета для бесконечно длинного двухслойного цилиндра (строгое решение методом разделения переменных). Получено хорошее согласие в области применения приближения ВКБ.
Рассеяние света, факторы эффективности, приближение вентцеля-крамерса-бриллюэна
Короткий адрес: https://sciup.org/142216022
IDR: 142216022 | УДК: 535.36 | DOI: 10.17238/issn2226-8812.2018.3.54-61
Текст научной статьи Рассеяние света многослойным цилиндром в приближении Вентцеля-Крамерса-Бриллюэна
В оптике аэрозолей, биологических взвесей, коллоидной химии для быстрого анализа, характеристик светорассеяния частицами произвольной формы и структуры используются различные приближения [1-6]. Если светорассеивающие частицы оптически «мягкие» (|т — 1| << 1, где
-
1 E-mail: sh const@mail.ru
т = п + г% относительный показатель преломления частицы), то чаще применяют приближения Рэлея-Ганса-Дебая (РГД), Вентцеля-Крамерса-Бриллюэна (ВКБ), и Аномальной Дифракции (АД). В приближении РГД и АД получены формулы для характеристик светорассеяния многослойных сферических частиц, сфероидов, эллипсоидов, которыми обычно моделируют клетки и биологические частицы [2-7].
Целью настоящей работы является анализ светорассеяния многослойными цилиндрическими частицами в приближении ВКБ. Ранее автором показано аналитически [8], что выражения для фактора эффективности ослабления однородной частицы любой формы в приближениях ВКБ в скалярном виде и Аномальной дифракции (АД) совпадают с точностью до знака %. Поэтому полученные далее формулы для фактора эффективности ослабления ВКБ могут быть полезны и для приближения АД.
1. Амплитуда светорассеяния в приближении ВКБ и РГД
Предположим, что на коаксиальный многослойный цилиндр высоты Н и внешнего радиуса R n состоящий из N слоев, падает плоская электромагнитная волна в плоскости ZOY прямоугольной системы координат под углом 6i к о си z (рис. 1), каждый j-слой радиуса Rj имеет собственный относительный показатель преломления mj (по отношению к внешней среде).
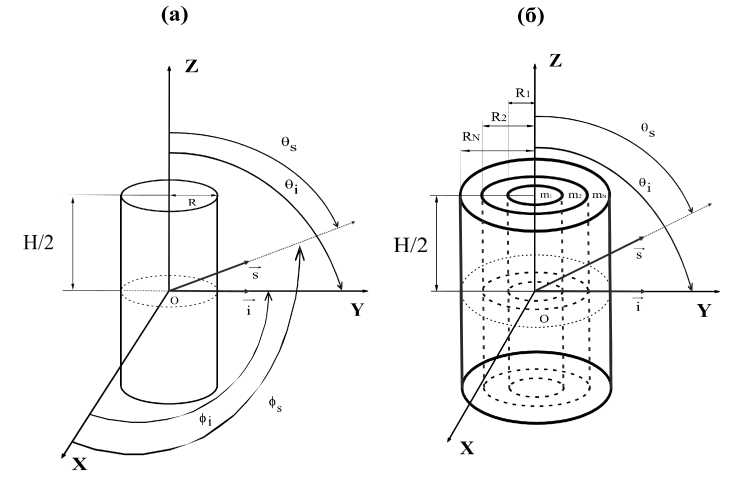
Рис. 1. Геометрия светорассеяния однородным (а) и многослойным круговым цилиндром (б) высоты Н.
Используем интегральное представление амплитуды светорассеяния в приближении ВКБ и РГД [8, 9]:
к2
f ( s , i ) = 4Z [- s x ( s x e i)] J (m
— 1)T exp [гк (A(m — 1)( r • i — ^1) + r ( i — s ))] dV,
где s , i — единичные векторы вдоль направления рассеяния и распространения света соответственно, £1 — входная координата на поверхности частицы для волны, проходящей через точку г, T = T(m,6i ) — коэффициент пропускания Френеля (причем T(т,^/2) = 2/(т + 1)), r — радиус-вектор точки внутри частицы, постоянный коэффициент A = {0,1} (A равен 0 и 1 для РГД и ВКБ приближений соответственно).
Тогда из (1) для амплитуды цилиндрической многослойной частицы (см. рис. 1 б) при 6i = ^/2
в скалярном виде ВКБ имеем [8]:
/ (s,i) =
R n z 2 y2
k2(m — 1) / [ f
------ exp ^ ^(m
- R n z1 y1
1)(y — y1 ) + "1ж + "2 У + "3z)] dydzdж,
где z1, z2, y1, y2 - входные и выходные координаты соответственно для z и y иа поверхности частицы, k1 = k[sin 9г cos фг — sin 98 cos фД, k2 = k[sin 9г sin фг — sin 98 sin ф8], k3 = k[cos 9г — cos 98 ], k'1 = k1, k'2 = k2 sin 9г + k3 cos 9г, k3 = k3 sin 9г — k2 cos 9г, 9г, фг, 9S, ф8 - углы, указывающие направление падающего и рассеянного света, в сферической системе координат.
Интегрируя (2), для оптически «мягкого» цилиндра (рис. 1 б), состоящего из N слоев (см. форм-фактор многослойных РГД частиц [2-4]), запишем амплитуду светорассеяния в скалярном виде в приближении РГД:
/ =
2тт
N -1
(mN — 1)VN F ( R n ) + ^ (md — mj+^VjF (Rj ) j=1
где k4 = V "2 + k2, F (ж) = 2A(7zA J1 (ж) _ функция Бесселя первого порядка, jo (ж) = sin^ -сферическая функция Бесселя нулевого порядка, Vj = ^R2H - объем j-oro слоя.
Для приближения ВКБ амплитуда, светорассеяния многослойного цилиндра, в скалярном виде выглядит более громоздко и не выражается через сумму форм-факторов слоев в отличии от приближения РГД.
2. Факторы эффективности светорассеяния, ослабления, поглощения
Сечение светорассеяния о8 по [9], нормированное на площадь S проекции частицы на плоскость, перпендикулярную оси пучка, (или фактор эффективности светорассеяния Q8) равно:
I = q8 = S у |/(s,z)|2dw, (4)
4~ где dw - элемент телесного угла (в сс[)ерической системе координат sin98d98dф8Y
Согласно оптической теореме [3], сечение ослабления ае, нормированное на площадь S проекции частицы в плоскости, перпендикулярной оси пучка, (или фактор эффективности ослабления Qe) равно:
Qe = "S = kSrm [f (i, i)] • ei. (5)
Сечение поглощения oa no [9], нормированное на площадь S проекции частицы в плоскости, перпендикулярной оси пучка, (или фактор эффективности поглощения Qa) равно:
I =Qa = S У ke" |E(r)|2 dV, (G)
V где E(r) - полное электрическое поле внутри частицы, е" = 2п\ ^ мнимая часть относительной диэлектрической проницаемости частицы (m2 = е" + гефф
Рассмотрим частный случай: падение света под углом 9г = ^/2 на однородный цилиндр радиуса R и высоты H вдоль оси Оу (рис. 1 а). Используя амплитуду светорассеяния (2), получим из (5) фактор эффективности ослабления в приближении ВКБ в скалярном виде [8]:
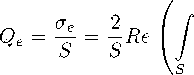
(1 — exp [г" (m — 1) (у2 — yi)]) dS^ , (7)
где yi, у2 - входные и выходные координаты соответственно для у на поверхности частицы.
Используя площадь S = 2RH и выражение (7), окончательно имеем [8]:
Qe90 = irStrHi (До),
где StrH1(x) - функция Струве первого порядка, До = 2kR(m— 1) - фазовый сдвиг «центрального» луча.
Заметим, что выражения для фактора эффективности ослабления в приближении ВКБ в скалярном виде (7) и (8) совпадают с таковыми в приближении АД [6].
Для многослойного (Д-слоев) цилиндра высоты H при падении света под углом 9г = ^/2 (см. рис. 1 б) факторы эффективности слоев не суммируются, по суммируется фазовый сдвиг от каждого слоя. Поэтому получим в приближении ВКБ фактор эффективности ослабления Qe90 в скалярном виде:
Qe90 = 2 — r —Re
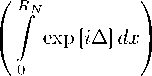
где Rj-1, Rj - радиусы внутреннего j — 1 и внешнего j слоев соответственно, имеющих относительные показатели преломления mj-1, mj, а Д = Д(х) - общий фазовый сдвиг, зависящий от положения х точки входа излучения
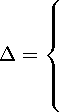
Д1 + ЕД Дj-1
Д, + ЕД+1 Дj-
ДN
0 < х < R1 ...
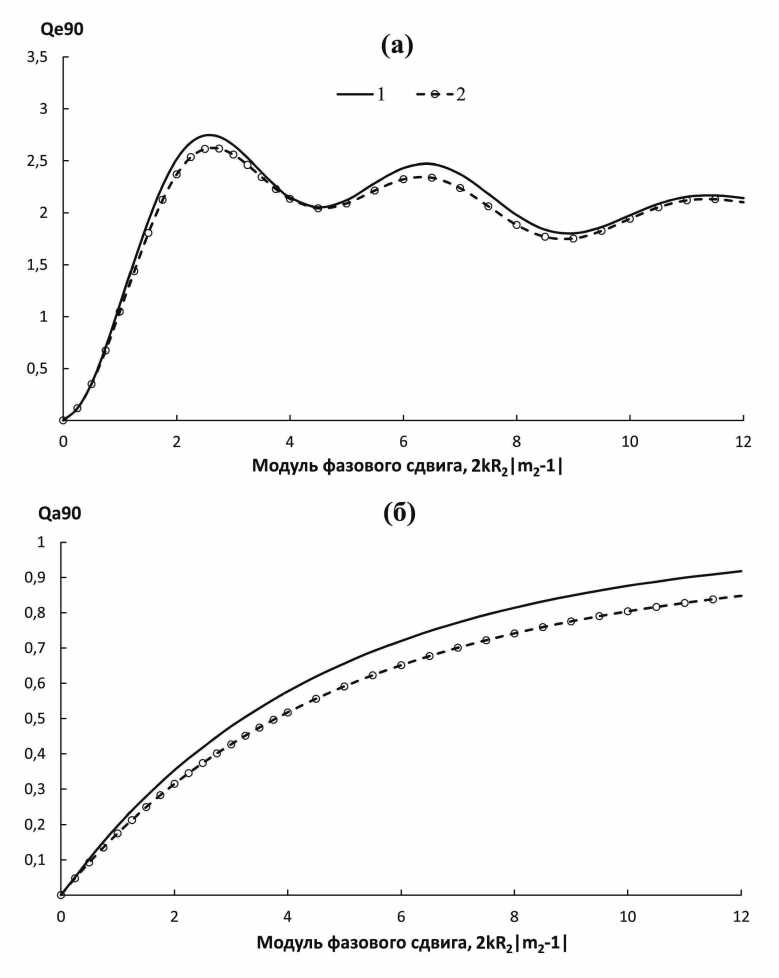
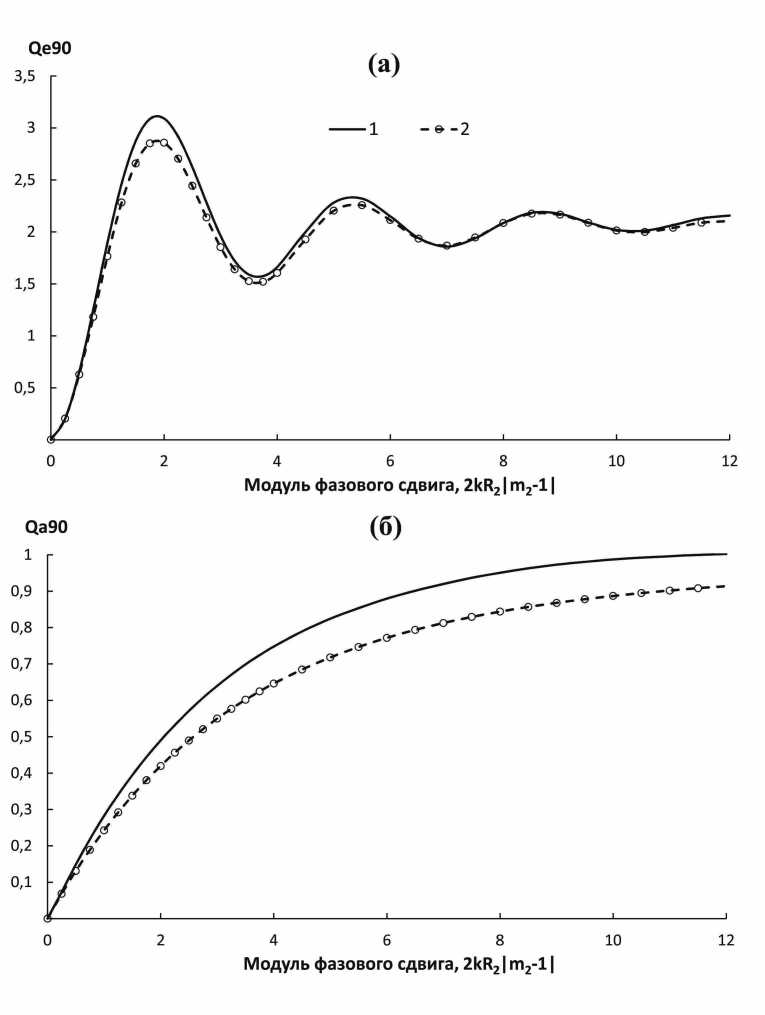
Rq-1 <Х Rj-1 < х < Rj Дj-1 = 2(mj — 1)к (УR2 — х2 — УR2-1 — х2) , Д1 = 2(m1 — 1)к^ R^ — х2, Д j = 2(m j — 1)к^ Rj — х2. Для двухслойного цилиндра с радиусом оболочки R2 и ядра R1 при падении света под углом 9^ = ^/2 в приближении ВКБ имеем из (9): Qe90 = 2 —RTRe где Д= { Д1 + Д12 Д2 0 < х < R1 R1 < х < R2 Д1 = 2(m1 — 1)k\jR2 — х2, Д2 = 2(m2 — 1)к<^R2 — х2, Vri—х2). Д2 = 2(m2 — 1)k I R R— — х"2 — В приближении ВКБ для фактора, эффективности поглощения из (6): Qa =2ких j |T(m, 9) |2 • exp [—2кх (у — У1)] dV, интегрирование по у (см. [8]) дает Qa = и j IT(m,9,)|2 • (1 — exp [—2кх (У2 — У1)]) dS. Таким образом, используя (11), получим выражение для фактора, эффективности поглощения однородного цилиндра радиуса R и высоты H в приближении ВКБ [8]: 4и ^ Qa90 = (и +1)2 +х2 1.2 (I1(4kRX)— L1 где Ii(x') = -г J1(ix) - модифицированная функция Бесселя 1 рода, Li(x) = -StT Hi(ix') - модифицированная функция Струве. В приближении ВКБ для многослойного (A-слоев) оптически «мягкого» цилиндра высоты Н при падении света под углом 9^ = ^/2 получим фактор эффективности поглощения Qa9o: 4nw (nw + 1)2 + xW Rn где A - общий фазовый сдвиг, зависящий от x также, как и в формуле (9). Очевидно, что фактор эффективности поглощения Qa90 в скалярном виде в приближении ВКБ (13) переходит в соответствующую формулу в приближении АД при условии достаточной оптической «мягкости» m ш 1, поскольку коэффициент 4nw/ ((nw + 1)2 + Xw) в (13) стремится к 1. Отметим также, что даже при падении света на цилиндр под углом близким к 9^ = ^/2 можно также использовать формулы для фактора эффективности ослабления Qe90 (9), (10) и поглощения Qa90 (13) в приближении ВКБ. после деления общего фазового сдвига. A на sin 9^. как и в приближении АД [6]. Решение для двухслойного бесконечно длинного цилиндра, получено ранее в [10-12]. Итак, для бесконечно длинного двухслойного цилиндра, при падении света, строго перпендикулярно оси цилиндра, имеем [П, 12]: an|| 0, ^nl 0, „ _ Jn(x2) [JX(m2X2) - AxYX(m2X2)] - m2 JX(X2) [Jn(m2X2) - AnY-nAm^^ an± — (1) (1) , HX (X2) [JX(m2X2) - AnY^(m2X2)] - m2H‘X) (X2) [Jn(m2X2) - AnYn(m2X2)] ^n|| = m2 Jn (X2) [JX (m2X2) - B YX (m2X2)] - JX (X2) [Jn (m2X2) - Bn Yn (m2X2)] m2Hn'! (X2) [JX (m2X2) - Bn Y^ (m2X2)] - H‘X) (X2) [Jn (m2X2) - B„ Y„ (m2X2)] An Bn m2Jn (m2Xi) Jn (mixi) - mi JX (m2Xi) J„ (miXi) m2Yn (m2Xi) JX (mixi) - miY^ (m2Xi) J„ (miXi) ’ m2Jn (miXi) JX (m2Xi) - miJX (miXi) Jn (m2Xi) m2YX (m2xi) Jn (miXi) - miYn (m2xi) JX (miXi)' где x1 = kRi- x2 = kR2- Jn(x). Yn(x) - функции Бесселя ii Неймана, целого порядка. hX^x) = = Jn (x) + iYn (x) - функция Гаикеля 1 рода. Факторы эффективности светорассеяния Qs, ослабления Qe и поглощения Qa запишем для двух поляризаций [3]: Qs|| = — ^о||| +2Y l6n||| ] Qe|| = XLRe ^о|| +2 Y &n||^ , QS^ - ∞ |по±|2 + 2 Y lanxi2 n = i Qex = -Re aox + 2 £ an± , X2 n=i 7 очевидно, для пеполяризоваппого света, в скалярном виде будем иметь _ Ое|£+Ое± _ Qs|| + QsX _ Qe 2 , Qs 2 , Qa Qe Qs- Далее нами проведено сравнение результатов расчета, факторов эффективности ослабления Qe90 и поглощения Qa90 для конечного двухслойного цилиндра высоты Н в приближении ВКБ по формулам (10), (13) и бесконечно длинного цилиндра. (16). На рис. 2 и 3 показаны зависимости величии фактора эффективности ослабления Qe90 и поглощения Qa90 от модуля фазового сдвига 2к R2|т2 — 1| для конечного в приближении ВКБ и бесконечно длинного двухслойных цилиндров (см. алгоритм в [11, 12]) с относительными показателями преломления слоев т1 = 1, 2 + г0, 02, т2 = 1,1 + г0, 01 при постоянных отношениях: R1 /R2 = 0, 5; R1 /R2 = 0, 9. Отметим, что значения фактора эффективности ослабления Qe90 и поглощения Qa90 в приближении ВКБ несколько ниже (не более 10%), чем соответствующие значения для бесконечно длинного двухслойного цилиндра (см. рис. 2, 3). Заключение Таким образом, получены выражения для факторов эффективности ослабления и поглощения в приближении ВКБ многослойного кругового цилиндра в скалярном виде при падении света перпендикулярно оси цилиндра. Также проведено численное сравнение факторов эффективности ослабления Qe90 и поглощения Qa90 для конечного в приближении ВКБ и бесконечно длинного двухслойных цилиндров. Отмечено неплохое согласие в области применения приближения ВКБ. Полученные выражения для факторов эффективности ослабления и поглощения в приближении ВКБ многослойного цилиндра могут быть обобщены в дальнейшем для произвольного угла падения света. Рис. 2. Зависимость величины фактора эффективности ослабления Qe90 (а) и поглощения Qa90 (б) от модуля фазового сдвига 2kR2|m2 — 1| в приближении ВКБ для конечного (2) и бесконечно длинного (строгое решение) (1) двухслойных цилиндров с относительными показателями преломления слоев т1 = = 1, 2 + г0, 02, m2 = 1,1 + г0, 01 при Ri/ R2 = 0, 5. Рис. 3. Зависимость величины фактора эффективности ослабления Qe90 (а) и пог лощения Qa90 (б) от модуля фазового сдвига 2kR2|m2 — 1| в приближении ВКБ для конечного (2) и бесконечно длинного (строгое решение) (1) двухслойных цилиндров с относительными показателями преломления слоев т1 = = 1, 2 + г0, 02, m2 = 1,1 + г0, 01 при Ri/R2 = 0, 9.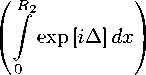
Список литературы Рассеяние света многослойным цилиндром в приближении Вентцеля-Крамерса-Бриллюэна
- Сидько Ф.Я., Лопатин В.Н., Парамонов Л.Е. Поляризационные характеристики взвесей биологических частиц. Новосибирск: Наука, 1990. 120 с
- Лопатин В.Н., Сидько Ф.Я. Введение в оптику взвесей клеток. Новосибирск: Наука, 1988. 240 с
- Борен К., Хафмен Д. Поглощение и рассеяние света малыми частицами. М.: Мир, 1986. 660 с
- Kerker М. The scattering of light and other electromagnetic radiation. New York, London: Academic Press, 1969. 666 p
- Шаповалов К.А. Рассеяние света частицами цилиндрической формы в приближении Рэлея-Ганса-Дебая. 1. Строго ориентированные частицы//Оптика атмосферы и океана. 2004. Т. 17. № 4. С. 350-353
- Ван де Хюлст Г. Рассеяние света малыми частицами. М.: ИЛ, 1961. 536 с
- Фарафонов В.Г. Рассеяние света многослойными эллипсоидами в Релеевском приближении//Оптика и спектроскопия. 2000. Т. 88. № 3. С. 492-494
- Шаповалов К.А. Рассеяние света произвольно ориентированным цилиндром в приближении Вентцеля-Крамерса-Бриллюэна. 1. Факторы эффективности ослабления и поглощения//Оптика атмосферы и океана. 2009. Т. 22. № 4. С. 321-324
- Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. М.: Мир, 1981. Т. 1. 280 с
- Кинг Р., Тай-Цзунь У. Рассеяние и дифракция электромагнитных волн. М.: ИЛ, 1962. 194 с
- Adey A.W. Scattering of electromagnetic waves by coaxial cylinders//Can. J. Phys. 1956. Vol. 34. № 5. PP. 510-520
- Kerker M., Matijevic E. Scattering of electromagnetic waves from concentric infinite cylinders//J. Opt. Soc. Am. 1961. Vol. 51. PP. 506-508


