Расщепление решений слабо нелинейных сингулярно возмущенных уравнений при регулярном вырождении

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

Асимптотическое поведение решений сингулярно возмущенных уравнений исследованы в работах [1–3]. В работе [4] проведен обзор развития теории сингулярно возмущенных уравнений с аналитическими функциями, а в [5] определены понятия погранслойные линии, области, регулярные и сингулярные области. Во всех перечисленных работах исследования проведены без расщепления решений. В данной работе решим задачу о возможности расщепления решений сингулярно возмущенных уравнений.

Постановка задачи

Пусть рассматривается уравнение гz'(t,г') = a(t)z(t,г) + гb(t) + sf (t,z(t,£)).                                (1)

с начальным условием

Z(t₀, г) = Z⁰,                                                       (2)

где 0 < г — вещественный параметр; t E D ^ С и D односвязная, открытая и ограниченная область, z(t,г') — скалярная функция, t = t 1 + it₂ , t 1 ,t₂ — действительные переменные, i = V—1, t₀ = t₁₀ + it₂₀.

Относительно правых частей (1) предположим выполнимость следующих условий:

• У1. a(t), b(t) E A(D} - пространство аналитических функций в области D.

• 1.    Для a(t) возможны различные случаи. В частности a(t) в области D может иметь конечное число нулей и полюсов. Для простоты рассмотрим только случай: У2. Yt E D (a(t) Ф 0).

• 2.    Задачу решим при условии У1, У2, У3, У4.

y3.f(t,0) = 0,f(t,x) E Q(H) где H = {(t,x),t E D, Ixl < M 1 } , здесь и далее буквами М 1 ,М₂... будем обозначать положительные постоянные не зависящие от г, причем |x⁰| <  M 1 .

y4.v((t,x),(t,x)) E H (|f(t,X) - f(t,x)\ < M 2 \x-^i\).

Задача. Расщепить решение задачи (1) – (2) на несколько составляющих и исследовать их асимптотическое поведение в области D.

Определение 1.Если выполняется условие У2, то будем говорить, что все точки области D являются простыми. Невозмущенное уравнение, соответствующее (1), имеет решение ^ = 0 и это решение не имеет особенностей.

Решение задачи

Решение задачи разделим на несколько частей.

• 1.    Расщепление решения.

В (1) введем новые неизвестные функции следующим образом

z(t, г) = n(t, г) + x(t, г),                                           (3)

где n(t, г),x(t, г) - новые неизвестные функции. (3) подставляя в (1) получим следующее уравнение:

гП ' (t,г) + гx'(t,г') == a(t)П(t,г) + a(t)x(t,г) + гb(t) + г(f(t,П(t,г') + x(t,г)')

Уравнение (3) расщепим на следующую систему (аргументы неизвестной функции будем опускать)

гП ' = a(t,}n +гf(t,П'),                                           (4)

n(t 0 ,     s) = x°,

ex' = a(t)x + cb(t) + e[f (t, П + %) — f (t, П)], x(t0,e) = 0.                                                  (5)

Далее займемся исследованием асимптотического поведения решений уравнений (4)-(5) с заданными начальными условиями. Для этого (4) – (5) заменим системой интегральных уравнений

П = x°exp

A(t)

e

+

}          ^A(t)—A(r)

I f (т , П) exp-------------ат, to

t

A(t) — A(r)

x = I [b(r)f(r, П + x) — f(T, n)]exp-----------dr, t0

где A(t) = C a(r)dr. Заметим, функция A(t) в точке t = t₀ имеет простой нуль. ^t 0

Прежде чем исследовать асимптотическое поведение решений (6)-(7) проведем некоторые геометрические построения.

Геометрические построения

Возьмем функцию A(t) и рассмотрим ReA(t), ImA(t).

Определение 2. Множество (p~) = {t Е D, ReA(t) = p — const} назовем линия уровня функции ReA(t).

Далее все геометрические построения будут проведены с использованием линии уровней функций ReA(t) и ImA(t).

Аналогично определяется линия уровня ImA(t), которую обозначим (q}.

Введем в рассмотрение линию уровня (p₀) = {t Е D, ReA(t) = 0}.

Поскольку A(t₀) = 0, то линия (p 0 ) проходит через точку t₀. Согласно У2 все точки D являются простыми т. е. функция A(t) в D не имеет кратных точек. Тогда через любую точку области D проходит единственная линия уровня функций ReA(t), ImA(t). Линии уровня, ReA(t), ImA(t), в точках пересечения взаимно ортогональны [6, 7]. Отсюда следует, область D покрывается сетью взаимно ортогональных линий уровня функций ReA(t), ImA(t) (Рисунок 1). Область D открытая, тогда существует сетка содержащая точку t₀ (Рисунок 2).

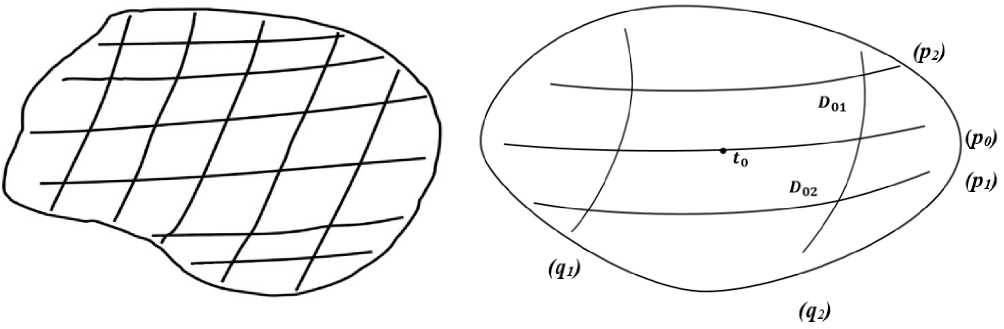
Рисунок 1. Покрытие области D

Рисунок 2. Сетка образованная линиями уровней (p), (q)

Сетку обозначим D₀. Линией уровня (р₀) сетка D разделяется на части D₀₁ и D₀₂ (Рисунок 2). На части линии (р₀) с D₀ возьмем произвольную точку t и проведем линию (q). Функцию ReA(t) рассмотрим вдоль (q). Известно [6, 7] вдоль (q) функция ReA(t) строго монотонна. Если учесть ReA(t) = 0, то справедливы следующие соотношения

(Vt е D₀₁ (ReA(t) < 0) Л Vtе D₀₂(ReA(t) >  0)) V V (Vt е D₀₁ (ReA(t) >0) Л Vt е D₀₂(ReA(t) <  0)),

Причем равенство имеет место только на границе (р0).

Поскольку полученные соотношения равнозначны, то не ограничивая общности будем считать

Vt е D₀₁ (ReA(t) < 0)Л Vt е D₀₂(ReA(t) > 0)

Для дальнейших исследований возьмем часть D₀₁ и выберем пути интегрирования для (6)-(7).

Vt е D₀₁ путь интегрирования состоит из части: (p₀)[t₀, t]; (q)[t, t]. Запись (l')[T₁, T₂] -означает                                 часть                                 кривой

• (l)    соединяющий точки T 1 и T₂. Отметим, по выбранным путям интегрирования ReA(t) не возростает. Определим линию уровня

(Р е ) = {t е D₀₁,ReA(t) = sins}.

Линия (р , ) разделяет область D₀₁ на части D Q1 , D0 1 , причем будем считать

• ⁽Р_£) е D^, (P q ) £ D^ (Рисунок 3).

  

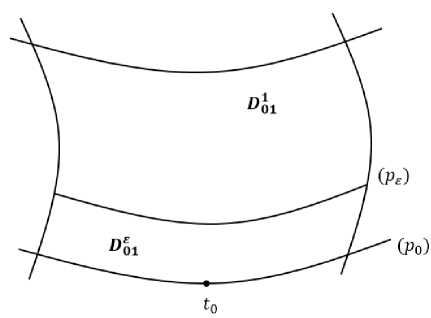
Рисунок 3. Области 0 01 ,0 01 .

Исследование асимптотического поведения решений уравнений (6) и (7)

Асимптотическое поведение решений уравнений (6)-(7) в области D₀₁ выражается следующей теоремой.

Теорема. Пусть выполняются условия У1-У4 . Тогда Vt е D₀₁ существуют решения уравнений (6), (7) и для них справедливы оценки

ReA(t)

\n(t,s)\< M₃exp —-—, t е (P q ) U D 01 U D 11 ;

lx(t,s)l < M7s,Vt е D01.

Справедливость теоремы установляется применением метода последовательных приближений к (6) и (7).

Последовательные приближения определяются так t

Пт=х0ехр —+ | f (т,Пт-1)е хр-^----— dT,

^{£                              8}

t0

n0(t,£) = 0,m = 1,2,....

t

A(t) — A(t)

Хт = I [b(T) + f(T, П + Хт-1) — f(r, П)]ехр-----------dr, t0

х₀(t, 8) = 0,m = 1, 2,....

• (8)    и (9) оцениваются Vt E D₀₁ , согласно выбранных путей интегрирования и доказывается их равномерная сходимость. Заметим, что линии уровня, определяемые гармоническими функциями, являются аналитическими кривыми и их уравнения можно представить параметрическими.

Пусть T1 = T1(s),T2 = T2(s),0 < s < s0 параметрическое уравнениелинии уровня (р0), а s-длина кривой (р0) от точки t0 до точки t = T1 + it2 ;  T1 = T1(a), t2 = T2(e), 0 < a < a0 параметрическое уравнение линии уровня (q) проходящая через точки t и т.

Сначала проведем оценку последовательных приближений (8).

Пусть t E (p₀\Vt E (р₀) (ReA(t) = 0) ^ |П 1 | < |х⁰|.

Из (8), учитывая У4 получим

|П 2 | < |х⁰| +М 2 J₀^S|n i ||T 1 ⁽s⁾ + it 2 ⁽s^)I ds <  |х⁰| + М 2 ¹х°¹ •M 0 S^(lT ‘ ⁽s⁾ + +it 2 ⁽s^)I < M o ),|П 2 |<|х^o|+M 2 M o |х^o|S.

Для выполнимости У4 положим |х⁰| + |х⁰|М₀М ₂s < М 1 .

Отсюда имеем

М 1 —|х⁰| ^S-|х^o|•M o M 2 .

Учитывая (10) получим

\П 2 \<М1.

Для П 3 имеем

S

S

\^П з \<\^х ° \ + ^М 2 ^М 0 \\H1\^ds< \^х ° \ + ^М 2 ^м /^(|х » | + I^х0! ^M ₀ ^M 2 ^s)ds<

s2

< \х⁰\+М ₂M₀|х⁰|S + (М ₂М 0 )² — = |х⁰|(1 + M₃s +

Пусть справедлива оценка

(М з §)² 2!

)•

где М2М0=М

Пт.\<   •" 1к '"3'.

Учитывая (11) из (8) получим

S т-1                    тт

\П т+1 \ <|х»|+M з \х«\\^^-ds< \х ° \ + Iх 0 |t⁽M^-= = t⁽Mг-

0 к=0                         к=0к=0

Справедливость оценки (11) доказана.

Оценку (11) можно заменить следующим

|nm| - |%0|е%рМзХ

При получении оценок для |Пт| мы формально предположим выполнимость условия

У3. Освободиться от этого формализма можно, положив

|х0|ехрМ3£ < М1 или

~    1    М1

^s - М₃ ^1п к°| .

Далее, не ограничивая общности, будем считать, что неравенство (10) выполняется для части (p₀) содержащегося в D₀₁ так как раздвигая границы D₀₁ можно обеспечить выполнимость (13). Таким образом все вышепроведенные операции законны и полученные оценки справедливы. Если учесть (13) то имеем

|Пт|-М1,т = 0,1,.

Теперь докажем равномерную сходимость (8) для t € (p₀). Учитывая У4 имеем

S

^|П 2

—

^П 1 ^|-М 2 ^М 0 /|П 1 |_Й5^-М з ^М 1 _?.

Далее

^|П 3

—

S s'2

П21 -Мзрщ —П1|с/5-М1Мз2-.

Продолжая процесс получим

,              ,         (М3£)

|Пт —Пт-1|-М1  3^-

(т — 1)

Из полученных оценок вытекает, равномерная сходимость последовательных приближений Vt £ (p₀) к некоторй функции П(t, е) , которая является решением (6). Если учесть (14), то для этого решения справедлива оценка

|П(t,E)|-М1,tG(po)                                    (15)

Пусть t € D^. Согласно выбранных путей интегрирования (6) представим в виде

S

.    ^(t(

П = x0exp-------+ I /(т, П)ехр

^(tGT)) — Л(т^))

Е

* (r1(s) + ir2(s))ds +

+J01W, П)ехр^^)^^))* (т‘(а) + ir2(a))da.

В (16) проведем преобразование

П =                           L П)ехр

^{E                      E}      0

X(t(

+ I /(т, П)ехр------------------ xx (t1(ct) + ir2(a))da, где t(s)

e (P0).

4(t⁽s)) — X(t(s))

E

xx (t1(s) + ir1(s))ds)j

E

В (17), выражение содержащееся в скобке [...], дает решение уравнения (6) при t(s) € (p₀) т. е. П(? (s), е). Согласно (15) для этого решения справедлива оценка

n(t(s),e) < M1,t⁽s⁾ e (p₀).

(17) можем переписать в виде

П = n(t(s), £)exp

A(t(J)) — A(t(s))

£

o'

+ / f(r,n)expA(t("))-Atl(g))

^x(t1(j) + ^^T2(j))dJ.

Для исследования уравнения (19) применим метод последовательных приближений. Последовательные приближения определим так

A(t(J)) — A(t(s)) Г              A(t(J)) — A(t(j))

Пт = n(t(s),£)exp 1   }---^--^+ | /(t, Пm-1)exp      J—-^ x

£             J£ x (t1(j) + ir2(j))dj.     n0(t, £) = 0, m = 1,2,...

Сначала оценим последовательные приближения (20), затем докажем их равномерную сходимость. Учитывая Re(t(s)) = 0 получим

|П1| < |n⁽t⁽s⁾,£^)|exp

Re A(t(J))

.

£

Далее

d

|nil<|nil+M2Mo/|nilexp

Re ( A(t⁽j)) — A(t⁽j)))   <

£

ReA(t(J))

< M1exp--------- + M₃M1exp

Re A(t(o))             Re A(t(o))

-------- J == M1exp--------

|П₂| < M1exp

Продолжив процесс получим

£

Re A(t(J))

----(I + M3J).

£

(1 + M3J),

Re A(t(J)) |Пт| < M1exp---------

m-1

V ^(M3^J^       ₉

> —n—,m = 1,2, .

k!

k=0

Из (22) Vm e Мимеем оценку

Re A(t(J)) |П_т| < M1exp----------expM₃J.

Если учесть, что D ограниченная область, то  exp M3 J < M₄.

Таким образом

ReA(t(J)) |Пт| < M₅exp-----------,

M₅ = M1M₄.

Теперь докажем сходимость последовательных приближений. Для этого оценим

^|Пт ^Пт-1|.

Имеем, учитывая У4 (за счет д, всегда можно добиться, чтобы (t, П_т) £ Н).

г      Re( A(t(d}} — A^o))

MIS М2Мо \ |П1| ^---------->ла <

Re A(t(d) < М3 Mi exp----д,

^|Пт—Пт-1^|< Miexp

Re A(t(d)) (M3д)т-1

,m = 1,2, .„

-      (m — 1)!

Таким образом, на основе полученных оценок можем утверждать, что ряд

2т=11Пт—Пт-11 сходится равномерно Vt £ D^ к некоторой функции П(t,E), которая является решением (19) для t £ D0_i.

Если учесть (23), то для этого решения справедлива оценка

|П| < M₅exp^(^,t £ D^.

Пусть t £ D0_i. Для этого случая, повторяя вычисления проведенные в 2 получим аналогичную оценку, оценке (24) т. е.

|П| < Msexp^f^kt £ D11.

Объединяя оценки (15), (24), (25) для П(t, е) можно записать оценку

ReA(t(a))

|П| < M₃exp----------S t £ ⁽po} U D$i U D1i.

Таким образом первая часть теоремы для П(t, е) , доказана.

Теперь докажем вторую часть теоремы. Как и в предыдущем случае оценим (9) и докажем их равномерную сходимость. Ограничимся только оценкой только первого приближения, а оценка для оставшихся приближений и доказательство сходимости повторяются вычисления проведенные в предыдущих случаях.

Пусть t £ (p₀) Тогда

S xi = ^ b^exp^^^-)^^^

S

(bi(x) = b(T)(Ti⁽s)) + i(T^⁽s))) = | bi(r)exp---( )  ^----(—dis.

К последнему интегралу, согласно У2, можно применить интегрирование по частям. Применяя этот метод, затем переходя к модулю, получим

^Ixi^I< M₆E,t £ (po)

t £ D0_i U D0_i. В этом случае, повторяя преобразование случая 2 (t £ D0_i), получим

S                       X        X                   X xi(t,-') = | b^T^exp---—— ----~“(Ti(s)) + i(T^(s))ds +

+ J b_i(t)exp^A^^ta^  Л^^) (т1(<г)) + i(r2(a))da =

= ехр^й^У^               + iftCs»] +

+ J^btfr) exp^^^^^r^a)) + i(r‘(a)) da (выражение содержащееся в скобке [...], есть функция

Xi(t, е) (t e (po))) =X1 (t(s), ejexp^^)^^) + + J /MYJexp^^—))—^—^^^    + i(r‘(a))da,

o

A(t(a)) — A(t(s)) x_i(t, e) = x_i(t, e) exp------------------- + £ ^

С         A(t(a)) — A(r(a)) ,     .

+ J bi(z)exp-----------------(т1⁽а)) +

⁰ +i(r2(a))da,. teD^UD^

В выражении (27)

|Xi(t,£)| < MiE,

A(t⁽a⁾) — A(t⁽s⁾) exp---------------

/?eA(t(T))   (   O(1),teDo\

|/| o^£iUDoOi.

Учитывая все сказанное, имеем

|xi(t,E)| < M₇E,t e D^iUDii,(M₆< M₆o)                             (28)

На основе (26), (28) можем написать оценку

|x₁⁽t,E^)|< M6oE,t e ⁽po) U D^ U D0i.

При оценке приближений x₁(t,e), (m = 2,3, .) достаточно рассмотреть случаи te ⁽po),t e D^i U D^i.