Расширенная характеристика динамического спектра нестационарного сигнала

Время-частотное и время-масштабное распределения (результат соответствующих преобразований) не дают полного представления об особенностях динамики анализируемого нестационарного сигнала. Для расширения характеристик такого сигнала использована квантово-механическая концепция (КМК) представления физических переменных в операторном виде. КМК в форме, адаптированной для области обработки сигналов, применена для получения текущих (мгновенных) значений вероятностных моментов первого– четвертого порядков, асимметрии и эксцесса частотного спектра нестационарного сигнала. Показана методология получения текущих характеристик, относящихся к текущим моментам реального времени эволюции сигнала.

ВВЕДЕНИЕ                      Текущие ("мгновенные") значения частоты и ширины полосы являются элементами важной

Представление о своеобразии и особенностях нестационарного сигнала (т. е. практически любого сигнала информационно-измерительной системы) дают характеристики структуры его частотного спектра. Для этого применяется одна из форм время-частотного преобразования или вейвлет-преобразования (ВП) [1-4].1) С помощью первых получают зависимость текущей частоты сигнала от времени, а с помощью второго (ВП) — зависимость масштаба от времени. Параметр масштаба ВП пропорционален обратной частоте. Поэтому оба преобразования фактически дают распределение частоты по времени, причем ВЧП — без преобразования аргументов, а ВП дает зависимость в плоскости время—масштаб, т. е. зависимость обратной частоты (в условных единицах) от вре-мени.2)

концепции в методологии анализа сигналов, которые используются при решении разнообразных прикладных задач в области связи, сейсмологии, системах мониторинга биологически значимых веществ в окружающей среде, непрерывного акустического и гидроакустического контроля. С точки зрения время-частотного анализа понятия мгновенных значений частоты и ширины полосы можно интерпретировать как условные статистические моменты первого и второго порядка, т. е. как спектральное среднее и среднеквадратичное отклонение, оцененные в предельно узком временнóм интервале сигнала. В соответствии с предлагаемой методологией, это — мгновенные текущие значения указанных характеристик спектра сигнала.

Использование двумерной плотности P ( t , ω ) (результата ВЧП, интерпретируемого как распределение вероятности сигнала на плоскости время—частота) позволяет определить условные спектральные моменты n -го порядка в виде соот-ношения³⁾

(«"), = P^ J ^P (, .^d^= шение ω = с/a (или a= с/ω), где a — параметр масштаба ВП, с — константа, определяющая выбор единиц для частоты ω (поскольку параметр масштаба имеет размерность времени).

j P ( t , o )d a

j G PP ( t , to )d to

Для сигнала, представленного в амплитуднофазовой форме s ( t ) = A ( t ) e^{J (} t ) , первый момент дается простым выражением : ( ^ _t = d ^ ( t )/d t = ^ '( t ), которое определяет текущую (мгновенную) частоту. Для такой же формы представления сигнала второй момент ^2²^ и дисперсия а ( t ), (которая характеризует текущий частотный диапазон сигнала в виде а_т ( t )) определяются соотношениями (2) и (3):

I + ( ^ '( t ) ) 2 ,

а ² ( t ) = ^ 2 ² ^ - ^) _t =

' A '( t ) ^

I A ( t ) ) "

Таким образом, текущие значения частоты и ширины полосы являются важными характеристиками свойств мгновенного спектра сигнала, меняющегося со временем.

Другая важная информация обеспечивается текущей величиной эксцесса.4) Для зависящей от времени спектральной плотности (распределения значений сигнала при достаточно "плотной" его дискретизации) моменты третьего и четвертого порядков, определяющие текущие значения асимметрии ("скошенности") и эксцесса, выражаются соотношениями (4) и (5). Строго говоря, эти статистические моменты являются условными, т. к. их получение связано с интегрированием по частоте (плотности) время-частотного распределения (ВЧР) (результата время-частотного преобразования (ВЧП) нестационарного сигнала)5):

^«(t ) = ttxJ( ® ^- И , ) P ⁽ t ^{, ю )d to ,} P ( t )             ^t

^M ' ⁴( t ) = P ( t ) j ( ^ ^- ^ tt ) 4 P ⁽ t ^{, Ю} )d ^ ^, где аналогично (1) P ( t ) = j P ( t, a )d ® .

Определение текущих значений моментов ВЧР по (4) и (5) вполне аналогично методу введения текущих значений моментов частоты в соотношении (1) с тем различием, что в нем использовалось маргинальное (условное) ВЧР при фиксированном времени.

Для получения статистических характеристик переменного во времени частотного спектра нестационарного сигнала более конструктивным и общим является метод, идея которого состоит в использовании операторного описания любой физической величины.6) В области обработки сигналов этот подход впервые применен Л. Коэном (L. Cohen) [16], [17].

Применение этого метода в области обработки сигналов в первую очередь связано с такими переменными как время, частота и параметр масштаба. Далее он будет использован для получения асимметрии и эксцесса как отражения текущих особенностей динамического спектра нестационарного сигнала. Предварительно метод рассмотрен в обобщенной форме с получением различных характеристик на основе использования квантовомеханической концепции (КМК), модифицированной Коэном применительно к анализу сигналов [18].

ОСНОВАНИЕ, ПРОЦЕДУРЫ И ОБЩАЯ ФОРМА МЕТОДА ПОЛУЧЕНИЯ ТЕКУЩИХ (МГНОВЕННЫХ) ЗНАЧЕНИЙ НЕКОТОРОЙ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ

Начальная разработка процедур КМК направлена на получение явных выражений для текущих значений статистического (более точно, вероятностного) среднего и дисперсии любой физической величины сигнала (например, частоты, масштаба). Отдельные процедуры, использующие операторный метод, появились в контексте время-час-тотного анализа сигнала в работах Вилле (Ville) [19] и Габора (Gabor) [20]. Затем процедуры расширены Коэном и использованы им для получения локальных вероятностных средних (математических ожиданий) физических величин сигнала с использованием операторного метода [21].

Основу метода и процедур составляет основная идея КМК, согласно которой можно получить среднее от количества а непосредственно из сиг- нала $(t), не выполняя предварительно некоторое "а-преобразование": S(a) = j$(t) • v*(a, t)dt, в котором v(a, t) — собственная функция, которая получается из соотношения A • v(a, t) = a • v(a, t). Так, средняя величина а и а2 (т. е. первые два общие момента) выражаются соотношениями (6) и (7):

( a² )_t = « a\ ) 2 ⁺ О ( t ) =

г A$ ( t ) J ² l $ ⁽ t ) ^ Re

Г A$ (t)J l $(t) Jim

A$ ( t ) $ ⁽ t )

aa^ = j a • | S ( a )| d a = j $ * ( t ) • As ( t )d t =

r As ( t ) I . .|2 .

= ^j ^-1 $ ⁽ t >1^d t ■

^a ²^ = j a ² • | S ( a )| d a = j $ * ( t ) • A ² $ ( t )d t =

В соответствии с таким подходом, частота го как физическая величина на основе КМК во временной области представляется оператором W =- i • | — | [20]. Для сигнала, представленного

l dt J в амплитудно-фазовой форме $(t) = A(t) • ei^(t), применение "частотного" оператора приводит к соотношению

=j

A^ • | $ ( t )|² d t ,

W • $ ( t ) = d ^ i d A /d t $ ( t )     d t A

где в последнем преобразовании в (7) использовано правило преобразования операторной алгебры, указывающее на существенную положительность второго момента ^ a ²^ (как это и должно быть). В выражениях (6) и (7) проведено интегрирование по времени, поэтому получено общее (глобальное) среднее ( a )и общий момент 2-го порядка ( a ²^, т. е. две текущие ("мгновенные") характеристики физической величины а .

В соответствии с КМК, величина A$ ( t )/ $ ( t ) разбивается на вещественную (Re) и мнимую часть (Im)

Из (12) непосредственно (как вещественная часть) получается обычное определение текущей (мгновенной) частоты динамического спектра нестационарного сигнала. Это — производная от фа

, х Г W • $(t))      dф . „ зы (2 = ----- = —. Мнимая часть опреде-

' ' t l $ (t) JRe dt                         P ляет квадрат текущей ширины полосы сигнала7)

^ ® ( t ) =

^Г W$ ⁽ t ) ^ ² = Г v $ ( t ) ^J, I x x у Im \

x 2

d A ( t )/d t ²

A ( t ) j

A$ ⁽ t ) =Г A$ ⁽ t ) ) ₊ i $ ⁽ t ) l $ ⁽ t ) j Re

г A$ ( t ) J

. $ ( t )

X ^{x 7} У Im

( i — мнимая единица), каждая из которых имеет определенное "физическое" значение. Это локализованные во времени (текущие) математические ожидания (т. е. вероятностные средние) двух характеристик динамического процесса или сигнала — носителя величины a ( t ). Средняя величина a на время t определяется реальной частью

к ^a\ =

г A$ ( t ) ^

l $ ⁽ t ) ^ Re

Ширина рассеяния a на время t (текущая дисперсия) определяется мнимой частью

° ²⁽ t ) =

г A$ (t) J l $(t) Jim

Текущее (на время t ) значение второго (нецентрального) момента ^ a ²^ определяется выражением

В общем виде текущее значение дисперсии выражается соотношением (14), отражающим дисперсию в виде центрального второго момента:

^ a ( t ) =

⁽ A - ( a \) • $ ⁽ t )

$ ⁽ t )

Использованная в (14) форма представления может служить для получения третьего и четвертого центральных моментов, т. е. моментов относительно текущего вероятностного среднего анализируемой характеристики динамического спектра.

ПРЕДСТАВЛЕНИЕ АСИММЕТРИИ И ЭКСЦЕССА КАК ТЕКУЩИХ ХАРАКТЕРИСТИК НЕСТАЦИОНАРНОГО СИГНАЛА

В статистическом смысле асимметрия и эксцесс определяются третьим и четвертым центральными

⁷⁾ В соответствии с соотношением (10), где роль оператора А заменяет W . Метод, основанный на КМК, дает положительное значение дисперсии частоты о^-2 ( t ), а (Т_ю ( t ) интерпретируется как текущий частотный диапазон сигнала.

моментами распределения анализируемой случайной (стохастической) переменной. Для определения текущих ("мгновенных" значений) асимметрии и эксцесса динамического спектра сигнала использована КМК в интерпретации Коэна. По аналогии с первым моментом, представленным выражениями (6) и (8), третий момент определяется соотношением

^ a ³ ^ = J s * ( t ) • A ³ s ( t )d t =

=J

' A ³ s ( t ) ^

v ^{s (} t ) L

' A3 s (t) I vs (t) L

• ^{s (} t fd t =

и четвертым моментами ( У ( t ) и У ( t )) динамического частотного распределения сигнала, получаются заменой A на A - ОУ, в выражениях (19) и (20). При этом (аналогично асимметрии и эксцессу, определяемым для обычной плотности распределения вероятности) текущие асимметрия и эксцесс сигнала представляются соответственно как отношения третьего и четвертого центральных моментов к текущему второму центральному моменту. С помощью операторной процедуры КМК, текущие (мгновенные значения) асимметрии ( у ) и эксцесса ( к ) выражаются соотношениями:

' A ³ s ( t ) I v ^{s (} t ) J

• | s ( t )|² d t .

Y a ( t ) =

УЖ = ^л t )

Re

Таким же методом по аналогии со вторым моментом из (7) и (11) получается соотношение для четвертого момента:

= ( A и ГЬ ш

^{s (} t )

j Re

( ^{A -} Ж ) • ^{s (} t ) ^{s (} t )

^ a ⁴ ^ = J s * ( t ) • A⁴ s ( t )d t =

^K a ⁽ t ) =

=J

' A ² s ( t ) v ^{s (} t )

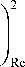
A ² s ( t ) |

. s ( t )

x v 7 / Im

• I ^{s (} t )l^{2 d} t =

у М = ж t )

=J

A ² s ( t ) ^{s (} t )

• I ^{s (} t )l² d t .

Как и в случае первых двух моментов, обсуждавшемся выше, под интегралом стоят текущие (локальные по времени) моменты. Поэтому непосредственное выражение текущих моментов третьего и четвертого порядков определяется соотношениями:

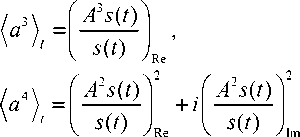
A ² s ( t ) ^{s (} t )

Кроме того, как и первые два момента, нецентральные моменты удовлетворяют необходимому условию: их временное усреднение дает средневзвешенные ("глобальные") моменты (для интервала времени, использованного для усреднения):

а а 3^ = J а3 S ' ( а ) 2 d a = J а а 4 = J а4 S ( а ) 2 d а = J Текущие характерисг цесс, — определяемы	f A 3 s ( t ) V s ( t ) A 2 s ( t )	) • | s ( t )2d t ,     (19) J Re 2 • s ( t ) 2 d t .       (20) - асимметрия и экс-ральными третьим
	s ( t ) тики — е цен

( A - H t ) ^{2 s (} t ) ^{s (} t )

(A - и)•s(t)

^{s (} t )

^{s (} t ) ( A — n t ) ^{2 s (} t ) | ( A — <4) • ^{s (} t ⁾⁴

Текущая асимметрия для "мгновенных" распределений частоты и масштаба нестационарного сигнала

Использование в процедурах анализа (расширенных характеристик нестационарного сигнала) модели операторного метода КМК позволяет получить текущую асимметрию мгновенных распределений частоты и масштаба.

Для сигнала в форме s ( t ) = A ( t )e ^{iф (} t ) третий центральный момент частоты (оператор которой W= = -i (d / d t )) определяется соотношением⁸ )

( W - d ^ d t ) ³ s ( t )    .A "'( t )

-------------------------= i .

^{s (} t )              ^{A (} t )

⁸⁾ Для получения центрального момента в (23) из оператора частоты W вычитается его текущее среднее (первый момент) частоты, равный d ф /d t (согласно формуле (12) и следующей за ней формуле в тексте). A "' — принятое обозначение производной третьего порядка (вместо d³ A /d t ³).

Поскольку значение этого оператора чисто мнимое, то, как в (9), текущее значение третьего центрального момента частоты (выражающееся вещественной частью оператора) равно нулю. Отсюда следует, что асимметрия частотного распределения (мгновенного частного спектра сигнала) равна нулю.9)

Таким же образом (как в случае асимметрии) для масштаба [10], [13], оператором которого является C = (1/2) • ( TW + WT ) , в соответствии с (19), асимметрия (виртуального распределения) текущего масштаба равна нулю.

С с2 )t = t2 (ф'( t))2 +

Г A '( t ) 1 1 t— — + - ,

V A ( t ) 2 ^J ’

^T -( t ) = ¹

Г A( t ) + 2 1 • A '( t ) 1

V       A ( t )       J ’

_t = t ² ( ф '⁽ t ) ) ² -

A "( t ) A ( t )

„ A '( t )   1

2 1——--

A ( t )   4

+

+ 4 t ²

Текущее значение эксцесса мгновенного (текущего) спектрального распределения нестационарного сигнала

Если принять A = W и ^ t = d ф /d t в соотношении (22) и использовать амплитудно-фазовую форму представления сигнала в виде s ( t ) = A ( t )e ^{iф (} t ) , то текущее значение эксцесса мгновенного спектра сигнала выражается формулой

/                         X          \2

( AXA 1       1         1

ф '( t ) + - ф "( t ) I + t ф '( t ) , (29)

V A ⁽ t )        ² J j

УД t ) =

( A ( t ) ) • A "( t ) ( A X t ) ) 4

Четвертый нецентральный и четвертый центральный текущие моменты частоты определяются выражениями:

⁴    ₌ Г A "( t ) )                              /₂₅)

t ) ( A ( t ) J ’                              ⁽²⁵⁾

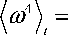
( ф '⁽ t ) ) 2 ^-

A "( t ) Y ₊

A ( t ) ^J

( AXA ²

+ ф "( t ) + 2 ф '( t ) I . v           A ⁽ t )        J

Текущее значение эксцесса мгновенного (текущего) масштаба сигнала

Использование оператора С , представляющего масштаб сигнала (вместо действующего оператора А ), и соответствующая модификация соотношений (14), (18) и (22) позволяют получить текущие значения моментов второго и четвертого порядка для масштаба ( с ):

⁹⁾ Этот результат может рассматриваться как обобщение глобальной асимметрии спектра сигнала s ( t ) = = A ( t ) c ™ ’ t . Асимметрия такого сигнала равна нулю, т. к. спектр симметричен относительно частоты го ₀. Аналогично нулевая текущая (мгновенная) асимметрия получается, если текущий спектр симметричен относительно текущей частоты ф' .

^ c⁽ t ) = 116

Г A ( t ) + 8 1 • A '( t ) + 4 1² A "( t )

V              A ( t )

В соответствии с этим, текущее (мгновенное) значение эксцесса (виртуального текущего распределения) параметра масштаба сигнала определяется соотношением

^К с ⁽ t ) =

( A ² ( t ) + 8 tA ( t ) A '( t ) + 4 1 ² A ( t ) A "( t ) ) ² ( A ( t ) + 2 tA '( t ) ) ⁴

Локальный эксцесс

О вероятностной характеристике параметра а нестационарного сигнала можно говорить, как о локальной, в том случае, если она определена на основе (условного) распределения этого параметра на множестве, где некоторый другой динамический параметр b имеет фиксированное значение. Рассматривая затем (после получения соотношения, определяющего локальную характеристику для а ) зависимость локальной характеристики а от значений параметра b , можно получить дополнительное представление о динамике частотного спектра, которое отражает совместное изменение особенностей распределения параметра а , обусловленных меняющимся (возможно, более медленно) параметром b . Концепция локальной характеристики параметра а сигнала при фиксированном значении b дуальна: может рассматриваться локальная вероятностная характеристика параметра b сигнала при фиксированном значении а, а затем и зависимость этой локальной характеристики b от возможного изменения а .

Результаты (27)-(31) можно расширить, рассматривая два произвольных параметра сигнала в качестве переменных а и b с соответствующими операторами A и B и преобразованиями сигнала S ( а ) и S ( b ). Использование прежних процедур ведет к соотношениям:

^ 2 ( ь ) =

( A - ^b) ) ^s ( b )

S ( b )

^ 2 ( ь) =

( A — ^bb ) 2 ^s ( ^b )

S ( b )

Следствием двух формул (32) служит соотношение (33), определяющее величину локального эксцесса для динамического параметра а при заданном значении величины другого параметра b ¹⁰⁾:

^K a ⁽ b ) =

д 2( ь ) = ^ 4 ( ь )

^ ( b ) ( A - ^b_b ) ² ^ ( b ) 2 | ( A - W b ) s ( ^b )f

ЗАКЛЮЧЕНИЕ

Для получения спектрально-временнóго представления нестационарного сигнала используется несколько видов время-частотных и вейвлет-преобразований (ВЧП и ВП). Результатом таких преобразований являются (соответственно) время-частотное и время-масштабное распределения. Помимо этих хорошо исследованных методов целесообразно иметь характеристики частотной структуры и ее динамики в реальном времени эволюции сигнала. Кроме того, желательно, чтобы эти характеристики в определенной степени отражали понятия статистического анализа. В связи с этим введено понятие текущих ("мгновенных") значений различных параметров, отражающих особенности изменения структуры сигнала (и следовательно, порождающего его процесса). В основу получения расширенных характеристик нестационарного сигнала положена квантово-механическая концепция (КМК) представления основных физических переменных в форме операторов. Адаптация КМК для области обработки и анализа сигналов выполнялась в работах Вилле, Габора и Коэна.11) Проведенное обобщение методов КМК позволило создать систему метрологических показателей ВЧП и ВП и наметить методологию получения ряда мгновенных (текущих) характеристик, более полно отражающих особенности динамики нестационарного сигнала и способствующих углубленной интерпретации измерительных данных.

― Получены аналитические выражения текущей величины вероятностных моментов первого– четвертого порядков для любого динамического параметра нестационарного сигнала. Они представлены в форме условного среднего с использованием время-частотного распределения с помощью а-преобразования на основе собственной функции оператора А (представляющего параметр а) и в форме представления оператором (А) и анализируемым сигналом.

― Представлены значения текущих (мгновенных) моментов (в том числе центральных) для частоты, частотного диапазона, масштаба, асимметрии и эксцесса виртуального спектрального распределения нестационарного сигнала.

― Показана модификация операторного представления любых двух параметров сигнала, позволяющая получать "локальную" вероятностную характеристику одного из параметров при заданном (выбранном) фиксированном значении второго параметра сигнала. В качестве локальной может выступать любой из этих двух параметров, т. е. свойство локальности дуально относительно каждого из них.