Расширенная межотраслевая модель региона на основе методики Миядзавы

Важнейшим инструментарием структурного анализа и моделирования межотраслевых связей в национальной экономике является межотраслевая модель, формируемая на основе таблиц «затраты — выпуск» [5, 6, 7, 10]. В той или иной степени внимание российских исследователей уделяется возможностям применения модели «затраты-выпуск» в региональном анализе [1, 2, 8]. В 2013 г. по экономике Бурятии были разработаны базовые таблицы «затраты — выпуск» за 2011 г. по 50 видам экономической деятельности, которые в целях структурного анализа и сценарных расчетов были также агрегированы до 16 отраслей. На основе агрегированного межотраслевого баланса были проведены сценарные расчеты развития экономики Бурятия [4] с использованием линейной статической межотраслевой модели региона:

,

где:

— вектор валовых выпусков, — вектор конечного потребления (конечного спроса) в регионе (II квадрант), ;

— квадратная матрица промежуточного по требления (I квадрант), где коэффициент , представляющий собой затраты продукции (услуги) вида I на единицу продукции (услуги) вида j, является элементом технологической матрицы прямых затрат .

В данной модели экзогенными величинами являются как коэффициенты прямых затрат, так и вектор конечного потребления (конечного спроса). При этом вектор конечного спроса, как известно, включает в себя несколько важных компонентов (потребление домашних хозяйств, государственные закупки, элементы валового накопления, показатели ввозимых в регион и вывозимых из региона товаров), каждый из которых зависит от множества различных факторов. В этом смысле более углубленному системному анализу прямых и обратных связей региональной экономической системы способствует увеличение доли эндогенных переменных вплоть до перехода к моделям в динамической постановке [3].

Данному направлению отвечает межотраслевая расширенная модель региона, базирующаяся на методической работе японского исследователя Миядзавы по эндогенизации домашних хозяйств в модели «затраты — выпуск» [11, 12]. В матричной модели Миядзавы для анализа взаимосвязей между различными группами доходов в процессе их формирования разработан многосекторный множитель, который, в отличие от «межотраслевой матрицы мультипликаторов» Леонтьева [6], формируется путем включения процесса генерации дохода. Соответственно в модели Миядзавы генерируются различные мультипликативные матрицы. Миядзава делает важный вывод: величины дохода различаются в зависимости от пропорции автономного спроса.

Во втором квадранте межотраслевой модели (таблицы «затраты — выпуск») вектор конечного спроса разбивается на две составляющие:

, где                — вектор-столбец потребления продуктов (услуг) все ми домашними хозяйствами;

Г = О1.....— вектор-столбец автономного конечного спроса

(без потребления домашних хозяйств), включающий валовое накопление основного и оборотного капитала, государственные закупки, а также сальдо вывоза-ввоза товаров.

Каждый элемент вектора равен:

, где ^ir — потребление i-го продукта (услуги) r-й доходной группой домашних хозяйств (i = l,...,n; т = l,...,q), или элемент матрицы потребления домашних хозяйств ^(nxq) — №r), имеющей вид:

/du ■■■ d_1\ d =     ;               ; .

\ ^nl """  ^nq /

Учитывая, что потребление домашних хозяйств финансируется за счет получаемых доходов, по каждому виду домашних хозяйств функциональное потребление какой-либо продукции (услуги) можно представить как:

d = Г ■ 7

^ir^r, где ^ir — удельное потребление i-го продукта (услуги) в расчете на 1 денежную единицу (напр., 1 руб., $1 и т.п.) дохода домашних хозяйств r-й доходной группы (i = 1, — ,71; r = 1, ...,q), или элемент матрицы удельного потребления домашних хозяйств ^(nxq") (cir):

;

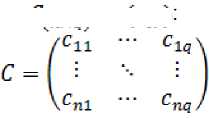
2y — общие доходы каждой r -ой

доходной группы домохозяйств

q) , или элемент вектора-столбца доходных групп домашних хо- зяйств:

z = (z^...^)^{1 .}

Тогда вектор-столбец конечного спроса во втором квадранте равен:

y = Cz+f . (1).

Соответственно для первого и второго квадрантов модели соотноше- ния являются следующими:

x = Ax + у = Ax + (Cz + /) .

Вернемся к матрице потребления домашних хозяйств D(nxq} — (^ir) . Просуммируем элементы данной матрицы по каждому r -му столбцу, получив тем самым для каждой r -ой группы домашних хозяйств общие расходы на потребление всех благ:

d =У^п d =У^п c z = z У^п c = 1

“-r Zj[=i “ir Zji=i ^cir^z,r ^r Zj[=i ^cir > V             ^.

Обозначим через b_r=^₌₁c_ir, (r = l,...,q), где b_r — удельное потребление для r -ой группы домашних хозяйств всех продуктов (услуг) в расчете на 1 денежную единицу (1 руб., $1 и т.п.) общего дохода 2^ (r= l,...,q).

Тогда dT = brzr, (r = 1,..., q)

Вообще говоря, показатель d.y есть часть располагаемого дохода по каждой группе домашних хозяйств, который равен разности между общим доходом 2y и всеми уплачиваемыми налогами. Располагаемый доход, в свою очередь, распределяется на сбережения домашних хозяйств и потребление.

Обозначим для каждой r -й группы домашних хозяйств: t_r — расчетная налоговая ставка, Sy — удельное сбережение (норма сбережения). Тогда для каждой r -й группы домашних хозяйств располагаемый доход равен:

а располагаемый доход, расходуемый на потребление всех конечных благ, равен:

Таким образом, естественным ограничением для удельного потребления всех конечных благ по каждой r -й группе домашних хозяйств являются значения налоговых ставок и нормы сбережений, т. е.:

q) ^.

;”=1cir = (i-tr)(i-sr)

Определим структуру потребления благ по каждой r -ой группе домашних хозяйств:

,

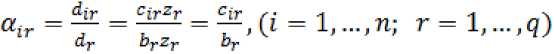
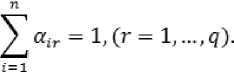
Таким образом, зная по каждой r -й группе домашних хозяйств исходные информационные данные по структуре потребления благ, а также расчетные значения налоговых ставок и норм сбережений, можно определить матрицу удельного потребления домашних хозяйств:

,

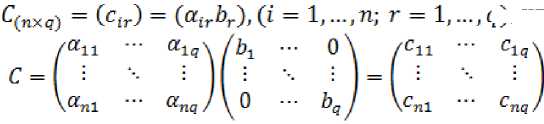
q) , или

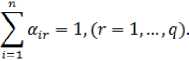
Раскроем зависимость доходов домашних хозяйств от объемов выпускаемых в регионе продуктов (услуг). Общий доход каждой группы домашних хозяйств есть часть валовой добавленной стоимости, функционально связанной с объемами выпускаемых продуктов (услуг). Представим каждый элемент вектора доходных групп в виде:

z_r = LpiZ_ri = S”=i ^гЛ , (r = 1,.... q) ^,

где Zrj — доходы, выплачиваемые r-й группе домашних хозяйств, участвующих в выпуске продукции (услуги) j-го вида экономической деятельно- сти; ^rj — доходы, выплачиваемые r-й группе домашних хозяйств в расчете на единицу стоимости валового выпуска продукции (услуги) j-го вида экономической деятельности, т. е.vTj = (r = ^-л;; = i,- -,™). Соответствующая прямоугольная матрица доходов ^(qxn) - (Zrj), имеет вид:

а вектор-столбец доходных групп домашних хозяйств по всем видам экономической деятельности равен:

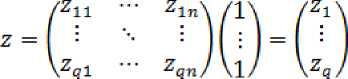
Обобщая выражение (2) для всех групп домашних хозяйств, получим в векторно-матричном виде следующее выражение:

/Zl\ /yll Vln\ /Xl\ г = I : J I :             : j | j - Fx ,                              (3).

\ I \ 77 • • ■ 77 / \ / X^q/ X^ql ^qn/ X^n/

Где         V(_qXn) = (v_rj\(r = l,...,q; j = 1, ...,n).

Подставим выражение (3) в выражение (1) и получим:

у = CVx + /.

Произведение двух прямоугольных матриц C и V дает квадратную матрицу               :

/cii  - CiaX/Vn  •••  vln\   /cM  ... cln\

C = CV =   :     •••    : H =   = : X : .

\L„i        L_nq/        "    ^qn/    \C_ni       C_n71/

Вектор потребления продуктов (услуг) в конечном счете определяется

Соответственно для первого-второго квадрантов модели имеем сле-

дующие соотношения:

x = Ax + у = Ax + d + f = Ax + CVx + f = (Л + C)x + f (4).

Матрицы A иC – квадратные, имеют одинаковую размерность (И X 7l) .

Матрица c , будучи результатом перемножения двух прямоугольных матриц (как правило, n >  q ) — вырожденная, ее определитель равен нулю (строки ее линейно зависимые). Ее экономический смысл: каждый из ее

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА.

элементов есть удельное потребление i -го продукта (услуги) в расчете на 1 денежную единицу (1 р., $1 и т. п.) стоимости валового выпуска продукции (услуги) j -го вида экономической деятельности (i,j = l,...,n).

Если матрица A не является вырожденной, то результатом суммирования двух матриц A иC также будет невырожденная матрица, а значит, будут получены неотрицательные значения валовых выпусков при данных (задаваемых) значениях экзогенных параметров вектора /.

Преобразовав выражение (4), получим систему линейных уравнений:

,

решаемую любым известным алгебраическим способом относительно вектора X при задаваемых экзогенно значениях вектора / . Здесь Е(пхп) — единичная матрица.

Как и в модели Леонтьева, используя метод обратной матрицы, получаем матричный мультипликатор:

В = (E - A -CV)"1

,

имеющий самостоятельное экономическое значение (полные затраты как сумма прямых и косвенных затрат различных циклов).

В результате определяем вектор валовых выпусков:

• х = (Е — A —CVy^xf = Bf

и строим таблицу «затраты ‒ выпуск»:

Ax + (CKx + f) = Ax + (Cz + f) = Ax + y = x с отражением показателей первого квадранта (матрица промежуточного потребления), второго квадранта (по видам конечного потребления с подробным отражением потребления домашних хозяйств) и третьего квадранта (с выделением групп доходов домашних хозяйств).