Расстановка корпусов плуга

В настоящее время в Западной Сибири, в том числе в Омской области, все большее распространение получают технологии обработки почвы без оборота пласта даже в зонах, не подверженных ветровой эрозии.

Но при ежегодной безотвальной вспашке появляются проблемы. Верхний слой почвы обесструктуривается, становится пылевидным, насыщается семенами сорняков, а вся технология требует применения гербицидов, которые отрицательно влияют на экологию. Нижние слои пахотного горизонта год от года уплотняются движителями энергонасыщенных тракторов (особенно колесных) настолько, что почвообрабаты-

вающие орудия сами под действием собственной силы тяжести не заглубляются. Для устранения этих недостатков рекомендуется раз в три или четыре года пахать отвальным плугом, чтобы обернуть пласт обесструктуренным, насыщенным сорняками слоем почвы вниз, откуда сорняки не прорастут или прорастут ослабленными [1].

Для свободного прохода почвенного пласта между корпусами их необходимо расставить так, чтобы предыдущий корпус был вне зоны деформации почвы следующим корпусом. Таким образом, межкорпусное расстояние (по ходу плуга) складывается из габарита корпуса по длине и величины зоны деформации. От межкорпусного расстояния зависит длина плуга и устойчивость его хода по глубине обработки и ширине захвата (качество вспашки), а также маневренность всего пахотного агрегата [2].

Целью работы является повышение качества вспашки при снижении металлоемкости плуга.

Объекты и методы

Определению зоны деформации двугранного клина посвящен целый ряд работ. Показателем величины деформации является угол скалывания у - угол между плоскостью скалывания и направлением движения лезвия клина.

Основоположник земледельческой механики В.П. Горячкин [3], используя теорию Мора, получил:

^ = 90 0 - ^а + ^ф + ^М , (1) где а - угол постановки клина к дну борозды; ф - угол трения почвы о сталь; д - угол внутреннего трения почвы.

Но эта формула точна для α = 9°, а при α = 30° дает расхождение с опытными данными. Объясняется это изменением коэффициента трения почвы о сталь при изменении угла постановки клина к дну борозды [4].

На основании теоретических и экспериментальных исследований П.Г. Свечников [5] получил следующую зависимость:

tg V = cos а . (2)

По аналогии с двугранным клином угол скалывания у должен измеряться в плоскости, перпендикулярной плоскости трехгранного клина АВС (рис. 1), в которой лежит равнодействующая силы нормального давления N и силы трения F [4] . Сила трения F действует по траектории движения пласта S . Значит, равнодействующая сил S и F будет лежать в плоскости, образуемой векторами S N . Положение вектора S в плоскости клина АВС определяется следующим уравнением [6]:

tg n = cos s • ід ү . (3)

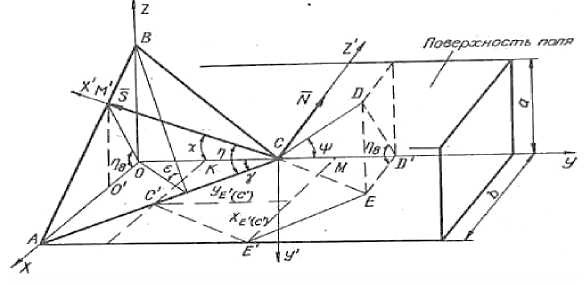
Рис. 1 . Расчетная схема для определения зоны деформации почвы трехгранным клином

Для дальнейших рассуждений определим положение плоскости S N по отношению к осям X, У, Z. Построим новую систему координат так, что ось X пойдет по S, ось Z' по N, а ось У перпендикулярно этим осям, т.е. плоскости S N . Определим направляющие косинусы осей X', У, Z' в системе координат X, У, Z. Направляющие коси- нусы осей X' и Z, направленных соответственно по векторам S и N, известны [6]. Для определения направляющих косинусов оси У (12; т2; п2) составим следующую схему:

X

X

cos η sin γ – cos ε cos γ sin η

l 1

У

ctg⁸. УУ -----Г" \ Ctg 8 + cos ү

Z

l 2 sin ε cos γ

l 3

У -cos п cos ү - cos е sin ү sin n

m 1

m 2 sin γ sin ε

m 3

Z sin ε sin η

n 1

^{- COS}YJ —2---- y

У Ctg 8 + COS ү

n 2

cos ε

n 3

Значения 1 2 , m 2 , n 2 , определим из следующей системы уравнений:

l₃l ₂ + m₃m ₂ + n₃n₃ — 0;

• < ll + m_xm ₂ + nn — 0;

  
  

2  22

l₃ + m ₂ + n₂ — 1.

Подставим известные значения из схемы в уравнения системы (4), проведем преобразования и найдем значения 1 2 , m 2 , n ₂ .

Комбинацию знаков n ₂ и 1 2 возьмем по направлению осей на рис. 1. Найденные значения m 2 , 1 2 , п ₂ запишем в схему и проанализируем ее.

Равенство нулю направляющего косинуса между осями У и У является условием их перпендикулярности. Но ось У перпендикулярна и плоскости S N. Значит, ось У лежит в плоскости S N . Отсюда следует, что:

• -    траектория движения пласта S есть линия пересечения плоскости клина АВС с перпендикулярной ей плоскостью, проходящей через ось У.

• -    угол резания х [6] лежит в плоскости, перпендикулярной плоскости клина АВС.

Тогда угол скалывания у, лежащий в плоскости S N, будет так же, как и угол резания х, измеряться от оси У, т.е. угол резания х и угол скалывания у лежат в одной плоскости, перпендикулярной плоскости клина АВС. Это дает право предполагать, что зависимость (2), полученная для двугранного клина, может быть применима и для трехгранного в следующем виде:

tgy = cosx .                                                                            (5)

Угол х может быть определен по известной зависимости [6]:

sin x = sin ү sin е.                                                                       (6)

Для определения величины зоны деформации нужно определить координаты точки D - точки выхода плоскости скалывания на поверхность (рис. 1).

Удобнее координаты точки D отсчитывать от носка клина (точка C).

X d ( C ) —

a tgne ’

V

D ( C )

a sin iygy

Прямая ЕЕ' (рис. 1) является горизонтальной проекцией линии пересечения плоскости скалывания с поверхностью поля при блокированном резании. Она параллельна лезвию клина на всех участках по ширине захвата, где а = const . Точка E ' - горизонтальная проекция точки пересечения этой линии с верхним ребром пласта. Это точка возможного контакта скалываемой части со стойкой (башмаком) предыдущего корпуса.

Для экспериментальной проверки полученных зависимостей были изготовлены трехгранные клинья с различным сочетанием углов γ = 30–60° и ε = 25–65°, одинаковой ширины b = 35 мм и высоты, равной 35 мм. Глубина хода лезвия клина во всех опытах 25 мм. Деформируемая среда - песок сухой просеянный и песок влажностью 16%.

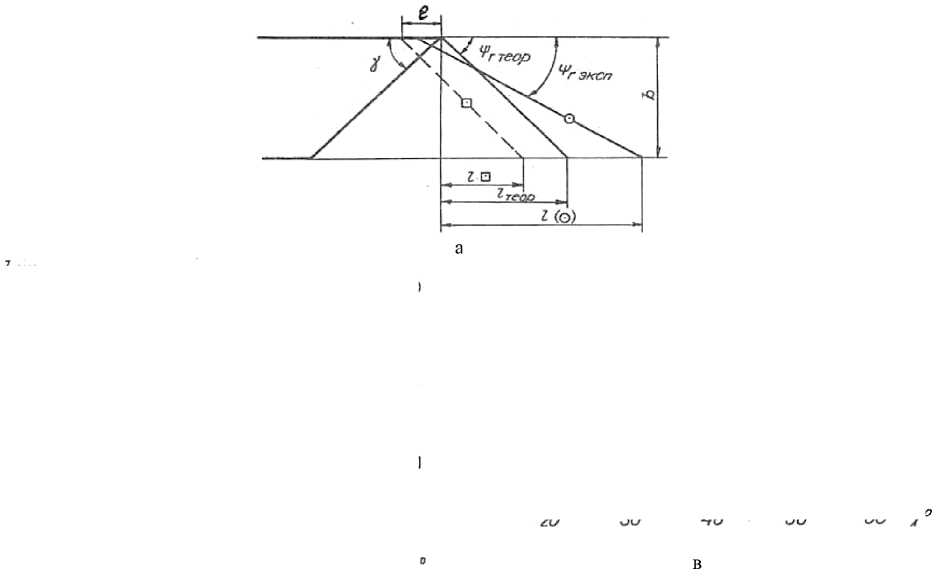
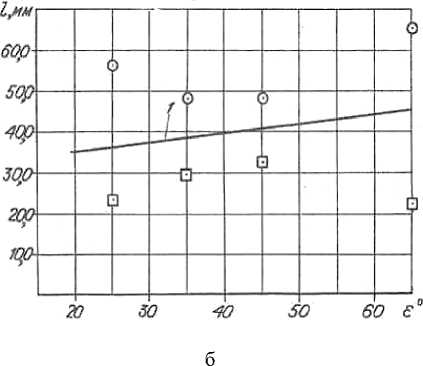
Рис. 2. Зона деформации трехгранным клином при полусвободном резании: а - схема деформации;

б - теоретическая зависимость 1 ( l = f(e) при b = 35 мм, а = 25 мм, ү = 45°);

в - теоретическая зависимость 2 ( l = f(Y) при b = 35 мм, а = 25 мм , е = 25°);

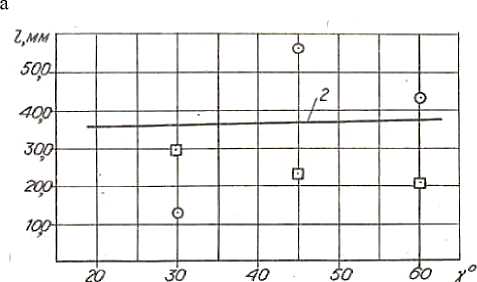
О И экспериментальные данные соответственно для сухого и влажного песка v ,     экспериментальные данные соответственно для сухого и влажного песка

• В.П. Горячкин [3] указывал, что теоретически должен быть намечен двоякий путь при рассмотрении резания в неограниченной (блокированное резание - в условиях первой борозды) и ограниченной среде (например, полусвободное резание).

Наличие свободной борозды с одной стороны деформируемого пласта приводит к более легкому смещению его в эту сторону. Поэтому действие угла резания трехгранного клина проявляется главным образом в направлении открытой борозды, т.е. в горизонтальной плоскости. Величина деформации при этом характеризуется горизонтальным углом скалывания ^ _г (рис. 2). Для определения расчетным путем угла ^_г можно воспользоваться уже известной зависимостью (2):

tg y _r = cos х .                                                                    (9)

Результаты исследований

Для определения величины деформации в линейных единицах определим l – расстояние от носка клина до точки выхода трещины к стенке борозды (рис. 2).

l = —— = - b- .                                               (10)

tg^_r  cos x

На основании этой формулы построим теоретические зависимости l = f ( γ ) и l = f ( ε ) при b = 35 мм и сравним их с экспериментальными данными (рис. 2).

Для определения экспериментальной величины зоны деформации при полусвободном резании замерялся угол между направлением движения и трещиной (уГзксп) и фиксировалось также положение вершины этого угла относительно носка клина е (рис. 2). Экспериментальная величина деформации в линейных единицах может быть определена по следующей зависимости:

l = —ь—

эксп tgV Гжсп

При полусвободном резании величина зоны деформации зависит от обоих углов ( γ и ε ), но при малых ( ε ) (примерно равных углам у существующих рабочих органов) угол ( γ ) мало влияет на величину зоны деформации.

Заключение

Сравнивая теоретические и экспериментальные данные (рис. 2), можно сделать вывод, что зависимость (10) дает усредненное значение между величинами деформации, полученными экспериментально для разных по свойствам сред. Сыпучая бессвязная среда была представлена воздушно-сухим песком. Второй почвенной средой был песок, доведенный до влажности, при которой он поддается формовке, то есть в какой-то степени приближается к свойствам «спелой» почвы. При проектировании плугов общего назначения предполагается их работа на разных по типу и влажности почвах. Поэтому для определения зоны деформации, необходимой для расстановки корпусов этих плугов, можно применить зависимость (10).

P.V. Chupin, A.Yu. Golovin, E.V. Demchuk, A.S. SoyunovOmsk State Agrarian University named after P.A. Stolypin, Omsk

Arrangement of plough bottoms