Расстояние от точки до конуса в гильбертовом пространстве

сЗ — Ж1

Учитывая, что получаем

d(x, K(ei,a)) =

Vi+>

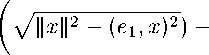
41=1.^).

Расстояние достигается на векторе

(У||ж||² - (е^+^х^ИРУИ² ~^У² - (ei, _Ж))

U                (1 +^2)^1^112 _(еьж)2

Наконец, если х ^ K(ei, а) и ж Е — K(ei, \/1 — а²), то ж Е — К* (ei, а) и ж = 0 + ж, проекция ж на К^е^,^ есть 0, a d(x, К^е^, а)) = ||ж||. Итак, получаем следующую формулу:

0,

d^x, К^ву, а))

если ж Е К(^ei, а);

если ж ^ A"(ei,а) и ж Е — К^е^, V1 — а²);

если ж ^ К(в1,а) и ж ^ —К^е^, \/1 — а²).

ЗАМЕЧАНИЕ. При a = ^ получаем формулу (4) из примера 2.1.2 в [4].

2°. Рассмотрим теперь произвольный круглый конус К^а,^, где a Е Н — произвольный вектор, ||а|| = 1 и а Е (0,1). Пусть П_ш — преобразование Хаусхолдера [5], переводящее вектор а в вектор ei.

Тогда П_ш : Н —» Н, w = a — ei, П_ш — унитарный оператор, т. е. Uj¹ = U* = И_ш. Согласно утверждению 1.5.2 И_ш переводит конус К^а,^ в конус K^e^^aY

Пусть ж Е Н — произвольный вектор. Имеем СТДо) = ei, и_ш^е^ = а,

иш^ = ж +

Ж1 — (о,ж)

1—01

а —

Ж1 — (о,ж) 1—01

Так как Пш — изометрия, то d^x,K^a,«Y = d(UY(xYK(e[,a)Y

Если ж Е К (а, а), то d^x, К Уд а)) = 0. Если ж ^ К (а, а) и ж Е — К (a, V1 — а²), то (7_ш(ж) ^ КУ^а) и ж Е —K(ei, V1 — а²) и, значит, в этом случае

d(x,K(a,a)) = ||П_ш(ж)|| = ||ж||.

Если же ж     К (а, а) и ж —К^а, V1 — а²), то и_ш^ ^ К (ei, а) и и_ш^ ^

-К^е_ъУТ^^ следовательно, в силу предыдущего пункта, имеем

„           У . ж_х-(о,ж) ж_х-(о,ж)         Д

о(ж,А(о,а)) =d ж 4---------а---------ei,A(ei,a) = у 1 — (2-1            1 — С1у                  у

^^-    ((2-) ж)) ((2-1    1)           Л Т, ч

= ot\ ||ж|| — (е1,ж) Н--— у 1 — а^уа^х) =

V L                   1 — 01 J

= а у/ ||ж||² — (о, ж)² — У1 — а² (о, ж).

Найдем проекцию вектора ж на конус К^сусф. Имеем d^x,K^a,a^ = d^U^^x), К(в[, а)), т. е. проекция ж на Кфа,сф равна образу проекции вектора жх — (а, ж) Ж1 — (а, ж)

и^дх) = ж 4------- —а -------—61 1 — (2-1              1 — (2-1

на К^е^оф при отображении П_ш. Согласно предыдущему пункту, получим

(FRF^F^F + («, ж) ^=) (^= VFF^Ta?^ - («, ж))

V1№HXFP +"7^(а,ж)      Ж1-(а,ж) Ж1 - (а,ж) х

(V1 — а2-у/||ж||2 — (а, ж)2 + а(а, ж))(а-^/||ж||2 — (а, ж)2 — V1 — а2(а, ж))

VINI2 - (а,ж)2

(1 — а2)-\/||ж||2 — (а, ж)2 + а\/1 — а2(а, ж)

VFII2 - (а,ж)2

Итак, получаем следующую формулу:

°,

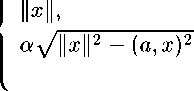
если ж Е К (а, а);

если ж ф К (а, а) и ж Е —К (a, V1 — а²);

М^ф,^ = < g Е С^д]

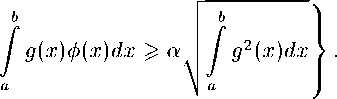
Рассмотрим следующую экстремальную задачу: для любой функции / Е ^[а^] найти

^/

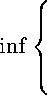
ъ

^^ -g^Ydx :

g Е М(ф, а) > .

Результаты пункта 2° позволяют сформулировать следующую теорему.

Теорема 2.4.1. Для любой функции / Е C’yy,] существует единственная непрерывная функция hf Е С*^], которая доставляет инфимум в задаче (3). При этом

если / Е М(ф, а);

df = <

(/« Р(хДх^, если / ф МДцД и / Е -М^ VI-аД,

«(fa №W

- (fa f^W^^V² - Vl - a² ff Дх)ф(хДх,

,               если J ф МДцоф и f ф —М^ф, \/1 — а²).

Функция hj равна /, если / Е М^ф,Д; hj равна 0, если / ф М^ф,Д и / Е — М^ф, V^ — а²),' если же / ф М(ф,а) и f ф —М^ф, V^ — а²), то

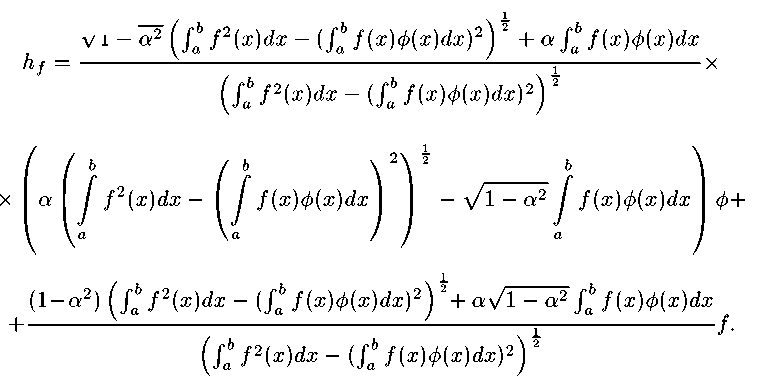
2\ 2