Равномерная триангуляция плоских областей
Автор: Клячин А.А.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика
Статья в выпуске: 2 (15), 2011 года.
Бесплатный доступ
В работе строится триангуляция элементарных областей и дается нижняя оценка минимального угла ее треугольников
Триангуляция, полярные координаты, элементарная область, липшицева функция, минимальный угол треугольника
Короткий адрес: https://sciup.org/14968688
IDR: 14968688 | УДК: 517.95
Текст научной статьи Равномерная триангуляция плоских областей
1. Общий подход
Пусть задан конечный набор точек { P i } N= 1 на плоскости. Триангуляцией набора точек называется набор треугольников { T j } M £1 , удовлетворяющих условиям:
1) любая точка Pi является вершиной хотя бы одного треугольника Tj ;
2) каждый треугольник Tj содержит только три точки из данного набора, являющиеся вершинами этого треугольника.
2. Элементарные области и их триангуляция
Пусть Q — ограниченная область в R 2 . Триангуляцией области Q называется триангуляция произвольного конечного набора точек, лежащего в замыкании области Ω.
В работе [5] приводятся алгоритмы построения триангуляции набора точек, которые могут быть применены и для построения триангуляций областей. Имеются и другие многочисленные работы, посвященные триангуляции плоских областей. Например, в работе [1] описывается алгоритм, основанный на разбиении области на такие подобласти, которые можно «разрезать» на полосы. Дальше получившиеся полосы разбиваются на треугольники, при этом происходит согласовывание выбора точек триангуляции для соседних полос. Другие подходы описаны в работах [2; 4]. Скажем, в первой из них приводится алгоритм, на первом шаге которого выбираются вершины триангуляции на границе области. На остальных шагах реализуется последовательное построение треугольников внутри области как бы по слоям, начиная с границы области.
В настоящей работе приводится достаточно простой в реализации алгоритм триангуляции плоской области и даются нижние оценки минимального угла треугольников триангуляции. Стоит отметить, что значение минимального угла треугольника не является лучшей характеристикой триангуляции. Более точной характеристикой является радиус описанной окружности (см. [3]).
Основная идея нашего алгоритма основана на разбиении на элементарные подобласти, удовлетворяющие определенным ограничениям. Триангуляция каждой из областей разбиения не представляет особого труда. При этом все подобласти разбиваются согласованно, то есть «склейка» триангуляции задается единым шаблоном триангуляции областей.
Рассмотрим область Q, которая имеет вид
Q = {(x,y) : ai < x < bi, ^(x) < y < ^(x)}, где ^(x) и ^(x) — заданные на отрезке [a1,b1] липшицевы функции. Далее полагаем b = inf (^(x) — ^(x)) > 0, M = xe[ai,bi]
sup (^(x) — ^(x)) < то , x e [ a i ,b i ]
L
= max sup xi,X2G[ai,b1]
Mx 1 )—^(x 2 ) | | x i - x 2 |
sup x i ,X 2 G [ a i ,b 1 ]
|#x 1 ) - 0(x2^ | x i - x 2 |
.
Пусть a 1 = x 0 < x 1 < x 2 < ... < x n = b 1 — разбиение отрезка [a 1 ,b 1 ]. Положим f T (x) = = t^ ( x ) + (1 — т )^(x). Разобьем отрезок [0,1] точками 0 = т 0 < т 1 < т 2 < ... < т т = 1 и в области Q рассмотрим сетку, задаваемую системой точек
A ij (x i ,y j ) = (x i ,f T j (x i )), i = 0, ...,n, j = 0,...,m.
Ясно, что все точки (x i , y j ) G Q. Разбивая одной из диагоналей все трапеции вида A ij A i +1 j A ij +1 A i +1 j +1 , где i = 0, ...n — 1, j = 0, ...,m — 1, получим триангуляцию области Q (см. рис. 1).
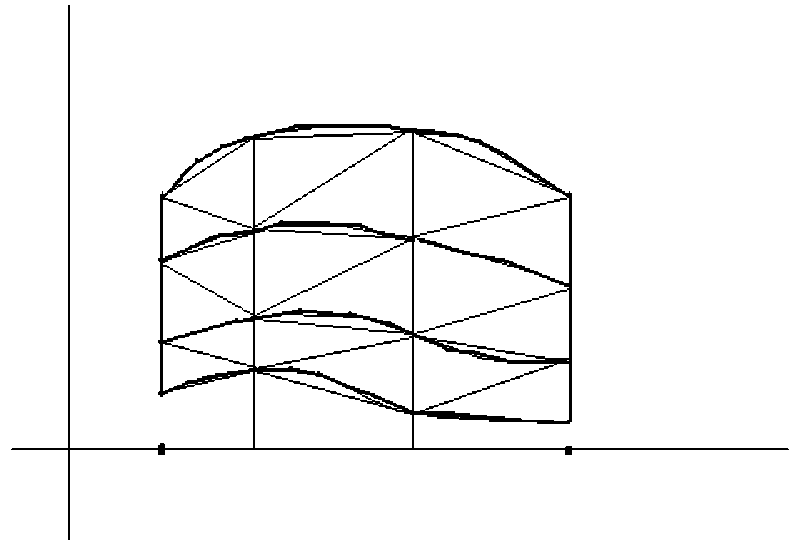
Рис. 1. Элементарная область в декартовой системе координат
Теорема 1. Для любого угла β всякого треугольника построенной триангуляции выполнено неравенство sin в >
min { 2 M8 , V T+ L } ^ (TlZL^I
Mδδ
= £ 1 L ,~b, h ,6 ,
где h = max (x i — x i - 1 ) , 6 = b max ( t — T j - 1 ) и 6 = b min ( t — T j - 1 ) . 1 < i < n 1 < j < m 1 < j < m
Далее рассмотрим область Q, которая представима в виде
Q = {(r, 9) : а < 9 < в, у(9) Пусть а = 90< 91<92 < ... < 9п = в — разбиение отрезка [а, в]. Положим gT(9) = = t^(9) + (1 — t)^(9). Разобьем отрезок [0,1] точками 0 = т0< t1< t2< ... < тт = 1 и в области Q рассмотрим сетку, задаваемую системой точек Bij(xij,yj) = (gTj (9i) cos 9i , gTj (9i) sin 9i), i = 0, ...,n, j = 0, ...,m. Ясно, что все точки (xij, yij) G Q. Разбивая одной из диагоналей все выпуклые четырехугольники вида BijBi+1jBij+1Bi+1j+1, где i = 0, ...n — 1, j = 0, ...,m — 1, получим триангуляцию области Q (см. рис. 2). Рис. 2. Элементарная область в полярной системе координат Введем следующие обозначения: Р = infШ9) —Н9)) > 0, R = sup (^(9) —Н9))< то; SG[a,e] 9е[а,в] р = inf ш(9\ > 0, R = 9G[a,e] V sup ^(9) < то; 9е[а,в] Л = max sup 91,92G[a,e] |^(91) —^(92) | |91 — 92| sup 91,92 е[а,в] И911—^(92 )| |91 — 92| Теорема 2. Для любого угла β всякого треугольника построенной триангуляции выполнено неравенство sin в ^ P min'll ПVR^l? ’ 1} 2^ (R + Л + R(n/()2+ R2 ηη = ^2 ( Л, P, P, R, R, £ , £ у , где £ = max (9i - 9i-1), n = min (t - Ti-1), n = max (t - Ti-1). 1<i<n 1<i<m 1<i<m
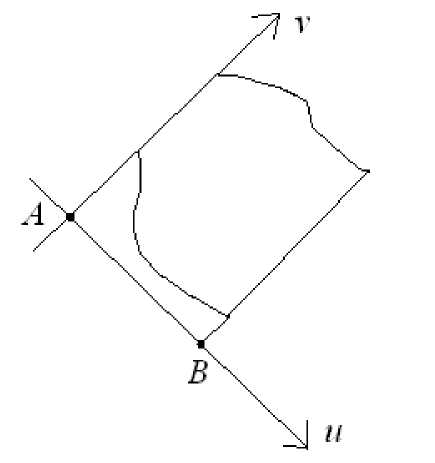
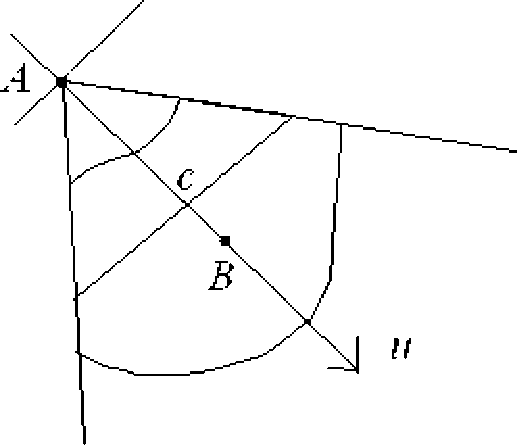
3. Триангуляция областей Элементарные области будем задавать следующим образом. Пусть A, B — некоторые точки плоскости. Рассмотрим систему координат (u,v), начало которой в точке A, ось Au направлена вдоль вектора A^B , а ось Av получается поворотом на угол п/2 оси Au против часовой стрелки (см. рис. 3). Рассмотрим отрезок [0, a] на оси Au такой, что точка B в координатах (u,v) равна (a, 0) и липшицевы функции ^(u) < ^(u) на этом отрезке. Тогда область первого вида Q — это множество точек, координаты (u, v) которых удовлетворяют условиям 0 < u < a, y(u)< v < ^(u). Рис. 3. Общее положение области первого вида Триангуляция данной области задается двумя наборами чисел ti = ui/a, i = 0,..., n, Tj,j = 0,..., m, причем 0 = t0 < t1 < ... < tn = 1. Аналогично описывается область Q второго вида. Для этого введем в плоскости (u,v) полярные координаты (r, 9). Пусть a G [0,п/4] и на отрезке [—а, а] заданы липшицевы функции 0 < ^(9) < ^(9). Тогда область Q есть множество точек (см. рис. 4), координаты (r, 6) которых удовлетворяют условию —а< 6< а, ^(6) < r< ^(6). Построим набор чисел {ti} и для таких областей. Рассмотрим отрезок, который задается равенствами u = c, —c tg а < v < c tg а, c> 0. Рис. 4. Описание области второго вида Пусть дано разбиение отрезка [—ctgа,ctgа] точками v0 = —ctgа < v1 < ... < vn = ctgа. Отметим, что этим точкам соответствуют углы 6i = arctg(vi/c), i = 0, ...,n. Тем самым триангуляция данной области задается двумя наборами чисел с tg а + vi ti = -----,i = 0, ...,n, Tj,j = 0, ...,m, 2c tg а причем, 0 = t0 < t1 < ... < tn = 1. Рассмотрим произвольную замкнутую область, которую мы можем представить в виде объединения конечного числа областей указанного выше вида Q = u1<k<NQk= Q1 U ... U nN. Среди этих областей есть области первого и второго типа. Пусть отрезок натурального ряда 1,...,N разбит на два непересекающихся множества I‘ и I‘‘, соответствующие областям первого и второго типов. Каждая из областей Ωk имеет границу, состоящую из четырех частей: Γ1k, Γ2k, Γ3k, Γ4k. Пусть Γ1kи Γ2k— боковые прямолинейные части границы, левая и правая, а Γ3k и Γ4k— описываются функциями ϕ и ψ , нижняя и верхняя. Будем предполагать, что пересечение границ областей Ωk и Ωl либо пусто, либо равно одному из Γsk. Считая, что все области Ωkудовлетворяют условиям либо теоремы 1, либо теоремы 2, введем соответствующие параметры областей: для к Е I‘ Mk , Lk , ak , bk , hk , δk , δk , и для к Е I‘‘ Λk , ρk, ρk , Rk , Rk , ck , αk , ξk , ηk, ηk . Зафиксируем k = 1, ..., N и наборы чисел {tk},i = 0,-.,n, Vk},j = 0, ...,m. Тогда, как было замечено выше, эти наборы чисел задают триангуляцию Rk области 9k. Обозначим через Vik, i = 0, ...,n, j = 0,...,m, вершины триангуляции Rk, а через T^, r = 1,..., 2mn — треугольники триангуляции Rk. Теорема 3. Пусть m = n и выполнены равенства tik = τik, tik = tli, k = 1, ..., N, i = 0, ..., n. Тогда совокупность всех треугольников Tkr, r = 1, ..., 2n2, k = 1, ..., N образует триангуляцию набора точек Nn и и vk ■ k=1 i,j=0 При этом для любого угла β всякого треугольника Tkr выполнено sin в > min (min |E1(Lk ■ bkk • ik ■ jk)} • mn {£2 (Лk■ pk ■ pk ■ Rk • Rk • nk ■ nk)}}. Замечание 1. Недостатком описанного способа триангуляции области является требование липшицевости функций, задающих нижнюю и верхнюю части границы элементарной области. Например, область, ограниченная астроидой, не задается липшице-выми функциями. Однако, как уже говорилось выше, в качестве характеристики триангуляции можно брать радиус описанной окружности треугольников. В этом случае допускается стремление угла β к нулю. Замечание 2. Описанный алгоритм переносится и на многомерные области. Для этого нужно выделить элементарные области, построить триангуляцию этих областей и оценить углы в тетраэдрах этой триангуляции.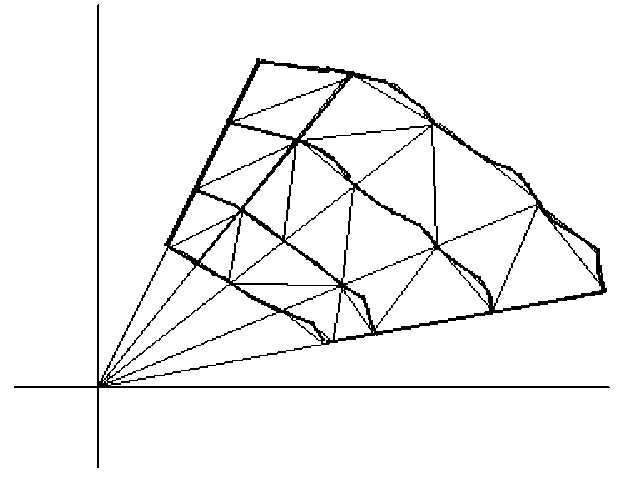
Список литературы Равномерная триангуляция плоских областей
- Алейников, С. М. Алгоритм генерации сетки в методе граничных элементов для плоских областей/С. М. Алейников, А. А. Седаев//Математическое моделирование. -1995. -T. 7, № 7. -C. 81-93.
- Галанин, М. П. Разработка и реализация алгоритмов трехмерной триангуляции сложных пространственных областей: итерационные методы/М. П. Галанин, И. А. Щеглов//Препринты ИПМ им. М.В. Келдыша. 2006. № 9. С. 1-32. URL: http://library.keldysh.ru/preprint.asp?id=2006-9
- Клячин, В. А. Аппроксимационные свойства триангуляции Делоне/В. А. Клячин,А. А. Широкий//Записки семинара Сверхмедленные процессы. -2010. -T. 5, № 5. -C. 8-14.
- Немировский, Ю. В. Автоматизированная триангуляция многосвязных областей со сгущением и разрежением узлов/Ю. В. Немировский, С. Ф. Пятаев//Вычислительные технологии. -2000. -T. 5, № 2. -C. 82-91.
- Скворцов, А. В. Триангуляция Делоне и ее применение/А. В. Скворцов. -Томск: Изд-во Том. ун-та, 2002. -128 c.


