Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

Случаи когда нули собственных значений лежат в комплексной плоскости рассматривались в работах [1, 2]. Если нули собственных значений принадлежат на числовой оси, тогда с помощью ранее используемыми методами [1, 2], мы не сможем исследовать решение сингулярно возмущенной задачи. Поэтому придется заново построить новый метод.

Рассмотрим конкретный пример и на основе этого примера построим метод. Цель исследования: доказать асимптотическую близость решений сингулярно возмущенных дифференциальных уравнений и соответствующих невозмущенных уравнений, в случае смены устойчивости на основе конкретного примера.

Материалы и методы исследования

Рассмотрим задачу

£ x '( t , £ ) = a ( t ) x ( t , £ ) + £ f ( t , x )                                               (1)

X(1 ₀ , £ ) = X° ( £ ) , x ⁰ ( £ )| = O( £ ) ,                                         ⁽²⁾

где a ( t ) = t - 1 , 0 <  £ — малый параметр, f ( t , x ( t , £ )) — аналитическая функция от двух переменных, t е T — конечный или бесконечный отрезок, 0 <  x <  5 , 5 — const . Например, f ( t , x ( t, £ )) могут оказаться многочленами относительно переменной x с аналитическими коэффициентами на отрезке T .

Невозмущенное уравнение a(t)x ( t ,0) = 0 имеет нулевое решение ~( t ) = 0 .

Собственное значение a ( t ) = t — 1 устойчиво при — w <  t <  1 , неустойчиво при 1 <  t < +® .

Для решения задачи (1), (2) x ( t , £ ) справедливо равенство

lim x ( t , £ ) = ~ ( t ) , £ ^0

при t е ( — w ,1 ) .

В данной работе доказывается , что равенство (3) имеет место для значений t е ( — w ,2 ] , то есть решение задачи (1), (2) задерживается на конечный промежуток времени t е [ 1,2 ] . Решение задачи (1), (2) не сразу уходит к бесконечности.

Теперь дифференциальную задачу (1), (2) заменим равносильной интегральной задачей

t

t

Г

t

x ( t , £ ) = x ⁰

( £ )exp ¹ J a ( s ) ds + j f ( t , x ( t , £ ))exp ¹ j a ( s ) ds d r . I ^£ ‘ 0          J 1 0                       V ^£ r          J

V

t 0

)

t 0

Уравнение (4) решим методом последовательных приближений x 0 ( t , £ ) = 0 ,

t

A

t

t

x j( t , £ ) = x ⁰( £ )exp — j a ( s ) ds + J f ( r ,0)exp — j a ( s ) ds d r , V ^£.        J 0             V ^£ T       J

V

J

)

t

t

t

A

x 2 ⁽ t , ^£ ) =

x ⁰( £ )exp — j a ( s ) ds + j f ( t , x_{ ( t , £ ))exp — j a ( s ) ds d r , V ^£ 1 0          J    10                       V ^£r         J

V

t ₀

J

t 0

... ... ...,

t

\

t

\- xn(t,£) = x (£)exp -ja(s)ds + jf(

V

t 0             J

if

if

о

t

^T , xn — 1

( r , £ ))exp ¹ j a ( s ) ds d r , V £ T        J

( n = 0,1,2,... ) .

Рассмотрим ряд

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №2. 2024 то

Е ^[ x n ⁽ t , ^£ ) - x n -1 ⁽ t ’ ^{£ ) ]} , n =1

Пусть  ~ ( t ) = 0 . Тогда не нарушая общности можно предположить, что

I x (0, £ )| = x 0 ( £ )| = O( £ ) .

Далее будем считать, что t = tx + it2; т = т + i^ , где tl, t2, т , т2 - действительные переменные. Тогда получим

j a (s) ds = j a (s)ds = -- t = 4(f - 1) - 1]=~[(t 1 - 1) - t 2 -1]+ it 2 (t 1 - 0, t о                   0

u ( t j, t ₂) = Re j a ( s ) ds = — [ t - 1)² - 1₂' — 1 ] .

0       2-

Справедлива оценка:

/

x ⁰ ( £ ) exp ¹ j a ( s ) ds   = O ( £ ) только при

I £ о        )

t

u ( t j, t ₂) <  0

Поэтому будем рассматривать

замкнутую область (рисунок 1) H_o = {( t j; t ₂): u ( t₁ , t₂ ) <  0 } .

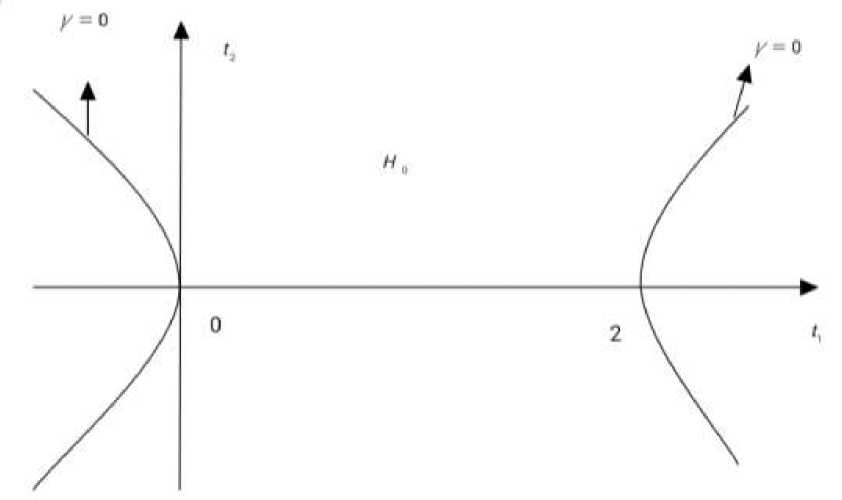
Рисунок 1. Область H .

Если ( t j, t ₂ ) e H _o, то x⁰

( ^{£ )ex}p ¹ j a ⁽ s ) ^d s l = O ^(£ ) ) .

t

\

X

Для того, чтобы последовательные приближения были ограниченными величинами необходимо выполнение условие u ( t_Y , t ₂) — u ( т , T ) <  0 то есть пути интегрирования должны быть убывающими от начальной точки до последней точки. Таким образом, пути интегрирования будем выбирать так, чтобы имело место неравенство

u(11,12) < u(т^Г2), от начальной точки до конечной точки (tl, t2). Это есть главное требование на выбор путей интегрирования для последовательных приближений. Для всех последовательных приближений пути интегрирования будут неизменными.

Пусть u ( 1 1 , 1 ₂ ) = / ( [ ( t 1 - 1 ) ² - 1 1

- 1 = 2 / 1 ) , где / — действительное число.

Если / >  0 , то гипербола будет расположена правее от особой критической линии

u ( t j, t ₂) = 0. Если - 1 <  / <  0 , то гипербола будет расположена левее от особой критической линии u ( t_l , t ₂) = 0 . Если / = - 1 то гипербола вырождается на прямые t₂ = ± (t_r - 1 ) . Если Y <- 1 , то гиперболы будет расположены вверх (вниз) между двух прямыми t₂ =± (t_r - 1 ) (Рисунок 2). Для любой гиперболы u ( t₁ , t ₂) = у прямой t₂ = ^ - 1 или t₂ = - t j + 1 является асимптотой.

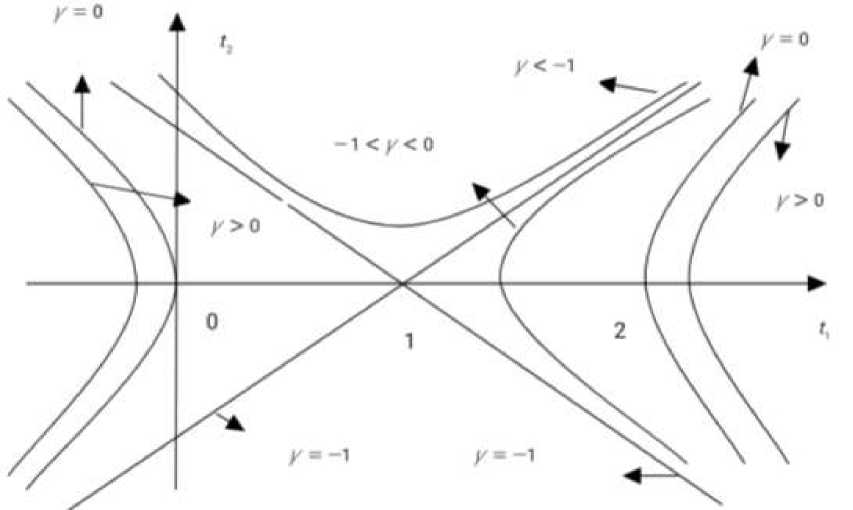
Рисунок 2. Линии уровня в области

H

Для нас особый интерес представляют поведения решения на отрезке 1 <  t _x<  2.

H — замкнутая бесконечная область, ограничена с левой стороны полупрямыми 1 ₂ = ± ( t 1 - 1 + S ) ) ( 1 <  1 1 < +^ ) , с правой стороны полупрямыми 1 ₂ = ± ( t 1 - 2 ) ( 2 < ^ < +w ) . (Рисунок 3).

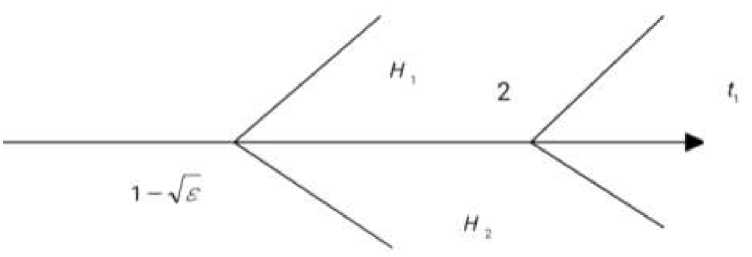
Рисунок 3. Области H и H .

H = H о H2 , где H = {(tx, t2 ) :(tx, t2 )e H и t2 > 0} , H2 = {t, t2 ) :(д, t2 )e H и t2 < 0} , H n H2 = [1 — Vs ,2]; H , H2 — симметрично относительно действительной оси Otx и обе является бесконечными областями.

T = { t i , t 2 ) :1 — S& <  t i <  1, 0 <  t^ <  t^ — 1 + V s } , T = { ( t j, t ₂) :1 — V s <  t_x <  1,0 <  t ₂<  t_x — 1 + 4 s], H 10 = H 1 \ T = {( t 1 , 1 2 ) : ( t 1 , 1 2 ) g H 1 , и 1 1 >  1 ] .

Решение задачи будем оценивать в замкнутой области H . Если пути интегрирования симметричны то сразу получим оценку решения задачи на H . Таким образом, будем оценивать решение задачи в области H . Сначала определим убывающей путь интегрирование для замкнутой области H .

Через Г обозначим множество точек гиперболы u(tx, t2) = 0 на плоскости, а через Гх обозначим правую половину гиперболы u(tx, t2) = 0 : Г = Г n H . Две линии гиперболы u (tx, t2) = 0 и прямой tx +12 = 2 пересекаются в единственной точке (2,0):

f u ( 1 1 , 1 2 ) = 0         f t — 1 ) ² — 1 ₂2 = 1

или Г ^{1   7    2}

t 1 ⁺ t 2    ²            t_x + 1₂ = 2

Запишем в виде

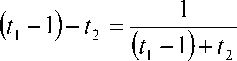
или Г

tx +12 — 2

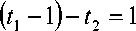
„ t j + t 2

= 2

Отсюда получим единственную точку пересечения двух линий (2,0). По вертикальной прямой точки гиперболы u(tx, t2) = 0 лежат выше (не ниже) чем соответствующие точки прямой tx +12 = 2 . Поэтому для точек гиперболы имеет место неравенство (tx —1) +12 > 1. Таким образом, для точек гиперболы Гх справедливо неравенство: из (^ — 1)2 — 12 = 1

1             1    , t — 1) —12 < 1. Отсюда tx — 2 < t2.

получим (tj — 1) —12 = -,----г---- < - = 1 или

^{( t} ! ^{— 1 )+} t 2     ¹

По вертикальной прямой точки гиперболы Г лежат выше ( не ниже), чем соответствующие точки прямой t_x — 1₂ = 2 ( ( t j — 1 ) — 1₂ = 1); по горизонтальной прямой точки гиперболы Г лежат левее чем соответствующие точки прямой.

Таким образом, рассмотрим прямую t2 = tx — 2 , по которой спускается + да (плюс бесконечность) до точки (д ,Т ), Т = t2, т = t2 + 2 , (д, t2) - конечная точка на области Их . По прямой т = т — 2 от начальной точки (2,0) до ( тх = +ю , т2 = т — 2 = +^ ) путь возрастающий. Нам нужен обратный путь. Следовательно, нужный нам путь будет убывающим. Далее от точки (т ,т ) = (ti + 2, t2) по горизонтальной прямой до точки (tx, t2). Это есть последний отрезок пути. l3 = {(т ,д ) т2 = t2; t2 + 2 > т > tx}. Таким образом, пути интегрирования для всех последовательных приближений будут неизменными: l = l0 о lx о l2 о l3 и I = /0 о ~ о ~ где

¹ 0 =^{{ ( т} 1 ^{, т} 2 ) ^:0 <  ^т 1 <  ^{1 —} ^т 2 = 0 ^} ,

11 = {(д, т2): т2 = д — 1 + Vs, 1 — Vs < д < +w],

³ = ^{{ ( t} i^{, t} 2 ) ^T 2 = ^T 1 ¹ 2 = ^{{( t} 1 , ^T 2 ) • ^T 2 = ^T 1

—

—

i+V£, 1—^£ — t —12+1—£}}, 2, 2 +12 — t < +^},

• ¹ 3 = ^{{( t} 1 ^{, T} 2 ) ^{: T} 2 = t 2 , t 2 ^{+ 2} ^ ^T 1 ^ t 1^} ,

3 = T, t ) • t = t2, t2 +1—£ — t — tt}.

Во всех выше указанных путях интегрирования условие (6) выполняется.

Теперь оценим последовательные приближения на замкнутом множестве H .

к

X j ( t , £ ) = x ⁰( £ )exp — J a ( s ) ds + J f ( T ,0)exp —J a ( s ) ds d r .

I£о       J о            к£т       J

t

t

/

t

Здесь Re J a ( s ) ds = — [ ( t j — 1 ) ² 2^L'-

Поэтому

—

1 2 — 1 ] = u ( 1 1 , 1 ₂) — 0 при ( t j , t ₂) e H = H о H₂ .

|A( t,£ ) =

x ⁰( £ )exp ¹ J a ( s ) ds  = O( £ ) при ( t _t, t ₂) e H . Остается оценить величины

t

A

t

к

/

о

J

t

\

t.

I ( t , £ ) = J f ( T ,0)exp -J a ( s ) ds d T .

к

T

J

Предположим, что | f ( т ,0)| = O (1) при t , t ₂ ) e H .

Если t , t ₂) e T то l = l ₀ о l ~ о l ₃. Тогда

1 1 ( t , £ )| = O (1) J exp |— ( u ( 1 1 , 1 ₂ ) — u ( t_pt ₂ ) ) j d T , где l = l₀ o l_Y o l₃ :

l 0 = ^{{ ( t} 1^{, t} 2 ) ^{:0 — T} 1 ^{— 1 —}

~ 1 =^{{ ( t} 1^{, t} 2 ) ^T 2 = ^T 1 ^{— 1 +} V i ,^{1 1} 3 = ^{{ ( t} 1 , ^T 2 ) • ^T 2 = t 2 , t 2 ^{+ 1 —} "^

£,T 2 = 0},

[ — £— — T — t2 + 1 — £} }, £ — T — t{ } .

1). Будем оценивать величины

l 0

Пусть l₀ = { ( t , T ) :0 — T — 1 — Тогда

'2 = 0 } .

^{u (} t 1 , t 2 ) ^{— u ( t} 1 , ^t 2 ) = 2^{[( t} 1 ^{— 1 ) 2 — ( t} 1 ^{— 1 ) 2 ]}= 2^{[( t} 1 ^{— T} 1 ^ t 1 ^{+ T} 1 ^{— 2 )]—}2^{[ (2} t 1 ^{— 2) ( t} 1 ^{— T} 1^{)] —} — — Utit— — t ) = V £ ( t — t i ) . Таким образом

к 1                            ^         t 1

J exp I   (u(tj, t2) — u(t ,T )||dT — J exp

10     к £                       J       0

к .£

— ^{( t} 1 ^— t 1 ) d ^T1 = ^£ exp

к £

J

к        ■' ]

к £ J

t 1

—

к

t 1

£ JJ

= о (k £ ).

Получена окончательная оценка f exp | —(u (tj, t2) - u (t ,T ))|’ W = O ().

к £                  )

l 0

• 2) . Рассмотрим интеграл

  exp I — ( u ( t j, t ₂) - u ( t

  
  
  
  
  

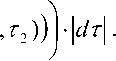
  Здесь ~ = { ( т , T ) : т

  
  

  ~ к ^s

  ^l 1

  
  
  

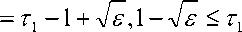
  < t^ + 1 — 2 s } .

  
  

  - u ^{( т} 1 ^{, т} 2 ) = -2^{[ ( т} 1 ^{— 1 ) 2 — T} 22 ^{— 1 ]}= ^iX l - 1 ) ^ + ^£ + ^{1 ]} .

[exp| —(u(tj,t2) — u(т,T))bIdT = a/2"exp| u(t1,t2) ~ к £                     )               к £ t^ +1—л/"£

■ j   ^exp

1— 4s

² 4s( Tx - ^{1 )+ £} + ¹

2 £

■ dr

)

Таким образом, получим оценку exp ( u(11,12) - u(r^rJ j d I = о(^£).

~1     к          £)

• 3) . Остается вычислить интеграл

exp(u(,,tt2)-u(r„r,)Y,

~s)

Здесь

• ^l 3 = ^{{( т} 1 , ^T 2 ) ^T 2 = t 2 , t 2 ^{+ 1} - 4s — ^T 1 — t 1 ^} ,

j exp ⁽ u ⁽ - ¹ , t ²)— u ^{T 1 T}— j d | = O (1) J exp - ¹—— ■ j d ^ |.

~3     к          £          )             t'     к      £)

^{T -1} _

Пусть — = s , тогда

V 2s t-, vst т = 1 + 42ss , dr = 2 2sds, r1 = 12 +1 — 2 s , Sj = 2 .—  < 0, T1 = 11 s2 =  .— < 0 и

2s sj < s2, — s = n, s = —n, ds = — dn, П = — si. n2 = — s2. Тогда

1 1 (t, 1 t, t s ) = O (1) j exp ⁽ - ^{( r} '   1 ) | dr, = SOO (1)f exp ( - s ’■ ) ds =

:    к     2s)

= - S^ O (1)Jexp ( - s² ) ds — SO O (1)Texp ( - n² d n .

n 1

Учтено интеграл Пуассона и получена оценка j exp ( u(11, t2) uT,rJ ^ ■ d| = O (^).

~3     к          s)

Если ( t j, t ₂) e H ₁₀ то l = l ₀ u l_r u l₂ u l ₃. Тогда

1 1 ( * , £ )| = O (1) J exp J — ( u ( * j, * ₂) — u ( t , T ) ) j| d T , где l = lo ^u 4 ^u h ^u I 3. ~    ^{к £                      7}

• 1) . Выше, оценка по пути интегрирования l получена.

• 2) . Рассмотрим интеграл

  ^£

  ^l1

  Здесь 4 = { t , T ) :1 — £ - T < +да , т = T

  
  

  —

  
  

  ^— u ^{( t} 1 ^{, T} 2 ) = ^{1 [ —(} T ^{— 1 ) 2 + T} 2 ^{2 +} 1 1 = ^{1 [ 2 (} T

  Пусть b — cons* , 1 — £ <  b < +да . Тогда

  J exp I — ( u ( * [, * ₂) — u ( t T ) ) ]• | d r | =

  / к ^£                       7

  
  

  —

  
  

  1 + V J } . )V £ + £ + 1 ] .

  
  

  b

  2 J exp

  
  

  u ( t_x , t₂ ) — u ( t , T )

  
  

  £

  
  

  d T =

  
  

  b

  2 J exp

  
  

  ² £ ⁽ T ^— 1) + ^£ + ¹

  
  

  к

  
  

  2 £

  
  
  
  

  • d T .

  
  

  Здесь оценка от величины b не зависит.

  
  

  Таким образом, получим оценку

  
  

  J ^exp

  
  

  u ⁽ t 1 , t 2 ) ^— u ^{( t} 1^{, T} 2 )

  
  

  £

  
  

  || d T = о (£).

  
  

  3). Теперь вычислим интеграл J exp

  l 2

  
  

  u ⁽ * 1 , * 2 ) ^— u ^{( T} 1 ^{, T} 2 ) 7

  
  

  £

  
  
  
  

  • d T где

  
  

  I 2 = {( * i , * 2 ) ^: + ^x >  T >  2 + *₂ , t = T — 2 } ,

  
  

  u ^{( t} 1 ^{, T} 2 ) = ^{1 [ (} T ^{— 1 ) 2}

  
  

  —

  
  

  ^T 2 ^{2 — 1 ]}= 2^{[( t} 1 ^{— 1 ) 2 — ( t} 1 ^{— 2 ) 2}

  
  

  ^{— 1 ]}= ^T 1 ^{— 2}.

  
  

  Пусть да >  b >  0, b — const . Рассмотрим интеграл

  
  

  1 2 + 2

  J ^exp

  b

  
  

  u ⁽ * 1 , * 2 ) ^— u ^{( t} 1^{, T} 2 )

  
  

  £

  
  

  • d T . Здесь

  
  

  ^T 2 = T

  
  

  —

  
  

  2, d ^ = d T , d T = 2d¹d T , u ( t , T ) = T — 2 .

  
  

  Поэтому

  
  

  1 2 + 2

  J ^exp

  b

  
  

  u ( t j, t ₂) — u ( t , T )

  
  

  £

  
  

  u ( * !, * ₂) ⁷ * ²+ ²      f 2 — T

  —¹      I I exp I       ¹ I d T .

  ^{£   7} ь     ^к 2 ^{£ 7}

  
  

  Таким образом, получена оценка

  
  

  J ^exP 1 2

  Остается вычислить интеграл

  
  

  u ⁽ * 1 , * 2 ) ^— u ^{( T} 1 ^{, T} 2 ) 7

  
  

  £

  
  
  
  

  • d T = O ( £ ) .

  
  

  J ^exp

  
  

  u ⁽ * 1 , * 2 ) ^{— u ( t} 1 T 2 )

  
  

  £

  
  

  • \dv\ .

  
  

  Здесь

  ¹ 3 = ^{{( t} 1^{, T} 2 ^T 2 = * 2 , * 2 ^{+ 2} ^ T ^ * 1 ^)} ,

  u ⁽ * 1 , * 2 ) ^— u ^{( T} 1 , ^T 2 ) = 2 ^{[ (} * ^{1 — 1 ) 2 — ( T} 1 ^{— 1 ) 2 ] - —(} * ^{1 — 1 ) T 1 —} * ¹ ) .

  
  

  Получен следующий интеграл

  f exp I — ( u ( t j, t ₂) — u ( т , т ) ]• \dt\ <  exp | ■

  k £                  7           V

  1 3          ⁴                                               l                 1 3          ⁴

  Рассмотрим два случая:

  • 1) . Пусть £ <  t j — 1 . Тогда при t — 1 — -7

  
  

  —

  
  

  ^ -^ ]• d T .

  £ 7

  
  

  £ , ПОЛуЧИМ

  
  

  I ^exP

  
  

  u ⁽ t 1 , t 2 ) ^{— u ( t} 1 T 2 ) 1

  
  

  £

  
  
  
  

  • 1,1    tГ I (tl — 1)(т

  • \di\ <  J exp I — ¹---— t 2+2      k            ^£

  
  

  —

  
  

  t 1 )

  
  

  £

  t 1 ^{— 1}

  
  

  _ I    ⁽ t 1 ^{— 1)(} t 2 ^— t 1 ^{+ 2)}

  exp I

  k           £

  
  

  — O ( ■£ ) .

  
  

  Или при t j — 1 >

  
  

  £ :

  
  

  I ^exp

  l ₃

  
  

  u ( t j, t ₂) — u ( t , T )

  
  

  £

  
  

  t г       f

  • | d T <  j exp I —

  t + 2      ^k

  
  

  ' ^{( т} 1     t 1

  £

  
  

  £

  t 1 ^{— 1}

  
  

ex, f   ( t 1 ^{— 1)(} t 2 ^— t 1 ⁺ 2)

^{— O} ( ^£ ) .

£

• 2) . Случай 1 <  t\ <  1 + £ . Тогда будем иметь

  I ^exp

  l 3

  
  

  u ( t j, t ₂) — u ( t , t )

  
  

  £

  
  

  t 1

  I d r\ — O (1) j exp

  ⁷                     t 2 + 2

  
  

  О т ^{— 1 )2} 1

  
  

  _—

  
  

  I     ^£

  
  
  
  

  • | d ^T i| ^—

  
  

  t 2 + 2

  ^{— O (1)} j ^exp

  t 1

  
  
  
  

  —

  
  

  12 A

  
  

  I      ^£   7

  
  

  ^d T .

  
  

Учтено, интеграл Пуассона и получено оценка

I exp l3

u ( t j, t ₂) — u ( t , t )

£

• \dt\ — o (£).

Теперь при любом (tt, t2 )е H , где H — H ou T, пути интегрирования будут такими как величина u (t{, t2) будет убывающими от точки t

—

( t i , 1 2 ) e H i , то

|x₁ ( t , £ )| — O (£ ) , причем эта оценка не улучшаемая.

£ ,0 ) до точки ( t j, t ₂) e H . Если

Для первого приближения x_{ ( t , £ ) справедлива оценка | x 1 ( t , £ )| — O (£) при ^{( t} 1 , t 2 ^)e H 1 . Таким образом, имеет место оценка, если (^, t ₂) е H , то

где 0 < c — const.

Таким образом, оценка (8) имеет место для всех точек замкнутой области H . Аналогично для области H имеет место оценка (8).

Теперь рассмотрим сходимости последовательных приближений . Если ( t j, t ₂ ) е H , то справедлива оценка

|x ( t , £ )| <  C £ , 0 <  c — const .                                      ⁽⁸⁾

В дальнейшем, положительные постоянные величины, которые в рассуждениях существенной роли не играют, и поэтому обозначим одной той же буквой C .

X 2 ( t , £ ) — X 1 ( t , £ ) = J f ( T , X j

l

г

t

'1( t , £ )) - f ( т ,О ) ] ехр - J a ( s ) ds d r . V ^£ T        J

Пусть

| f (t, x) - f (t, ~)| < вx — ~, где 0 < в — const.

Тогда |x2 (t, £) - x (t, £ )| < в J |x (t, £ )| exp | u (t— t2)—u (t-,t2) |. d^ < i             V         £J

• < вС£ J exp ( u ⁽ t ^- , t ^{2 )} - u ^{( T 1 , T 2} ) 1 \dv\ <  ( C£ 2 ) ² ;

i    V         £J

|X ₂( t , £ ) - X 1 ( t , £ )| < ( c £ ) .

В далее, имеет места оценка | x _n( t , £ ) - х _ич( t , £ )| <  ( с £ ) , ( n = 1,2,... ) .

Имеет места следующая теорема.

Теорема. На замкнутой области H задача (1),(2) имеет единственное решение x(t, £) , от представимое в виде x(t, £) = У[хя (t, £) - хяч(t, £)] и на H справедлива оценка n=1

| xn ⁽ t , ^£ ) ^- x n - 1 ⁽ t , ^£ ) < ^{( с} £: ^{) n} , ⁽ n

= 1,2,... ) где 0 <  c - const .

Результаты и обсуждения

Если нули собственных значений матрицы лежат в действительной оси, тогда случае смены устойчивости в точке линии уровня вырождаются, и область разделяется на четыре части. В трех из них не содержится неустойчивый отрезок t е [ 1,2 ] . Последняя часть области содержит этот отрезок. Трудность заключается в том, что переходить ту части область на конечном отрезке по убывающему пути интегрирования невозможно. Точнее, не существуют линии уровня соединяющую начальную и последнюю точку. Поэтому мы вынуждены разрабатывать новый метод для выбора пути интегрирования.

Вывод

Случаи, когда нули собственных значений лежат в действительной оси раньше не рассматривались. В работе доказано, что в этом случае тоже выполняется явление затягивания потери устойчивости.