Равномерно - разрывные подгруппы группы движений евклидова n - мерного пространства

Равномерно-разрывные подгруппы группы движений D используются для определения и изучения таких неевклидовых геометрий, о которых говорят, что они развертываются на евклидово пространство En . Прежде чем определять и изучать такие геометрии нужно исследовать и классифицировать все равномерно-разрывные подгруппы группы D.

Решению этого вопроса и посвящена данная статья.

Пусть En – n -мерное евклидово пространство и D группа его движений.

Определение 1 [ 1 ] . Группа движений G называется равномерно-разрывной , если существует такое положительное действительное число d , что для любого движения g е G и любой точки М евклидова пространства из условия M ^ g ( M) следует I Mg ( M) I >  d .

Простейшей равномерно-разрывной группой является тривиальная группа, состоящая только из тождественного движения.

Рассмотрим нетривиальные равномерно-разрывные группы.

Теорема 1 . Любое нетождественное движение из равномерно-разрывной группы движений евклидова пространства не имеет неподвижных точек.

Доказательство [ 1 ] . Пусть G - равномерно-разрывная группа, g е G и g ( М = М для некоторой точки М . Рассмотрим шар S = { N / Nm | <  d/^ }. Очевидно, g(S) = S. Тогда g(N) е S, поэтому Mg ( n )| <  d /. Следовательно,

Ng(N) I <  Nm\ + Mg ( N) I <  d .

Отсюда, по определению 1, N = g ( N ) для любой точки N e S . В шаре S есть (n + 1) внутренних некомпланарных точек, но движение пространства, имеющее (n + 1) неподвижную точку, является тождественным. Итак, если g имеет хотя бы одну неподвижную точку, то оно тождественное.

Теорема 2. Любое нетождественное движение из равномерно-разрывной группы G движений евклидова пространства можно представить в виде S_n • Т- , где а / /П_к и 1 <  к П _{к    а}

• < ( n — 1).

Доказательство. Всякое движение из D можно представить в виде произведения параллельного переноса и движения, имеющего хотя бы одну неподвижную точку (т.е. в виде g • T-_b , где g - движение, имеющее хотя бы одну неподвижную точку). При g = е получим параллельный перенос. Пусть g ^ е. Если b = 0 , то g • T- = g и не может входить в G.

Следовательно, b ^ 0 для всех элементов из G , отличных от параллельного переноса. Если движение g имеет только одну неподвижную точку, то при n >  2 оно является центральной симметрией. Но произведение центральной симметрии на параллельный перенос есть центральная симметрия, поэтому оно не может входить в группу G.

Следовательно, если g * е, то оно имеет к -плоскость двойных точек (1 <  к <  n -1) и вне этой плоскости двойных точек нет, т.е. g = S_n . Вектор b представим в виде суммы b = a 0 + a , где а 1 П_К, a ₀ X П_к или a₀ = 0 .

Тогда g • T = S_n • Т • Т . Так как ^{b        Пк    а} 0     ^а

^S П к ’ Т а = ^S п 1 , ^где П к И П к , ^то g • T = S П¹ • Ta , где а / /П к¹ . к

Теорема 3 . Любая нетривиальная равномерно-разрывная группа содержит нетривиальную инвариантную подгруппу параллельных переносов.

Доказательство. Пусть G нетривиальная равномерно-разрывная подгруппа группы D. Так как множество параллельных переносов из G замкнуто относительно умножения и отображение, обратное параллельному переносу, является тоже параллельным переносом, то это множество является подгруппой в G. Так как g-1 • T- • g = T . Пусть S„ • Т - любой a         b              Пк    а элемент из G. Тогда

( S П к • Т а ) ( ^S П к • Т а ) ^е G •

Но

^{( S} П к • ^Т а И ^S П к • Т а ) =

= ( ^S П к • ^SП к ) • (T a • Ta ) = e • T a^=T2a •

Итак, в группе G есть параллельные переносы. Пусть Т - группа всех содержащихся в G параллельных переносов. Если g е G и T- е Т, то g-1 • T- • g = T- е Т. Следовательно, a                          ab подгруппа параллельных переносов, входящая в G, будет в ней инвариантной подгруппой.

Теорема 4 . Равномерно-разрывная группа G 1 содержит только параллельные переносы на пропорциональные векторы тогда и только тогда, когда она циклическая.

Доказательство. ^ Пусть T е G 1 b

(b ^ 0) и пусть ab - все возможные векторы, для которых T е Gi. Если А - фиксирован-ab ная точка, T _(А) = Ai, то |ab| = ААi I > d, если a ^ 0. Если {...,A-2, A-i, A, Ai, A2, ...} - орбита точки А при действии группы Gi, то все точки орбиты расположатся на одной прямой. Зафиксируем на этой прямой интервал I длины R, содержащий точку А. Пусть в этот интервал попали к точек орбиты. Интервалы Ij c центрами в этих точках, длины которых равны d, не будут пересекаться. Очевидно, если интервал I с обеих сторон увеличить на %, то в него войдет столько же интервалов Ij, сколько и точек орбиты. Следовательно, к < R + d/ и число точек, попавших в интервал I, будет конечным. Выберем из этих точек ближайшую к А точку В (В ^ А). Пусть AB = a • Очевидно, T- е Gi. Все T - е Gi, где m е R.

a                  ma

Покажем, что этими параллельными переносами исчерпываются все элементы группы G i . По условию теоремы в группе G 1 содержатся только переносы на векторы a a . Пусть a = m + r , где 0 <  r <  1. Тогда T - = T - • T - . Если aa     ma ra

7 е Gi, то и T - е Gi. Если С = T - (А), то Taa                 ra                       ra либо С = А, либо С ближе к А, чем В, что невозможно.

Следовательно, ra = 0 , a ^ 0 , т.е. r = 0. Итак, группа G 1 состоит только из всех возможных переносов вида T , а поэтому является циклической группой: G 1 = { T- }.

^ Пусть G1 = {T-}, a ^ 0. Любой эле мент из G1 имеет вид T -. Если А - любая ma точка и А1 = T - (А), то А ^ А1 о m ^ 0. Но ma тогда |АА1= ma|>|a|. Так как |a| > 0, то группа G1 равномерно-разрывная.

Теорема 5 . Равномерно-разрывная группа G 2 содержит только параллельные переносы, ранг системы векторов которых равен к , тогда и только тогда, когда она равна прямому произведению к циклических групп.

Доказательство. ^ Зафиксируем произвольную точку А. Пусть A - орбита точки А при действии группы G2. Все точки орбиты будут лежать в одной к-плоскости П. Если зафиксировать точку В, не лежащую в плоскости П, то ее орбита будет лежать в к-плос-кости, параллельной П, и может быть получена из точек орбиты A параллельным перено- сом на вектор ab . Если А1 = T— (A) и

В ¹ = Т_Тв ( В ), то Аа ¹ 1 = ВВ 1 .

Пусть К - шар радиуса R с центром в точке А , содержащий хотя бы одну отличную от А точку ее орбиты. Для любой точки А 1 , лежащей в К , верно неравенство АА ¹ 1 >  d. Рассмотрим все возможные шары К ¹ радиуса d /, центрами которых являются точки из К . Очевидно, эти шары попарно не пересекаются. Следовательно, их число не превосходит отношение меры шара, полученного из К увеличением его радиуса на d/ к суммарной мере шаров из К 1 , т.е. не превосходит числа

п( R + d/^) n  2 n (R + %) n

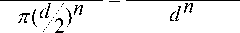
Так как полученное число конечное, то в шаре К лежит конечное число точек орбиты A. Выберем из них точку, ближайшую к точке А, и пусть она получается из А переносом на вектор а ₁ ( а ^ 0 ). Это будет вектор наименьшей длины из всех векторов, соответствующих переносам, входящим в группу G 2 . Очевидно, G 2 л { T- }. Так же, как и в теореме 3, ^а 1

можно доказать, что все переносы на векторы, пропорциональные a , образуют подгруппу { T- }. а

Расширим, если нужно, шар К так, чтобы в нем лежали хотя бы три точки орбиты A, не лежащие на одной прямой. В этом шаре тоже будет лежать конечное число точек этой орбиты. Через каждую точку проведем прямую, параллельную вектору a . Этих прямых будет конечное число. Пусть l э А и li - та из проведенных прямых, которая отлична от l и расположена ближе всех к прямой l. На прямой l1 внутри расширенного шара лежит лишь конечное число точек орбиты. Пусть С - ближайшая из них к точке А. Тогда в G2 есть параллельный перенос на вектор а^ = AC. Все параллельные переносы на векторы, пропорциональные а , образуют подгруппу {T }.

2                                          ^а 2

Очевидно, {T }n{T- }={е}. Если T- е G, и a 2           ai                              d d = «a + в«2, то легко показать, что ai = n, a2 = m. Следовательно,

G2эЬ }®{T- }.

V ^а1 ) a а 2 J

Если к >  2, то продолжая рассуждения, получим, что

G2 = T } ® T 1 ® ••• ® T }.

I ai )       \ а 2 J                   a а_к )

^ Пусть G 2 - T a } ® T ) ® • ® T a } , где векторы а , ( i = 1, 2, ..., k ) линейно независимы. Любой элемент из G 2 имеет вид T- ,

где g = пхах + па +... + nkak .

Этот вектор отличен от нулевого тогда и только тогда, когда n i , n 2 , ... , П к не равны нулю одновременно. Если А - произвольная точка и А 1 = T- ( A ), то

| AA\ | = |g| = ^а + п2а2 +... + пкак | >

> а[ + а2 +... + ак > 0.

Следовательно, группа G 2 равномерноразрывная.

Теорема 6 . Равномерно-разрывная групппа G 3 содержит винтовые движения только с одной и той же осью и не содержит параллельных переносов на векторы, не параллельные этой оси, тогда и только тогда, когда она является циклической группой.

Доказательство. ^ Пусть равномерноразрывная группа G3 содержит винтовые движения только с одной и той же осью и не содержит параллельных переносов на векторы, не параллельные этой оси. Пусть А0 про- извольная точка и В0 основание перпендикуляра, опущенного из этой точки на ось l. Рас- смотрим шар с центром в точке Во такого радиуса r, чтобы в нем содержались точка А0 и еще хотя бы одна точка орбиты А0. Пусть к -число точек орбиты А0, попавших в этот шар. Проведем открытые шары с центрами в этих точках радиуса

d 2

. Так как G 3 равномерно-

разрывная группа характеристики к, то эти шары не будут пересекаться. Все они будут содержаться в шаре с центром В0 радиуса 2п (r + d/)п r + dz . Следовательно, <   (   /2) , т.е. к

- целое число. Через каждую точку А р (0 < р <  к )

проведем гиперплоскость ур, перпендику лярную оси l. Из всех плоскостей Y, у2,..., ук выберем ту, которая ближе всех расположена к у0. Пусть это будет та плоскость, которая проходит через точку А1.

Обозначим       A A = a .      Тогда

A = Ra (A), Ra (A) G G4, т.е. в G4 входят I,a                    1 a °y все винтовые движения вида R nα , где n – l, na любые целые числа. Пусть R β - любое винтовое движение, входящее в G4. Пусть B0 ∈ l и B1 = R0- (Bo). Кроме того, обозначим Bi = Ra (B0), ..., Bn = A a (B0). Пусть В1 лежит между Вп и Bn+1 и. пусть Y1 э В 1, Y1 ^ l (рис. 1).

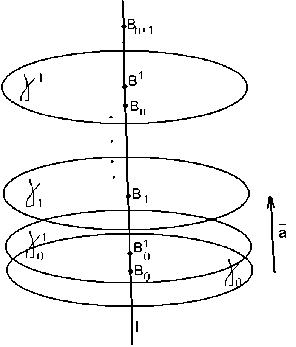
Рис. 1. Гиперплоскости, проходящие через точки В к

Рассмотрим R -nα . Это движение при-l,-na надлежит группе G3. Если B1 = R-na (B 1) и Y0 = Rl-na (х1), то Y0 лежит между Yo и Yi, что противоречит выбору γ1. Следовательно, B1 совпадает с Вn (или с Вn+1) и b=na . Если бы при этом было β ≠ nα, то в группу G3 входило бы движение

_R - n ε _{⋅ R} β _{= R} β - n α _{= R} β - n α _.

l , - na      l , na        l ,0              l

Если β ≠ nα, то в группе G3 будет содержаться нетождественный поворот вокруг оси, что невозможно. Итак, β = nα и все входящие в G4 винтовые движения имеют вид R nα . Следовательно, G = {Rα }. Если для l,na                                          3          l,a некоторого n найдется такое к, что nα = 2кπ, то Rnα = T и в группу G3 будут входить l,na      2na параллельные переносы T и винтовые движения Rt'2n+s)a , где 1 < 5 < n. l ,(2 n + s) a

Если G3 содержит параллельный перенос на вектор b , где bill, то легко показать, 2kn что при a =--- будет b = 2mna, в против- n ном случае b = 0. Но эти параллельные пере- g=te}.

носы содержатся в

е Пусть G = RaJ, пусть К-na п G3, n ≠ 0, А – произвольная точка и А1= Rnα (А).

l ,na

Тогда l AA l > | na | > | a |. Следовательно, группа G 3 – равномерно-разрывная.

Теорема 7 . Равномерно-разрывная группа G 4 содержит винтовые движения с к осями общего положения и не содержит параллельных переносов на векторы, не параллельные к- плоскости, параллельной этим осям, тогда и только тогда, когда она является произведением к циклических групп, изоморфных G 3 .

Доказательство. ⇒ Пусть G4 равно- мерно-разрывная группа и содержит винтовые движения с осями p1, р2, … , рк, не лежащими в одной (к-1)-плоскости. Тогда все винтовые движения с осью рs, входящие в G4, образуют циклическую подгруппу {Rαs } . Очевидно,

V p_s, as >

{Rαs } ∩ {Rαq }= {e}, если s ≠ q, ps - as          p aq - aq и            G4 = k {Rαs }.

l P s , a_s )

s = 1

⇐ Легко доказать, что группа

G 4 =   ^k { R ^{α s}  } , где { R ^{α s}  } ∩ { R ^{α q} } = { e }

Ps . as’            “ Ps, as)        Г Pq ■ aq )     1 J s =1

равномерно-разрывная.

Теорема 8. Равномерно-разрывная группа G5 содержит скользящие отражения только относительно одной к-плоскости и не содержит параллельных переносов на векто- ры, не параллельные этой плоскости, тогда и только тогда, когда она является либо цикли-

{STl_k , a ^}

ческой вида

дением

П S„^ ^} p = 1

, где a l Пг, либо произве- из m изоморфных цикли-

ческих групп, где 1 <  m ≤ k.

Доказательство. ⇒ Выделим в G 5 некоторую подгруппу Н, содержащую все скользящие отражения относительно плоскости П р , векторы которых пропорциональны между собой.

Пусть В о е П р . Проведем в плоскости П р шар К с центром в точке В о такого радиуса, чтобы в него попали отличные от В о точки ее орбиты при действии Н. Как и в теореме 3, можно доказать, что в этот круг попало только конечное число точек орбиты.

Пусть В 1 ближайшая из них к В о . Если S  ( Б _о) = Б, , то легко показать, что Н =

, ^a

{Sn -}. Если G5 = Н, то G5 циклическая, т.е. G5 = {S/z J’ где а 11 П. Группа G5 состоит из всех возможных скользящих отражений S,,,.,  - г                П ,(2 n+1) а и параллельных переносов Т^та, где n и m -любые целые числа.

Пусть G 5 , кроме подгруппы Н, содержит скользящие отражения относительно данн о й плоскости П на векторы, не параллельные а . Расширим, если нужно, круг К так, чтобы в него попали образы В о при таких отражениях. Так же, как и в теореме 3, можно доказать, что в круге К содержится конечное число точек орбиты точки В о при д ействии G 5 .

Пусть l_n э B_n , l n Il a , l n с П. Пусть 1 1 -ближайшая из них к 1 0 . Обозначим b = Б₀Б, . Тогда l ^SП , b (^с G 5 и G 5 = ^S П , a l ' l ^SП , b J . ^Очевидно, { S _П , _а } П ^{ S _П , b } = { е } . Группа G 5 ^состоит из всех возможных скользящих отражений вида S„ у, где из чисел к и р хотя бы

П,ka+pb ’                       г одно четное, и всех возможных параллельных переносов вида ТУ . -      .

¹                        (2 n + 1) а + (2 m + 1) b

Если G 5 содержит скользящие отражения на векторы, не равные ka + pb , то, продолжая рассуждения, аналогичные предыдущим, получим, что

G 5 = П ^S П , a p ^} .

р=1       p где векторы ар (1 < р < m) для любого 1 < m < (n— 1) линейно независимы.

^ Легко показать, что группы В -} и И, а

П S — }, где векторы а (1<р < m) линей-А      ilk ,ар /                          p p=1

но независимы, являются равномерноразрывными.

Теорема 9 . Равномерно-разрывная группа не может содержать скользящие отражения относительно двух не параллельных плоскостей.

Доказательство. Пусть равномерноразрывная группа G содержит скользящие отражения с плоскостями И 1 и П 2 и пусть И 1 п П 2 = 1.

Так как

Sn Г Sn- = T-b Sn, Sn, T =

П2, b    И a      b     21

Т ■ R2а ■ т = R2а, bl    а то, если S„ - е G и S„ 7 е G, то R2а е G, что И1 а                И2, b невозможно (следствие из теоремы 1).

Теорема 10. Равномерно-разрывная группа G содержит скользящие отражения относительно параллельных плоскостей тогда и только тогда, когда она является либо полупрямым произведением G 8 = { т } ^х { S _n -}, где И - одна из данных плоскостей, а II П, вектор b не параллелен П , либо полупрямым произведением

G9 = (Tb !®OX({S И, a }-Sn, g !)• где векторы а и g не коллинеарны и параллельны плоскости П, и векторы b и c, не коллинеарны и не параллельны плоскости П.

^ Если равномерно-разрывная группа G содержит скользящее отражение относительно плоскости П , то все скользящие отражения относительно этой плоскости, входящие в G , образуют либо подгруппу { S _n -}, либо подгруппу ^{{ s} _И , _а ^{} - { s} _И , b ^} - (теорема 7).

Пусть G содержит скользящее отражение относительно плоскости П 1 , где П 1 ^ П , но П 1 ЦП (пусть это S_n -, где p II П 1 ). Очевидно, G содержит движение ( S^ -■ S_n -) = Ta • S n • ^S П 1 ■ T p = T + p + -q , где q перпендикулярен плоскости П , направлен в сторону от П к П 1 и имеет длину, равную удвоенному расстоянию между И и И 1 . Обозначим b = а + p + q . Этот вектор не параллелен плоскости П. Следовательно, в первом случае G содержит параллельные переносы на векторы, коллинеарные вектору b . Они образуют циклическую подгруппу. Обозначим ее { Т } . Группа G содержит подгруппы { S ^ -} и T b ^} . ^Так как { S _n а } ⁿ { Т } = е и { Т } - инвариантна относительно ^{{ s} И , а ^} , ^то G 8 содержит ^{ T ^{} х { s} И , а ^} Очевидно, G 8 будет искомой группой.

Если G содержит подгруппу

{Sn}}'{^пj|, то она содержит движения {т} и {Т-}, где c, вектор наименьшей длины, па раллельный вектору g + p + q . Очевидно, векторы b и c неколлинеарны, подгруппа

(k } ® T ))

инвариантна относительно

S П , a J ' S П , i ! • ( S „а I S „ g I) M T ( ® T ^}) = е , следовательно, в этом случае

G 9 = ⁽ T ^}®^{ T F( S. „ , a I S „ ; I) .

^ Легко показать, что группы G 8 = { T-_b } ^ { s _{n fl} |, где a 11 П, а вектор b не параллелен плоскости П, и

G9 = ({Tb MT.|)X(S.„,a !'S „,g I)- где векторы a и g не коллинеарны и параллельны плоскости П, и векторы b и c , не коллинеарны и не параллельны плоскости П, а являются равномерно-разрывными.