Равновесные формы жидкости на внутренней поверхности вращающегося цилиндра и их устойчивость

Изучение форм равновесия вращающейся жидкости — классическая задача механики. Подробное изложение истории данной задачи дано в работах [1, 2].

Задачи ветвления и устойчивости форм равновесия для цилиндрического вращающегося жидкого столба рассмотрены в [3–6]. При этом в [3–5] исследованы плоские и осесимметричные формы равновесия, ответвляющиеся от тривиального состояния, в [6] показано, что существуют трехмерные нетривиальные формы равновесия.

В [7–10] изучалось движение жидкого слоя на внешней поверхности вращающегося цилиндра. При этом в [7] доказан принцип смены устойчивости в невесомости, в [8] — существование стационарного решения задачи со свободными границами в точной постановке и получено эволюционное уравнение динамики пленки в приближении тонкого слоя. Это уравнение позже анализировалось в [9]. В [10] плоская задача решалась численно в приближении тонкого слоя.

В [11–20] теоретически исследовалось движение вращающегося жидкого слоя, находящегося на внутренней поверхности цилиндрической полости. Вместе с тем, в работах [11, 12] не учитывались силы поверхностного натяжения; в [13, 14] изучалась плоская стационарная задача (в [13] рассмотрены случаи предельных значений числа Рейнольдса и малой толщины слоя, в [14] решение задачи осуществлено численно). В [15, 16] в приближении тонкого слоя проанализировано влияние поверхностного натяжения на устойчивость пленки в случае плоской задачи. Трехмерное течение на внутренней и внешней поверхностях цилиндра в приближении тонкого слоя рассмотрено в [17, 18]. В [19] также в приближении тонкого слоя исследовалась устойчивость плоского решения относительно малых осесимметричных возмущений, в [20] — устойчивость плоской стационарной жидкой пленки относительно трехмерных возмущений.

Экспериментально движение жидкого слоя на внутренней поверхности вращающегося цилиндра исследовалось в [21–25]. При этом в [21] наблюдалось формирование жидких колец внутри цилиндра. Влияние величины угловой скорости на устойчивость течения оценено в [22]. В [23] изучались устойчивость центрифугированного слоя маловязкой жидкости и влияние на нее инерционных волн. Устойчивости жидкого слоя при вибрациях посвящена работа [24], а [25] — динамике жидкости и сыпучей среды в быстро вращающемся цилиндре.

Как установлено в [26], от формы равновесия жидкости с цилиндрической свободной поверхностью могут ответвляться нетривиальные формы равновесия. Там же сформулировано условие ветвления в терминах бифуркационного числа Вебера. В работе [27] численно построены формы равновесия. Этот же результат в работе [28] получен автором независимо и практически одновременно с работой [27]. Следует заметить, что в [27] устойчивость равновесных форм не рассматривается.

В настоящей работе показано, что при увеличении отклонения числа Вебера от бифуркационного значения возможно изменение топологии равновесных форм в результате достижения ими или стенки, или оси цилиндра, а также исследована устойчивость форм равновесия.

Задача равновесия слоя жидкости на внутренней поверхности вращающегося цилиндра представляет не только теоретический, но и практический интерес. Например, она находит важное приложение в производстве пластиковых труб [29], технологические аспекты которого обсуждаются в [30]. Образующиеся на поверхности трубы неровности позволяют предположить, что течение неустойчиво. В [31] изучалась термокапиллярная неустойчивость жидкого слоя на внутренней поверхности вращающегося цилиндра. Как будет показано в предлагаемой вниманию работе, даже в изотермическом случае может возникать неустойчивость, обусловленная силами поверхностного натяжения. По аналогии с работой [7] рассматриваются осесимметричные возмущения как наиболее опасные. Задача сводится к определению форм равновесия жидкости методами теории бифуркации, устойчивость форм исследуется на основе обобщения теоремы Лагранжа об устойчивости [32] и ее обращения [33].

• 2.    Постановка задачи

  Рассмотрим находящуюся в

  
  

  цилиндрическую полость длиной L

  
  
  

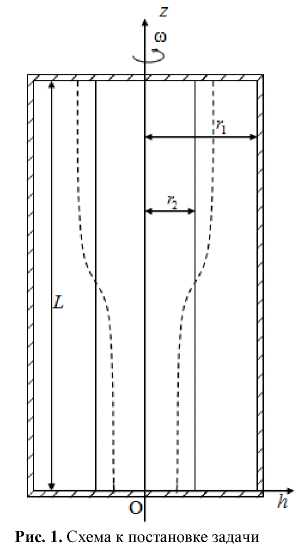
невесомости вязкую жидкость, которая частично заполняет и радиусом r1, вращающуюся с постоянной угловой скоростью ю вокруг оси z (Рис. 1). Если угол смачивания равен л/2, то существует состояние равновесия, при котором свободная поверхность также является цилиндрической с радиусом r < r [26].

Обезразмерим переменные, вводя в качестве масштабов длины, скорости и давления, соответственно, r ₂, ю r ₂ и рю ² r ₂², где р — плотность жидкости. Тогда независимыми безразмерными параметрами задачи становятся a = r 1 /г₂, 1 = L(r₂ , Re = ю r ₂ ² /v (число Рейнольдса) и We = рю ² r ₂ 3 /с (число Вебера). Здесь а — коэффициент поверхностного натяжения, v — вязкость жидкости.

В [26] доказано, что нетривиальные формы равновесия слоя жидкости на внутренней поверхности вращающегося цилиндра существуют только при 1 > п . Найдены бифуркационные значения числа Вебера We k , такие, что при We >  We k от цилиндрического состояния ответвляются нетривиальные формы:

We k = 1 - ( л/ 1 ) k ², k = 1,2,..., [ 1 /п ] . (1)

Здесь скобки [ ] означают целую часть числа.

Будем решать задачу в цилиндрической системе координат Ohфz, где z = 0 — одно из оснований полости, h = 0 — ось цилиндров. Отыщем формы равновесия вида: z = Z(h). На рисунке 1 нетривиальная форма равновесия схематически изображена штриховой линией.

Динамическое краевое условие в проекции на нормаль в случае равновесия имеет вид:

Ро — Р = -2 H с,

где p = ( h 2/ 2 ) + p₁ — давление жидкости, p 0 — атмосферное давление, p₁ — постоянная,

H = - ( ( 2 h )^{- 1} ( hZ 7 (1 + Z ' ² ) 1/ ² )

средняя кривизна поверхности. Здесь и далее штрих означает производную по аргументу h . Интегрируя (2), получаем

hZ '

We 4 c 1 2

--h +— h + c^ , 82²

1/2

(1+Z2)

где c ₁ и c ₂ — неизвестные постоянные. Обозначим через h ₀ и h ₁ наименьшее и наибольшее удаления формы равновесия от оси z соответственно. Тогда условие равенства угла смачивания п/2 запишется в виде:

Z ' ( h о ) = Z ' ( h i ) = » .                                                (4)

Объем жидкости, заключенной между цилиндрическими поверхностями равен:

– в невозмущенном состоянии п a21 -п 1,

– в возмущенном состоянии h1 пa21 -nJZ'h2dh . h0

Вследствие этого условие сохранения объема жидкости примет вид:

h ₁

J Z ' h ² dh = 1 .                                                 (5)

h ₀

Должно быть записано еще одно условие — это соотношение, задающее длину цилиндра, которая равна l :

h ₁

J Z 'dh = 1 .

h ₀

Уравнение (3) и условия (4)–(6) определяют двухпараметрическое семейство равновесных состояний.

• 3.    Построение форм равновесия

По аналогии с работой [5] введем независимые параметры:

h о        We ( 1 + 0 ) h 3i

.

0 = —, b =--------- h1                8

Из уравнения (3) и условий (4) выразим постоянные c и c ₂ через 0 , b и h 1 :

_ 2 ( 1 + b ( 1 + 0 ² ) )       _0 h 1 ( 1 - b 0 )

c ¹ =     h 1 ( 1 + 0 )     , c ² =      1 + 0 .

Разрешая (3) относительно Z', используя (8) и вводя новые переменные zh x =--, r =--, h1        h1

приходим к уравнению где

Отсюда

dX = V ( r , 0 , b ) , dr

r2 +0 + b (1 - r2)(r2-02)

V ( r , 0 , b ) = ,                             x Jx J .

1-1 -r2)(r2 -02)(1 -2b(r2 +0)-b2(1 -r2)(r2 -G2))

x = X ( r , 0 , b ) = j v ( t , 0 , b ) d t .

Из условий (5), (6) получаем

f1                  2 /f1Y h = I jv(t,0,b)dt| /I Jt2V(t,0,b)dt| , JJ f 1                    ^ ' /f 1

l = F ( 0 , b ) = J v ( t , 0 , b ) d t       j t ² V ( t , 0 , b ) d t

10             JJ

Равновесная форма параметрически определяется по заданным 0 и b с помощью выражений (12), (13) и формул

z = h X ( r , 0 , b ) , h = h r , 0< r <  1.

Построим формы равновесия, ответвляющиеся от тривиальной формы при наибольшем бифуркационном значении числа Вебера, вычисляемом по формуле (1) и равном We * = 1 -(л/ l ) ². Цилиндрическому состоянию равновесия соответствуют параметры: 0 = 0 * = 1, h ₁ = 1. Тогда из (7) имеем:

,. 1 С п² b = - 1 -т 4 1 l ²

Зафиксируем l и найдем зависимость b (0) . Пусть 0 0 , b 0 — некоторые значения параметров,

удовлетворяющие уравнению (14). После линеаризации (14) в окрестности 0 0 , b 0 получаем выражение

ь = bо

(0о-0НА(0о,bо ) +д0

Ц( ⁰ О , b o )

Полагая 0 = 0_Д = 0 0 - А0 , где А0 — некоторый малый параметр, устанавливаем приближенное решение уравнения (16), которое обозначим через b _А . С помощью линеаризации уравнения F ( 0_а , b ) - 1 = 0 в окрестности b _А приходим к формуле для уточнения корня:

Ь А = Ь А ⁺

( l - F ( 0 а , b а ) ) ⁵i ^{( 0} а • b а )

,

расчеты по которой длятся до момента, пока Ь > _а и b _а не совпадут с достаточной точностью. Сначала выбираем 0 0 = 0 * , b 0 = b * и находим корень уравнения (17). После установления b _а полагаем, что 0 0 = 0_А , b 0 = b _а , и повторяем описанную процедуру до тех пор, пока не дойдем до 0 = 0. Таким образом, получаем зависимость b (). Для построения равновесных форм как функций числа We на каждом шаге

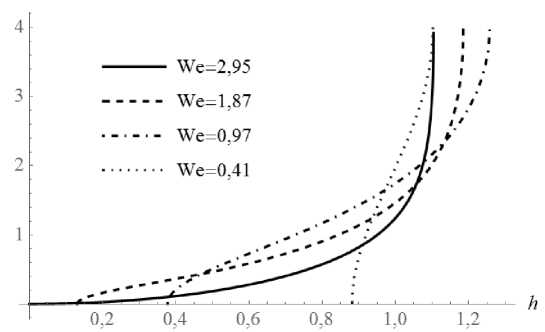
Рис. 2. Нетривиальные формы равновесия при различных значениях числа Вебера

по формулам (13) и (7) также вычислялись h 1 ( 9 ) и We ( 9 ) . Для численных расчетов взято l = 4, А9 = 10 2 , а А _А уточнялось по формуле (17) до выполнения неравенства ^А^ - А _А| <  10 -6 .

На рисунке 2 изображены нетривиальные формы равновесия, ответвляющиеся от тривиальной формы. Обнаружено значение We , при котором форма равновесия касается оси цилиндра. Заметим, что условие ветвления (1), а также уравнение (3) и условия (4)–(6) для определения равновесной формы не зависят от параметра a . Поэтому его можно задавать апостериорно, после выполнения вычислений, лишь бы форма не пересекала прямую h = a . Таким образом, возможно определение значения числа Вебера, при котором форма равновесия касается стенки цилиндра. В результате получено, что при a <  1,26 с увеличением значения числа Вебера форма касается стенки цилиндра, в то время как при a >  1,26 она доходит до оси цилиндра.

• 4.    Устойчивость форм равновесия

Обозначим через 5 отношение длины дуги равновесной формы, отсчитываемой от z = 0, к наибольшему удалению h ₁ формы равновесия от оси z . По определению

h

5 =

1j V1 + (Z ')"2dh.

h _{1 h 0}

Тогда из (9)–(11) следует, что r

5 = G (r) = (1 + 9) J т U (т, 9, А) d т, где и (r, 9, А ) =

(1 - r2)(r2 -92 )(1 - 2А (r2 +9)- А2 (1 - r2)(r2 -92))

Пусть N ( 5 , ф) — нормальная составляющая возмущения свободной поверхности, отнесенная к h 1 .

Исходя из принципа минимума потенциальной энергии [32], исследование устойчивости равновесной формы относительно возмущений, которые не смещают центр масс с оси вращения, состоит в поиске собственных значений следующей краевой задачи:

1 д r д 5

дN ) 1 д2 N r---- I--1--Y д5 J r2 дф

+ qh1 N + ц = XN при 0 < 5 < 51, 0 < ф < 2п,

дN

---= 0 при 5 = 0 , 5 = 5 , д 5

⁵ 1 2п                     ⁵ 1 2п

j j Nrd5d ф = j j

Nr cos

00         00

5 1 2п

фd5d ф = j j Nr sin фd5d Ф = 0.

Здесь: 5 , — значение 5 в точке пересечения равновесной формы с плоскостью z = l ; ц — постоянная; функция q определяется по формуле

q = 2 (V-n)H - 4H2 + 2K,

где K = Z 'Z 'Д h (1 + Z '2 )2)

гауссова кривизна, n

вектор внешней нормали к равновесной

поверхности.

Пусть Xmin — наименьшее собственное значение задачи (18)-(20). Согласно теории [32] при Xmin > 0 форма равновесия устойчива, а при Xmin < 0 неустойчива. Если подставить функцию N (s, ф) в задачу да

(18)-(20), представив ее в виде ряда N = Z0 (s) + ^(Zm (s)cosmФ + Vm (s)sinmф), то можно показать, что m=1

X min = min ( X ₀, X 1 ) . Здесь: X ₀ — наименьшее собственное число задачи

1 d | d ^ |—H rI-qZ0-Ц + XZ0 = 0 при 0 < s < si, r ds I ds 1

d Z„                                          sr

----= 0 при s = 0, s = s ,     [ Zo rds = 0 ;

ds

X 1 — наименьшее собственное число задачи

1 d ( dZ,) ri r^ I r ds ( ds /

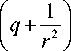
Zi +XZ1 = 0

при 0 <  s <  s 1 ,

d z   „

---= 0 при s = 0, s = s , ds

s ₁

J Z 1 rds = 0.

После преобразований из формулы (21) получаем

q =

2 mF

9 b ² r ⁴ +

92 (b 9-1)2

)- 8br2 (1 + b + b92 ) + (1 + 2b (1 -9 + 92) + b2 (1 + 492 +94))

Сначала исследуем устойчивость цилиндрического состояния. В этом случае 9 = 1, r = 1. С учетом этого спектральные задачи (22), (23) и (24), (25), соответственно, примут вид:

d -40- - q Z 0 -ц + XZ o = 0 при 0 <  s <  l , ds ²

— = 0 при s = 0, ds

l

s = l, J Z0ds = 0

и

d2Z. ,                  .

—V - ( q + 1 ) Z 1 +XZ 1 = 0 при 0 <  s <  l , ds ²

d ^ ¹ = 0 при s = 0, s = l ,   fZ! ds = 0.

ds                                 ₀

При решении данных задач получаем X ₀ = 4 b - 1, X 1 = 4 b , откуда следует X _min =X ₀ = 4 b - 1. Значит, при b >  1/4 цилиндрическое состояние устойчиво, а при b <  1)4 неустойчиво. Из формулы (15) вытекает, что при b <  b * имеет место неустойчивость цилиндрической равновесной формы жидкости. В таблице 1 приведены собственные значения для тривиальной формы равновесия при l = 4 в зависимости от разности We - We * .

Таблица 1. Наименьшие собственные значения для цилиндрической формы равновесия жидкости

We - We *	–0,34	0	0,02	0,62	1,62	3,62
X 0	–0,96	–0,62	–0,6	0	1,0	3,0

Теперь исследуем на устойчивость нетривиальные формы равновесия. В этом случае собственные значения задач (22), (23) и (24), (25) найдем численно с помощью метода Галёркина. Запишем полную систему функций, удовлетворяющих краевым условиям (23):

L , = 2 5 ³ - 3 5 ² 5 , — G ¹, L к = 5 ²( 5 — 5 , ) k —     , к = 2,3,...,

G0

где s1

Gо =| rd5 = (1 + 6)J r2 U (r, 6, b) dr, 0

s1

• G, = |(252 -3525,)rd5 = (1 + e)|r2 (2G3 (r)-3G(1)G2 (r))U(r,6,b)dr, о

• s1

Gk = J 52 (5 - 5, )k rd5 = (1 + 6) Jr2G2 (r)(G (r)- G (1)) U(r, 6, b)dr. 0

Будем искать решение задачи (22), (23) в виде

n

Z о =E fk L к ( 5 ). к=1

Из требования ортогональности функций L , , ..., L n левой части уравнения (22) получаем систему алгебраических уравнений

n

Х ( d-j +^х e j) f = 0 j = 1, 2,..., n , i =1

где

1 Г d L d L,                                         .1

du =- ( 1 +6 ) | 1 —^L — + qL - L j I r U ( r , 6 , b ) dr , e - j = ( 1 + 6 ) | L i L j r U ( r , 6 , b ) dr . ss

Приравнивая к нулю определитель системы (26), приходим к следующему уравнению:

d 1,1 + X e ,,

...

^dn ,1 ^+X e n ,1

^d 1, n ^+X e ,, n

d +X e n,n n,n

= 0,

отсюда находим значение X ₀, которое совпадает с наименьшим корнем данного уравнения.

Из реализации приведенного алгоритма для l = 4, n = 4 следует, что Х ₀ <  0 при всех допустимых значениях 6 и b . В таблице 2 представлены результаты расчетов Х ₀ для некоторых значений 6 и b , при этом соответствующие функции b ( 6 ) и We ( 6 ) были установлены в предыдущем разделе. Таким образом, формы равновесия, ответвляющиеся от цилиндрического состояния, неустойчивы при всех значениях числа Вебера.

Таблица 2. Наименьшие собственные значения для нетривиальных форм равновесия жидкости

θ	0,99	0,9	0,7	0,5	0,25	0.01
b	0,097	0,1	0,14	0,2	0.35	0,49
We - We *	0	0,01	0,06	0,2	0,76	2,41
X 0	–0,6	–0,67	–0,97	–1,8	–6,46	–14,9

Как и задача определения форм равновесия (3)–(6), задача (18)–(20), рассматривающая устойчивость этих форм, не зависит от числа Рейнольдса. На основании этого можно заключить, что неустойчивость возникает при сколь угодно малых значениях числа Re.

• 5.    Заключение

В работе построено полное семейство нетривиальных осесимметричных форм равновесия жидкого слоя на внутренней поверхности вращающегося цилиндра. Определение равновесных форм не зависит от толщины слоя, поэтому данный параметр задается апостериорно. При увеличении отклонения числа Вебера от бифуркационного значения форма жидкости касается стенки или оси цилиндра.

Равновесные состояния жидкости исследованы на устойчивость c помощью теоремы Лагранжа и ее обращения. Тривиальная форма равновесия неустойчива при значениях числа Вебера, меньших бифуркационного, а также при небольшом его превышении. При дальнейшем увеличении числа Вебера цилиндрическое состояние становится устойчивым. Нетривиальные формы равновесия, ответвляющиеся от цилиндрического состояния, неустойчивы при всех допустимых значениях числа Вебера.

Таким образом, в зависимости от значения числа Вебера можно выделить четыре характерные ситуации: 1) существует только тривиальная форма равновесия, и она неустойчива; 2) существует как нетривиальная форма равновесия, так и тривиальная, и они обе неустойчивы; 3) существует как нетривиальная форма равновесия, так и тривиальная, и лишь тривиальная форма устойчива; 4) существует только тривиальная форма равновесия, и она устойчива. В случае неустойчивости всех форм равновесия жидкости движение системы носит сложный нестационарный характер. Заметим, что в настоящей статье рассматривалась устойчивость относительно бесконечно малых возмущений. Из результатов работы [33] следует, что устойчивость форм равновесия относительно бесконечно малых возмущений влечет устойчивость к конечным возмущениям малой амплитуды. Вообще говоря, в случаях 3) и 4) тривиальная форма равновесия может быть неустойчива при конечных возмущениях большой амплитуды.

Существование и устойчивость форм равновесия жидкости в обсуждаемой задаче не зависят от вязкости, поэтому ветвление и неустойчивость возникают даже при малых значениях числа Рейнольдса, чего не наблюдается для вращающегося с постоянной скоростью цилиндрического слоя вязкой жидкости, заключенного между двумя твердыми стенками. Таким образом, можно заключить, что это происходит из-за наличия свободной поверхности.

Важно подчеркнуть, что анализ проводился для цилиндра конечной длины, но результаты данной работы применимы и для бесконечного цилиндра. В таком случае полученное решение продолжается периодически.

Автор выражает благодарность В.В. Пухначеву за внимание к работе, а также признателен анонимным рецензентам за замечания, которые позволили улучшить изложение результатов.

Работа выполнена при финансовой поддержке Совета по грантам Президента РФ для ведущих научных школ (грант НШ-8146.2016.1).