Различные инфляционные космологической модели с вращением

• A.    Введение

В данной работе мы рассмотриваем первую инфляционную стадию эволюции Вселенной для метрики типа IX по Бьянки для случая гибридной инфляции с двумя скалярными полями и вращением. В качестве источников гравитации на этапе инфляции используется анизотропная жидкость и два скалярных поля. Приведены ранее полученные решения [1] и [2] для моделей с хаотической и "новой"инфляцией, которые заполнены скалярным полем и анизотропной жидкостью. Сделана попытка понять, как выбор характера инфляции - хаотической инфляции, "новой инфляции"или гибридной инфляции - влияет на возможное вращение Вселенной в раннюю и современную эпоху.

• B.    Описание первой стадии инфляции в модели с гибридной инфляцией

В рамках общей теории относительности построен инфляционный сценарий с анизотропной космологической моделью с расширением и вращением с метрикой типа IX по Бьянки вида

• ² E-mail: panov@psu.ru

• ³ E-mail: kuvlenka@narod.ru

Здесь 〃 3 户 матричный элемент Лоренца, а, /3 = { 0, 1,2,3 } , 0 “ - ортонормированные 1-формы, которые связаны с масштабным фактором R через следующие соотношения:

0 0 = dt - R 〃 i £ 1 , 0 1 = RK i e 1 ,B² = RK 2 £ ² ,6» ³ = RK ₃ e^ ,                (B.2)

где имеются константы / > 0, K i > 0, K 2 = K 3 = ， K g — 〃 2 > 0.

Базовые 1-формы e * задаются в виде:

e1 = cosh(g) cos(z)d£ — sin(z)dg, e2 = cosh(g) sin(^)dT + cos(z)dg, e3 = sinh(y)dT + dz.

Источниками гравитации на этапе инфляции являются анизотропная жидкость и два скалярных поля.

Тензор энергии – импульса сопутствующей анизотропной жидкости в тетрадном представлении записывается в виде:

〃 b = (тг + 夕 ) U _a U _b +(cr — 7T ) 3 a 3 b - TT%*                          (B.3)

где тг, о это компоненты давления анизотропной жидкости, р это плотность энергии анизотропной жидкости, % = { 0,1,0, 0 } это проекция анизотропного 4-вектора на тетраду, u & = 帮 это вектор 4-скорости сопутствующей анизотропной жидкости, спроектированный на тетраду.

Тензор энергии – импульса скалярных полей в координатном представлении имеет вид:

T ab = 0 ,a 0 ,b + X ,a X ,b —

{ 2 (Ом 内 + ХмX ," 9“ — V(0,x )} 9 ab ,

(B.4)

(B.5)

(B.6)

(B.7)

а уравнения двух скалярных полей имеют вид

力*(f*0*)+do=0, у—9d (V—9产X,*) + dX = 0, с потенциалом вида

V(0,X ) = 2 ( g ² 。 ^{2 -} 〃 ² ) X 2 + T X 4    4 。 ⁴ + 2" ² 0 ² + K,

Для решения уравнений Клейна-Гордона-Фока найдем частные производные 翡 и 騎 ,и исследуем функцию V(О, X ) методами дифференциального исчисления на экстемальные точки.

Решая систему уравнений 翡 =0, 騎 =0, мы найдем три критические точки.

Точка максимума "式。 = 优 ,x = 0), V (M i ) = V 0 + 沐 .

Точка минимума M 2 ( 。 = 0, x = ^= ), V(M 2 ) = V 0 — 4^ .

Седловая точка М з ( 。 = 0,x = 0), V(M 3 ) = V 0 .

Идея гибридной инфляции состоит в том, что во время инфляционной стадии поле 。 велико, и система медленно скатывается вдоль долины х = 0. После того как долина х = 0 превращается в седло, происходит скатывание в перпендикулярном направлении, инфляция заканчивается, а осцилляции вблизи минимума М 2 (О = 0, х = у^), приводят к разогреву Вселенной.

Таким образом, мы считаем, что происходит медленное скатывание от точки максимума M i до седловой точки M 3 , а затем от седловой точки до точки минимума M 2 , где инфляция заканчивается. При этом потенциал поля V(О, х) равен нулю в точке M 2 , следовательно V o = 4^.

Тогда в рассматриваемой метрике система уравнений Эйнштейна имеет вид:

- (2 R+R2) K 12 +3 R 2 +у=р+V+ 亠

,

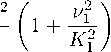
(B.8)

- (2R + I) +31K2 + 2 = 。- V + Т (1 + K|)'     (B.9)

(^2Л +1 ² ) (K 2 - ¹) - 4Kh ⁱ = L ^V + 鼻^ (^{1 -} K 2 )'        ( B.1⁰ )

(一 ^R 更［生       「( ^{ф 2} + % ² )

(R ⁺ R ² 丿 K ₁ ⁺ 2K 4 R ²        K ₁      .                    ⁽ . )

Таким образом, для нахождения неизвестных функций R = R«), ф = ф(^), % = %«) получим систему трех дифференциальных уравнений (с учетом (5), (6), (11)):

3 万 0+0+ л

2 X 2 g

0 =

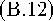
• ³    三大 + % + U X (g ² 0 ² + 九 i x ² - 4 ² ) = 0 . л  л ²     K i     (^{0 2} + X ² )

  (B.13)

  (B.14)

  
  

  - Л + Л ² + 4K 4 л ² =    2    .

Пусть Л = R _o e^Ht, тогда - 黄 + | 2 = 0, ( 0 ² + % ² ) = ₂ K 4 氤 2 Ht .

Выберем % = Сф, где С - некая константа. Тогда получим:

V 2 + 2С ² K 2 R o e ^H

(B.15)

(B.16)

СК 1

" 2 + 2c ² K 2 R o e ^H

Рассматриваем первый этап, когда система медленно скатывается вдоль долины % = 0 от точки максимума М1(ф = ^^, % = 0), V(М1) = V0 + ^^ до седловой точки М3(ф = 0,% = 0),

V(” 3 ) = V 0.                   ^{2                            2}

Условие медленного скатывания выполняется при

ф

³ 书 ф

« 1.

(B.17)

Тогда мы можем пренебречь второй производной ф и уравнение Клейна - Гордона - Фока (12) приобретает вид

• ³    л^ф + к 2 ^ф (^{g 2} % ² - 九 2 ^{ф 2} + 加 ² ) =⁰ .                        ( B.18 )

Решая уравнение (18) с учетом (15), мы получим:

— 3 炉      ^K 1       + K 2      ^К 1

" 2 + 2c ² K 2 R o e ^H  K 2 " 2 + 2c ² K 2 R q e ^H

((g ^{2 c 2} - " ² ) (2 + 2c ² ) K 4 R 0 e 2^H t + 加 ² ) = ^0.

(B.19)

Тогда из уравнения (19) получаем следующее соотношение между константами:

2     2 K 2       c ²

(B.20)

m² = 3Я² —2 ，九 2 = 丁.

K 2       g ²

Скатывание на втором этапе может быть как медленным, так и быстрым. Мы предполагаем, что происходит быстрое скатывание вдоль долины ф = 0 от седловой точки М з (ф = 0,% = 0), V(М 3 ) = V Q до точки минимума М ? (ф = 0,% = ^=), V(М 2 ) = 0.

Решаем уравнение Клейна - Гордона - Фока (13) с учетом (16), и получаем в результате:

- ₂ a 2     CK i      + 修      CK i

" 2 + 2C ² K 2 ² R ₀ e ^Ht    К ^ ^ 2 + 2C ² K^² R ₀ e ^Ht

( ( 9 2 + ^h 1 ^C 2 ) (2 + 2c 2 ) K 4 R 2 e 2 Ht - 〃 ² ) = ^0.

(B.21)

Тогда данное уравнение выполняется при

〃 ² = - 28 ² K 2 ， ^һ і = - c •

(B.22)

Мы можем сделать вывод, что скалярное поле х будет носить фантомный характер с мнимой массой 〃 = 勿 ^/3 т.

Окончательно получим:

Ф

K1.9

， 2д ² + 2h 2 K 2 R o e Ht K i " h 2

(B.23)

X =

У 29 2 + 2h 2 K 2 R o e ^Hi

Тогда из системы уравнений Эйнштейна мы находим плотность энергии

(B.24)

38 ² K 2

0 = -кТ

(B.25)

а также компоненты давления анизотропной жидкости

38 ² K 2      , 2K 2 - K 2

(B.26)

(B.27)

K 2   十 у 十 2K 4 R ² e ^{2 Ht} ,

• ^{38 2 K}l+ v +    ^K 2

K 2 十 у 十 2K 4 R ² e ^{2 Ht} ■

Таким образом, была построена модель первой инфляционной cтадии Вселенной с двумя скалярными полями и анизотропной жидкостью. Можно считать, что имеется одно комплексное скалярное поле, в духе работы [7].

После окончания первой инфляции энергия скалярного поля переходит в энергию рожденных частиц, а анизотропная инфлатонная жидкость переходит в темную энергию, которая наблюдается на современной стадии эволюции Вселенной.

• C. Описание первой стадии инфляции в моделях с хаотической и "новой"инфляцией

В духе работы [4], ранее нами были построены различные модели для метрики IX типа по Бьянки с разными видами инфляции. Приведем здесь решения для тех моделей, в которых в качестве источников гравитации мы взяли скалярное поле и анизотропную жидкость того же типа, что и в данной работе.

Модель хаотической инфляции была построена нами в работе [1].

Был найден масштабный фактор R = R«):

R = ^口 ；2 ch(8^)-

2^8 ky 2

Решение системы дается выражениями:

亓=。=—2-1 - 3H2 + у,(C.2)

^K 1

0 = --к2A + 3H2 - у.(C.3)

Потенциал скалярного поля в данной модели имеет вид: т ² ф 2

(C.4)

(C.5)

—2 , а скалярное поле мы находим в следующем виде:

К 2 E 2

ф = 0 0 (sh(H^ 3 K 2 H 2 .

Модель "новой"инфляции была построена нами в работе [2].

Одно из решений, представленных в работе [2], представляет собой космологическую модель для метрики типа IX по Бьянки, заполненную анизотропной жидкостью и скалярным полем. Найденный масштабный фактор для модели с "новой"инфляцией [2] полностью совпадает с масштабным фактором (28), ранее найденным для модели хаотической инфляции [1]. Решение системы уравнений Эйнштейна для модели "новой"инфляции [2], а именно, компоненты давления анизотропной жидкости тт, а, а также плотность энергии 夕 ,также совпадают с формулами (29), (30) для модели [1].

В отличие от модели хаотической инфляции, в модели "новой"инфляции мы предполагаем, что ф = Фо 尹,                                     (C.6)

а из уравнения скалярного поля мы находим потенциал V = V (ф) при k 《 H:

^V = K + _е^ф 2 - 8к^ф 0 ⁽ £声,

(C.7)

з н ² к 2 2 K 2

где £

На первой стадии инфляции для ообеих моделей мы считаем, что условия медленного скаты- вания выполняются.

D. Заключение

Нами были вычислены кинематические параметры моделей, описанных в этой работе. Сдвиг отсутствует. Параметры расширения, ускорения и вращения анизотропной жидкости (темной энергии) для моделей с "новой"инфляцией, хаотической инфляцией и гибридной инфляцией имеют одинаковый вид:

3 斤   左〃 i      匕

(D.1)

“= 五^, ° = ЁКІ № = 2Kp.

В духе работы [5] во всех перечисленных выше моделях мы считаем, что первая инфляция заканчивается при IO ^-35 C, а сразу после первой инфляции начинается радиационная стадия эволюции Вселенной. Поэтому можно состыковать составляющие анизотропной жидкости в конце первой инфляции и в начале ультрарелятивистской стадии. Эта работа была проделана в нашей статье [1] для хаотической инфляции.

Для моделей хаотической инфляции стадия расширения Вселенной длится ∼ 10-35 с и за это время Вселенная успевает увеличить свой размер минимум в 〜io100000 раз. Это приводит к тому, что в современную эпоху анизотропную жидкость можно считать практически не вращающейся.

Аналогично, в модели с "новой"инфляцией происходит увеличение характерного размера пузырька (Вселенной) с размера в момент его образования порядка 〜 1O ^-20 см до размера порядка 〜 1O ⁸⁰⁰ см после расширения, что намного больше размеров наблюдаемой части Вселенной 2 〜 10 ²⁸ см [3, 6]. То есть и для случая "новой"инфляции анизотропная жидкость, которой мы моделировали темную энергию в работе [2], в настоящее время не вращается.

В модели же с гибридной инфляцией с двумя скалярными полями и анизотропной жидкостью, построенной в данной работе, сохраняется возможность того, что если скорость вращения анизотропной жидкости в планковскую эпоху составляла 〜 10 43 с ^-1 , то в современную эпоху эта скорость может быть достаточно велика для будущих возможных наблюдений.