Разработка алгоритма генерации управляющей программы обработки винтовой поверхности шнека для станка с ЧПУ

Введение. Обычно при изготовлении шнеков различного назначения c винтовой канавкой сложного профиля для получения канавки используется фасонная фреза. Однако при мелкосерийном производстве такой подход представляется нецелесообразным вследствие высоких затрат на разработку и изготовление специализированного инструмента.

В данном случае можно использовать обработку канавки на станке с ЧПУ с помощью типового набора инструментов [1]. При реализации этой обработки возникает необходимость составления управляющей программы для станка с ЧПУ.

При разработке программы для обработки винтовой канавки шнека машины для грануляции полимеров (рис. 1) использование типовых ходов дало неудовлетворительные результаты. Управляющие программы (УП), созданные с помощью типовых стратегий для ротационной обработки в CAM-системах (computer aided manufacturing), являются неоптимальными. Они содержат большое количество холостых ходов и "лишних" перемещений, кроме того, структура программ не приспособлена к дальнейшему редактированию непосредственно на станке, так как винтовые ходы канавки подвергаются интерполяции и разбиваются на короткие участки. При изготовлении даже небольших партий указанные выше недостатки приводят к значительному увеличению общего времени обработки. Кроме того, не обеспечивается равномерность толщины фрезеруемого слоя в течение одного винтового хода, что вызывает ухудшение качества поверхности и снижение производительности [2].

Создание УП путем "ручного" программирования нерационально, так как требует большого объема математических вычислений и геометрических построений.

а

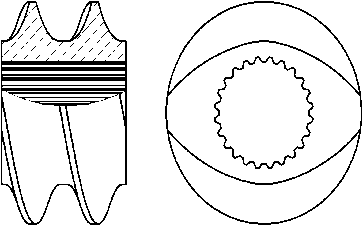
Рис. 1. Эскиз ( а ) и трехмерная модель ( б) шнека для переработки пластмасс

б

Целью работы являются разработка и реализация алгоритма формирования УП обработки винтовой поверхности шнека для станка с ЧПУ по заданному сечению, профилю канавки, числу заходов и ходу винта.

Для достижения данной цели необходимо решить следующие задачи:

• 1.    Разработка алгоритма выбора оптимального инструмента для черновой и чистовой обработки.

• 2.    Разработка алгоритма расчета траекторий движения инструмента при черновой и чистовой обработке.

• 3.    Реализация разработанных алгоритмов, обеспечивающая взаимодействие с системами САПР, применяемыми в машиностроении.

• 1.    Алгоритмы построения траекторий движения и выбора инструмента. Обработка винтовой поверхности шнека осуществляется на четырехкоординатном фрезерном станке следующим образом:

• 1.    Фреза позиционируется в плоскости XZ (далее профиль винтовой канавки определяется сечением плоскости XZ) станка в координатах, смещенных за пределы заготовки. Данное смешение необходимо для обеспечения плавного врезания фрезы.

• 2.    Совершается вращение поворотной осью A , согласованное с перемещением фрезы. При этом происходит удаление материала заготовки и формирование поверхности шнека. Поворот оси осуществляется с перебегом для обеспечения выхода инструмента из зоны резания.

• 3.    Инструмент перемещается в точку профиля на противоположной стенке канавки, и совершается обратный поворот.

Путем линейных преобразований можно получить программу для четырехкоординатного станка с любой другой схемой расположения осей.

Процесс обработки включает два этапа: 1) черновая, в результате которой удаляются основные объемы материала; 2) чистовая, в результате которой окончательно формируются необходимые форма и качество поверхности.

• 1.1.    Черновая обработка. При расчете траектории движения чернового инструмента необходимо дополнительно задать максимально допустимую высоту неровности профиля и припуск на чистовую обработку (рис. 2). Неровность возникает вследствие использования при черновой обработке концевых фрез, имеющих прямоугольный профиль сечения. Необходимо контроли-

• Рис. 2. Схема расположения припуска (1) и максимально допустимых неровностей профиля (2)

ровать высоту неровностей, так как при чистовой обработке они могут приводить к увеличению возникающих в процессе обработки вибраций, которые окажут негативное влияние на качество поверхности и стойкость инструмента.

Для нахождения опорных точек положения фрезы при черновой обработке предлагается использовать следующий алгоритм (рис. 3):

• 1.    В качестве текущей точки принимается начальная точка профиля.

• 2.    Из текущей точки строится вертикальная прямая, отстоящая от профиля канавки на заданную высоту неровности h в направлении оси Z .

• 3.    В точке пересечения вертикальной прямой и линии профиля (точка A ) строится горизонтальная прямая.

• 4.    В точке пересечения горизонтального отрезка и профиля (точка B ) строится вторая вертикальная прямая.

• 5.    Точки A и B сохраняются в массиве опорных точек.

• 6.    В качестве текущей точки выбирается точка A . Пункты 2-5 повторяются до завершения построения контура.

• 7.    По наименьшему расстоянию между последними опорными точками определяется максимально допустимый диаметр фрезы D _max.

• 8.    Из списка доступных инструментов выбирается фреза с наибольшим диаметром, не превышающим D _max. Выбранная фреза устанавливается в качестве используемой для обработки. Обозначим ее радиус R _инстр.

• 9.    На основе опорных точек путем смещения координат Y нечетных точек на положительное значение R _инстр, четных точек - на отрицательное значение вычисляется массив координат положений инструмента.

• 10.    Если расстояние между точками А и B больше 4 R _инстр , возникает необходимость в дополнительных рабочих ходах. Координаты этих ходов рассчитываются следующим образом.

• 11.    На основе координат формируется УП с использованием шаблона, включающего шапку программы и команды завершения. Тело программы создается путем дополнения команд перемещения инструмента в вычисленные координаты командами поворота оси A .

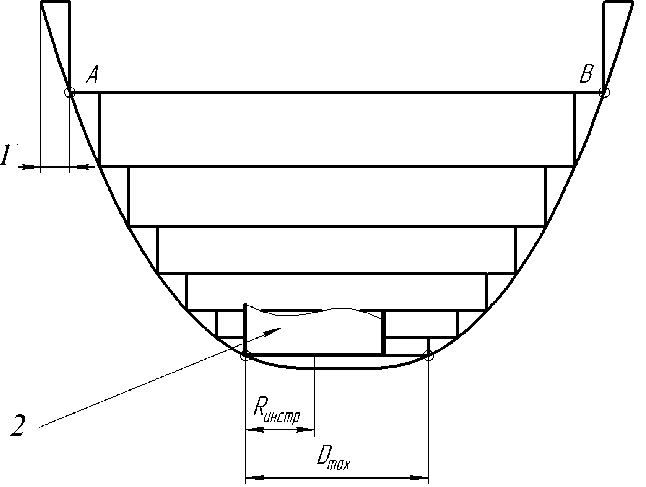
Рис. 3. Схема построения опорных точек положения фрезы при черновой обработке: 1 - высота неровностей профиля; 2 - фреза

Пусть B - массив координат положений инструмента,

В1 = А, В. = B, n Д( В. - В,)/ R „„тр J,

^В 2 = ^В 1 + ^{( В} . ^{— В} 1 ^{— 2 R} инстр ) / . , — , ^В . -1 = ^В п -2 + ( ^В . ^{— В} 1 ^{— 2 R} инстр ) / ..

• 1.2.    Чистовая обработка. Для чистовой обработки профиля используются радиусные фрезы, так как они позволяют обработать поверхность с меньшей высотой неровностей за меньшее число ходов. При чистовой обработке также возникает неровность профиля, обусловленная формой инструмента. Высота неровности может контролироваться, однако ее уменьшение приводит к увеличению числа ходов фрезы вдоль профиля и, следовательно, к увеличению времени обработки. Обозначим максимально допустимую высоту неровности профиля через h .

При определении используемого для обработки инструмента требуется найти фрезу с максимальным диаметром, способным обработать заданный профиль с указанной точностью без образования зарезов.

Для нахождения диаметра инструмента предлагается использовать следующий алгоритм:

• 1.    Строится эквидистанта на расстоянии h* (рис. 4, а ).

• 2.    Строятся эквидистанты соответствующие радиусам доступных фрез (рис. 4, б ).

• 3.    В точках перегибов контура строятся окружности с радиусами, равными радиусам доступных фрез (рис. 4, в ).

• 4.    По пересечениям эквидистанты максимально допустимой неровности профиля и окружностей выбираются радиусы фрез, подходящие для обработки данной канавки. При этом используется следующий критерий: окружность и эквидистанта максимально допустимой неровности профиля не должны пересекаться более двух раз, в противном случае это указывает на возникновение недореза при использовании инструмента с данным диаметром (рис. 4, д ).

• 5.    Среди возможных фрез, подобранных в п. 4, определяется фреза с наибольшим радиусом, которая принимается как используемая для обработки.

Для формирования УП чистовой обработки профиля винтовой канавки предлагается следующий алгоритм:

• 1.    В качестве текущей точки принимается начальная точка эквидистанты к обрабатываемому профилю (обозначим этот контур d) на расстоянии, равном R _инстр (рис. 4, г ).

• 2.    Текущая точка заносится в массив опорных точек. В текущей точке строится окружность радиусом R _инстр (см. рис. 4, г ).

• 3.    В точке пересечения окружности, построенной в п. 2, с эквидистантой профиля на расстоянии h формируется вспомогательная окружность радиусом R _инстр (рис. 4, е ).

  а

  
  
  

  б

  

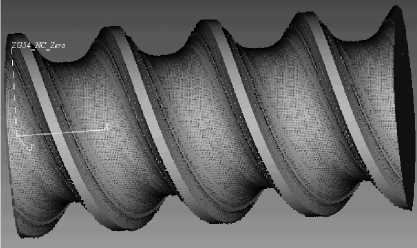
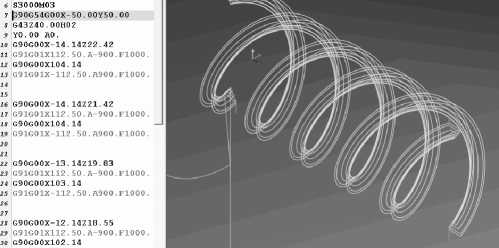
  Рис. 5. Фрагмент сформированной управляющей программы для шнека и траектории движения инструмента ( а ) и результат симуляции обработки на станке Haas VF3 ( б )

  
  

• 4.    Точка пересечения вспомогательной окружности и кривой d является новой текущей точкой (рис. 4, ж ).

• 5.    Пункты 2-4 повторяются до завершения построения контура d .

• 6.    На основе координат опорных точек формируется УП аналогично формированию УП для черновой обработки.

• 2.    Реализация и пример использования. При реализации предложенных алгоритмов создана прикладная библиотека для системы трехмерного моделирования и черчения KOMPAS 3D (компании АСКОН). Библиотека создавалась в среде программирования Borland Delphi на языке Object Pascal c использованием функций API KOMPAS 3D.

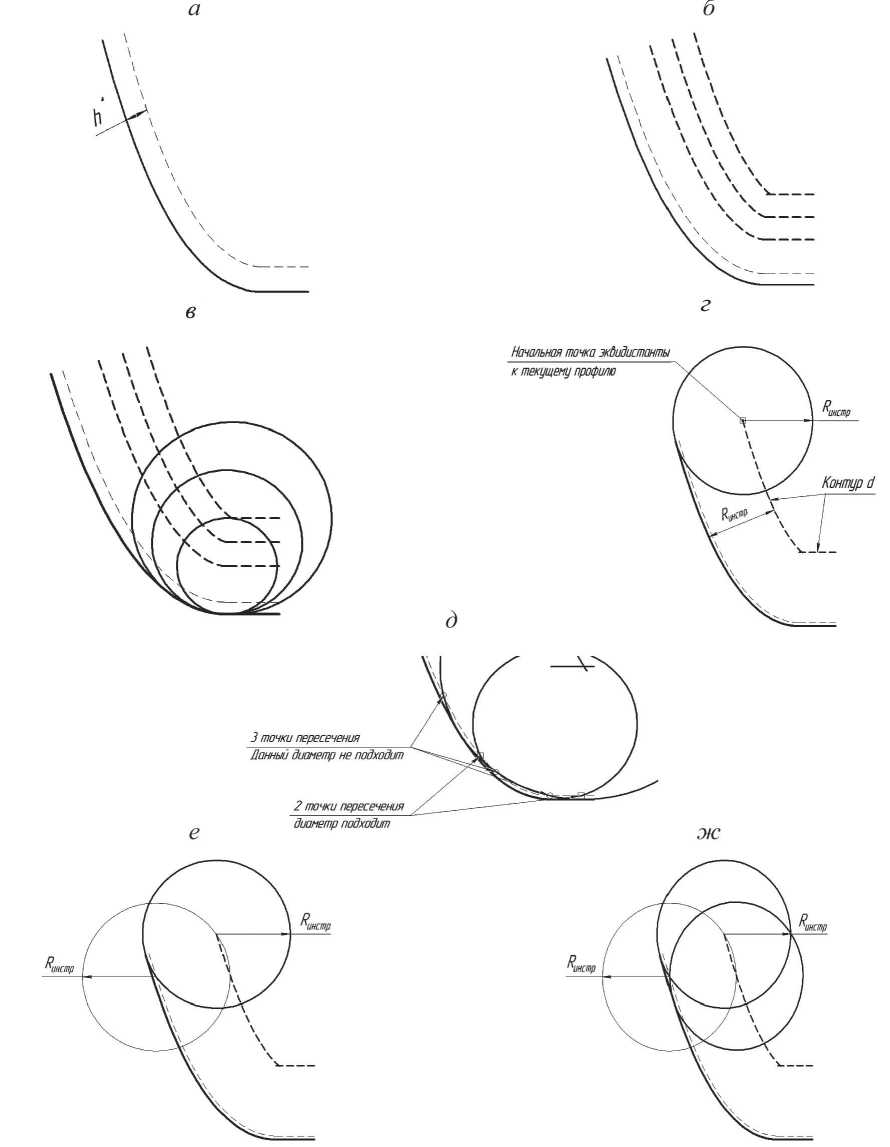
Рис. 4. Алгоритм чистовой обработки:

а - кривая допустимой погрешности профиля; б , в - эквидистанты, соответствующие доступным фрезам; г - схема определения начальной точки профиля; д - схема определения максимального диаметра фрезы; е , ж - схемы нахождения следующей точки профиля

Данный подход имеет большое количество преимуществ:

• -    отсутствует необходимость в импорте графической информации;

• -    используются функции геометрических построений системы KOMPAS;

• -    используется язык программирования высокого уровня для реализации алгоритма;

• -    используется графическая среда, привычная для пользователя-технолога.

На рис. 5 показаны фрагмент сформированной управляющей программы для шнека и траектории движения инструмента и результат симуляции обработки на станке Haas VF3. Выполненные измерения показывают правильность сгенерированной УП.