Разработка библиотеки встраиваемого программного кода для решения задач направленной кристаллизации

В настоящей работе представлена библиотека встраиваемого программного кода CrystarPack, реализованная в виде набора dll-библиотек, и предназначенная для решения задач направленной кристаллизации по методу Бриджмена. Заложенные в библиотеку методы определила методика, взятая из работ [1, 2], которая включает:

• •    использование преобразования физических координат в координаты равномерной прямоугольной сетки, что позволяет применять данный тип сеток при расчете меняющей свою форму области расплава;

• •    выбор преобразования координат таким образом, чтобы расчетная сетка сгущалась в пограничных слоях, формирующихся у границ области расплава;

• •    применение к дискретизации уравнений метода конечных объемов и полностью неявной схемы;

• •    решение получающейся системы нелинейных алгебраических уравнений методом Ньютона с численным нахождением элементов матрицы-якобиана на каждом шаге итерационного процесса.

Целью работы являются развитие и обобщение этой методики и ее реализация в виде написанной на языке Fortran 90 библиотеки встраиваемого программного кода. Библиотека позволит достаточно быстро и надежно создавать расчетные программы для задач направленной кристаллизации, снизить временные затраты на программирование и отладку, и, благодаря выполненному обобщению первоначально заложенных в нее методов, будет полезна для решения и других классов задач.

Создавая вычислительный код, разработчик выбирает численный метод, оставаясь относительно свободным в его программной реализации. Кроме того, код каждой расчетной программы, явно или неявно, включает некоторую часть, проистекающую из постановки решаемой задачи.

Написание вычислительного кода с использованием одного из традиционных для вычислительной математики языков программирования (Fortran, C и т.п.) требует, как правило, значительных временных затрат на программирование и отладку расчетной программы.

Возможным путем решения этой проблемы может быть построение обобщенной модели, пригодной для решения некоторого, достаточно широкого, класса задач и реализация методов данной модели в виде библиотеки встраиваемого программного кода. Очевидно, что данная библиотека должна включать в себя как реализацию выбранного для нее численного метода, так и механизмы связи методов библиотеки с постановочной частью расчетной программы.

Математически задачи механики сплошных сред обычно формулируются в виде систем дифференциальных уравнений в частных производных и соответствующих начальных и граничных условий. Процесс получения приближенного решения любой задачи условно можно разбить на этапы (Рис. 1).

На этапе 1 дифференциальные уравнения в частных производных, начальные и граничные условия формулируются в терминах физических полей, определяемых для физических переменных, в которых записывается модель решаемой задачи. Такой физический контекст сохраняется до этапа дискретизации, исчезая затем при получении системы алгебраических уравнений и ее численного решения. Вновь физический смысл проявляется на этапе вывода найденного решения задачи.

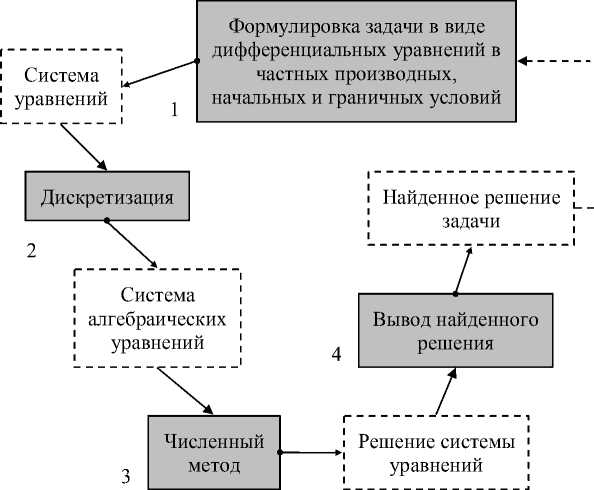
Рис. 1. Схема получения приближенного решения задачи

С одной стороны, имеется ряд описаний программных пакетов (DiffPack, FEAT, MUDPACK, см. [3]), реализующих численные методы решения систем дифференциальных уравнений в частных производных, получающихся, в частности, и при постановке задач механики сплошных сред. Входные данные таких пакетов, то есть системы решаемых дифференциальных уравнений, не имеют физического содержания и рассматриваются при работе пакета лишь в их математическом смысле. С другой стороны, создаются специализированные пакеты (ELMER, OpenFlower, ISAAC, Typhon, см. [4]) для решения какого-то конкретного класса задач, например, течений несжимаемой жидкости, газовой динамики, магнитной гидродинамики и т.п., которые не могут быть перенастроены на другой, отличный от заявленного, класс задач.

В отдельную группу следует выделить ряд коммерческих пакетов, например, FIDAP и FLUENT, предоставляющих исследователю широкие возможности для решения различного класса задач выбором подходящей модели из тех, что уже заложены в пакет. Но такой подход зачастую идет в ущерб гибкости в постановке задачи. Кроме того, многофункциональность таких пакетов напрямую связана с их высокой стоимостью.

Представляемая в настоящей работе библиотека занимает промежуточную нишу среди вышеуказанных типов программных продуктов: не являясь чисто математической, то есть позволяя включать в свою работу физический контекст, библиотека, тем не менее, может быть частью расчетных программ для различных классов задач. Это достигается исчерпывающим описанием точек вычислительного домена, в результате которого каждая точка получает свой «паспорт», однозначно выделяющий ее из прочих точек и передающий физическое содержание, сохраняемое и на этапе дискретизации уравнений решаемой задачи.

В результате становятся возможными отделение постановочной части расчетной программы от программной реализации численного метода и организация вычисления невязок от дискретизированных уравнений решаемой задачи в терминах, близких к постановке самой задачи.

Также следует заметить, что от программной реализации численного метода отделено не только физическое содержание, но и описание геометрии вычислительного домена, определяемое в постановочной части расчетной программы. Геометрический контекст, характеризующий точку домена, передается ее «паспортом» наряду с физическим содержанием.

Размер исходного кода библиотеки — 822 Кбайт (20–25 тысяч строк кода), количество основных процедур и функций — 135, общий размер исполняемого машинного кода — 1044 Кбайт.

Ниже описываются основные механизмы, включенные в код.

• 2.    Структура и основные механизмы

Представляемая библиотека выполнена в виде двух отдельных блоков: драйвера итерационного метода Ньютона и блока, реализующего процедуру вычисления интегралов, типичных для метода конечных объемов, с динамическим выбором нужного интеграла и свойств вычислительной схемы. Далее речь пойдет только об итерационном драйвере — наиболее оригинальной части библиотеки.

Итерационный драйвер состоит из менеджера решения, менеджера итерационного процесса и линейного решателя систем уравнений.

Программный код линейного решателя, основанный на методе обобщенных минимальных невязок — GMRES-методе (Generalized Minimal Residual) [5] с ILU-декомпозицией матрицы системы, взят из открытого источника в Интернете [6]. Ввод матрицы в решатель осуществляется в формате набора следующих «троек»: номер строки, номер столбца, величина ненулевого элемента. Оформленный в виде отдельной dll-библиотеки, используемый решатель можно заменить любым другим, имеющим тот же формат ввода-вывода.

Старт поиска решения задачи производится из менеджера итерационного процесса. Пользователь задает: тип итерационного процесса — для стационарной либо нестационарной задачи; необходимый размер объекта-решения — выделяемой в динамической памяти компьютера области заданного размера; число требуемых временных слоев; условия сходимости; период времени, для которого ищется численное решение; шаг по времени; шаг вывода найденного решения.

Ввод начального и вывод найденного решений задачи осуществляются вызовом процедур, предоставленных пользователем итерационного драйвера. Графические представления матрицы-якобиана и вектора-невязки могут выводиться на каждом шаге итераций в PostScript-файлы. Сводная информация о ходе итерационного процесса заносится в текстовый log-файл.

Вычисление невязок от дискретизированных уравнений решаемой задачи строится в итерационном драйвере с использованием ряда приемов:

• •    дискретизированное решение, взятое на отдельном временном слое, хранится в виде объекта-решения;

• •    объекты-решения создаются в менеджере решения по запросу менеджера

итерационного процесса согласно их необходимому размеру и числу требуемых временных слоев;

• •    адреса созданных объектов-решений предоставляются всем процедурам, так или иначе работающим с решением;

• •    доступ к элементу объекта-решения осуществляется по «паспорту» точки вычислительного домена посредством предоставляемых менеджером решения процедур;

• •     выбор кода, возвращающего вычисленную невязку, осуществляется по «паспорту»

точки вычислительного домена вызовом предоставленной пользователем драйвера процедуры;

• •    отображения номера переменной либо номера уравнения в «паспорт» точки вычислительного домена и наоборот осуществляются вызовом предоставленных пользователем драйвера процедур.

• 3.    Пример настройки драйвера

Таким образом, итерационный драйвер всегда определяет, от каких переменных зависит то или иное уравнение решаемой задачи, позволяя организовать динамическое вычисление матрицы-якобиана, необходимой для реализации итерационного метода Ньютона. Элементы матрицы находятся численно вариацией соответствующих переменных на управляемую драйвером малую величину. Предусмотрен выбор как простой конечной разности — левой, правой, центральной, так и вычисление ее с контролируемой точностью с помощью метода Рунге-Ромберга.

Часто более выгодным с точки зрения сходимости итерационного процесса является его расщепление на ряд отдельных подпроцессов, последовательно работающих с выбранными диапазонами переменных и уравнений решаемой задачи. Менеджер итерационного процесса предоставляет такую возможность. Благодаря механизму управления диапазонами переменных и уравнений, от которых в менеджере решения вычисляются элементы матрицы-якобиана, указанное расщепление может производиться в динамическом режиме.

Другим доступным механизмом, управляющим видом получаемой матрицы-якобиана и, косвенно, сходимостью итерационного процесса, является перенумерация переменных либо уравнений решаемой задачи путем занесения «паспортов»

соответствующих им точек вычислительного домена в предусмотренные для этих целей стеки нумерации (новый номер определяется позицией «паспорта» в стеке).

Итерационный драйвер не фиксирует тип используемых расчетных сеток. Однако упорядоченные сетки, в частности прямоугольные, здесь предпочтительнее неупорядоченных сеток. Расчет областей сложной или меняющейся формы (как, например, область расплава) может производиться с использованием либо преобразования физических координат в координаты сетки, либо предоставленного механизма исключения выбранных точек вычислительного домена из итерационного процесса (исключаются те узлы сеток, которые выходят за границы расчетных областей; для областей меняющейся формы может заблаговременно создаваться пул из таких узлов, по мере необходимости включающихся в итерационный процесс либо исключающихся из него).

В данном разделе приводится краткое описание приемов использования итерационного драйвера на примере задачи конвекции в квадратной полости при нагреве сбоку, сформулированной в терминах «функция тока — завихренность — температура».

Вся общая информация о решаемой задаче содержится в постановочной части расчетной программы. Для рассматриваемого здесь случая, это H — продольный размер квадратной полости, Th и Tc — температуры боковых стенок, Gr — число Грасгофа, N_eta и N_xi — линейные размеры прямоугольной сетки. Кроме того, определяется «флаг среды», который ссылается на жидкость в полости — Flag_liquid , а также три «флага поля» для ссылки на функцию тока, завихренность и температуру — Flag_SF , Flag_W и Flag_T соответственно. Имена «флагов» и их значения сами по себе не важны, а необходимы лишь для однозначного выделения соответствующей «среды» либо «поля» из прочих.

Определение параметров задачи конвекции в постановочной части расчетной программы имеет следующий вид real(8), parameter:: H = 1.D0

real(8) , parameter :: Th = 1.D0

real(8) , parameter :: Tc = 0.D0

real(8) , parameter :: Gr = 2000.D0

integer(4) , parameter :: N_eta = 20

integer(4) , parameter :: N_xi = 20

integer(4) , parameter :: Flag_liquid = 1

integer(4) , parameter :: Flag_SF = 1

integer(4) , parameter :: Flag_W = 2

integer(4) , parameter :: Flag_T = 3

Каждой точке вычислительного домена ставится в соответствие ее «паспорт» — номер переменной и номер уравнения решаемой задачи. «Паспорт» реализуется структурой, называемой «контейнером описания»

type Domain_point_type sequence integer(4):: medium integer(4):: field integer(4):: coord_1

integer(4) :: coord_2

integer(4) :: coord_3

integer(4):: point_kind integer(4):: max_order integer(4):: order integer(4):: info_1

integer(4) :: info_2

integer(4) :: info_3

real(8) :: info_4

real(8) :: info_5

real(8) :: info_6

end type Domain_point_type

Стандартный вычислительный домен представляется в виде набора прямоугольных (параллелепипедных) сеток. Пространственное расположение точки домена среди узлов сетки задается двумя (тремя) целочисленными координатами, для хранения которых служат поля coord_1 , coord_2 и coord_3 «контейнера описания».

Каждая из сеток получается дискретизацией пространства одной из сплошных сред, представленных в решаемой задаче (в занятом средой пространстве могут строиться одна либо несколько таких сеток с неперекрывающимися диапазонами координат). Точка вычислительного домена, принадлежащая одной из таких сеток, соотносится с соответствующей средой, получая «флаг среды», для хранения которого предусмотрено поле medium «контейнера описания».

Каждому набору «координаты сетки — «флаг среды»» соответствуют одна либо несколько точек вычислительного домена, различающихся «флагом поля» — физическими полями соответствующих точке элементов объектов-решений. «Флаг поля» хранится в поле field «контейнера описания».

Для модификации стандартного описания точки вычислительного домена служат поля info_1 , info_2 , info_3 , info_4 , info_5 и info_6 «контейнера описания». Если данных полей недостаточно, «контейнер описания» может быть расширен ссылкой на стороннюю структуру данных.

Поле point_kind «контейнера описания» определяет тип точки вычислительного домена по отношению к итерационному процессу и может иметь одно из трех следующих значений:

• •    значение 1 — точка участвует в итерационном процессе; соответствующие элементы объектов-решений хранят значения переменных решаемой задачи;

• •    значение 2 — точка исключается из итерационного процесса; соответствующие элементы объектов-решений предназначены для хранения постоянных значений;

• •    значение 3 — точка не участвует в итерационном процессе и по смыслу исключена из рассмотрения; соответствующие элементы объектов-решений всегда возвращают нулевые значения.

Вариант 1 является базовым выбором для большинства точек вычислительного домена; — 2 используется для реализации граничного условия; — 3 позволяет исключать некоторые точки из геометрии домена.

Поле order «контейнера описания» хранит номер переменной либо номер уравнения решаемой задачи, поле max_order — общее число точек вычислительного домена.

Соответствие «паспорта» точки вычислительного домена номеру переменной либо номеру уравнения решаемой задачи реализуют предоставленные пользователем итерационного драйвера процедуры для заполнения полей «контейнера описания» —

View_Order (point) . В общем случае требуются две таких процедуры, одна — для работы с номерами переменных, другая — с номерами уравнений.

«Контейнер описания» сообщается процедуре View_Order в ее аргументе point . Перед вызовом процедуры в «контейнере описания» заполняются либо поля, связанные с «паспортом» точки вычислительного домена; либо поле order , связанное с номером переменной либо номером уравнения решаемой задачи. Процедура должна поддерживать два режима работы: заполнение поля order на основании значений, связанных с «паспортом» полей, и наоборот.

Работа итерационного драйвера требует предоставленной пользователем процедуры вычисления невязки View_Residual (address_list, address, point, step, wish_step, residual) .

Аргумент residual процедуры View_Residual возвращает вычисленную невязку. Выбор вычисляющего невязку кода осуществляется по «паспорту» точки вычислительного домена, сообщаемому в «контейнере описания» point .

Вычисляющий невязку код пишется с использованием процедур итерационного драйвера для доступа к элементу объекта-решения. В рассматриваемом случае прямоугольной сетки такой доступ осуществляется посредством функции Point_Value_2D (address, medium, field, eta, xi) (подобные функции доступа реализованы также для случая параллелепипедных сеток и случая вычислительного домена общего вида). Здесь аргумент address указывает адрес объекта-решения, аргумент medium — «флаг среды», аргумент field — «флаг поля», аргументы eta и xi — координаты прямоугольной сетки.

Адреса объектов-решений хранятся в структуре, называемой «контейнером адресов»

type Solution_layer_type sequence integer(4):: task_type integer(4):: N_layer integer(4), dimension(1:10):: layer end type Solution_layer_type

Значение поля task_type «контейнера адресов» сообщает тип итерационного процесса, выполняемого драйвером: значение 0 — стационарная, значение 1 — нестационарная задача. Значение поля N_layer указывает число доступных временных слоев. Целочисленный массив layer хранит адреса объектов-решений в указанном N_layer количестве, в порядке увеличения времени решения. Для стационарной задачи требуется единственный временной слой.

«Контейнер адресов» предоставляется процедуре View_Residual в ее аргументе address_list в виде ссылки. Адрес объекта-решения на главном временном слое сообщается также отдельно в аргументе address .

Аргументы step и wish_step работают с шагом по времени — аргумент step сообщает текущий шаг, установленный итерационным драйвером, а аргумент wish_step позволяет задать желаемый шаг для последующих итераций. Для случая стационарной задачи данные аргументы не используются.

Задавая в итерационном драйвере требуемое число временных слоев и используя значения элементов объектов-решений, взятых на предоставленных временных слоях, можно реализовать вычислительную схему требуемой степени явности. Элементы матрицы-якобиана динамически вычисляются от решения на главном временном слое.

Время, связанное с объектом-решением, можно узнать вызовом функции итерационного драйвера — Solution_Time (address) , где аргумент address указывает адрес объекта-решения.

Ввод начального решения задачи осуществляется вызовом предоставленной пользователем итерационного драйвера процедуры Set_Solution (address_list, time) . «Контейнер адресов» предоставляется процедуре в ее аргументе address_list в виде ссылки. Аргумент time сообщает начальное время, заданное в итерационном драйвере.

Для установки элемента объекта-решения используются соответствующие процедуры итерационного драйвера. В рассматриваемом случае прямоугольной сетки — это процедура Set_Point_Value_2D (address, medium, field, eta, xi, value) (подобные процедуры установки реализованы также для случая параллелепипедных сеток и случая вычислительного домена общего вида). Здесь аргументы address , medium , field , eta и xi имеют то же назначение, что и соответствующие аргументы вышеупомянутой функции Point_Value_2D , аргумент value задает желаемую величину устанавливаемого элемента.

Вывод найденного решения задачи осуществляется вызовом предоставленной пользователем итерационного драйвера процедуры View_Solution (address, number, time) . Применяемый в процедуре формат вывода решения полностью определяется пользователем. Аргумент address сообщает адрес выводимого объекта-решения, аргумент number — номер вывода, аргумент time — связанное с решением время.

Когда все предварительные шаги сделаны и адреса подготовленных пользователем процедур сообщены итерационному драйверу, драйвер запускает итерационный процесс, в котором, как описано выше, пользователь имеет возможность задать: тип итерационного процесса (стационарный либо нестационарный); необходимый размер объекта-решения; число требуемых временных слоев; условия сходимости; период времени, для которого ищется численное решение задачи; шаг по времени; шаг вывода найденного решения. Важно, чтобы заданный тип итерационного процесса и число требуемых временных слоев соотносились с вычислительной схемой, реализованной в процедуре вычисления невязки, а требуемый размер объекта-решения соответствовал числу точек вычислительного домена.

• 4.    Тестирование

Приемы использования итерационного драйвера не связаны с видом уравнений решаемой задачи, что позволяет, без ограничения общности проводимой проверки, протестировать его на достаточно простых задачах с хорошо известными решениями.

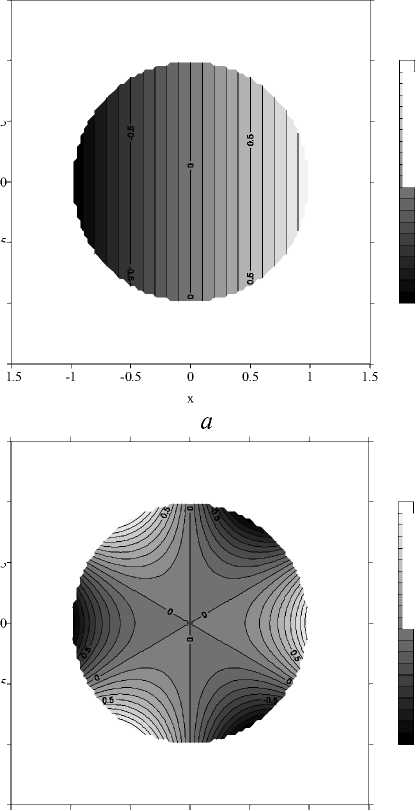
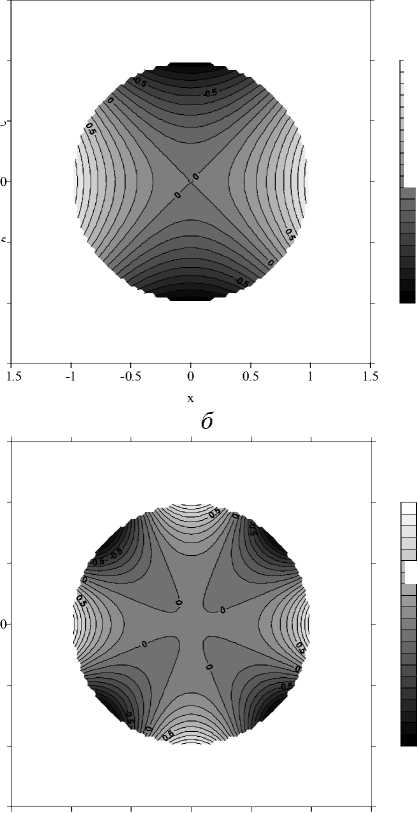
В качестве тестового выбрано решение уравнения Лапласа А ф = 0 внутри круга 0 <  r <  1. На границе круга ставилось граничное условие типа Дирихле ф | r _{= 1} = cos ( m3 ) , где m ^ N , r и 3 — радиальная и азимутальная координаты соответственно. При выполнении данного условия внутри круга существует единственное решение задачи ф = r^m cos ( m 3 ) .

Для дискретизации квадрата { - 1,5 <  x <  1,5; - 1,5 <  у <  1,5 } использовалась равномерная прямоугольная расчетная сетка 100 х 100 узлов. В прямоугольных координатах круг, где ищется решение задачи, задавался условием x ² + у ² <  1. Все точки сетки, лежащие вне данного круга, исключались из итерационного процесса.

В точках сетки, для которых 0,9 <  x ² + у ² <  1, невязка вычислялась как разность приближенного и точного решений задачи. Таким образом моделировалось граничное условие. Наконец, в точках сетки, для которых x ² + у ² <  0,9, невязка вычислялась от дискретизированного уравнения Лапласа.

Нелинейность уравнений решаемой задачи создавалась искусственно возведением вычисленных невязок в степень p = 1,1.

Результаты расчетов представлены на рисунке 2, а – г . Для всех четырех рассмотренных случаев полученное решение с пренебрежимо малой погрешностью совпадает с точным решением задачи.

Следующей, уже «физической» задачей, на которой проводилось тестирование итерационного драйвера, являлась задача конвекции в квадратной полости при нагреве сбоку. В этом случае проводилось сравнение с данными из [7]. Значения максимумов функции тока для числа Pr = 1 и различных значений чисела Gr, полученные на сетке 15 х 15 узлов, представлены в таблице 1. Небольшое отклонение (в пределах1-2%) результатов настоящей работы от данных из [7] объяснимо имеющимися различиями в используемых вычислительных схемах.

1.5

0.5

y

-0.5

-1

1.5

0.5

y

-0.5

-1

-1.5

-1

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

-1

-0.5

0.5

1.5

x

-1.5

-1.5

1.5

0.5

y

-0.5

-1

1.5

0.5

y

-0.5

-1

-1.5

-1

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

0.8

0.6

0.4

0.2

-0.2

-0.4

-0.6

-0.8

-1

-1

-0.5

0.5

1.5

x

-1.5

-1.5

в

г

Рис. 2 . Полученные решения уравнения Лапласа на круге для m = 1 ( a ); m = 2 ( б); m = 3 ( в ); m = 4 ( г )

Дополнительно проводилось сравнение значений максимума функции тока и интегрального теплового потока Nu на правой стенке для чисел Gr = 10000 и Pr = 1 с данными из [8]. Значения, полученные в настоящей работе на четырех различных сетках, представлены в таблице 2. В последней строке таблицы приведены предельные значения, полученные в [8].

Таблица 1. Значения максимумов функции тока для различных Gr и Pr = 1

Gr	V max (настоящая работа)	V max [7]
200	0,263	0,258
2000	2,34	2,30
20000	9,05	8,94
200000	16,72	16,63

Таблица 2. Значения максимума функции тока и интегрального теплового потока на правой стенке для Gr = 10000 и Pr = 1

Сетка	V max	Nu
10 X 10	6,9035	1,8934
20 X 20	6,4957	1,7466
50 X 50	6,3857	1,7378
100 X 100	6,3707	1,7432
[8]	6,37	1,752

На решении этой же задачи протестированы механизмы итерационного драйвера по расщеплению итерационного процесса на подпроцессы и перенумерации переменных.

• 5.    Производительность

Применение итерационного драйвера может весьма негативно сказываться на производительности расчетной программы. За потери производительности ответственны, главным образом, процедуры, предоставляющие доступ к элементу объекта-решения по «паспорту» точки вычислительного домена.

Суммарное время такого доступа составляют внутренние временные затраты итерационного драйвера и внешние затраты на вызов процедуры преобразования «паспорта» точки вычислительного домена в номер соответствующей переменной решаемой задачи. Грамотная оптимизация написанного кода поможет снизить внутренние потери производительности. Что касается внешних потерь, то здесь, в некоторых случаях, может оказаться полезным механизм кэширования преобразования «паспорта» в «номер», включенный в драйвер.

Кэширование производится на основе хэш-таблицы, заполняемой парами «паспорт — номер» во время работы итерационного драйвера. Драйвер позволяет подключать стороннюю процедуру кэширования, что необходимо, если «паспорт» точки вычислительного домена модифицируется (стандартная процедура работает только со стандартным «паспортом»).

К сожалению, для простых задач, рассмотренных в настоящей работе, не удается продемонстрировать эффект использования механизма кэширования, так как внешние временные затраты на преобразование «паспорта» точки вычислительного домена в номер соответствующей переменной весьма сильно маскируются внутренними затратами. Применение данного механизма имеет смысл в том случае, когда указанное преобразование требует достаточно сложного алгоритма.

Для небольших задач потери производительности могут оправдываться сокращением времени разработки расчетной программы. С ростом же размера и сложности решаемой задачи трудноустранимые затраты времени в линейном решателе имеют тенденцию к превышению всех прочих потерь производительности.

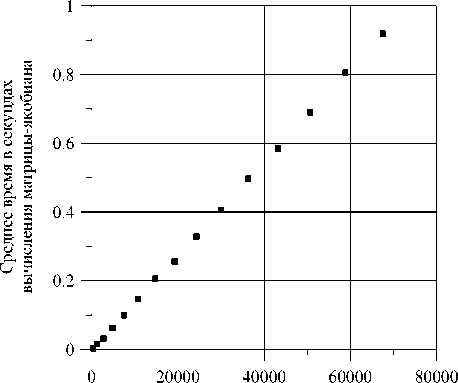
Означенная тенденция проиллюстрирована на рисунке 3, а – г для задачи конвекции в квадратной полости при нагреве сбоку для чисел Gr = 2000 и Pr = 1 . Расчет производительности производился на компьютере со следующими характеристиками: Intel® Pentium® D930 (3.0GHz, 2MB L2 Cache, 800MHz FSB, EM64T, Hyper-Threading) — Memory 512Mb DDR2 SDRAM (2*256Mb) 533MHz — Disk 160Gb (7200 tmp) SATA DataBurst Cache™. Расчеты производились на ряде квадратных сеток, продольный размер которых находился в диапазоне от десяти до ста пятидесяти узлов включительно.

Как видно из рисунка 3, а , средние затраты времени на вычисление матрицы-якобиана растут линейно с ростом числа переменных решаемой задачи. Очевидно, что данные затраты пропорциональны, с зависящим от задачи коэффициентом, среднему времени доступа к элементу объекта-решения и числу таких элементов. Оцененное время

Число переменных

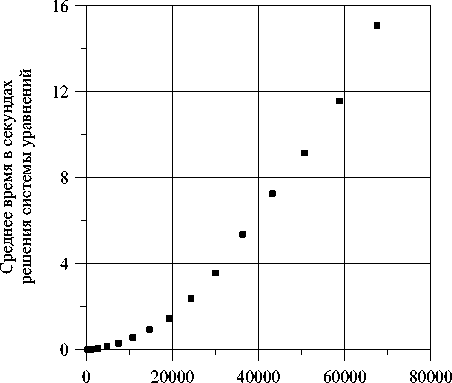
Число переменных б

Число переменных

Продольный размер квадратной сетки

в                                                  г

Рис. 3. Зависимости затрат времени на вычисление матриц-якобианов и решение систем уравнений от числа переменных задачи (продольного размера квадратной сетки)

доступа оказалось неожиданно большим — порядка одной десятой микросекунды, что объясняется значительным количеством вызовов разных вспомогательных процедур внутри процедуры вычисления матрицы-якобиана. Данный факт указывает на то, что вопрос оптимизации разработанного кода требует пристального внимания.

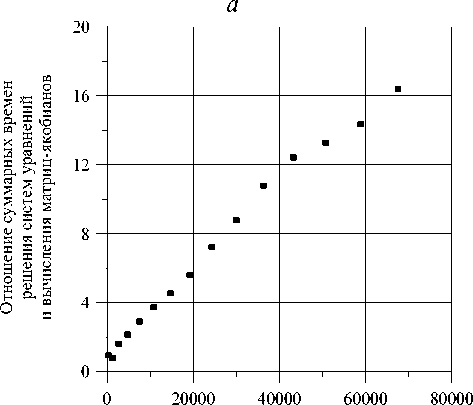
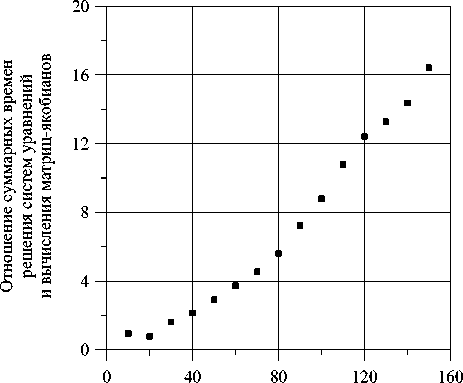
Применение неявной схемы к дискретизации уравнений решаемой задачи обуславливает неплохую заполненность матриц-якобианов (по сравнению с выбором явной схемы) и, как следствие, нелинейный рост потерь производительности в линейном решателе с ростом числа переменных (Рис. 3, б).

Отношение затрат времени в линейном решателе к затратам на вычисление матриц-якобианов демонстрирует заметный рост по мере увеличения числа переменных решаемой задачи (Рис. 3, в, г ). Видно, что уже на сетке небольшого размера (20 х 20 узлов) рассматриваемое отношение оказывается порядка единицы, достигая значения порядка десяти на сетке 100 х 100 узлов, и продолжает расти далее.

Из всего вышесказанного следует, что использование итерационного драйвера не приводит к каким-либо существенным потерям производительности в задачах, для решения которых требуется итерационный метод Ньютона и неявная схема дискретизации определяющих соотношений.

Работа выполнена при финансовой поддержке Министерства образования РФ и Американского фонда гражданских исследований и развития (CRDF) в рамках программы «Фундаментальные исследования и высшее образование» (BRHE) (проект Y5-P-09-03).