Разработка бизнес-приложения для обработки и анализа данных по финансовым рынкам с помощью языка R

Исследование данных является одной из наиболее актуальных проблем современности. Это связано с тем, что объемы обрабатываемой в настоящее время информации колоссальны и продолжают расти. Поиск закономерностей, прогнозирование и модели-

Букунов С.В., Букунова О.В. Разработка бизнес-приложения...

рование находят свое применение в самых разных областях: экономике, медицине, физике и т.д.

В последние годы одним из популярных средств для обработки и визуализации данных в области больших данных (Big Data), науки о данных (Data Science) и машинного обучения (Machine Learning) стал язык R [3; 4; 9; 12; 13]. Он постоянно находится в верхних строчках рейтингов наиболее используемых в этих сферах деятельности языков. Так, например, портал KDnuggets ежегодно проводит опрос среди читателей, желая выяснить, какие инструменты программирования используют специалисты в той или иной области. На рисунке 1 представлено распределение голосов более 1800 опрошенных пользователей программного обеспечения (ПО) в сфере аналитики, науки о данных и машинного обучения в 2017–2019 гг. [15].

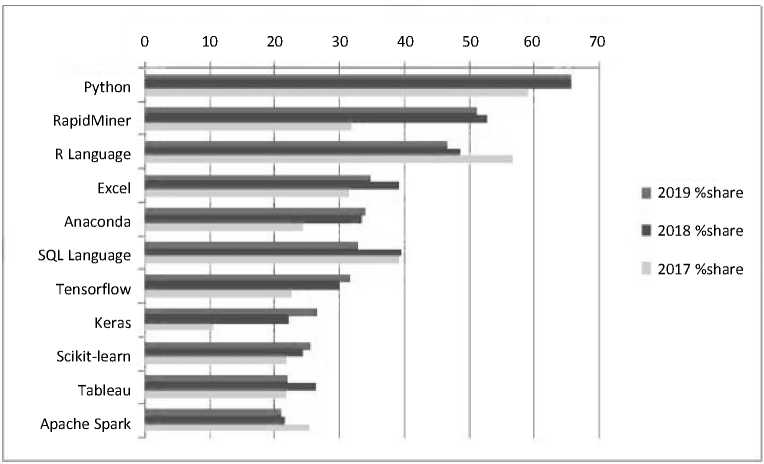
Рис. 1. Рейтинг популярности ПО для обработки данных портала KDnuggets

Из рисунка 1 видно, что, несмотря на снижение относительно пика своей популярности в 2017 г., язык R по-прежнему занимает в данном рейтинге почетное третье место, при этом темпы снижения популярности в 2019 г. существенно замедлились (–4% в 2019 г. против –14% в 2018 г.) [15]. Согласно опросу, в своей работе с данными в 2019 г. язык R использовали 46,6% пользователей.

Следует отметить, что представленный на рисунке 1 рейтинг составлен для сред разработки, а не для языков программирования. Присутствие в этом рейтинге таких языков, как Python, R, SQL, обусловлено тем, что эти языки объединяют язык программирования и среду разработки.

В таблице представлен рейтинг популярности языков программирования, составленный еще одним авторитетным порталом PYPL по результатам 2019 г. [14].

184 в ыпуск 1/2020

Рейтинг популярности языков программирования портала PYPL, %

Место	Язык	Популярность	Изменение за 12 мес.
1	Python	29,49	+4,5
2	Java	19,57	–2,4
3	Javascript	8,4	+0,1
4	C#	7,35	–0,4
5	PHP	6,34	–1,2
6	C/C++	5,87	–0,4
7	R	3,82	–0,2
8	Objective-C	2,6	–0,7
9	Swift	2,57	–0,1
10	Matlab	1,87	–0,2
11	TypeScript	1,87	+0,3
12	Kotlin	1,61	+0,6
13	Ruby	1,47	–0,1
14	VBA	1,39	–0,1
15	Go	1,25	+0,3
16	Scala	1,15	–0,1
17	Visual Basic	0,99	–0,2
18	Rust	0,64	+0,3
19	Perl	0,57	–0,1
20	Lua	0,37	–0,0
21	Haskell	0,29	–0,0
22	Julia	0,28	+0,0
23	Delphi	0,25	+0,0

Индекс PYPL (PopularitY of Programming Language Index) показывает, насколько популярен язык программирования среди тех, кто еще учится. Индекс считается по поисковым запросам обучающих материалов в поисковой системе Google. Согласно представленным данным интерес к языку R как к языку программирования тоже достаточно высок.

Причины высокой популярности языка R:

• •    R объединяет в себе язык программирования и среду разработки [9];

• •    R представляет собой функциональный язык программирования с большим количеством встроенных функций и относительно простым синтаксисом (по сути, R – это набор команд) [4];

• •    R представляет собой бесплатное программное обеспечение с открытым исходным кодом, что позволяет любому пользователю расширять функциональные возможности языка;

• •    R присуща неимоверная гибкость за счет огромного количества подключаемых библиотек, что позволяет создавать приложения для решения практически любой прикладной задачи.

Недостатки языка R вытекают из его же достоинств. В первую очередь это большое количество функций, запомнить которые невозможно и вводить которые нужно вручную.

Букунов С.В., Букунова О.В. Разработка бизнес-приложения...    185

Краткий обзор существующих решений

В настоящее время модули по обработке и анализу данных по котировкам финансовых активов встроены в большинство торгово-аналитических систем, используемых для работы на финансовых рынках [2]. Среди наиболее популярных платформ можно выделить следующие:

• •    MetaTrader 5 – продукт компании MetaQuotes Software Corp. [8];

• •    Quik – продукт компании ARQA Technologies [5];

• •    Transaq – продукт компании «Скрин маркет системз» [6].

Системы такого уровня предлагают пользователю развернутый инструментарий для проведения аналитических исследований в виде библиотек стандартных индикаторов и осцилляторов технического анализа, а также средства для разработки собственных индикаторов. Для этих целей и для автоматизации процесса торговли с помощью собственных алгоритмов (торговых роботов) такие платформы содержат один или несколько языков программирования, в частности:

• •    достаточно полноценный встроенный объектно-ориентированный язык программирования MQL5 (платформа MetaTrader 5);

• •    встроенный язык программирования ATF (платформа Transaq);

• •    встроенный язык программирования Qpile, а также стандартный язык программирования Lua (платформа Quik).

Кроме того, некоторые платформы, например MetaTrader 5, предлагают пользователям готовых торговых роботов. Однако все они представляют собой «черный ящик», внутрь которого заложен некоторый (неизвестный конечному пользователю) алгоритм. Программы типа «черный ящик» говорят, что и когда надо покупать или продавать, не объясняя, почему нужно это делать. Как правило, к таким программам обязательно прилагается солидный «послужной список», впечатляющий биржевыми достижениями. Но правда жизни заключается в том, что финансовые рынки все время меняются и «черный ящик» бессилен перед этими изменениями. Не помогают даже системы со встроенной оптимизацией, поскольку неизвестно, какая именно оптимизация потребуется в будущем. Поэтому в условиях постоянно изменяющихся рынков прибыльная торговля с помощью «черных ящиков», как правило, оказывается очень недолговечной.

К недостаткам торговых платформ следует также отнести отсутствие возможностей для проведения полноценного анализа взаимосвязей между различными финансовыми активами (корреляционного анализа, регрессионного анализа и т.д.), а также инструментария для эффективного управления портфелем финансовых активов.

Наконец, для использования возможностей любой торговой платформы необходимо открытие брокерского счета в брокерской компании.

В данной работе предпринята попытка создания на базе функциональных возможностей языка R информационно-аналитического модуля, позволяющего проводить технический анализ и статистическую обработку данных по котировкам как произвольного финансового актива, так и группы финансовых активов, используя данные из открытых источников и не прибегая к услугам брокера.

Источник данных

В качестве источника данных по ценам на финансовые активы в работе использовался портал финансового холдинга «ФИНАМ» [10]. Данный ресурс позволяет получать

186 в ыпуск 1/2020

историю по котировкам всех финансовых активов, торгующихся на Московской бирже, за любой период времени. При этом данные можно сохранять или в текстовом файле (файл с расширением .txt), или в csv-файле (файл с расширением .csv). Фрагмент такого файла с котировками цен на акции ПАО «Газпром» приведен на рисунке 2. В файле, в частности, содержится информация о наименовании ценной бумаги (поле TICKER), рассматриваемом периоде времени (поле PER, в данном случае это один день), ценах открытия и закрытия (поля OPEN и CLOSE), максимальной и минимальной ценах (поля HIGH и LOW), а также об объемах совершенных сделок по данной ценной бумаге (поле VOL).

\ GAZP — Блокнот

Файл Правка Формат Вид Справка

;;;;;;;;|
GAZP;D	20180110;000000;140.4900000	143.4300000;139.5800000	143.4300000	51756440
GAZP;D	20180111;000000;143.2300000	144.8000000;142.3100000	144.5800000	38571480
GAZP;D	20180112;000000;144.2100000	144.5400000;141.6400000	143.9900000	36760620
GAZP;D	20180115;000000;144.ЗЗООООО	145.5000000;142.6000000	142.9900000	30037050
GAZP;D	20180116;000000;143.1600000	145.3500000;141.8900000	145.2900000	36982660
GAZP;D	20180117;000000;144.5100000	149.2000000;143.3100000	148.7000000	64088350
GAZP;D	20180118;000000;148.7900000	150.3500000;148.1300000	150.3500000	53857120
GAZP;D	20180119;000000;149.9400000	151.0000000;148.4000000	149.1300000	38996740
GAZP;D	20180122;000000;149.0900000	150.3000000;148.8500000	150.3000000	22745110
GAZP;D	20180123;000000;150.8000000	151.6500000;147.7100000	148.8000000	35760870
GAZP;D	20180124;000000;148.5100000	149.7000000;146.6000000	149.7000000	24826570
GAZP;D	20180125;000000;150.0200000	151.3900000;149.2700000	149.8000000	41825580
GAZP;D	20180126;000000;149.4000000	149.5500000;146.0100000	147.1900000	35266440
GAZP;D	20180129;000000;146.7700000	147.2900000;144.1500000	144.7500000	36073370
GAZP;D	20180130;000000;144.0000000	146.4300000;142.3700000	143.5000000	50304710

Рис. 2. Фрагмент файла, экспортированного с портала холдинга «ФИНАМ»

Язык R поддерживает операции импорта/экспорта этих типов файлов, поэтому полученные таким образом данные могут быть легко импортированы в R для дальнейшей обработки. Количество записей в файлах зависит от рассматриваемого периода времени и, как правило, составляет десятки и сотни тысяч для одного эмитента. При этом при проведении статистического анализа одновременно могут использоваться данные по нескольким десяткам эмитентов. Очевидно, что обрабатывать такие объемы данных средствами популярных электронных таблиц (например, Microsoft Excel) крайне неудобно. Язык R, напротив, предлагает обширный инструментарий для обработки таблиц большого размера.

Основные функциональные возможности приложения

Для работы с приложением были созданы текстовые файлы, содержащие данные по биржевым котировкам наиболее ликвидных ценных бумаг (акций российских компаний), а также котировкам производных финансовых инструментов (фьючерсных контрактов на ценные бумаги, биржевые товары (нефть, драгоценные металлы и др.) и валюты) за последние двадцать лет. Для каждого финансового инструмента были собраны данные за разные интервалы времени, а именно: пять минут, пятнадцать минут, полчаса, один час, один день, одна неделя и один месяц.

Для проведения технического анализа выбранного актива были реализованы функции по расчету наиболее популярных индикаторов технического анализа, таких как, например, простые и экспоненциальные скользящие средние, осциллятор импульса (Momen-

Букунов С.В., Букунова О.В. Разработка бизнес-приложения...    187

tum), процентный интервал Уильямса (Williams %R), стохастический осциллятор и др. [11]. Примеры расчета некоторых используемых индикаторов приведены ниже.

Для проведения статистической обработки данных пользователь может выбрать необходимый статистический показатель и тип графической визуализации (например, тот или иной вид корреляционной матрицы или диаграммы рассеяния). Для визуализации результатов используются как встроенные возможности языка R, так и возможности некоторых внешних библиотек, таких как, например, ggplot2 и ellipse .

Работа с приложением осуществляется с помощью простого графического интерфейса, позволяющего пользователю выбрать необходимый финансовый инструмент (или группу инструментов), анализируемый период времени, необходимый масштаб времени, индикатор технического анализа (или группу индикаторов), статистический показатель (или группу показателей), вид графической визуализации. Для создания графического интерфейса в работе использовалась библиотека rpanel .

Расчет экспоненциальных скользящих средних

Экспоненциальные скользящие средние традиционно относятся к одним из наиболее популярных трендовых индикаторов классического технического анализа. Этот индикатор встроен в практически все современные торговые терминалы, предоставляющие доступ к электронным биржевым торгам. На нем основано подавляющее количество так называемых трендовых торговых стратегий [1; 7]. Все трендовые модели содержат в своей основе различные усредненные параметры, главный смысл которых заключается в фильтрации случайных ценовых колебаний.

Для расчета значений экспоненциальной скользящей средней (Exponential Moving Average, EMA) n -го порядка в каждый момент времени использовалась итерационная формула

EMA( i ,n ) = kP, + ( 1 - k ) EMA ( i - 1, n ) ,                       (1)

где EMA( i, n ) – экспоненциальная скользящая средняя в текущий момент времени i (например, в данный день); k – коэффициент сглаживания, рассчитываемый по формуле ²

k =----; P, - цена в текущий момент времени i; n - порядок средней (количество рас- n +1

сматриваемых временных периодов, в данном случае количество дней); EMA( i – 1, n ) – экспоненциальная скользящая средняя в предыдущий момент времени i – 1 (например, в предыдущий день).

В качестве значения EMA( i – 1, n ) для первой точки используется простая скользящая средняя (Single Moving Average, SMA) SMA( i – 1, n ) нужного порядка.

Расчет процентного интервала Уильямса (Williams %R)

Процентный интервал Уильямса (Williams %R) представляет собой простой, но очень действенный индикатор. Этот осциллятор позволяет оценить способность покупателей или продавцов закрыть цены у границы недавнего ценового диапазона. Индикатор %R подтверждает наличие тенденций и предупреждает о возможных разворотах:

, ,   P - H

% R ( i , n ) =  ----- 100%,                          (2)

Hn - Ln где Pi – текущая цена закрытия; Hn – максимальная цена за последние n периодов; Ln – минимальная цена за последние n периодов.

188 в ыпуск 1/2020

Индикатор %R определяет положение текущей цены закрытия относительно недавнего диапазона между максимумами и минимумами.

Расчет стохастического осциллятора (%K и %D)

Стохастический осциллятор (или стохастик) измеряет соотношение между каждой из цен закрытия и недавним диапазоном максимумов и минимумов. Он несколько сложнее осциллятора %R, поскольку его расчет производится в несколько этапов, на каждом из которых отсеивается рыночный шум и отбраковываются ложные сигналы. Стохастический осциллятор состоит из двух линий: быстрой (%K) и медленной (%D).

Расчет стохастика производится по следующему алгоритму.

На первом этапе рассчитывается несглаженная стохастическая линия:

P - L„

% K ( i, n ) = —----100%.

H n - L n

На втором этапе рассчитывается сглаженная линия %D, которая представляет собой линию %K, сглаженную с помощью простой скользящей средней (по умолчанию трехпе-

риодной, т.е. m = 3):

,   , SMA( P - L , m )

% D( i, m ) =-----— 100%.

SMA( H„ - L , m )

По умолчанию значение для периода n = 14, но пользователь может задать любое произвольное число.

Расчет статистических показателей

Язык R предоставляет развернутый инструментарий для проведения статистического анализа. В данной работе для расчета статистических показателей, таких как, например, дисперсия, межквартильный разброс, коэффициент корреляции и другое, использовались стандартные встроенные функции R, в частности функции sd() , IQR() , cor() и др.

Для построения корреляционных матриц различного вида использовались как встроенные функции R, так и некоторые внешние библиотеки, в частности библиотека ellipse .

Результаты

Ниже приведены некоторые результаты работы приложения.

На рисунке 3 представлены результаты визуализации динамики дневных цен закрытия (т.е. период изменения цены – один день) на акции ПАО «Роснефть» за 2009 г., полученные с помощью стандартной встроенной функции plot() . Дополнительно построены графики (см. рис. 3) трех экспоненциальных скользящих средних с разными значениями периода усреднения, а именно: 13, 21 и 28 дней – и график изменения объемов сделок.

Для визуализации данных, содержащих так называемые выбросы, в R предназначен такой тип графиков, как диаграммы размаха. В настоящей работе реализована возможность построения двух видов подобных диаграмм: бокс-плоты и скрипичные диаграммы.

Бокс-плоты (от англ. box plot – «ящик с усами») снискали популярность у исследователей данных благодаря высокой наглядности, поскольку они позволяют очень полно представить на одном графике сводную статистическую информацию одновременно для нескольких групп данных, выделенных в соответствии с уровнями той или иной категориальной переменной. Для каждой группы данных отображаются медиана, нижний

Букунов С.В., Букунова О.В. Разработка бизнес-приложения...    189

и верхний квартили, интервал («усы»), в который попадает подавляющее большинство наблюдений, а также наблюдения-выбросы, оказавшиеся за пределами этого интервала.

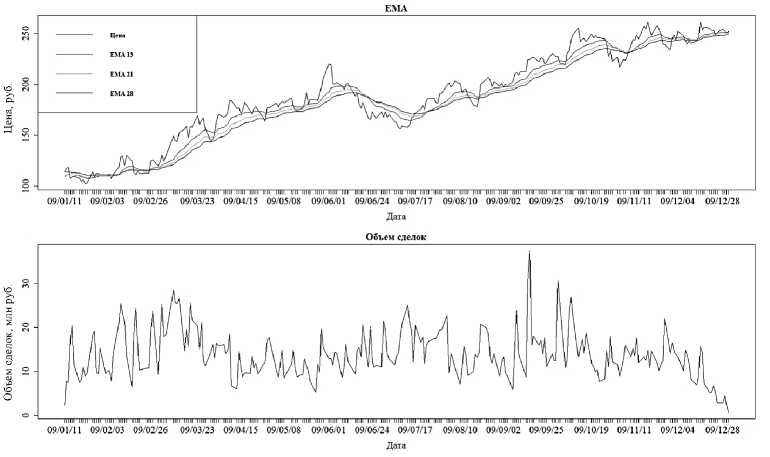
09/01/11 09/02/03 09/02/26 09/03/23 09/04/15 09/05/08 09/06/01 09/06/24 09/07/17 09/08/10 09/09/02 09/09/25 09/10/19 09/11/11 09/12/04 09/12/28

Рис. 3. Визуализация динамики цен и объемов сделок с акциями ПАО «Роснефть» за 2009 г. с помощью встроенной функции plot()

На рисунке 4 приведены результаты моделирования разброса (волатильности) цен на различные финансовые активы за 2015 г., полученные с помощью функции geom_box-plot() из библиотеки ggplot2 . Набор данных состоит из акций компаний различных секторов экономики, нескольких наиболее популярных валют и индекса Московской межбанковской валютной биржи (ММВБ). Для удобства проведения сравнительного анализа цены на диаграмме отображаются в относительных единицах (от 0 до 1).

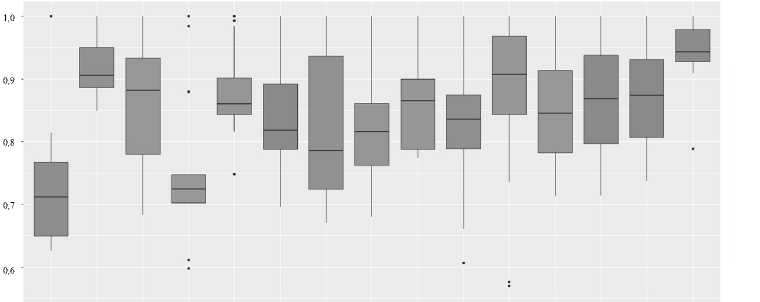
Транснефть Газпром Новатэк Сбербанк ВТБ ГМКНорНикель ВСМПО НЛМЛ РусГидро ФСК ИнтерРАО Доллар США Евро Фунт стерлингов Индекс ММВБ ЦБ

Рис. 4. Визуализация разброса цен с помощью функции geom_boxplot()

190 в ыпуск 1/2020

Для построения диаграмм размаха на рисунке 5 используется функция geom_violin() из библиотеки ggplot2 , которая позволяет строить так называемые скрипичные диаграммы. Скрипичные диаграммы дают возможность сделать диаграммы размаха более информативными, поскольку они объединяют идеи диаграмм размаха и кривых плотности вероятности. Основная идея этих диаграмм достаточно проста: продольные края «ящиков» на диаграмме размаха заменяются кривыми плотности вероятности. В итоге получаются симметричные фигуры, чьи очертания напоминают очертания скрипки – отсюда и название этого типа диаграмм.

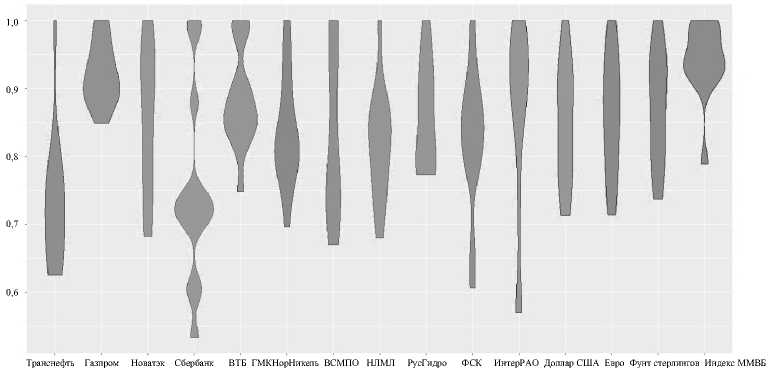
ЦБ

Рис. 5. Визуализация разброса цен с помощью функции geom_violin()

Вывод численных значений выбранных статистических показателей для выбранного финансового актива выглядит следующим образом:

• [1]    «Статистика для цены акции НЛМК»:

• [1]    «Стандартная вариация: 5.31838763577223»

• [1]    «Дисперсия: 28.285247044335»

• [1]    «Межквартильный разброс: 5.39»

• [1]    «Коэффициент вариации: 28.285247044335»

Язык R предоставляет развернутый инструментарий для проведения корреляционного анализа. Для вычисления коэффициента корреляции в R используется функция cor() . В простейшем случае ей передаются два аргумента (векторы одинаковой длины). Однако возможен вызов этой функции и с одним аргументом, если этим аргументом является матрица или таблица данных. В последнем случае функция cor() вычисляет так называемую корреляционную матрицу, составленную из коэффициентов корреляций между столбцами матрицы или набора данных, взятых попарно.

В качестве примера проведения простого корреляционного анализа средствами R на рисунке 6 представлены результаты корреляционного анализа цен на нефть (долл./бар-рель) и золото (долл./унция) за 2017 г., выполненные с помощью функции cor() . Для оценки взаимосвязи между ценами на выбранные активы были построены диаграмма рас-

Букунов С.В., Букунова О.В. Разработка бизнес-приложения...

сеяния (коррелограмма), линия регрессии, а также линии отклонения от нее на величину ошибки (±1 RMSE).

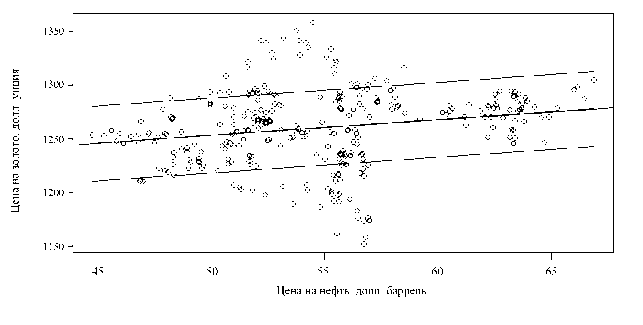
Рис. 6. Коррелограмма цен на нефть и золото в 2017 г.

Для численного значения коэффициента корреляции был получен следующий результат:

• [1]    «Коэффициент корреляции между ценами на нефть и золото: 0.199015894209241»

• [1]    «С большой вероятностью связь между ценами отсутствует»

Приложение предоставляет пользователю различные варианты построения корреляционных матриц, а именно:

• •    обычные матрицы, содержащие коэффициенты корреляции в числовом виде (встроенные функции cor() , symnum() );

• •    корреляционные матрицы в графическом виде (встроенная функция image() , функция plotcorr() из пакета ellipse ).

Фрагмент результата вычисления корреляционной матрицы с помощью встроенной функции cor() для набора данных, используемых для построения диаграмм размаха на рисунках 4–5, представлен на рисунке 7.

	Транснефть	Газпром	Новатэк	Сбербанк	ВТБ	ГМКНорНикель	ВСМПО	НЛМЛБ
Транснефть	1.000000000	-0.20956868	0.62381158	0.68055464	0.40308456	0.001502119	0.80814406	-0.20205431
Газпром	-0.209568675	-.00000000	-0.01964365	-0.07042017	-0.12190562	0.627530898	-0.16237029	0.34857490
Новатэк	0.623811583	-0.01964365	1.00000000	0.70838030	0.45947546	-0.174431859	0.73276721	-0.12757882
Сбербанк	0.680554637	-0.07042017	0.70838030	1.00000000	0.43785245	-0.230091927	0.65654238	-0.41250941
ВТБ	0.403084556	-0.12190562	0.45947546	0.43785245	1.00000000	-0.332049057	0.13018713	-0.26382814
ГМКНорНикель	0.001502119	0.62753090	-0.17443186	-0.23009193	-0.33204906	1.000000000	0.10424562	0.81953598
ВСМПО	0.808144063	-0.16237029	0.73276721	0.65654238	0.13018713	0.104245618	1.00000000	-0.01935665
НЛМЛ	-0.202054314	0.34857490	-0.12757882	-0.41250941	-0.26382814	0.819535982	-0.01935665	1.00000000
РусГидро	0.526392638	-0.07930128	0.36057369	0.77111672	0.35396786	-0.182534733	0.49482935	-0.44153696
ФСК	-0.133640541	0.68548881	0.22983627	0.25874742	-0.02479637	0.283317829	-0.04841294	0.04040920
ИнтерРАО	0.073510488	0.16222430	0.57200109	0.54709433	0.38027102	-0.260265386	0.19168528	-0.30747960
Доллар США	0.859196748	-0.25755864	0.45163724	0.47074810	0.08160777	0.277132003	0.82669243	0.17995274
Евро	0.786136186	-0.3-531698	0.31617546	0.26246581	0.01583782	0.240819440	0.73820705	0.18358165
Фунт стерлингов	0.855177291	-0.22578418	0.50219022	0.44737894	0.11393348	0.272511638	0.82279779	0.21396811
Индекс ММВБ	0.543695273	0.48442673	0.61857787	0.74524096	0.20306599	0.419548469	0.59481436	0.13402164

Рис. 7. Фрагмент корреляционной матрицы, рассчитанной с помощью функции cor()

Когда корреляционная матрица достаточно велика (даже в данном случае на рисунке 7 изображен только фрагмент матрицы), воспринимать и анализировать ее становится сложно. В этих случаях приложение позволяет пользователю вывести корреляционную

192 в ыпуск 1/2020

матрицу, в которой числовые значения коэффициентов корреляции заменяются символами, каждый из которых соответствует одному из числовых диапазонов, в который попадает данное числовое значение. Такую матрицу можно построить с помощью встроенной функции symnum() . Результат применения функции symnum() к используемому выше набору данных показан на рисунке 8.

На

С

ГМ

ВС

нм

р

ФС

Ине

Д

Е

Фу Инд

Транснефть Газпром Новатэк Сбербанк ВТБ ГМКНорНикель ВСМПО НЛМК

ФСК

ИнтерРАО

Доллар. США

Фунт.стерлингов

Инде кс. ММВБ atti (,"legend")

В в

в

. 1

[1] о

0.3

О. б

0.3

0.9

0.95

В1

Рис. 8. Корреляционная матрица, рассчитанная с помощью функции symnum()

Еще одним способом визуализации корреляционных матриц большого размера является представление коэффициентов корреляции в графическом виде. Для графического отображения корреляционных матриц в данной работе предусмотрено два варианта.

Первый вариант заключается в визуализации корреляционной матрицы в виде так называемой «тепловой карты» (heatmap). В этом случае каждому диапазону значений коэффициента корреляции назначается свой цвет.

Такую матрицу можно получить с помощью встроенной функции image() . Результат применения этой функции к используемому выше набору данных показан на рисунке 9.

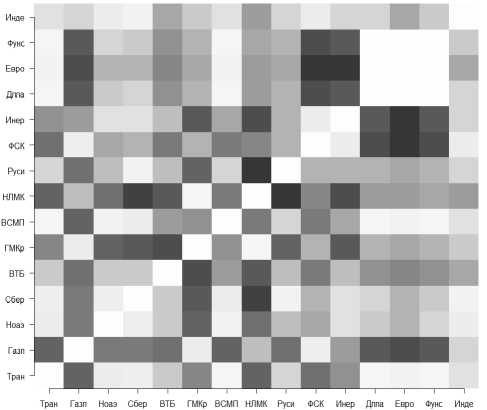
Букунов С.В., Букунова О.В. Разработка бизнес-приложения... 193

В данном случае темно-серый цвет соответствует отрицательной корреляции (коэффициент корреляции –1), белый цвет – положительной корреляции (коэффициент корреляции +1), а различные оттенки серого – промежуточным значениям коэффициента корреляции.

Вторым способом визуализации корреляционной матрицы является использование функции plotcorr() из пакета ellipse . В этом случае числовые значения коэффициента корреляции изображаются в виде эллипсов, форма которых зависит от значения коэффициента корреляции: чем оно ближе к –1 или +1, тем более вытянутым становится эллипс. Наклон эллипса определяется знаком коэффициента корреляции. Результат применения этой функции к используемому выше набору данных показан на рисунке 10.

Газпром

Новатэк

Сбербанк

ВТБ ешее

ГМКНорНикель 0^000