Разработка и анализ однопродуктовых динамических моделей формирования оптимальной производственной программы в условиях детерминированного описания среды

Основным процессом производственного планирования на тактическом уровне является формирование производственной программы, отражающей ассортимент и объемы продукции, подлежащей выпуску в плановом периоде, с учетом имеющихся резервов и возможностей предприятия.

В процессе формирования программы должны учитываться действующие и планируемые производственные мощности, потребности в материалах, стратегии потенциальных поставщиков в отношении цен и объемов производства, стратегии снабжения и т.д. При этом производственная программа является интегрирующим, связующим этапом в планировании, на этом этапе от принятых решений напрямую зависят следование общей стратегии предприятия, прибыль, ассортимент выпускаемой продукции. Формирование производственной программы является сложным процессом, требующим комплексного подхода. В связи с особенностями маркетинговой программы, имеющихся ресурсов, потребностей в ресурсах может быть множество производственных программ, эффективность при реализации которых будет разной. Поэтому становится актуальной задача выбора наиболее оптимальной программы по некоторому критерию, определяемому исходя из цели и общей стратегии предприятия.

Сформированная оптимальная производственная программа предприятия служит необходимой информационной основой для решения задач в других разделах бизнес-плана, в частности финансового плана [8]. Наиболее удобным и эффективным методом поиска оптимальной производственной программы является моделирование, что дает возможность проигрывания различных сценариев при изменении параметров объекта, анализе различных стратегий и выборе наилучшей.

Исследования в области формирования оптимальной производственной программы

начались в 30-х гг. с работ Л.В. Канторовича, который впервые предложил математическую постановку производственных задач оптимального планирования и эффективные методы их решения, приемы их экономического анализа. Дальнейшее развитие и обобщение теория оптимального планирования и управления производством на основе экономико-математических методов получила в работах А.А. Первозванского, А.В. Пархоменко, Б.И. Герасимова, А.В. Мищенко и др.

В работе А.А. Первозванского «Математические модели в управлении производством» [3] разработаны различные типы моделей формирования производственной программы. Построенные модели не позволяют получить оптимальную программу производства при сезонности спроса в связи с накоплением к концу периода планирования нереализованных остатков либо при нехватке готовой продукции для удовлетворения спроса. Это приводит к росту издержек, нерациональному производству и вследствие этого к снижению эффективности производства.

В работах А.В. Архипова, Р.А. Файзрахманова, А.П. Косякова исследованы проблемы моделирования и управления материальными потоками в производственных системах, построены и проанализированы комплексные модели планирования производства и управления запасами. Модели построены с учетом одной стратегии - закупки сырья партиями оптимального объема и без учета возможности производства дополнительного объема продукции в ранние периоды с целью удовлетворения спроса в более поздние периоды, когда производственных мощностей недостаточно [6]. Но именно проработка этих вопросов позволяет создать гибкую и эффективную модель формирования производственной программы.

Т.Г. Шешукова рассматривает понятие и эволюцию коммерческого расчета как одного из методов управления, направленного на обеспечение прибыльности предприятия. Важным принципом коммерческого расчета является соизмерение затрат и результатов, раскрывающих финансовую сторону производственной программы [9].

Среди зарубежных ученых, занимавшихся разработкой положений в области планирования производства на предприятии, можно отметить труды М. Мескона, М. Альберта, Ф. Хедоури, Дж. Стивенсона.

В работе М. Мескона, М. Альберта, Ф. Хедоури [2] рассматриваются и анализируются чистые и смешанные стратегии производства, но не рассматриваются вопросы использования различных стратегий в моделях оптимального планирования производственной программы.

Изучение работ отечественных и зарубежных ученых позволяет сделать вывод, что вопросы построения комплексных моделей производства исследованы недостаточно. Вопрос о производстве дополнительного объема продукции с целью выполнения плана продаж в случае недостаточной мощности при сезонности продаж    в    моделях    формирования производственной       программы       не рассматривается. Учет данного фактора способствует эффективности и обеспечению слаженности    производства,    увеличению прибыли и сокращению производственных затрат.

В данной работе предложены модели формирования оптимальной производственной программы для предприятия, объединяющие процессы производства и закупок с учетом ограничения по производственной мощности, сезонности продаж, издержек от управления запасами. Рассмотрен принцип построения моделей для двух стратегий закупок: периодические закупки и закупки партиями фиксированного объема.

Постановка задачи

Найти оптимальные объемы выпуска продукции x_t , i = 1, n и сырья Л х^ , i = 1, n , максимизирующие прибыль предприятия при следующих данных и предположениях:

• •    предприятие производит по одной технологии продукцию одного вида, для производства которой требуется один вид сырья; продукция и сырье не подвергаются естественной убыли;

• •    продажи производятся в конце каждого месяца;

• •    известны     месячные     значения

ожидаемых продаж d_t , i = 1, n ; месячные номинальные производственные мощности m_t , i = 1, n ;

• •    закупка сырья производится по одной из двух стратегий (стратегия периодических закупок, стратегия закупки фиксированного объема);

• •    известен технологический коэффициент Л , показывающий объем необходимого сырья на единицу готовой продукции; оптовая цена прод

p     продажи единицы продукции; цена зак. с                                                 тМР p    закупки сырья у поставщика; цена p транспортировки, отгрузки единицы сырья поставщиком;

• известны: стоимость C труд труда, затраченного рабочим коллективом на производство единицы продукции; месячная стоимость C с хранения единицы сырья на складе; месячная стоимость гот Сh

хранения

единицы готовой продукции на складе; затраты С^з на выполнение одного заказа у поставщика;

Спз. = n • Сз + pтр. • zj\v ;(4)

i = 1

n ex'" = Ch •Л|^ ;(5)

i=1 V 2

переменные    производственные    затраты

C перем . пр на       единицу       продукции;

C пост

(эксплуатация     оборудования,      аренда помещения, коммунальные расходы и т.д.);

гот остатки готовой продукции z    на начало

xp . г

n С гот .

h • Л

x i ⁺ z

i = 1 V

гот i—1

.

планового периода;

• остатки сырья на начало планового периода считаем равными нулю.

Подставив полученные выражения в целевую функцию прибыли, получим в

окончательном виде:

Построение модели

(n = p ^прд^д ^+ z ^гг^от ye перем ■ ^np + с ^труд )y_Xi

Построим модель в классе задач математического программирования. В качестве целевого функционала рассмотрим прибыль предприятия.     Прибыль     предприятия определяется                  соотношением:

пост     перем

П = TR — C — С , где TR - выручка от реализации продукции за весь период

C пост - постоянные затраты;

С перем

- переменные затраты.

Построение и анализ модели

зак . с .     тр .     ⁿ         з    пост

— \P      + p /• а Л X; — n • С — C      —

'    i = 1 i

C с h

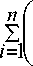
A xi

гот h

n

• Л

xi

+ z

гот i — 1

i = 1

^ max;

произведем при использовании двух основных стратегий закупки: периодических закупок и закупки фиксированного объема. Вопросы о выборе наиболее эффективной стратегии с

точки зрения минимизации затрат исследованы нами в работе [7].

1. Стратегия периодических закупок .

При этой стратегии закупки сырья

x _; >  min( d , m, ) ; x_i <  m_t, i = 1, n ;        (8)

nn zr +Л х<Л dj; J=i         J=i i—1

гот    гот zi   >zо  +Л(xj — dj);

j = 1

.    >  0, i = 1 n ;              (9)

V          x_i >  0, i = 1, n .                 (10)

осуществляются через одинаковые промежутки времени. При построении данной модели будем

Ограничения     (8)

показывают

считать, что закупки происходят раз в месяц.

Определим составляющие прибыли:

TR = pпрод nd-i = 1

проД ( n, ,      . гот ]

- Р    Щ(di - xi) - z0  ) = проД( n

= Р     I Л xi

V i = 1 ¹

гот

+ z 0

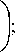
+ С

перем     перем . пр .     труд

С      = I I         + C      г

ⁿ        зак . с .      пз . с .      хр . с .

I • Л Xi + C + С + С i = 1

хр . г .

;

n

C зак . с       зак . с .

= p • а л X i. ;           (3)

i = 1

производство продукции в объемах x не ниже ожидаемых объемов продаж d и не выше производственных      мощностей       m .

Производство продукции в объемах больше d позволяет создать запас для использования его в том случае, когда уровень производства ниже ожидаемых продаж. Ограничения (9) задают схему использования запасов готовой продукции.

• 2.    Стратегия закупки фиксированного объема. При этой стратегии закупки производятся партиями q . Определим составляющие прибыли:

  TR . pпрод nd, - pпрод f £ ( d, i = 1 i             к i = 1 ⁱ

  
  

  - xi )

  
  
  

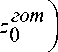
  Уилсона

  
  

  (формула

  
  

  прод f n     гот |

  = P    ^J xi + z 0 J ;

  
  

  2 • С з • ^Г __________________ i = 1 c h • n

  
  

  .

  
  

  EOQ )       [4]:

  
  

С перем _ Г перем. пр + ^рууд ) n^ +         ' i=1x зак.с

При использовании этой формулы модель становится нелинейной. Для сохранения линейности предлагаем формулу

+ С^пз . с

хр . с

+ Сх . ^г ;

n

C зак . с .        зак . с

= P • ^A £ x i ;

i = 1

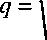
n

2 • С³ • A £ d i

i = 1 c h • n

n

^ £ xi пз.с i=1 i „з , тр.

С ---С + p • A £ x,-(14)

q                         i =1 i

Cp = Chс • qn ;(15)

Исследование и сравнение целевых функционалов в моделях (7) – (10) и (17) – (20)

позволяет получить условие совпадения

моделей и их максимумов:

n nc3 + ch £ i=1

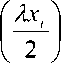
n a£ xi i=1

q

c³ + c_h c qn h ₂

C

xp . г

n

С гот h • £

^{f x}i ⁺ z

гот i-1

n a£ xi

i = 1 к

У

.

^ q =

i = 1

n

При расчете затрат на хранение сырья (15) и готовой продукции (16) использовано

Разница между максимумами моделей будет определяться выражением:

предположение о равномерном расходе запасов сырья и производства готовой продукции [5].

Подставив полученные выражения в

целевую функцию прибыли, получим модель

n nC3 + СУI I-h i=1 к 2 У

n a£ xi

— C

q

-

_С c q_n h ₂

вида:

{ П = p^прод f £ x. к i = 1

гот । пост

^{+ z} 0     I " ^C

^ перем . пр

+ C ^труд )

•

A £ xi n        зак.с. . n       i=1 i „ з

• £ xi - p      • У £ xiС i=1                  i=1

гот тр in    сс q   гоот nx + zi-1 , ,

- p ■ A £ xi - Ci, • ~n - С,    •£ (---------- ) ^ max;

i=1 i   h 2    hi=12

x; > min(d, m;) ; xt < m., i = 1, n ;(18)

Расчеты по формулам (23), (24) позволяют получить количественную оценку разницы в прибыли.

Построенные модели позволяют сформировать оптимальную производственную программу при заданных объемах продаж, значениях производственных мощностей, запасах готовой продукции, затратах, стратегиях закупок с учетом сезонности продаж.

zr + ix < ££dj zr >z0Г +£(x, -d^; j=i         j=ij zr > 0, i = m;(19)

x; > 0, i = 1, n.(20)

Размер партии q может задаваться произвольно, например с учетом политики поставщика. В качестве значения q может

использоваться оптимальное значение. Наиболее известной формулой вычисления оптимального значения q является формула

Пример построения однопродуктовой динамической детерминированной модели производства керамического кирпича

Стратегия периодических закупок

В соответствии с постановкой произведем построение модели при следующих параметрах:

n = 12 мес . ;        z Г = 0 ;        A = 2,5 кг ;

q = 200000 кг ;

Саренда = 1000 кв.м • 320 руб . кв.м • 12 мес . =

= 3 840000 руб . год .;

Сэл.эн = 15 кВт / ч - 240 _ч - 3 руб . кВт / _ч - 12 мес. = = 129600 руб . год.;

_саморт = 1000000руб. . 0,05 = 50000 руб , год .;

f П = 8 • £ x: i = 1 i

12,5 £ xi i = 1

- 4019600-2,605 - £ x_; i = 1 ⁱ

пост   аренда эл . эн аморт

= 3840000 + 129600 + 50000 = 401960С руб . год,

C перемпр = 0,25 кВт / _ч . 3 руб. кВт / ч +

+ 0,0002 куб . м • 25 руб.куб . м. = 0,755 руб.ед .;

^ max;

- 0,03 • 100000-12 - 0,02 • £ i = 1

12 f ^xi ⁺ z

гот z_i

+ £ xj<

j = i

£ d j ;

j = i

_{z i}гот

i - 1

£ (xj j=1

гот i - 1

^- d j )^;

^

C труд = 0,85 руб. C = 0,03 руб .ед. д;

p тр = 0,1 руб.кг.; pпрод = 8руб.ед.;

pзак.с = 0,3 руб. кг.

Подставив    параметры,    получаем следующие модели:

Стратегия периодических закупок:

12                       12

ГП = 8 • Е х. - 4019660 - 2,605 • £ х. - 0,03 • i = 1 i                            i = 1 i гот

12                     12   x. + z.,

£ (1^,25 x ) ^{- 0,02} • £     i i — ¹

i = 1       i           i = 1

\7

^ max;

Проанализируем задачи при различных значениях m по показателям прибыли и ритмичности     производства.     Сравним результаты с вариантом производства по среднему         значению         продаж

• x. = £ d_} /12, i = 1,12 .

• j = 1

Стратегия периодических закупок

Результаты расчетов модели (25) приведены в табл. 1 – 4.

объема:

Стратегия закупки фиксированного

гот zi

12      12

j = i ^j   j = i ^j

z -т >;^ (x , - d , ) ;

J = 1

гот z_i

Таблица 1

Программа производства

x i	y i	d i	mi
119000	297500	114000	119000
119000	297500	115000	119000
119000	297500	117000	119000
119000	297500	120000	119000
119000	297500	122000	119000
119000	297500	123000	119000
119000	297500	124000	119000
119000	297500	123000	119000
119000	297500	120000	119000
119000	297500	118000	119000
119000	297500	118000	119000
119000	297500	118000	119000
Прибыль: 3 592 090 руб.

по среднему значению продаж

График производства, шт.

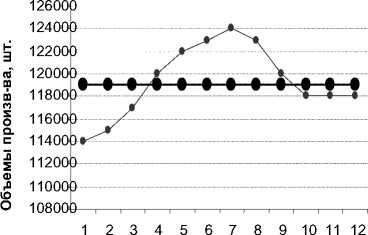
Месяцы

—•— Объем продаж, шт.

Месячная норма выпуска, шт.

—•—Объем производства, шт.

Таблица 2

Программа производства по значениям модели (25)

xi	y i	d i	m i		График производства, шт.
119000	297500	114000	119000
119000	297500	115000	119000		126000 э 124000 я 122000 ш 120000 0 118000 с 116000 1 114000 “ 112000 0 110000			4—4
119000	297500	117000	119000
119000	297500	120000	119000
119000	297500	122000	119000
119000	297500	123000	119000
119000	297500	124000	119000
119000	297500	123000	119000
119000	297500	120000	119000
118000	295000	118000	119000		1    2    3    4    5    6    7    8    9   10  11   12
118000	295000	118000	119000				Месяцы
118000	295000	118000	119000				—•   Объем продаж, шт. .. .>.   Месячная норма выпуска, шт. —•— Объем производства, шт.
Прибыль: 3 600 077,5 руб.

Таблица 3

Программа производства по среднему значению продаж в случае повышения производственной мощности

x i	y i	d i	mi		График производства, шт.
119333	298333	114000	120000
119333	298333	115000	120000		126000 3 124000 го 122000 ш 120000 0 118000 с 116000 I 114000 2 112000 0 110000	1 11  1111 а а 1
119333	298333	117000	120000
119333	298333	120000	120000
119333	298333	122000	120000
119333	298333	123000	120000
119333	298333	124000	120000
119333	298333	123000	120000
119333	298333	120000	120000
119333	298333	118000	120000		1    2   3    4    5    6   7    8    9   10  11   12
119333	298333	118000	120000				Месяцы
119333	298333	118000	120000				—•   Объем продаж, шт. Месячная норма выпуска, шт. —•— Объем производства, шт.
Прибыль: 3 533 383,38 руб.
							—

Таблица 4

Программа производства по значениям модели (25) в случае повышения производственной мощности

xi	y i	d i	mi
118000	295000	114000	120000
120000	300000	115000	120000
120000	300000	117000	120000
120000	300000	120000	120000
120000	300000	122000	120000
120000	300000	123000	120000
120000	300000	124000	120000
120000	300000	123000	120000
120000	300000	120000	120000
118000	295000	118000	120000
118000	295000	118000	120000
118000	295000	118000	120000
Прибыль: 3 637 390 руб.

Анализ результатов показывает, что в первом случае (табл. 1) получаемая предприятием прибыль меньше и к концу периода планирования накапливаются остатки нереализованной продукции.

Анализ и сравнение результатов в табл. 2, 4 позволяет сделать вывод, что за счет увеличения производственных мощностей прибыль увеличилась. С другой стороны, с ростом производственных мощностей увеличивается их недогрузка, что может негативно сказаться на эффективности работы предприятия. По данным табл. 4 (ср. те же данные в табл. 3) выпуск дополнительного объема продукции в первые три месяца происходит ровно в том объеме, который необходим для покрытия дефицита с 5-го по 8-й месяц, что позволяет избежать хранения излишних запасов на складе и увеличить прибыль. При дальнейшем увеличении мощностей тенденция к их недозагрузке и снижению равномерности производства будет расти.

Стратегия закупки фиксированного объема

Результаты расчетов модели (26) приведены в табл. 5 – 7.

Таблица 5

x i	d i	m i
119000	114000	119000
119000	115000	119000
119000	117000	119000
119000	120000	119000
119000	122000	119000
119000	123000	119000
119000	124000	119000
119000	123000	119000
119000	120000	119000
118000	118000	119000
118000	118000	119000
118000	118000	119000
Прибыль: 3 617 485,9 руб.

производства по значениям модели (26)

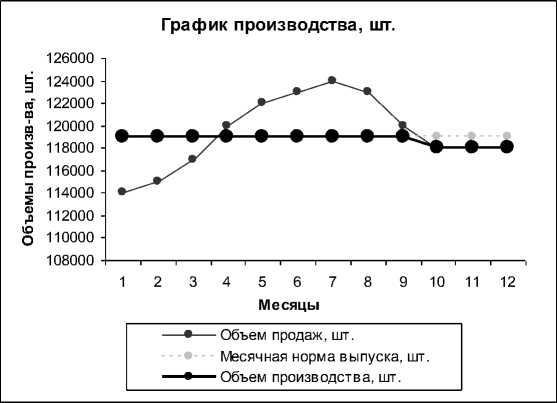
Таблица 6

Программа производства по значениям модели (26) в случае повышения производственной

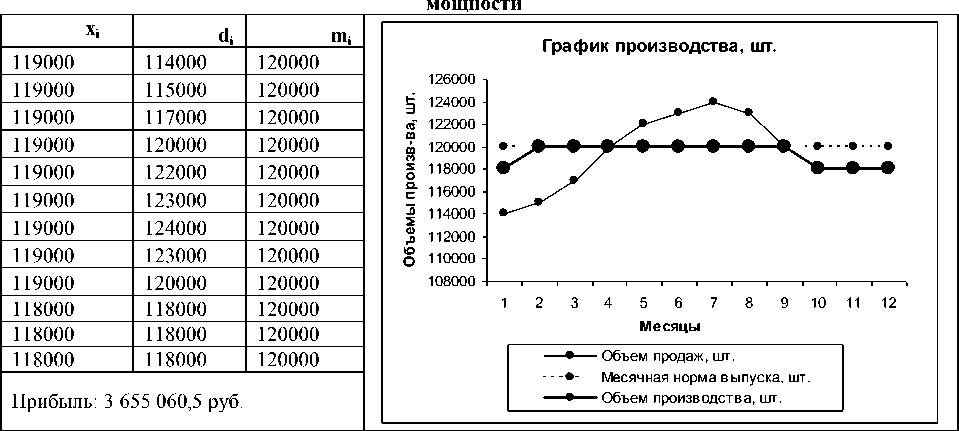
Анализ и сравнение результатов в табл. 2 и 5, 4 и 6 позволяет сделать вывод о том, что при стратегии закупки фиксированного объема за счет уменьшения величины партии расходы на содержание запасов сырья уменьшились, а прибыль увеличилась. Выводы о загрузке производственных мощностей и об остатках готовой продукции, сделанные для стратегии периодических закупок, имеют место и при использовании стратегии закупки фиксированного объема.

Сравнение моделей (25) и (26) позволяет сделать вывод, что существенное влияние на прибыль оказывает размер партии закупаемого сырья. Если затраты на выполнение заказа не слишком велики, то можно закупать сырье мелкими партиями. В случае больших затрат на выполнение заказа слишком частые закупки приведут к повышению общих затрат, тогда выгоднее осуществлять закупку большими партиями, причем на такие объемы возможна скидка со стороны поставщика.

Аналогичные выводы были сделаны

Уилсоном при выводе формулы оптимального размера заказа. Рассчитаем для нашего примера размер оптимальной партии для заказа:

2 ⋅ 5 ⋅ 2.5 ⋅ 1432000

0.03 ⋅ 12

≈ 9972 кг.

Отметим, что полученный объем получился сравнительно небольшим и поставщику обычно невыгодно поставлять в таких объемах. Результаты расчета программы производства с использованием оптимального размера заказа представлены в таблице 7.

Таблица 7

Программа производства по значениям модели (26) в случае использования формулы

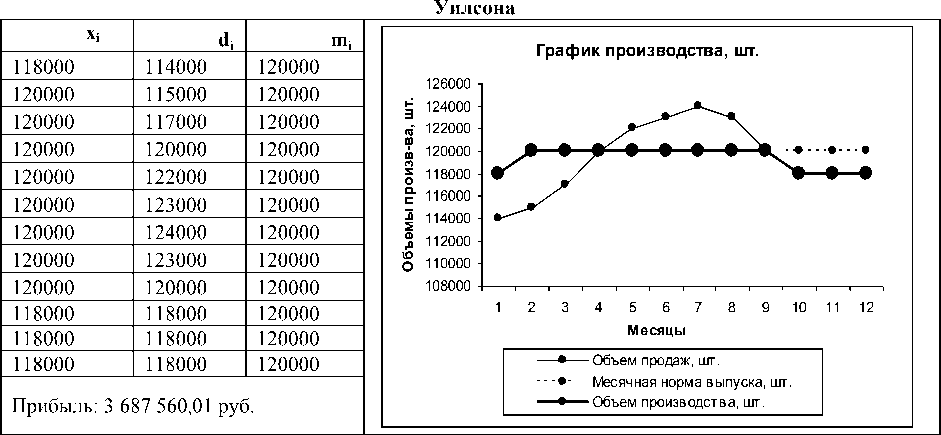
Анализ результатов в табл. 4, 6, 7 позволяет сделать вывод, что при использовании формулы Уилсона прибыль увеличилась. Так, если при взаимодействии предприятия с поставщиком не накладываются ограничения на поставки продукции, то эффективнее использовать формулу Уилсона, иначе вполне оправданно использовать стратегию закупки фиксированного объема с заданным объемом q . При высокой стоимости поставки необходимо сравнить прибыль, получаемую при использовании обеих стратегий, и принять решение [1]. Вполне возможно, что более выгодной будет стратегия периодических закупок.

Анализ построенных моделей формирования производственной программы керамического кирпича свидетельствует, что производственные мощности и объемы ожидаемых продаж оказывают существенное влияние на объемы и ритмичность выпуска продукции, а построенные модели обеспечивают нахождение оптимального плана при фиксированных значениях параметров. При изменении производственных мощностей в сторону увеличения растет их недозагрузка, что отражается на упущенной прибыли. Потому при выборе оптимального сценария производства керамического кирпича, если возможно регулирование производственной мощности предприятием, необходимо правильно соотнести уровень загрузки производственных мощностей, получаемую прибыль, остатки готовой продукции на конец периода планирования и принять решение.

Выводы

Построены детерминированные динамические модели производства в условиях детерминированного описания среды. Модели позволяют получить оптимальные график производства, объемы закупок сырья, выявить резервы производственных мощностей, определить, обеспечено ли производство необходимым сырьем (материалами), оценить затраты, прибыль. Основным достоинством моделей является подбор наилучших параметров производства продукции и объемов закупки сырья при заданных ограничениях.

Приведены примеры моделей производства керамического кирпича, проанализированы полученные результаты. Показано, что построенная модель по сравнению с производством по среднему значению объемов продаж обеспечивает получение большей прибыли, требуется меньше запасов на складе к концу периода планирования.

Построенные модели могут служить базой для разработки других моделей, с учетом новых ограничений и специфики производства, в частности для разработки стохастических, многопродуктовых, нечетких моделей.

Построение подобных моделей имеет, на наш взгляд, огромное значение для предприятий по производству продукции, так как позволяет объединить процессы производства, поставок, управления запасами и т.д. с целью найти и построить оптимальное решение.