Разработка и проверка двумерной конечно-элементной модели височно-нижнечелюстного сустава при помощи магнитно-резонансного исследования: моделирование движения открытия и закрытия челюстей
Автор: Аун M., Meнар M., Морлье Ж., Рамос A., Монеде-хокуард Л., Сид M.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (51) т.15, 2011 года.
Бесплатный доступ
Двумерная конечно-элементная модель височно-нижнечелюстного сустава создана на основе сагиттальных срезов магнитно-резонасной томографии (МРТ) правого сустава добровольца, который не имел патологий суставов. Движения открывания нижней челюсти моделировались с помощью перемещений относительно черепа. Эти перемещения, реализованные добровольцем, были заранее измерены при помощи трехмерной системы анализа движений. Срезы МРТ при различных расстояниях между резцами челюстей также вначале выполнялись для верификации результатов. Целью данной статьи является описание различных этапов метода: разработка геометрической модели, выбор свойств материалов и граничных условий, проверка конечно-элементной модели. Срезы МРТ при различных расстояниях между резцами челюстей дают возможность подтвердить положение диска при различных этапах моделирования. Первые результаты показывают, что конечно-элементная модель позволяет оценить распределение напряжений в суставе. Наибольшие напряжения по Мизесу были обнаружены в средней части диска.
Диск височно-нижнечелюстного сустава, конечно-элементная модель, моделирование
Короткий адрес: https://sciup.org/146216012
IDR: 146216012 | УДК: 531/534:
Текст научной статьи Разработка и проверка двумерной конечно-элементной модели височно-нижнечелюстного сустава при помощи магнитно-резонансного исследования: моделирование движения открытия и закрытия челюстей
Височно-нижнечелюстной сустав (ВНЧС) – один из самых сложных суставов в человеческом теле. Эта сложность является следствием многих показателей: количество мышц и связок, мобильность суставного диска, нижняя челюсть связана с черепом двумя суставами и т.п. В то же время ВНЧС – все еще один из наименее изученных суставов. Знание функциональной анатомии и биомеханики ВНЧС остается недостаточным, в частности для протезирования.
Аун Mхамад, лектор и исследователь лаборатории механики и физики, Бордо
Meнар Mишель, профессор, заведующий лабораторией механики и физики, Бордо
Морлье Жульен, ассистент профессора лаборатории изучения адаптации движений, Бордо
Рамос Антонио, ассистент профессора кафедры механической инженерии, Авейру
Монеде-Хокуард Люция, студент лаборатории механики и физики, Бордо
Сид Mариано, профессор лаборатории механики и физики, Бордо
В последних исследованиях о ВНЧС предложен метод описания кинематики и суставных действий [9]. Статистические исследования также были реализованы, и были выделены три группы с различными видами кинематики [5].
Некоторые авторы особо интересуются суставным диском и характеристикой структуры и механических свойств [1, 6] для того, чтобы понять их функции. Detamore et al. [6] показали, что диск вовлечен в некоторые дисфункции ВНЧС и что 70% пациентов с дисфункцией сустава имеют вывих диска.
В последнее время конечно-элементный метод стал широко применяться для изучения сустава. Он является хорошим средством для моделирования биомеханического поведения суставов и позволяет определять распределения напряжений и деформаций в различных элементах ВНЧС. Эти данные не доступны in vivo из-за трудностей, связанных с введением экспериментального устройства в естественный сустав. В течение последних десяти лет разработано много конечноэлементных моделей. Авторы смоделировали перемещения нижней челюсти, такие как открывание [7, 8, 13], закрывание [4] и боковое перемещение [12]. Другие авторы создавали конечно-элементные модели, чтобы сравнить распределения напряжений в нормальных и патологических случаях [14]. Конечно-элементный метод также использовался для моделирования механического теста для того, чтобы предложить механический закон поведения суставного диска [2].
Devocht et al. использовали двумерную конечно-элементную модель, чтобы изучить управление смещениями диска при открывании челюстей [7]. Они модифицировали свойства элементов, присоединенных к диску, чтобы оценить их влияние при смещениях диска. То, что открывание челюстей, наложенное на модель, не соответствует геометрии, может изменить результаты и привести к неверным выводам.
Данная статья описывает разработку двумерной конечно-элементной модели ВНЧС и моделирование открывания челюстей. Сначала смоделированные результаты сравнивались со статическими изображениями МРТ, реализованными при различных расстояниях между передними резцами для того, чтобы подтвердить положение и геометрию диска, а затем и конечно-элементную модель. Двумерные модели позволяют проще оценить влияние некоторых параметров, таких как присоединения к диску в определенном положении.
Материал и метод
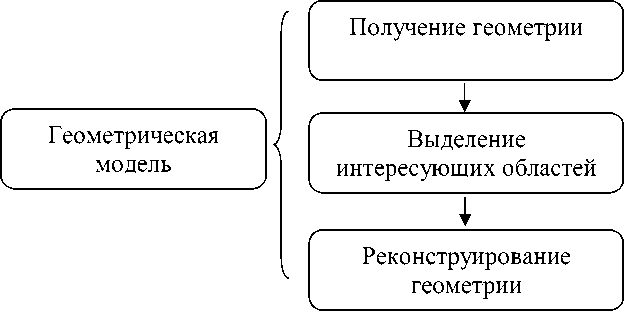
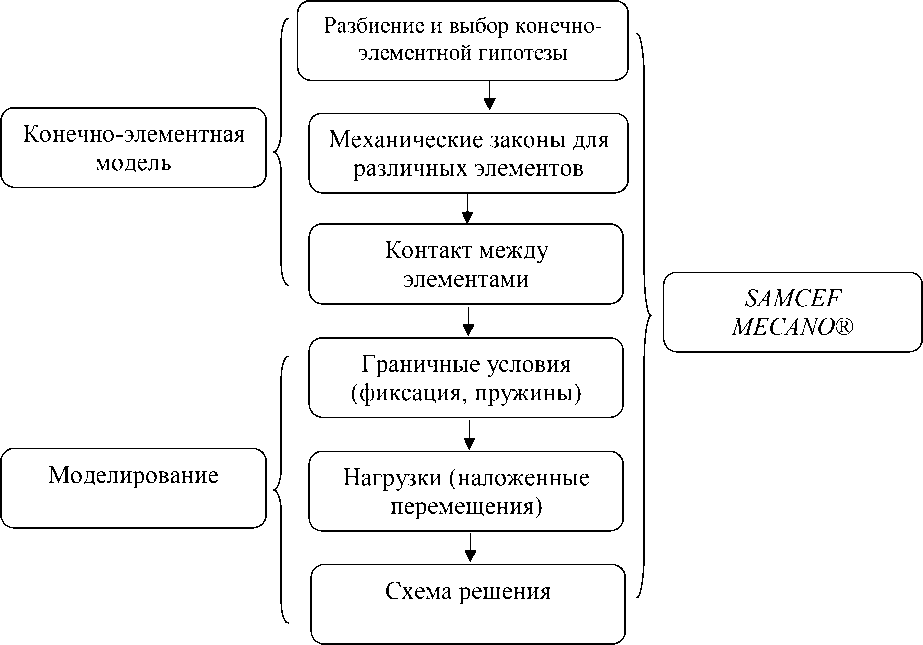
Действия для разработки конечно-элементной модели ВНЧС, а затем и для моделирования открывания челюстей приведены на рис. 1.
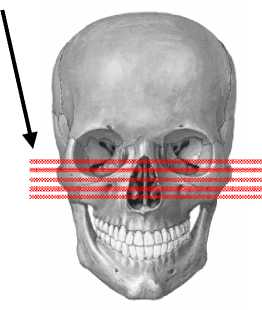
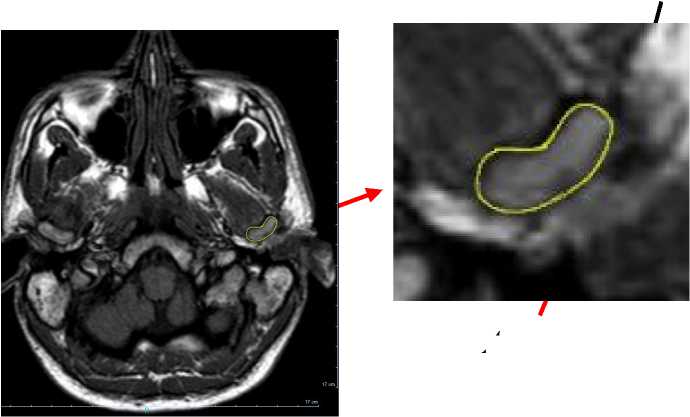
Во-первых, геометрия ВНЧС была получена при помощи МРТ устройства Philips 1,5 Тл. Исследование было выполнено при помощи специализированного манипулятора в больнице Бордо. Полученная плоскость ( A -плоскость) была взята перпендикулярно к медиолатеральной оси ( ML -ось) суставного мыщелка. Эта ось прежде была определена на срезе горизонтальной плоскости (рис. 2).
Геометрия затем была восстановлена при помощи CAD программного обеспечения ( CATIA V 5). Контуры суставного диска, мыщелка и части височной кости были сегментированы в МРТ-срезах до помещения как изображение в программу (рис. 3). Масштаб срезов учитывался в течение фазы импортирования. Схема, представляющая геометрию модели, затем была восстановлена из изображения. Эта схема представляет собой двумерную геометрическую модель ВНЧС, которая состоит из трех элементов: суставного диска, мыщелка и части височной кости. Геометрическая модель затем была экспортирована из SAMCEF® software , где были реализованы сетка и вычисления.
Этап
Техника, программное
|
обеспечение |
|
|
/ |
X МРТ |
|
X____ |
У |
Компьютерная обработка изображений
|
/ |
CATIA V 5 |
X |
|
X____ |
Проверка
Сравнение результатов модели с экспериментом
Рис. 1. Этапы разработки конечно-элементной модели и моделирования процесса открывания челюстей
Сетка модели сформирована только четырехугольными элементами (рис. 4). Эта сетка создавалась автоматически с использованием алгоритма, предложенного в программном пакете. Этот алгоритм применяется к геометрической области с четырьмя гранями, в которой противоположные стороны содержат одинаковое количество узлов. Когда геометрия области становилась слишком сложной, область делилась на подобласти, которые имели простую геометрию. Сетка формируется из X узлов и Y элементов.
ML -ось
Горизонтальные МРТ-срезы
A -плоскость
а
б
в
Рис. 2. Выделение полученной плоскости из МРТ-среза: а – горизонтальные МРТ-срезы; б – горизонтальный срез с выделенной областью сустава; в – увеличенная область сустава
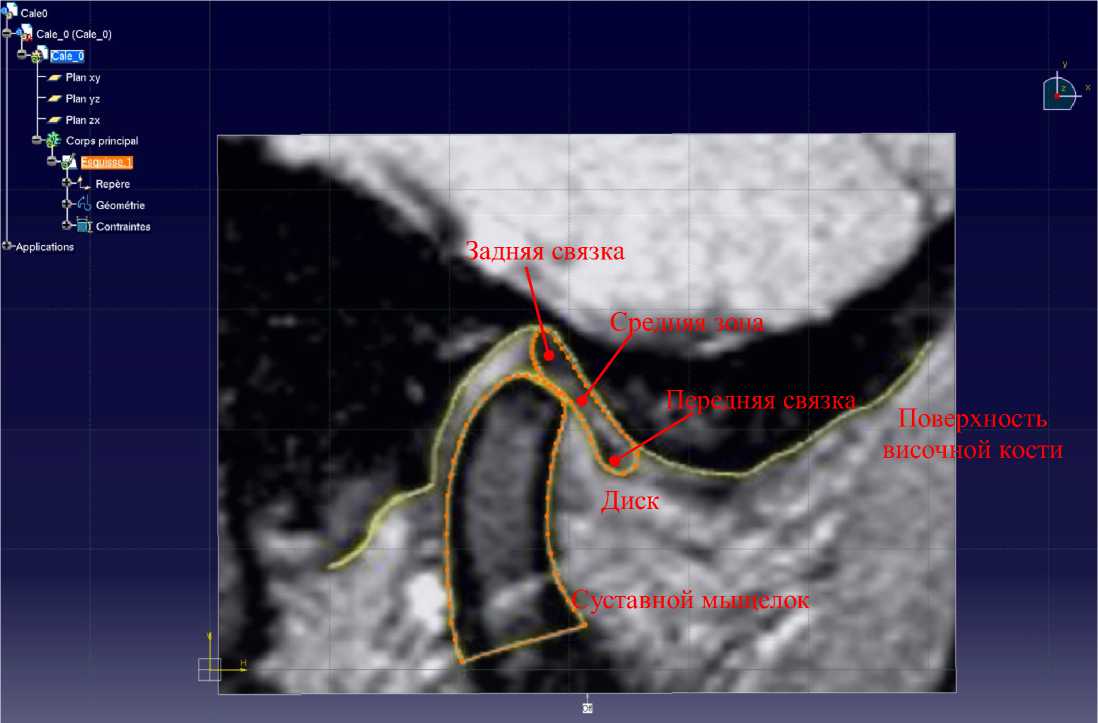
Рис. 3. МРТ-срез, импортированный в CATIA , и реконструирование геометрии
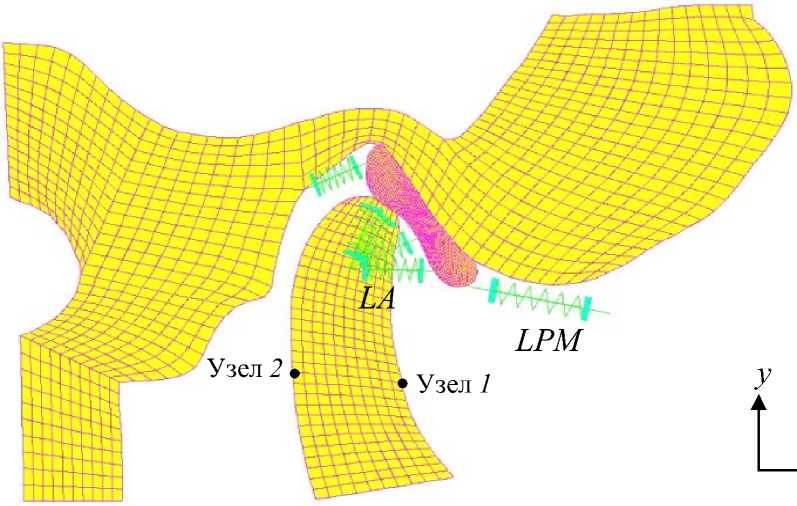
Рис. 4. Двумерная конечно-элементная модель
Сгущение сетки также протестировано для того, чтобы удостовериться, что размер сетки не влияет на результаты. Гипотеза плоскодеформированного состояния была принята, поскольку ML -ось мыщелка больше, чем переднезадняя ось ( AP -ось).
После создания сетки были назначены механические свойства для различных частей модели через механические законы поведения. Кости считались как однородные линейно упругие. Модуль упругости и коэффициент Пуассона были взяты из литературы со значением 14000 MПa и 0,3 соответственно. Считается, что диск является однородным нелинейно упругим и ведет себя как гиперупругое тело согласно закону Муни-Ривлина.
Этот закон определен функцией w плотности энергии деформации и первым, и вторым инвариантами I 1 и I 2 тензора деформаций
w(11,12) = C1(11 -3) + C2(12 -3), где C1 = 27,91 MПa и C2 = –20,81 MПa – константы материалов, определенные из экспериментов [4].
Модель была создана из трех частей: суставного мыщелка, височной кости и суставного диска, расположенного между двумя костными суставными поверхностями. Контактные элементы были расположены между поверхностью мыщелка и нижней поверхностью диска, а также между поверхностью височной кости и верхней поверхностью диска. Эти элементы передавали только нормальные силы. Трение не было принято во внимание из-за существования синовиальной жидкости, смазывающей сустав. Модель взаимодействия была адаптирована к большим перемещениям диска, который свободно мог скользить между суставными поверхностями.
Для того чтобы смоделировать открывание челюстей, соответствующие смещения были наложены на нижнюю челюсть, поскольку мышечная активность, которая реализует данное перемещение, полностью не известна. Эти смещения были предварительно измерены для того же добровольца с использованием устройства анализа движений ( BTS-ELITE ). Смещения на сагиттальной плоскости (рис. 5) были наложены на один узел модели в течение двадцати шагов; статическое вычисление было реализовано для каждого шага. Чтобы смоделировать правильно смещение суставного мыщелка, мы должны задать смещение вдоль оси y (рис. 6) в другом узле для того, чтобы задать вращение мыщелка. Это смещение было вычислено из смещения первого узла и вращения, измеряемых устройством. Для того чтобы не появлялись высокие нежелательные напряжения в зоне, где задавались смещения, смещение вдоль оси x не накладывалось на этот второй узел. В течение моделирования периферические узлы височной кости были зафиксированы.
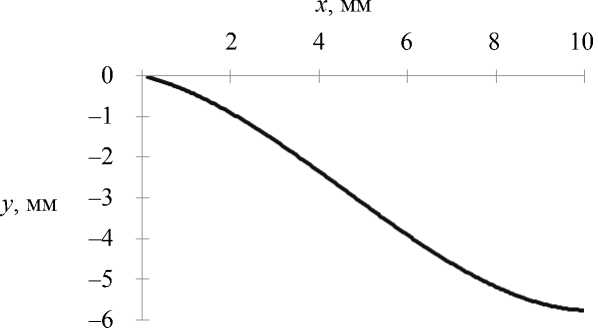
Рис. 5. Cагиттальное перемещение, наложенное на узел 1 модели
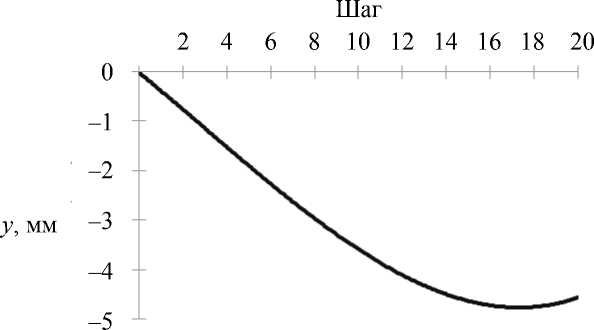
Рис. 6. Перемещение вдоль оси y , наложенное на узел 2 в модели
а б в
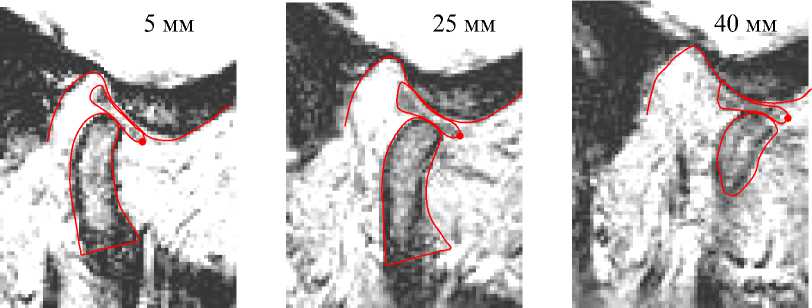
Рис. 7. МРТ-срезы ВНЧС, соответствующие различным расстояниям между резцами: а – 5 мм; б – 25 мм; в – 40 мм
Смещение диска управлялось его присоединениями в окружающей кости и включением мышц на его суставной границе. Существует несколько теорий функциональной анатомии для объяснения управления перемещением диска. Devocht et al. [7] использовали двумерную конечно-элементную модель, чтобы протестировать другие применяемые методы моделирования присоединения диска для понимания механизма смещения диска. Они установили, что диск перемещается даже тогда, когда никакого присоединения не моделируется; учитывается только давление, оказываемое суставным мыщелком. Геометрическая модель и смещения, наложенные на модель, не принадлежат тому же добровольцу. Они накладывали смещение в узле и небольшое усилие в другом узле, чтобы сохранить контакт. Эти приближения могут испортить результаты и привести к ложным выводам. В модели, представленной в этой статье, два типа присоединения диска и одно включение мышц были смоделированы. Первое присоединение имело отношение к задней связке (RDL), которая связывает заднюю границу с височной костью и ограничивает смещение диска вперед из-за заднего усилия. Этот случай был смоделирован линейной пружиной жесткостью 0,2 Н·мм–1 [4]. Латеральные связки (LA) связывают периферию диска с латеральным полюсом суставного мыщелка. Они ограничивают скольжение диска по поверхности суставного мыщелка. Они были смоделированы с использованием четырех линейных пружин, первоначально растянутых с жесткостью, равной 0,2 Н·мм–1. Как было сказано, передняя граница диска получала мускульное включение от латеральной крыловидной мышцы (LPM). Функциональная анатомия представляет противоречивые теории относительно роли этой мышцы при смещении. Недавний электромиографический анализ, проведенный с участием 154 добровольцев, обнаружил, что мышца LPM активна в процессе открывания челюстей [11]. Исходя из этого действие данной мышцы было учтено в модели. Оно было смоделировано линейной пружиной с переменной жесткостью. Пружина давала увеличение усилия на диск, чтобы смещать его вперед.
Сагиттальные МРТ-срезы ВНЧС были выполнены на различных расстояниях между передними резцами. Срезы выполнялись при расстояниях от 5 до 40 мм между резцами. На рис. 7 приведены три образца 5, 25 и 40 мм. Они позволяют сравнить положение диска в процессе моделирования. Положение точки, расположенной на передней границе диска, вычисленное при моделировании, сравнивалось с положением той же самой точки, измеренным на срезах МРТ. Было проведено множество моделирований, в которых жесткость пружины, моделирующей крыловидную мышцу, менялась, пока необходимое положение диска не было получено.
Результаты
Моделирование показывает, что прикладываемые смещения двух узлов являются подходящими для моделирования реальных смещений мыщелка. Диск перемещался и деформировался в соответствии с суставным мыщелком благодаря давлению, приложенному последним, и усилием, оказываемым передней пружиной, моделирующей LPM . Это смещение ограничивалось сзади задней пружиной, моделирующей RDL .
Положения точки, расположенной на передней стороне диска, при различных расстояниях между передними резцами (от 5 до 40 мм с шагом 5 мм), полученные при моделировании и на срезах МРТ, сравнивались (рис. 8). Кривые траекторий, пройденные диском в течение моделирования и полученные с помощью МРТ, хорошо коррелируют. Тем не менее положения показывают, что степень смещения диска в моделировании более высокая в начале, чем измеренная с помощью МРТ. Это означает, что усилие, возникающее в результате действия передней пружины, слишком большое в начале моделирования. Данное положение подтвердает теорию функциональной анатомии, предложенную Caix [3], согласно которой LPM активна только в конце процесса открывания челюстей, чтобы удерживать диск между суставными поверхностями. В дальнейших исследованиях необходимо определить активность этой мышцы для того, чтобы лучше моделировать ее функцию.
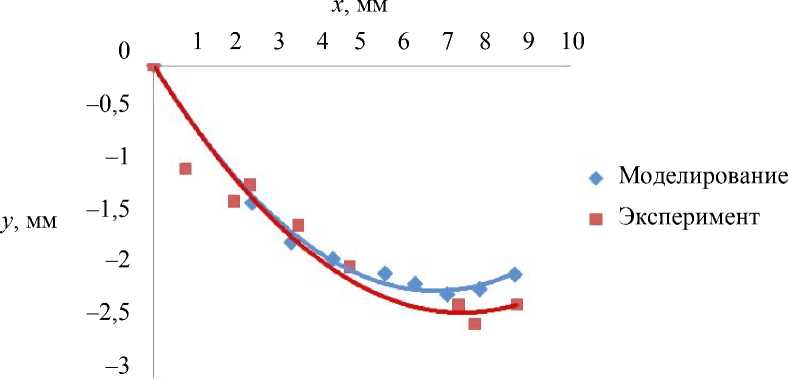
Рис. 8. Положение диска при увеличении расстояния между резцами каждый раз на 5 мм при моделировании и в эксперименте
МПа 9,683 8,715 7,747 6,788 5,81 4,842 3,873 2,905 1,987 0,968 0
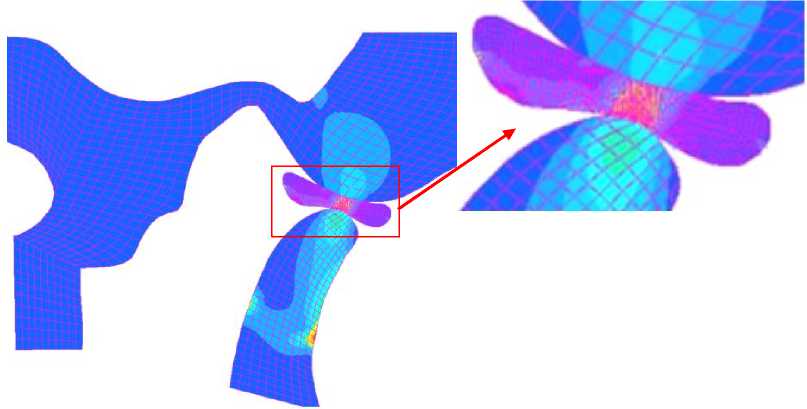
Рис. 9. Напряжения по Мизесу при заключительном шаге (максимально открыты челюсти), полученные при моделировании
5 10 15 20 25 30 35 40
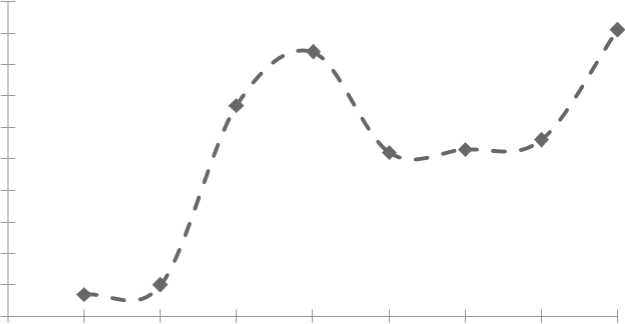
σ VM , MПa
Расстояние между резцами, мм
Рис. 10. Зависимость максимальных значений напряжений по Мизесу от величины расстояния между резцами
Рис. 9 иллюстрирует распределение напряжений по Мизесу в суставе. Более высокие напряжения сосредоточены в промежуточной зоне диска. Рис. 10 показывает изменение максимальной величины напряжений по Мизесу в диске по мере увеличения расстояния. Максимальные величины были получены для расстояния между резцами, равного 20 мм (суставной мыщелок просто смещается вперед относительно височной кости), и при максимальном расстоянии между резцами (суставной мыщелок осуществляет почти чистое вращение). Напряжения в диске были выше, чем в костях, и выше в нижней части диска, чем в верхней. Эти результаты показывают важную роль диска в поглощении и распределении напряжений в суставе.
Выводы
Эта статья показывает различные этапы обработки двумерной конечноэлементной модели и моделирования процесса открывания челюстей. Модель принадлежит к бессимптомному предмету, так что результаты не могут быть обобщены. Некоторые этапы должны быть более детально разработаны для того, чтобы получить определенные количественные величины напряжений. МРТ-срезы были в недостаточной степени связаны. Сложным этапом является момент разграничения и дифференцирования разных областей. Система координат, использованная для трехмерного видеоанализа, должна соответствовать тем же самым срезам МРТ для того, чтобы увеличить точность.
Механический тест in vitro должен быть проведен, чтобы определить реальное механическое поведение диска и RDL . С той же целью деятельность LPM должна быть оценена с использованием EMG [10].
Кроме того, моделирование позволяет охарактеризовать распределение напряжений в суставе в процессе открывания челюстей. Срезы МРТ, исселедованные при разных расстояниях между резцами, допускают проверку положения диска при различных шагах моделирования.
Список литературы Разработка и проверка двумерной конечно-элементной модели височно-нижнечелюстного сустава при помощи магнитно-резонансного исследования: моделирование движения открытия и закрытия челюстей
- Allen K.D., Athanasiou K.A. Viscoelastic characterization of the porcine temporomandibular joint disc under unconfined compression//Journal of Biomechanics. -2006. -Vol. 39. -P. 312-322.
- Beek M., Koolstra J.H., Van Eijden T.M.G.J. Human temporomandibular joint disc cartilage as a poroelastic material//Clinical Biomechanics. -2003. -Vol. 18. -P. 69-76.
- Caix Ph. L'Articulation Temporo-Mandibulaire et son vrai-faux ménisque//Thèse de Doctorat, Université de Picardie, 1991.
- Chen J., Akyuz U., Xu L., Pidaparti R.M.V. Stress analysis of the human temporomandibular joint//Medical Engineering & Physics. -1998. -Vol. 20. -P. 565-572.
- Coutant J.Ch., Mesnard M., Morlier J., Ballu A., Cid M. Discrimination of objective kinematic characters in temporomandibular joint displacements//Archives of Oral Biology. -2008. -Vol. 53. -P. 453-461.
- Detamore M.S., Athanasiou K.A. Structure and function of the temporomandibular joint disc: implications for tissue engineering//Journal of Oral Maxillofac Surg. -2003. -Vol. 61. -P. 494-506.
- Devocht J.M., Goel V.K., Zeitler D.L., Lew D. A study of the control of disc movement within the temporomandibular joint using the finite element technique//Journal of Oral and Maxillofac. Surg. -1996. -Vol. 54. -P. 1431-1437.
- Donzelli P.S., Gallo L.M., Spilker R.L., Palla S. Biphasic finite element simulation of the TMJ disc from in vivo kinematic and geometric measurements//Journal of Biomechanics. -2004. -Vol. 37. -P. 1787-1791.
- Mesnard M., Aoun M., Morlier J., Cid M., Ballu A. Validation of a protocol to characterize the temporomandibular joint kinematics//International Journal for Computational Vision and Biomechanics. -2010. -Vol. 3., No.°1. -P. 25-32.
- Mesnard M., Ballu A., Ramos A., Simoes J.A., Lokhov V.A., Nyashin Y.I. Muscular and articular forces exerted on the human mandible//1st International Conference on Biodental Engineering. Porto. June 2009.
- Murray G.M., Bhutada M., Peck C.C., Phanachet I., Sae-Lee D., Whittle T. The human lateral pterygoid muscle//Archives of Oral Biology. -2007. -Vol. 52. -P. 377-380.
- Pérez del Palomar A., Doblaré M. Finite element analysis of the temporomandibular joint during lateral excursions of the mandible//Journal of Biomechanics. -2006. -Vol. 39. -P. 2153-2163.
- Tanaka E., Rodrigo D.P., Tanaka M., Kawaguchi A., Shibazaki T., Tanne K. Stress analysis in the TMJ during jaw opening by use of a three dimensional finite element model based on magnetic resonance images//International Journal of Oral & Maxillofac Surgery. -2001. -Vol. 30. -P. 421-430.
- Tanaka E., Del Pozo R., Tanaka M., Asai D., Hirose M., Iwabe T., Tanne K. Three-dimensional finite element analysis of human temporomandibular joint with and without disc displacement during jaw opening//Medical Engineering & Physics. -2004. -Vol. 26. -P. 503-511.


