Разработка интеллектуальной системы управления многозвенным роботом манипулятором

Кузнецов Е. А., Ульянов С. В. Разработка интеллектуальной системы управления многозвенным роботом манипулятором // Системный анализ в науке и образовании: сетевое научное издание. 2022. №3. С.161-179. URL:

В современном высокотехнологичном обществе при выполнении проекта типа «Индустрия 4.0» не обойтись без столь же высокотехнологичной техники, процесс создания которой часто требует высокой точности, порой не достижимой для людей. В таких случаях на помощь приходят роботы-манипуляторы.

Робот-манипулятор – созданный для выполнения двигательных и управляющих функций в каком-либо процессе – манипуляционный робот, т. е. полностью автоматическое устройство, состоящее из манипулятора и программируемого контроллера управления, которое вычисляет и генерирует управляющие воздействия, задающие необходимые движения всех двигающих компонентов устройств. Основные области применения - перемещение предметов производства и исполнение разнообразных технологических операций, таких как высокоточная сварка, покраска, резка и прочие достаточно сложные работы, требующие высокой точности.

В большинстве задач манипуляторы выполняют определённые действия, находясь в неизменной среде с чётко просчитанными внешними условиями, и на первый взгляд, в таких случаях использование интеллектуальной системы нецелесообразно, достаточно набора определённых положений, которые позволяют выполнить поставленную задачу. Однако, при этом не учитываются отличные от начальных условия – старение механизмов, изменение масс и длин звеньев и мн. др. Более того, существует множество задач, требующих более сложного и робастного управления, отражаемого в программном обеспечении системы управления – в том числе, позволяющее работать в отличных от расчётных ситуаций.

В качестве вычислительного фундамента, для такого ПО, используются технологии мягких вычислений – нечёткие контроллеры с переменными параметрами управления, нейронные сети и генетические алгоритмы. Применение мягких вычислений позволяет наделить систему управления такими качества как адаптация и обучение, что, по своей сути, отражает свойства интеллектуальной системы управления (ИСУ).

В данной работе представлены вариант применения технологии мягких вычислений в задаче управления многозвенным манипулятором без обратной связи, где обучение проводит сам оператор.

Традиционная система управления робота манипулятора

Традиционная система управления представляет собой совокупность одного или нескольких объектов управления (ОУ) и управляющей системы. В общем случае система управления состоит из звена регулирования, ОУ, а также интеллектуальной системы (ИС). Для обеспечения заданных динамических показателей в системах управления находят применение различные типы регуляторов. Широкое распространение получили П-пропорциональные, ПИ-пропорциональные интегральные, ПД-пропорциональные    дифференциальные,    и    ПИД-пропорциональные    интегрально дифференциальные регуляторы. Интегральная составляющая регулятора позволяет устранить в системе статическую ошибку, а дифференциальная составляющая – улучшить динамические показатели, форсируя переходный процесс.

Для пояснения работы ПИД-регулятора в применении к роботу манипулятору с тремя степенями свободы рассмотрим систему управления с обратной связью и ПИД регуляторами для каждого звена манипулятора. На рис. 1 введены следующие обозначения: εi - ошибка регулирования (отклонение величины от заданной) – подаётся на вход ПИД-регулятора, Kпi, Кдi, Киi– коэффициенты усиления пропорциональной, дифференциальной и интегральной составляющей ПИД-регулятора соответ- ственно, i – номер соответствующего звена робота манипулятора, ui– управляющее воздействие – выходной сигнал ПИД-регулятора, qi– регулируемая величина – угол поворота звена манипулятора.

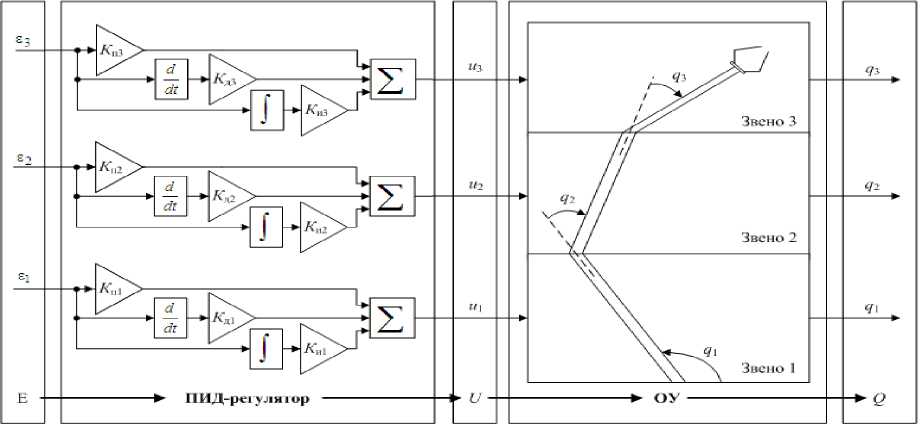
Рис. 1. Система управления с обратной связью на основе ПИД-регулятора.

Рассмотрим особенности ИСУ роботом-манипулятором.

Интеллектуальная система управления робота манипулятора

Основным отличием интеллектуального робота-манипулятора от традиционного является возможность выполнить поставленную задачу в нештатных и изменяющихся условиях, при отличных от начальных параметров, таких как вес, скорость ветра, освещённость. Эти параметры предъявляют некоторые требования к системам управления. Наиболее важные из них можно выделить:

• -    Наличие автоматической подстройки к изменяющимся параметрам системы и объекта управления.

• -    Сохранение работоспособности в условиях неопределённости.

• -    Прогнозирование развития возможных событий.

• -    Возможность организации процесса самообучения на основе обобщения и анализа результатов в процессе функционирования;

• -    Наличие человеко-машинного интерфейса.

Главная особенность интеллектуальной системы управления (см. рис. 2), которая отличается от системы, построенной по «традиционной» схеме, - подключение механизмов хранения и обработки знаний для выполнения требуемых от системы функций в частично определённых или неопределённых условиях при случайном характере внешних возмущений.

Применение технологий мягких вычислений в интеллектуальном управлении позволяет:

• -    Генетическим алгоритмам проводить глобальную оптимизацию структуры и параметров нейронных сетей; проводить формирование обучающих выборок, для дальнейшего использования при генерации базы знаний (БЗ).

• -    Нечётким контроллерам – изменить параметры управления на основе интегрируемой (встраиваемой) базы знаний.

• -    Нейронным сетям – проводить процесс обучения ИСУ.

При этом важно отметить, что источниками данных могут быть:

• -    математические модели, в том числе 3D модели, рассчитанные на суперкомпьютере;

• -    физические модели и макеты, учитывающие особенности реализации (шумы и задержки в каналах связи, люфты и зазоры и многое другое.

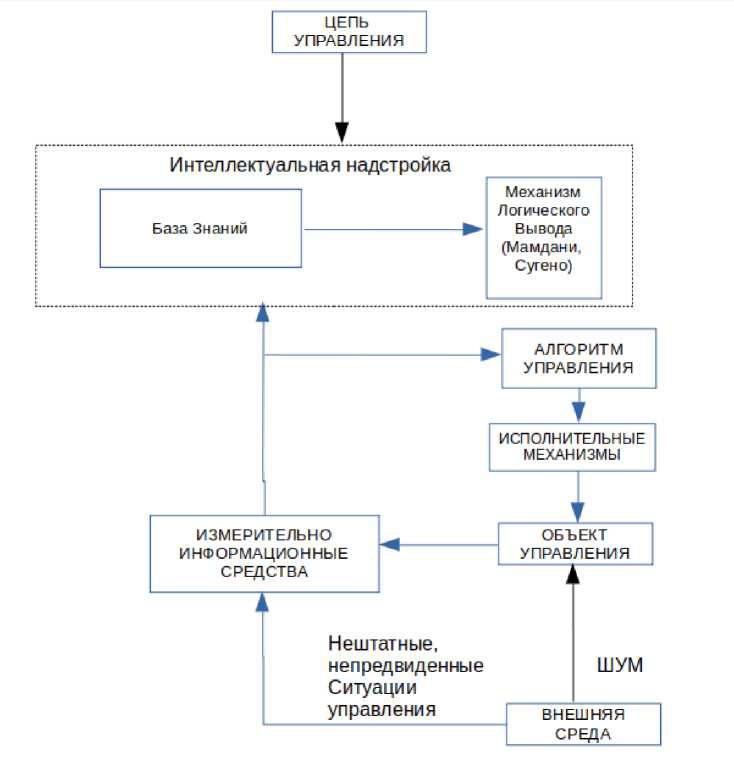
Рис. 2. Обобщённая концептуальная структура интеллектуальной системы управления

Математическая модель позволяет просчитать множество различных ситуаций, но даже самая точная из них имеет некоторые отличия от реального объекта управления. С другой стороны, физическая модель требует эксперта, который участвует в процессе получения данных и подтверждает корректность результата и контролирует процесс обучения на всех этапах работы манипулятора.

Проектирование ИСУ с применением Оптимизатора Баз Знаний на основе технологии мягких вычислений

Основным элементом ИСУ с применением технологий мягких вычислений является нечёткий регулятор (НР), управляющий коэффициентами усиления ПИД-регулятора. НР осуществляет управление за счёт интегрированной в него БЗ, включающей данные о виде и параметрах функций принадлежности входных и выходных нечётких переменных, а также набор нечётких продукционных правил.

Создание БЗ производится с помощью интеллектуального инструментария Оптимизатор Баз Знаний на основе мягких вычислений в следующей последовательности:

• -    создание обучающего сигнала – определение типовой ситуации управления (например, штатная ситуация) формирование таблицы коэффициентов ПИД-регулятора и ошибок управления с помощью ГА;

• -    формирование модели нечёткого вывода – определение типа нечёткой модели, интерпретации нечётких операций, числа входных и выходных переменных;

• -    создание лингвистических переменных для входных значений;

• -    создание базы нечётких продукционных правил;

• -    настройка базы нечётких продукционных правил;

• -    оптимизация левых и правых частей правил БЗ.

На рис. 3 и 4 приведены два возможных варианта реализации ИСАУ на ОБЗ на мягких вычислениях для управления роботом манипулятором с тремя степенями свободы:

• -    ИСАУ на ОБЗ на мягких вычислениях с одним НР и соответственно одной БЗ (рис. 3)

• -    ИСУ на ОБЗ на мягких вычислениях с разделенным управлением (тремя независимыми НР – одна БЗ управляет одним звеном), рис. 4.

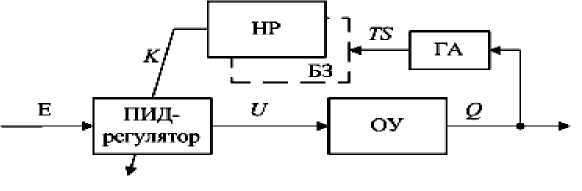
Рис. 3. ИСУ на ОБЗ на мягких вычислениях с одним НР

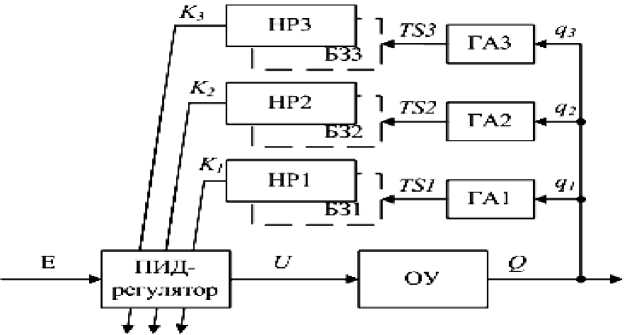
Рис. 4. ИСУ на ОБЗ на мягких вычислениях с разделенным управлением (с тремя НР)

В данной работе реализован вариант с одним НР и одной БЗ.

Рассмотрим более подробно процесс создания БЗ для ИСАУ на ОБЗ на мягких вычислениях с одним НР.

Создание обучающего сигнала - ОС.

Первоначально необходимо определить типовую ситуацию управления. В качестве типовых ситуаций управления можно рассматривать штатные ситуации управления.

В рабочем пространстве робота манипулятора выделим группу из десяти точек, которые определим, как штатные ситуации управления (рис. 5).

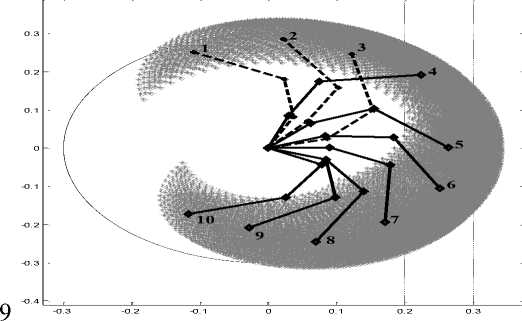
Рис. 5. Тестовое пространство

За начальное положение манипулятора принимается конфигурация: q 1 = 90 град; q 2 = 0 град; q 3 = 0 град.

Для создания ОС были использованы три эксперимента (из штатных), для каждого из которых были созданы ОС1, ОС2 и ОС3, для чего с помощью MatLab / Simulink моделей были воспроизведены ситуации управления, в которых параметры ПИД-регулятора определялись с помощью ГА.

На рис. 6 в качестве примера приведён ОС1, на котором: в левом столбце [err P 1 , err D 1 , err I 1 , err P 2 , err D 2 , err I 2 , err P 3 , err D 3 , err I 3 ] – вектор входных переменных пропорциональных, дифференциальных и интегральных ошибок первого, второго и третьего звеньев манипулятора, в правом столбце [ K P 1 , K D 1 , K I 1 , K P 2 , K D 2 , K I 2 , K P 3 , K D 3 , K I 3 ] – вектор выходных переменных (определённых ГА) пропорциональных, дифференциальных и интегральных коэффициентов ПИД-регулятора первого, второго и третьего звеньев манипулятора соответственно.

Итоговый ОС, используемый для получения БЗ состоит из последовательно соединённых ОС1, ОС2 и ОС3.

Формирование модели нечёткого вывода.

В этом случае конкретизируется:

• -    тип нечёткой модели: Сугено 0 (нулевого порядка);

• -    интерпретация нечётких операций – нечёткая конъюнкция как произведение;

• -    число входных и выходных переменных: 9 и 9.

Создание лингвистических переменных для входных значений .

С помощью ГА в составе ОБЗ определяются оптимальное число и форма функций принадлежности.

При создании БЗ первоначально было задано создание пяти функций принадлежности для каждой из девяти входных переменных, т.е. вектор [ n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 n 9 ] = [5 5 5 5 5 5 5 5 5], что привело бы к созданию n 1 × n 2 × n 3 × n 4 × n 5 × n 6 × n 7 × n 8 × n 9 = 1953125 нечётких правил.

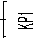
¹5⁰0⁰0⁰ fM^ wlW ^^ ikk i' ^

00     50    100150

iteration

-50 "                     I

-100

0     50    100    150

iteration

0
2000
4000

0 0     50    100    150200

iteration

0     50    100    150    200

iteration

	0 -20 -40 100	"mjvv^vw'1jT^vT
		50    100 iteration	150	200
	0 -100	/Г~Ни'^
	0     50    100 iteration		150	200

1500000 ММЙУУМ^

0 0     50    100    150200

iteration

0 0     50    100    150200

iteration

5000 0	.~ ^ vwVT / ^ i-n-r/ ь^-
-5000
0	50    100	150    200
	iteration

¹5⁰0⁰0⁰ уук ?“Mw^X Ш¹¹J

0 0     50    100    150    200

iteration

	20 0 -20	У~»хлллЬ^	„ллЛ1\АгЛг1	1	1 ^
		0     50	100	150	200
			iteration
	100		----
	0	L^vA f\l\jur	„ n I v.rAj-.^ ..^
	-100	0     50	100	150	200
			iteration
	5000
	0		1-1 ' v /-i Гх ! '-.r\
-	5000	0     50	100	150	200
			iteration
	20 0 -20	p^wwwv V^-!"-wv7 '^ ^ i Л Г LT
		0     50	100	150	200
			iteration

500 0

0 0     50    100    150    200

iteration

500000 PPWnFWyy {

0 0     50    100    150    200

iteration

0     50    100    150    200

iteration

Рис. 6. ОС1 для ИСУ на ОБЗ с одним НР

После работы ГА вектор [ n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 n 9 ] принял значение [4 4 4 4 3 4 4 3 3], а максимальное число нечётких правил составило 110592 (на рис. 7 приведены число и форма функций принадлежности для входных переменных 1 – 3) .

Рис. 7. Функции принадлежности для входных значений 1 – 3 (K P1 , K D1 , K I1 )

Создание базы правил .

Благодаря использованию алгоритма отбора правил (прохождение заданного порога активации), из 110592 правил были отобраны 33 наиболее робастных.

Настройка базы правил. Оптимизация левых и правых частей правил БЗ.

Используется традиционный метод обратного распространения ошибки.

Вид созданной БЗ для Выхода 1 приведён на рис. 8.

Рис. 8. БЗ: пример для Выхода 1

В данном разделе приводилась зависимость максимального числа нечётких правил от количества функций принадлежности для входных переменных n i : максимальное число нечётких правил для созданной ранее БЗ при трёх-четырёх функциях принадлежности составляло 110592 правил. Предположим, меньшее количество функций принадлежности – для каждой входной переменной равное трём. Тогда зависимость максимального числа нечётких правил от числа степеней свободы манипулятора имеет вид, приведённый на рис. 9.

Рис. 9. Зависимость максимального числа нечётких правил от числа степеней свободы манипулятора

При необходимости введения дополнительных звеньев, расширения функций уже существующих или добавления прочих устройств, требующих координационного управления, каждая степень свободы будет увеличивать максимальное число нечётких правил более чем на полтора порядка. Это приводит к увеличению сложности создания БЗ, и, как следствие, увеличению времени создания БЗ, повышению требований к вычислительным ресурсам процессора, на котором создаются БЗ и объёму памяти системы, в которой размещается БЗ.

При возникновении ситуаций, когда сложность реализации единой БЗ высока, одним из реальных выходов может быть разделение БЗ на несколько, соответственно использовать не один НР, а несколько НР. Например, возможно использование предложенной ранее ИСАУ на ОБЗ на мягких вычислениях с тремя независимыми НР (рис. 4).

Управление манипулятором без обратной связи на основе мягких вычислений

Рассмотрим пример использования мягких вычислений для управления манипулятором без обратной связи

Рис. 10. Общий вид робота манипулятора

Выбран манипулятор с 6 степенями свободы общей длиной 51 см. Управление сервоприводами манипулятора осуществляется через плату расширения, установленную в основании. Манипулятор подключён по USB -кабелю к компьютеру (ПК). Над манипулятором стационарно закреплена камера, передающая изображение в ПО системы распознавания. Общий вид системы камера - стационарный манипулятор приведён на рис. 11.

Рис. 11. Общий вид системы манипулятор - камера. 1 — USB-камера, 2 — манипулятор, 3 плата расширения для питания сервоприводов, 4 - плата Arduino Nano для связи с ПК

Программирование микропроцессора, управляющего сервоприводами манипулятора

Всё аппаратное обеспечение робота размещается на двух печатных платах – плата электропитания сервоприводов и плата управления, выполняющая формирование сигналов ШИМ (широтноимпульсная модуляция и связь с ПК ( Arduino Nano ). Плата управления подключена к плате электропитания как модуль расширения через разъем.

Плата Arduino Nano имеет связь с ПК через USB-serial порт, следовательно, имеется возможность управлять роботом дистанционно (через дистанционное подключение к управляющему ПК). Сервоприводы двигаются с максимальной для себя скоростью из-за чего движения робота становятся резкими, отрывистыми. Чтобы сделать движения робота более плавными в ПО управления приводами была добавлена задержка в 10 мс при каждом повороте привода на 1градус. Также на низком уровне была запрограммирована возможность изменения последовательности запуска приводов при сложном движении, т. е. когда задействованы все 6 из имеющихся.

Так, при одном типе движений приводы включаются в последовательности 6, 5, 4, 1, 3. А при другом в последовательности, например, 1, 4, 3, 6, 5. Тип движения задаётся через протокол общения робот – ПК.

Захват объекта манипулятором

Задача захвата объекта манипулятором решается с помощью системы распознавания ( computer vision – CV ). Система распознавания состоит из USB -камеры и ПО обработки изображения от USB -камеры. В качестве объекта захвата был выбран цветной кубик из набора детских игрушек, как лёгкий предмет, хорошо выделенный цветом на рабочей поверхности. Система распознавания выделяет объект по цвету, передаёт координаты объекта – кубика в программу управления манипулятором. Далее ПО манипулятора, обращается в базу знаний, полученную от Оптимизатора Баз Знаний через мягкие вычисления, и получает значения углов сервоприводов, которые соответствуют положению манипулятора в точке захвата кубика. Далее робот перемещает захват - механизм в заданную точку с помощью своих приводов.

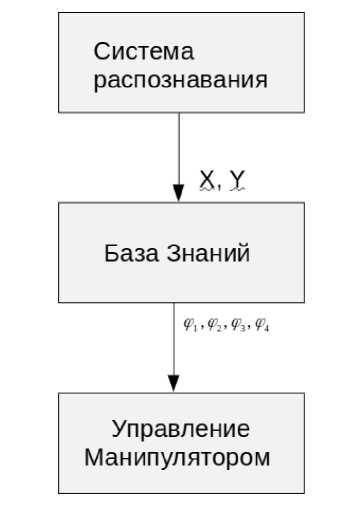
Рис. 12. Алгоритм захвата объекта манипулятором.

Стек ПО распознавания объекта и ПО управления манипулятором.

Система распознавания определяет координаты центра (X, Y) объекта и передаёт их в ПО манипулятора, где определяются значения углов сервоприводов.

Было принято решение не объединять эти задачи в один программный продукт, а иметь два отдельных и создать между ними стек. При этом каждый из программных модулей может использоваться с любой другой задачей, что делает эти модули более универсальными.

Организация межпрограммного взаимодействия, реализуется через механизм клиент-сервер, использующий unix socket.

В unix-подобных системах механизм сокетов применяется для обмена данными между процессами операционной системы.

Есть 2 типа сокетов:

• -    AF_UNIX ( unix domain ) для обмена внутри файловой системы через файловый дескриптор

• -    AF_INET ( internet domain ) для обмена по телекоммуникационной сети, через протокол tcp/ip .

В данном случае был использован тип сокета AF_UNIX , т.к. оба процесса работают на одном и том же ПК, соответственно, используют общую файловую систему.

Именно через механизм сокетов ПО распознавания (сервер) получает запрос от робота (клиент), обрабатывает его и выдаёт обратно в сокет ответ – координаты X , Y центра объекта. Отметим, что другой тип сокета – AF_INET был использован в дальнейшем при организации взаимодействия роботов по сети через технологию клиент-сервер, см. раздел «Дистанционное управление роботом».

Как уже было отмечено выше, система распознавания вынесена в отдельную программу. Она работает в четыре потока: один поток отвечает за считывание кадров с камеры, второй за вывод картинки в пользовательском интерфейсе, третий – сокет-сервер и четвёртый HTTP -сервер. В начале программы происходит загрузка в память основных параметров: диапазоны значения цветовых каналов и номер камеры, затем осуществляется подключение к камере. Далее в бесконечном цикле происходит получение кадров с камеры и последующий анализ алгоритмом детектора. Результаты детекции подвергаются фильтрации – не все размеры объекта являются допустимыми и результат детекции должен быть стабильным на протяжении заданного количества кадров. В результате работы детектора на кадре, полученном с камеры, рисуется прямоугольник, который обводит найденную область объекта. Если область успешно прошла фильтры, то прямоугольник будет зелёный, в противном случае – красный. После фильтрации результаты детекции записываются в состояние сокет-сервера, кадр с визуализацией работы алгоритма записывается в состояние HTTP -сервера. Сокет-сервер хранит информацию о статусе детекции (найден/отсутствует), положении объекта ( Х и У координаты в пикселях) и его размерах (длина и ширина в пикселях). Алгоритм работы программы представлен на рис. 13.

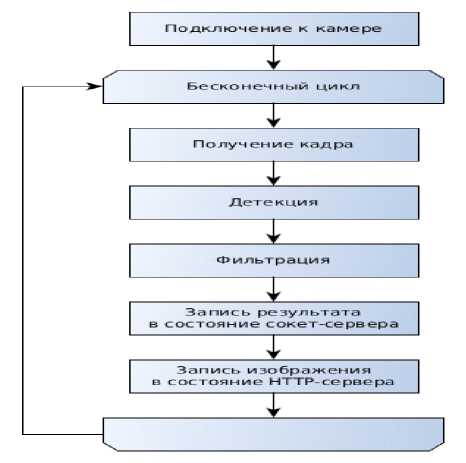
Рис. 13. Алгоритм ПО распознавания.

Пользовательский интерфейс реагирует на управление с помощью манипулятора типа мышь и клавиатуры. Горячие клавиши:

• -    s – сохраняет текущий кадр в файл;

• -    с – включение режима калибровки цветовых диапазонов объекта (объект можно выделить с помощью манипулятора типа мышь);

• -    Esc или q – выход из режима калибровки / закрытие программы

Описание алгоритма детекции системы распознавания

Алгоритм принимает на вход изображение. Каждый пиксель проверяется, удовлетворяют ли значения его цветовых каналов заданным диапазонам. Если не удовлетворяют – пикселю присваивается чёрный цвет. Далее применяется алгоритм выделения контуров, входящий в библиотеку с открытым исходным кодом OpenCV (Satoshi Suzuki and others. Topological structural analysis of digitized binary images by border following. Computer Vision, Graphics, and Image Processing, 30(1):32–46, 1985). Из полученных контуров выбирается максимальный по площади. Площадь контуров рассчитывается по формуле Грина 's_theorem#Area_calculation). Далее для максимального по площади контура определяется описывающий его прямоугольник (координаты верхнего левого угла, длина и ширина). Данный прямоугольник и является результатом работы алгоритма детекции. В случае, если не было найдено контуров с площадью больше 100 кв. пикселей, процедура возвращает прямоугольник с нулевым размером. Алгоритм работы детектора системы распознавания представлен на рис. 14.

Пользовательский интерфейс программы может быть переведён в режим калибровки цветового диапазона искомого объекта. Для этого можно нажать кнопку « c » английской раскладки клавиатуры. В верхнем левом углу кадра появится надпись « COLOR CALIBRATON ». В этом режиме пользователь может выделить искомый объект с помощью левой кнопки мышки. Как только кнопка мышки будет отпущена будет запущен анализ цветов выделенного диапазона пикселей, а пользователь увидит анимацию и надпись « CALIBRATION DONE !». Выйти из режима калибровки можно выполнив выделение области объекта, либо с помощью кнопок Esc или q . Пример того, как выглядит калибровка представлен на рис. 15.

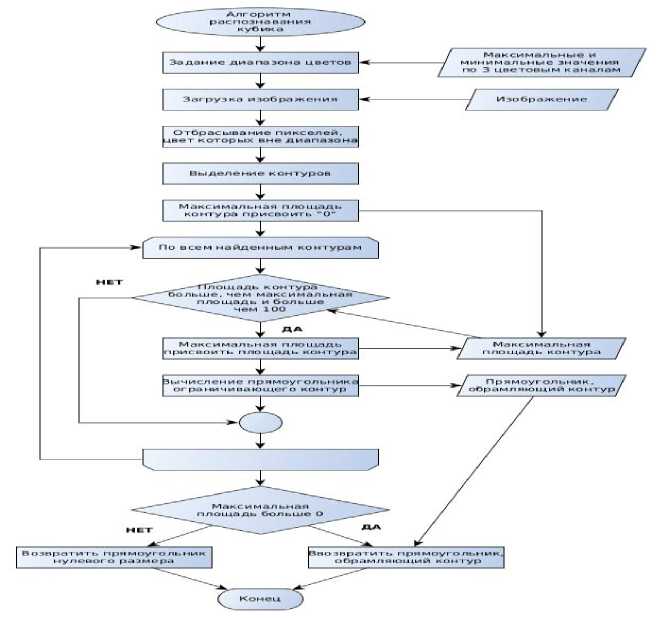
Рис. 14. Алгоритм работы детектора системы распознавания

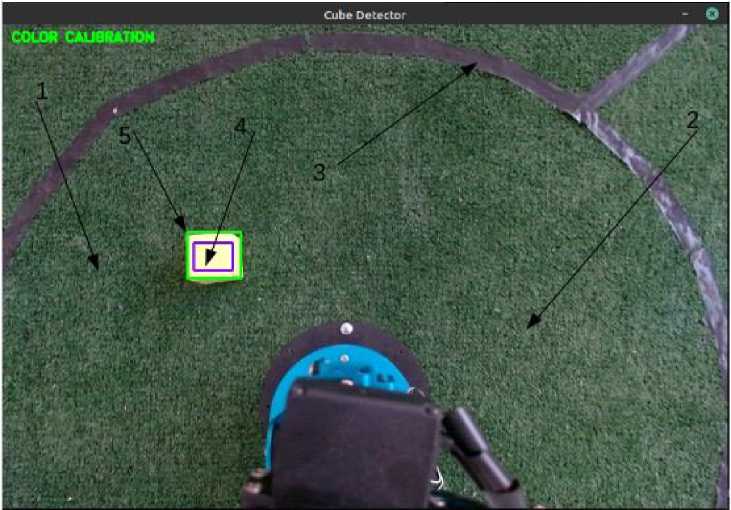
Рис. 15. Окно программы в режиме калибровки: 1,2 – Рабочая область манипулятора, 3 – Граница рабочей области манипулятора. 4 – Ручная калибровка по цвету объекта с помощью «мышки» (фиолетовый прямоугольник), 5 – Выполнена детекция объекта, поэтому он выделен зелёным прямоугольником

Под анализом цветов выделенного диапазона пикселей понимается выделение минимального и максимального значения каждого цветового канала пикселей внутри выделенного диапазона. По каждому каналу выбираются минимальные и максимальные значения, затем минимальное значение уменьшается на константу, а максимальное значение увеличивается на эту константу. При этом проводится проверка, что полученные значения не выходят за границы допустимых значений цветового канала пикселя - интервал [0, 255].

Результатом работы алгоритма являются координаты центра объекта для распознавания, которые поступают в нечёткую нейронную сеть, где в дальнейшим рассчитываются значения углов манипулятора.

ПО создания обучающей выборки

ПО создания обучающей выборки разработано для формирования связанных множеств значений {координаты кубика} и {набор значений углов серводвигателей}, где координатам центра кубика сопоставляются углы сервоприводов робота. Эти значения являются обучающим сигналом для ИСУ манипулятора. Обычно, подобное ПО включает в себя:

• -    GUI ( Graphical User Interface ) пользователя с возможностью разметки исходных данных.

• -    Протокол обмена и взаимодействия непосредственно с объектом интеллектуализации.

• -    База данных для хранения и дальнейшего использования размеченных данных.

Разработка интерфейса пользователя

Для облегчения процесса создания обучающей выборки был разработан соответствующий пользовательский интерфейс на языке C ++ с использованием библиотек Qt , обладающий следующим функционалом:

• -    Регулировка значений угла для каждого привода через кнопки ( spinbox в терминах Qt ), либо обычный ручной ввод;

• -    Сохранение текущих значений координат центра кубика и соответствующих им углов в строку (файл) для передачи в Оптимизатор баз знаний (ОБЗ), собственно, и есть содержимое обучающей выборки.

• -    Обратная операция - передача значений углов из строки ввода (из файла) в соответствующие сервоприводы для последующей быстрой проверки точности (базы знаний) БЗ.

• -    Постановка робота в различные фиксированные позиции (начальное положение, "парковка" перед выключением, точка «выгрузки» кубика)

• -    Считывание ответа от робота через последовательный порт для обработки и принятия решений.

• -    Запись в лог всех команд роботу и ответов робота.

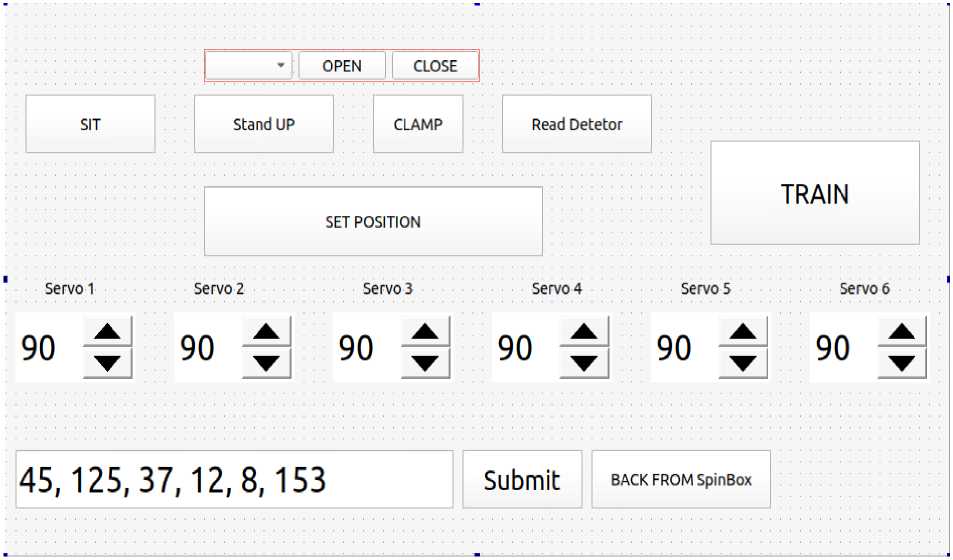
Рис. 16. Пользовательский интерфейс ПО создания обучающей выборки

Создание обучающей выборки

Для формирования обучающего сигнала определяется рабочая область манипулятора — пространство, в границах которого манипулятор гарантировано может взять кубик. Выбраны точки в рабочем пространстве манипулятора, зафиксированы значения углов сервоприводов, соответствующие положению манипулятора для взятия объекта распознавания. Таким образом мы получили обучающий сигнал для использования в Оптимизаторе Баз Знаний (ОБЗ): 2 входа (координаты x, y центра объекта распознавания) и 4 выхода (4 значения угла сервопривода). В дальнейшим, в режиме эксплуатации, координаты x, y поступают от системы распознавания.

Одна из точек обучающей выборки показана на рис. 17.

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т .е. непосредственно из результатов измерений динамических параметров физической модели ОУ, что и было выполнено в данной работе.

Рис.17. Робот в одной из точек обучающей выборки

ОС является источником знаний и представляет собой массив данных, разделённый на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В случае аппроксимации некоторого управляющего сигнала, входными компонентами могут являться координаты объекта манипулирования ( х , у ), а выходными компонентами – требуемое значение угла каждого звена (рис. 18).

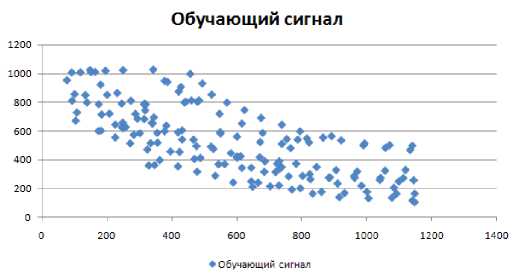
Рис. 18. Обучающий сигнал

Результатом аппроксимации ОС является построенная БЗ для НР, включающая оптимальное конечное множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР.

Согласно теореме об аппроксимирующих свойствах ННС, полученный нечёткий регулятор имеет БЗ со свойством универсального аппроксиматора не доопределённых свойств исследуемого плохо формализованного объекта со скрытыми параметрами. На основе полученных обучающих данных, был спроектирован встраиваемый контроллер для управления звеньями манипулятора (см. Приложение).

На рисунке 19 представлена структура нечёткой нейронной сети (ННС), реализующая модель нечёткого логического вывода Сугено, представлены также нечёткие множества описывающие входные данные – координаты объекта для манипулирования. На рисунке 19 справа, представлена поверхность управляющего воздействия, вырабатываемого нечётким логическим выводом, и иллюстрирующая выходные значения для углов манипулятора.

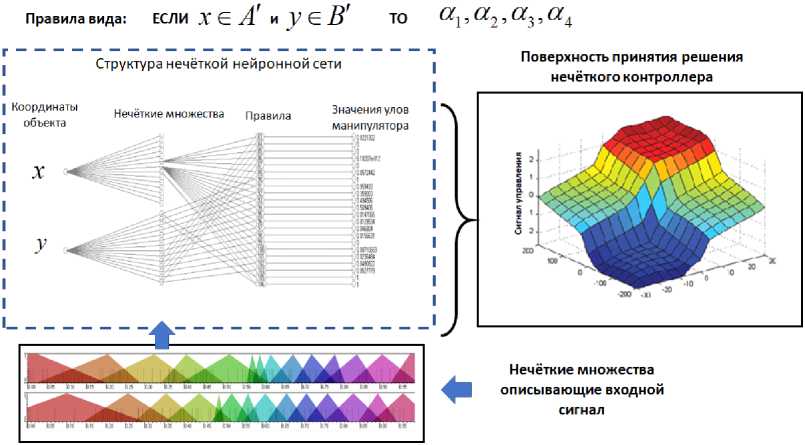
Рис. 19. Структура базы знаний в виде нечёткой нейронной сети .

Оптимизатор Баз Знаний – программный инструментарий, основанный на технологиях мягких вычислений и стохастического моделирования, предназначен для извлечения, формирования и оптимизации баз знаний, был рассмотрен выше.

Структурно Оптимизатор баз знаний (ОБЗ) на мягких вычислениях состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ и содержит следующие шаги алгоритма оптимизации:

Шаг 1: Выбор модели нечёткого вывода . На первом этапе необходимо установить входные и выходные переменные в нечёткую нейронную сеть (ННС) . В нашем случае, для управление манипулятором, имеем 2 входные переменные – координаты центра объекта. Выходными переменными являются значения углов звеньев манипулятора — 4 переменных. В качестве модели нечёткого вывода возможно применять модели нечёткого вывода Сугено, Мамдани, и т.д.). В данном случае используется модель Сугено.

Шаг 2: Создание лингвистических переменных . С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления её функций принадлежности (треугольная, Гауссовская и т.д.). При этом, на основе обучающего сигнала формируется оптимальная структура первого слоя нейронной сети. Применительно к данной задаче это лингвистические переменные для координат X, Y, описывающие положения кубика в кадре. Из рисунка (предыдущего) видно, что используются по 14 треугольных функции принадлежности для каждой координаты. Количество терм - множеств и их тип выбираются автоматически.

Шаг 3: Создание базы правил . На данном этапе возможно создание полной базы правил (как в данном примере) или возможно использовать специальный алгоритм отбора наиболее «робастных правил» в соответствии с заданными критериями качества.

Шаг 4: Оптимизация базы правил. С помощью ГА2 оптимизируются правые части правил БЗ. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага 5 это решение может быть локально улучшено. Правые части правил описывают конкретное значения угла для каждого звена манипулятора.

Шаг 5: Настройка базы правил . С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных (с точки зрения заданной функции пригодности ГА).