Разработка критерия качества прогнозирования биржевых котировок для поддержки принятия решений металлотрейдера

DOI:

Металлургический комплекс России играет важную роль в мировой торговле металлами. На долю данного сектора в российской экономике приходится около 17 % общего объема отгруженной продукции собственного производства. Помимо металлопродукции отгружаются также ломы цветных металлов. Соответственно, экспортная торговля, как ломами металлов, так и готовой металлопродукцией, является крупным сектором экономики в стране [8].

Учитывая важность данного сектора для экономики России, можно сделать вывод о том, что и задачи, стоящие перед металлоторговыми компаниями, также актуальны. Одной из них является прогнозирование цен на металлы, которое осуществляется для различных целей. Практической целью металлоторговых компаний является прогнозирование направления изменения цен, то есть определение знака тренда.

Основные гипотезы и обозначения

В качестве подтверждения данного суждения приведем пример. Один из способов реа- лизации продукции заключается в том, что металлоторговые компании заключают стандартный договор на поставку металла через i дней (на практике обычно i = 14) по цене, которая сложится на LME на момент отгрузки. Предполагается, что объем товара, согласно каждому договору, одинаковый. Также предположим, что компания имеет возможность заключать по одному такому договору каждый день. Пусть исполнение договора предполагает, что в момент его подписания закупается необходимый объем товара, который далее реализуется через i дней второй стороне договора. Если лицо, принимающее решение, использует максимальную возможность по частоте подписания договоров (то есть заключает их каждый день), то величина прибыли металлоторговой компании за какой-либо период будет зависеть в первую очередь от характера изменения цен на данную продукцию. Повлиять на величину дохода в положительную сторону можно при заключении договоров в благоприятные моменты времени, то есть в те, когда с момента подписания до момента реализации цена выросла. Поэтому знание ожидаемого тренда поможет избежать заключения невыгодных контрактов.

Таким образом, зная, какая будет цена, компании смогут выбирать один из двух вариантов: заключить или отклонить тот или иной контракт. Инструментами для поддержки принятия решения выступают модели прогнозирования. Чем они точнее, тем правильнее будет принятое решение. Для определения наиболее качественных моделей прогнозирования и их применимости на практике необходим критерий отбора.

Таким образом, при заключении контракта необходимо знать будущее направление тренда. Естественно предположить, что на любом отрезке времени компания будет иметь прибыль, если количество прибыльных сделок превышает количество убыточных, в противном случае компания понесет убытки. Если же количество убыточных сделок равно количеству прибыльных, то на данном отрезке прибыль компании будет нулевой. Как показано выше, прибыльная сделка возможна в случае правильного прогнозирования знака изменения цены. Соответственно, модель должна быть такой, чтобы знак изменения цены больше чем в 50 % случаях был верно определен .

Для понимания процесса принятия решений с помощью прогнозирования рассмотрим рисунок 1. Первый прогноз осуществляется в момент времени t = 1 – i на момент времени t = 1, где i – период упреждения. При этом для построения модели прогнозирования необходима обучающая выборка – это область L с длиной l на рисунке 1. Далее эта область сдвигается на 1 момент времени вперед, следовательно с учетом замены самого старого значения новым пересчитываются параметры модели и осуществляется второй прогноз в момент времени t = 2 – i на момент t = 2. Таким образом, построив N прогнозных значений, последнее из которых будет рассчитано в момент времени t = N – i на момент t = N , можно оценить качество модели прогнозирования на тестовой выборке – на области B с длиной N .

Если точность модели удовлетворит критерию качества, то в момент времени t = N можно принимать решение о заключении контракта на основе данной модели прогнозирования.

На практике существует множество показателей качества модели прогнозирования. Выбор каждого конкретного из них определяется поставленной задачей. В нашем случае наиболее уместен такой показатель, как средняя абсолютная процентная ошибка:

£ l y t - y J

A = -^—^У 100%,        (1)

N где yt – фактическое значение временного ряда в момент t; yˆt – прогнозное значение на момент времени t; N – количество прогнозных значений [6].

На эту величину в различных источниках накладывают разные ограничения, при удовлетворении которым говорят о высоком качестве модели. Одни исследователи считают, что точность прогноза высокая, когда средняя ошибка прогноза меньше 8 %, другие ставят на эту величину ограничение сверху, равное 10 %. Более того, некоторые исследователи считают модель точной, когда данная ошибка не превышает 15 %. Наиболее распространенные в литературе ограничения на среднюю относительную ошибку прогноза приведены в таблице 1.

Таблица 1

Связь точности прогноза и средней абсолютной процентной ошибки

A , %	Точность прогноза
< 10	Высокая точность
10–20	Хорошая точность
20–50	Удовлетворительная точность
> 50	Неудовлетворительная точность
Примечание. Составлено по: [7].

На практике о точности модели можно судить только исходя из конкретных целей.

l		i	N – 1
	L		B
t =	1 – i – l	t = 1 – i            t =	1                           t = N              t

Рис. 1. Отрезок принятия решения

В нашем случае основной целью прогнозирования цен на металлопродукцию является правильное определение направления изменения цены с вероятностью, превышающей 0,5, для того чтобы металлотрейдер был в прибыли. Тогда выясним, какой должна быть средняя абсолютная процентная ошибка у моделей, чтобы обеспечить этот результат.

Рассмотрим такую величину, как среднее абсолютное значение темпа прироста за период упреждения прогноза:

дем сравнивать между собой числители. Тогда:

A _ I — ^— y .| • y . — i

yt • y t—i

_T _ I — ^— — — i l • — yI • yI — i

.

(3.1)

(4.1)

N

z t_. i

yt

—

У. - i

У . — i

N

• 100%,

где y_t , y_{t – i} – фактическое значение временного ряда в момент времени t и t – i соответственно; i – длина периода упреждения, с которой будет делаться прогноз; N – количество прогнозных значений.

Из таблицы 2 видно, что однозначно поставить знак между A и T в формулах (3.1) и (4.1) можно в случаях, представленных на рисунках 2 ( а ) и 5. В остальных ситуациях соотношение между средней абсолютной процентной ошибкой и средним абсолютным значением темпа прироста зависит от соотноше-нийзначений y . — i , y_t , y . .

Рассмотрим для рисунка 2 ( б ), при каких фактических и прогнозном значениях временного ряда A = T. Знак модуля в формулах (3.1) и (4.1) извлекаем, исходя из соотношения

Разработка условий для средней относительной ошибки прогнозирования

yˆ yt—i < y. < y . Тогда A _ T ^ —

^ У .

—

2 y_. = ^y.

—

У . • У . — i

y . — i

—

y, _ У

—

Уt—i     »^

y y2

^ y, ^_ —. y. — i

y . — i

Следова-

На данном этапе можно выдвину т ь г и потезу: если для модели прогнозирования A <  T , то вероятность правильного прогнозирования знака изменения цены этой моделью больше 0,5 ( p >  0,5). При каждом прогнозировании возможны 4 варианта исхода события: 1) при росте цены направление предсказано верно; 2) при росте цены направление предсказано неверно; 3) при падении цены направление предсказано верно; 4) при падении цены направление предсказано неверно.

Для того чтобы сравнить A и T между собой для всех четырех исходов, необходимо вначале рассмотреть формулы (1) и (2) средней абсолютной процентной ошибки и среднего абсолютного значения темпа прироста соответственно. Исключив операцию усреднения этих величин, выпишем их формулы для единичной операции прогнозирования:

тельно, если y . >  ——, то A > T , в

У.—i случае A < T. Для рисунка 3 A _ T ^ —

противном

yt

—

y,— i

_ y . —

. — i

t

—

—

y ² y . ^_ —

^— У t _

y

—

y. • y.—i      - ₌

t

y.—i y. • y.—i      -* = 2• y. • y.—i

t

y.— i

y.— i

—

y ²

^t . Тогда

если y_t <  y * , то A > T , в противном случае A <  T Для рисунка 4 ( а ) граничное значение y ˆ ^* нахо-

А           —, - У, дится следующим образом: A _ T ^ ——— _ y

y.— i

—

yt      yt

— ^-

—

yt

y . — i         y. — i- y t

_ — •(y t—i- yt) ^ — y —i

y

^_---^_ y .

У . — i

У . • У . — i

— y =

—

- y . ^{2 +} y . • y . — i ^ y . — i

A _ I—t——I, y ,

T |y. - y.—il T _ y.—i

^ y * _ ² • ^y. •^y . ^{— i}

—

—. A < T при y_t <  y * , и A > T

.

Далее приведем формулы (3) и (4) к наименьшему общему знаменателю и бу-

y.—i в противном случае. Наконец, для рисунка 4 (б).

A _ T ^ ^—.— y

y .     y . — i

—

У . — i

— ^ y .

—

~ ₌ y. • y. - i ^y .

—

—2. ^

У,— i

^ y _ У . • y . - i ⁺ y .

—

y . — i

У . • y . — i

2 y ²

^ y , _ ' y . — i

.

Здесь

если y_t >  y * , то A < T , и наоборот.

Таблица 2

Связь исходов события прогнозирования с соотношением между A и T

1. При росте цены направление предсказано верно

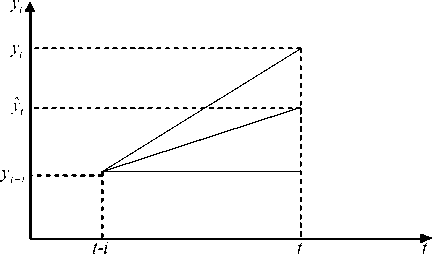
Рис. 2 ( а ). Цена поднялась, направление угадано

^{( y}, <  У , )

У , — i < ^y; , <  У , ^ | ^y , ^— У , I < I У , ^— У , — i| У , — i <  У , ^,

.

Тогда A < T yt

У,—i yt

ˆ yt—i yt y t ^ yt—i y t, при этом

или ^yt

—

ˆ*

yt

—

^{y £ —} i I, или l ^y£

—

)⁾ t - y , | < | y , - y , — i l

^, y , | >| УI ^— УI — i |.

Пусть ^y t y . Тогда если ^y t > ^y t ,

противном случае A < T

ˆ

ˆ*

то A > T , в

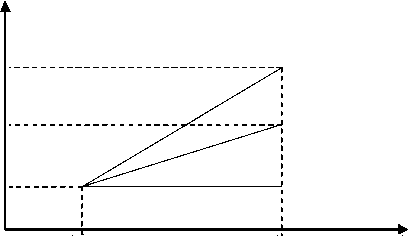
Рис. 2 ( б ). Цена поднялась, направление угадано ^{( y} , >  У I )

yt

yt

У , — i

л yt

• 2.    При росте цены направление предсказано неверно

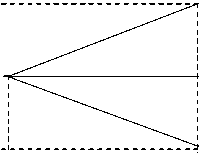
t-i

t

t

yt <  у , — i <  у , .

• - * _ ² • У , • У , — i

Пусть ^y t       y

—

^{y 2}                            *

. Тогда если ^yt <  ^yt , то A >

T , в противном случае A < T

Рис. 3. Цена поднялась, направление не угадано

• 3.    При падении цены направление предсказано верно

  

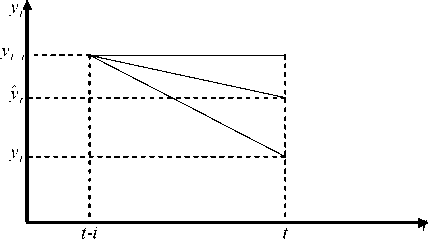
  Рис. 4 ( а ). Цена опустилась, направление угадано ___________________________ ^{( y}. > y , ) ___________________________

  
  

• У , <  ^y_t< y_t — i .

• „ * _ ² • y , • y , — i

Пусть У‘        у _ yt—i

—

_{y t} 2                              _*

. Тогда если y <  ^y , , то A <

T , в противном случае A > T

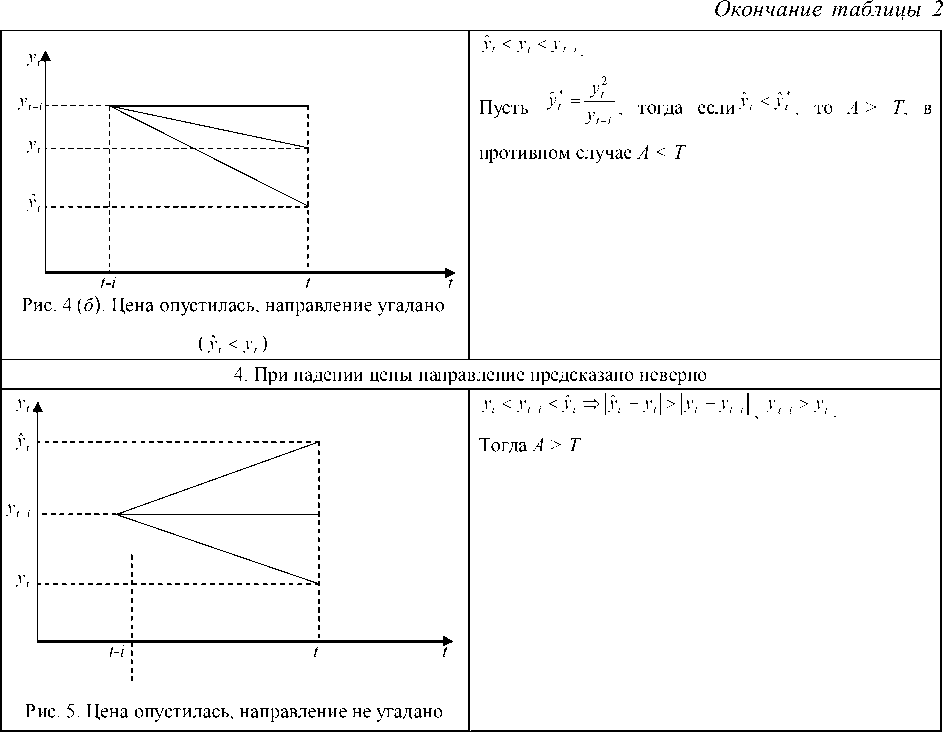
Таким образом показано соотношение A и T между собой в каждом из четырех исходов события прогнозирования. Для наглядности продемонстрируем результаты в таблице 3.

Рассмотрим все случаи, когда A < T. При таком условии знак изменения цены может быть предсказан верно в двух из трех случаев. Тогда вероятность правильно спрогнозировать тренд равна 3. При этом вероятность обратного события (направление движения цены спрогнозировано неверно) соответственно равна 3. При A > T знак изменения цены будет предсказан верно в двух из четырех случаев, то есть вероятность правильно спрогнозировать тренд равна 2, обратная вероятность также будет равна 2. И, наконец, при A ® T вероятность того, что знак изменения цены предсказан верно, равна при обратной 13

вероятности в 3.

Однако, как видно из таблицы 3, ситуация A < T может также возникнуть и в случае, когда направление движения цены предсказано неверно. В частности, если при росте цены спрогнозирован спад. Это утверждение отражается в величине вероятности правильного прогнозирования направления движения цены при A < T . Именно из-за возникновения данной ситуации эта вероятность равна ₃, а не 1.

Другими словами, даже если A < T , с полной уверенностью нельзя сказать, что направление движения цены спрогнозировано верно. Рассмотрим теперь вместо среднего абсолютного значения темпа прироста за период упреждения, представленного в формуле (2), модифицированный средний абсолютный темп прироста за период упреждения:

T ^*

N 2	yt - У t - i
t = 1	yt

N

• 100%.

Сравнив между собой формулы (2) и (5), можно увидеть, в чем заключается отличие. Если в формуле (2) мы рассматриваем абсолютный прирост цены за период упреждения по отношению к значению, которое было в момент прогнозирования ( y_{t – i} ), то в формуле (5) прирост рассматриваем по отношению к значению цены, установленной в момент, на который сделан прогноз ( y_t ).

Аналогично по рисункам 2–5 сравним между собой A и T^* для единичной операции прогнозирования. Результаты сравнения приведены в таблице 4.

Как видно из таблицы 4, ситуация, когда A <  T * возникает в двух вариантах исхода события прогнозирования и в обоих направление изменения цены предсказано верно. Следовательно, если A <  T * , то вероятность того, что знак изменения цены предсказан верно, равна 1. Другими словами, если A <  T\ то с полной уверенностью можно сказать, что направление изменения цены спрогнозировано верно, в отличие от ситуации, когда A < T.

Ситуация, когда A >  T * , может возникнуть для всех 4 вариантов исхода события прогнозирования, при этом направление движения цены предсказано верно лишь в двух из них, следовательно при A >  T * вероятность априори определить верно знак изменения цены составляет 0,5.

Таким образом, как при A <  T , так и при A <  T * вероятность априори верно определить знак изменения цены больше 0,5. Это значит, что при торговле на отрезке времени, на котором A <  T ( A <  T *), количество прибыльных сделок будет больше количества убыточных, что принесет прибыль металлотрейдеру.

На данном этапе сделаем предположение о том, что биржевые котировки цен на металлы являются независимыми случайными величинами. Ведь в противном случае, если бы каждое значение цены зависело от предыдущего, задача прогнозирования не стояла бы так остро. Тогда легко можно было бы рассчитать точное прогнозное значение цены в зависимости от ее предыдущих уровней. Согласно закону больших чисел всегда найдется такое конечное число испытаний, при котором с любой заданной наперед вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности [3]. То есть при A < T(A < T*) с увеличением количества сделок число прибыльных сделок будет больше убыточных, так как вероятность правильного определения знака изменения цены больше 0,5. Это говорит о том, что компания получит прибыль, если для принятия решений будет использовать прогнозную модель, качество которой удовлетворит разработанному критерию.

Заключение

Для подтверждения полученных результатов в работе [4] была апробирована методика прогнозирования цены на никель на товарном рынке с учетом цены фьючерсного контракта на его поставку. В большинстве обучающих выборок выполнялось условие A <  T * . Как следствие, фактическая доля правильно спрогнозированных направлений движения цены превысила 0,5. При этом при прогнозировании в момент 11.10 2016 г. на момент времени 31.10 20 1 6 г. были получены сле д ую щ ие результаты: A = 0,77 %; T * = 1,28 % ( A <  T *), направление изменения цены было спрогнозировано верно.

Таблица 3

Соотношение A и T между собой

Исходы	Соотношение A и T
Цена поднялась, направление предсказано верно	A < T , A > T или A = T
Цена поднялась, направление предсказано неверно	A < T , A > T или A = T
Цена опустилась, направление предсказано верно	A < T , A > T или A = T
Цена опустилась, направление предсказано неверно	A > T

Примечание. Составлено автором.

Соотношение A и T^* между собой

Исходы		Соотношение
Цена поднялась, направление предсказано верно	У, <  У,	A <  T *
	У , >  У ,	A <  T *, A = T *, A >  T *
Цена поднялась, направление предсказано неверно		A >  T *
Цена опустилась, направление предсказано верно	У , >  У ,	A <  T *
	У , <  У ,	A <  T *, A = T *, A >  T *
Цена опустилась, направление предсказано неверно		A >  T *

Примечание. Составлено автором.

Таблица 4

Также следует отметить, что на тестовом периоде направление изменения цены было спрогнозировано верно в 67,44 % случаях. Это говорит о том, что торговля в указанный период принесла бы прибыль металлотрейдеру. Таким образом, модель прогнозирования, удовлетворяющая выдвинутому критерию качества, способна обеспечить коммерческий успех.