Разработка математических моделей испытательных систем как объектов с сосредоточенными параметрами

Химико-технологические системы включают в себя большое число элементов и узлов, в том числе приборы и приборные комплексы, отличающиеся разнообразием функциональных и тепловых связей между ними.

Основным методом проектирования сложных систем является блочно-иерархический, при котором в процессе проектирования система рассматривается последовательно на разных уровнях иерархии с постепенно нарастающей степенью детализации [1].

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

Отличительной особенностью моделирования процессов теплообмена, осуществляемого при проектировании, является необходимость рассмотрения процесса одной и той же физической природы для химико-технологической системы (ХТС) в целом и ее частей. При этом необходимо учитывать тепловые связи между элементами, принадлежащими блокам более высоких уровней иерархии, в которых протекают функциональные процессы различной физической природы [2]. Тепловая модель такой сложной системы, в общем случае, представляет собой комбинацию многочисленных областей сложной конфигурации с источниками и стоками теплоты, в которых движутся потоки теплоносителей (газов или жидкостей).

В общем случае, математическая модель теплового режима объекта записывается в виде системы многомерных нестационарных уравнений теплопроводности для твердых тел ат c p-T=v(x^t)+qv.,z'=i,-,i (1) о t ‘ и уравнений энергии для потоков теплоносителей

С уд. P l \ -T + v v T, J = V ( X . v T, ) ,i = 1, .... L (2) с граничными условиями 1, 2 и 3-го родов либо с условиями сопряжения на границах раздела элементов. В уравнениях (1), (2) использованы следующие обозначения: T , T_l – температуры твердых тел и теплоносителей; t – время; c уд - удельная теплоемкость; p - плотность; X - теплопроводность; q _v - объемная плотность теплового потока; V - скорость движения теплоносителя; I , L – число тел и потоков теплоносителей.

Реализация такой полной модели затруднительна даже с применением современной вычислительной техники, что связано с большим объемом исходной информации для построения полной модели. Анализ теплового режима ХТС часто проводится в условиях, когда внутренняя структура подсистем еще детально не определена.

Моделирование теплового режима ХТС проводится поэтапно с постепенным переходом от верхнего уровня иерархии к нижнему, имеющему в своем составе простейшие подсистемы – отдельные элементы, которые невозможно разделить, не нарушив их целостности. Определяются осредненные характеристики температурных полей тел и потоков теплоносителей, при этом ограничиваются анализом только среднеобъемных и среднеповерхностных температур тел, теплоносителей. Расчет температурных полей тел и потоков теплоносителей проводится на основе моделей с сосредоточенными параметрами [7–10].

В основу модели с сосредоточенными параметрами положено допущение о том, что градиенты температуры по всем направлениям отсутствуют [3, 4]. При этом предполагается, что каждый элемент рассматриваемой системы может иметь тепловые связи как с окружающей средой (конвекцией и теплопередачей), так и с другими элементами системы. Принимается, что в элементе может рассеиваться собственная мощность, а также мощность, подводимая для терморегулирования элемента, которая зависит от его температуры.

В общем случае расчет нестационарного теплового режима по моделям с сосредоточенными параметрами сводится к решению систем уравнений теплового баланса с начальными условиями, т. е. к решению задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка.

Рассмотрим модель системы тел и потоков теплоносителей, находящихся во взаимном теплообмене. В исследуемом объекте выделяют области трех видов:

NT – область твердых тел, температурные поля которых считаются равномерными (Т (t). i = 1..... Nt ); NЖ – объемов с протекающими в них жидкими или газообразными теплоносителями, имеющими среднерасходные температуры на входе Tlвх (t) и на выходе Т[вых (t) и осредненную по объему температуру

Т ( t )( l = 1.

...,

Nж); NСР - область сред с из- вестными температурами Тк'ср (t), k = 1,..., N„.

В твердых телах и в объемах с теплоносителями могут действовать источники теплоты с полными тепловыми потоками q ^T и q_l ^Ж соответственно. Твердые тела находятся в теплообмене друг с другом, а также с теплоносителями и

_ T - T со средами. Тепловые потоки q j , приходящие к данному телу от соседних тел, от теплоносителей qT -Ж и от сред qT - СР, можно выразить через разности их средних температур, в виде:

q T ^{- Т} = K T ^{- Т} ( ^Т, - T i ) F j ^{- Т} .

q iT ^{- ж} = K T ^{- ж} ( T_t - Т ) F T ^{- ж}

,

Т - СР _ Г^Т - СР / С^СР   т \ Г-Т - СР qik = Kik    (Tk     Ti) Fik

,

г t - t где K ij

- Т - Ж Г- - СР il ,Kik   – коэффициенты тепло- передачи между телами i и j, телом i и теплоносителем l, телом i и средой k соответственно,

Т - Т TT - Ж Г- - СР

F_ij , F_il , F_ik – площади контакта между телами i и j , телом i и теплоносителем l , телом i и средой k соответственно.

Корректность зависимостей (3) во многом определяется выбором коэффициентов теплопередачи, зависящих от тепловых проводимостей элементов. Способы вычисления конвективных, лучистых и контактных тепловых проводимостей для разных систем рассмотрены в [5, 6].

Поскольку мощность, выделяющаяся в теле i, расходуется на его нагрев и передается окружающим телам (Т–Т), теплоносителям (Т–Ж) и средам (Т–СР), то уравнение теплового баланса для твердых тел, теплоносителя и среды имеет вид

NT qT = CidT- + £ К* - T (T - j F," T + dt    j=1

N

Ж

+ Z K T " Ж ( T - T ) F l ^- Ж +             (4)

i = 1

N CP

+ZKT"CP (T - T) FT-CP, i = 1,..., NT к=1

где C_i ^T – полная теплоемкость тела i .

Тепловые потоки KT Ж (T -T) FT Ж , переданные от тела i к теплоносителю в объеме l (площадь контакта ftЖ), и мощность дЖ рас- ходуются на нагрев движущегося теплоносителя. Поэтому уравнения теплового баланса для потоков теплоносителей записываются в виде

NЖ чЖ + Z К- Ж (Ti - T) = С,Ж -T+с  G, (t,вых - T-х), (5)

I = 1                                 ^-t                                V )

l = 1,..., Nж где первое слагаемое в правой части соответствует тепловому потоку, идущему на изменение температуры теплоносителя в объеме l с полной теплоемкостью ClЖ , а второе – тепловому потоку, выносимому из объема при прохождении теплоносителя с массовым расходом Gl . Для газов, как правило, первое слагаемое пренебрежимо мало в большинстве систем охлаждения.

Теплоноситель в объеме l может поступать из других объемов (m = 1,...,Nж, m ^ l) и из сред с известной температурой (k = 1,...,NCP), т. е. на входе в l-ый объем может происходить смешение потоков теплоносителей с температурами Tlвых и TkCP . Тогда температура Tlвх рас- считывается из следующего соотношения: NЖ               NCP

С]vdGh вх = Ус iGmh вых + Уек"’GTCP; l ll        m mll         k klk m=1                  k=1

NN ЖCP

Gi =z Gmi +z Gki, l = 1,..., Nж m=1

Для замыкания системы ( N_T + 2 N_ж ) уравнений (4) – (6) с неизвестными температурами T i ( i = 1,..., N T ) , T l , T| ^bx , ^ вых ( l = 1,..., N_ж )

следует добавить соотношения, связывающие температуру T_l с температурами T_l ^вх , T_l ^вых . Так, например, в случае замкнутой системы с подключенным к теплообменнику термостатом, мощность которого определяется температурой входящего в него теплоносителя, замыкающим будет уравнение изменения во времени температуры выходящего из термостата потока, вида:

вх вых          l

^T = T i  ± Т^ Ж Т Ж

GlCl

где W – выходная мощность термостата.

Таким образом, модель системы тел и потоков теплоносителей описывается системой ( N_T + N_ж ) обыкновенных дифференциальных уравнений (4), (5) и 2 N_Ж алгебраических уравнений (6) и (7), содержащих искомые температуры T_i , T_l , T_l ^вх , T_l ^вых . Для полной постановки задачи задаются значения температур в начальный момент

T i l= 0 = T i о ; T i l= o = T i о               (8)

Рассмотрим построение тепловой модели с сосредоточенными параметрами для испытательной системы, включающей в себя полый аппарат кубической формы (блок 4) объемом 3 м3, содержащий поверочную газовую среду (блок 6) и снабженный теплообменником (блок 3), в который подается теплоноситель (блок 2) из термостата (блок 1). Моделью учитывается распространение теплоты в окружающую среду (блок 5). Тепловая схема системы приведена на рисунке 1.

Для математического описания процесса теплообмена между потоком теплоносителя и теплообменным оборудованием, будем считать, что трубная часть аппарата разбивается на N элементов.

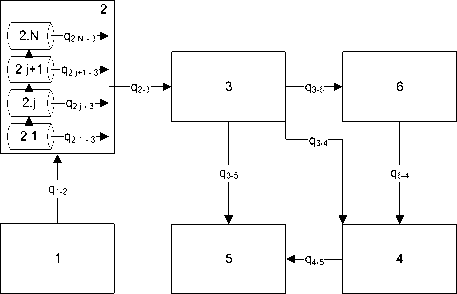
Рисунок 1. Тепловая блок-схема технологической системы, где q – тепловые потоки между элементами системы

Figure 1. The thermal block diagram of the technological system, where q – heat fluxes between the elements of the system

Элементы тепловой схемы связаны следующими потоками: q₁₂ = ± W ( t_2N , T _2l1m) - тепло-

вой поток от термостата, Вт, где W – выходная

мощность термостата,

2 lim

температура

= т1; к 3 (У ^а Ж ) + r 2 - 3

k,. = ------ ¹------

( V ^а СР ) ⁺ r 3 - 6

; ^K 3 - 5

r 3 - 5

^K 4 - 5

1;

(У ^а СР ) + r 4 - 5

термостатирования, K, T _{2 N} – температура теплоносителя на выходе из теплообменника, K;

N q2-3 = ^ q2i - суммарный тепловой поток i=1

между элементами теплоносителя и теплообменным оборудованием, Вт; q _{3 - 4} - тепловой поток между корпусом теплообменного оборудования и корпусом аппарата, Вт; q _{3 - 5} - тепловой поток между корпусом теплообменного оборудования и окружающей средой, Вт; q _{3 - 6} - тепловой поток между корпусом теплообменного оборудования и средой в аппарате, Вт; q ₄ _ ₅ -тепловой поток между корпусом аппарата и окружающей средой, Вт; q ₆ _ ₄ - тепловой поток между средой в аппарате и корпусом аппарата, Вт.

Выражения для оценки тепловых потоков имеют вид:

6-4 (V а СР ) + Гб-4, где аЖ - коэффициент теплоотдачи от жидкости к стенке в трубном пространстве, Вт / (м2·К); аСР - коэффициент теплоотдачи от газа к стенке с замкнутом объеме, Вт / (м2×К), r – термическое сопротивление стенки между элементами тепловой схемы, м2 × К / Вт.

Величина коэффициента теплоотдачи от газа к стенке в замкнутом объеме рассчитывается по уравнению:

а _СР = 9,74 + 0,07 -A Т        (10)

где A Т - разность температур стенки и газа, °C.

Величина коэффициента теплоотдачи жидкости оценивается по соотношению:

^а ж =

Nu - X

l

' q i - ₂ =± W(T ₂ N ,T _zlim )

q 2-3 =fq2i-3 =^k 2-3 (T3 - tj q3-4 = K3-4 (T3 - T4 )F3-4

q 3 - 5 = к 3 - 5 (T 3 - T 5 )F 3 - 5

q 3 - 6 = K 3 - 6 (T 3 - Т б )F 3 - 6

q4-5 = K4-5 (T4 - T5 .F, q6-4 = K6-4 (T6 - T4 )F6-4

где Nu - критерий Нуссельта, X - теплопроводность жидкости, Вт/(м×К), l – характерный размер, м.

Величина критерия Нуссельта оценивается в соответствии с рекомендациями в зависимости от условий движения теплоносителя в трубном пространстве теплообменного оборудования.

Уравнение теплового баланса для данной схемы имеет вид:

q 2 j   q 2j-1 q 2 j +1 q 2 j - 3 , J 1, N q 2 j-1 = g2 c2 (T2 j-1 - T2j

_ q 2 . + 1 = g 2 c 2 T . + 1 - T 2 j

dT 2.

С2    ,      q 2.J-1   q 2.j+1   q 2.j- 3, dt

dT 3

^C 3 ,      q 2 - 3 q 3 - 4    q 3 - 5 q 3 - 6

dt

^C 6  ,, = q 3 - 6    q 6 - 4

j = 1, N

где ^q _2j - 1 , ^q ₂ . j , ^q _{2j +} i - тепловые потоки между элементами теплоносителя, Вт; т ₃ + Т ₆ - температура соответствующего блока схемы, K; G ₂ - расход теплоносителя, кг/с; C ₂ = Cp ₂ m ₂ -теплоемкость теплоносителя, Дж/К; K _{2 - 3} , K _{3 - 4} , K _{3 - 5} , K _{3 - 6} , K _{4 - 5} , K _{6 - 4} - коэффициенты теплопередачи между блоками тепловой схемы, Вт /(м 2 ^К); F 2 - 3 , F 3 - 4 , F 3 - 5 , F 3 - 6 , F 4 - 5 , F 6 - 4 ^- поверхности теплопередачи между блоками тепловой схемы, м².

Коэффициенты теплопередачи рассчитываются по следующим выражениям:

dT

^C 4^r= q 3 - 4 ⁺ q 6 - 4 ^- q 4 - 5 dt

C 5 dT 5= 0 dt

T               ₊ W ( T 2N , ^T 2lim ) (

^T 2.1 ⁽ t ) = ^{T (} t L N ±----777----- ⁽ пРи t > ⁰ )

G ₂ C ₂

Начальные условия

• ^T 2.1.. N |t = 0 = ^T 20^{; T} 3 | t = 0 = ^T 30^{; T} 6 | t = 0 = ^T 60^;

• ^T 4 1 1 = 0 = ^T 4 0 ; ^T 5 1 1 = 0 = ^T 5 0

где C i = Cp i m i , i = 2...6 - теплоемкости блоков тепловой схемы, Дж/К; W ( Т ₂ N , Т _{2 lim} ) - мощность термостата по нагреву или охлаждению, Вт;

T ₂₀ – температура теплоносителя на входе в теплообменное оборудование в начальный момент времени, К.

Для решения системы дифференциальных уравнений первого порядка (2), которые в общем виде представляется выражением

— = f ( t , T ); 0 <  t <  t kOH .         (13)

dt с заданными начальными, использовался методом Рунге-Кутта.

При численном решении данной задачи область непрерывного изменения аргумента 0 < t < tKOH заменяется дискретным множеством {tj}J=1, называемым временной сеткой. В случае равномерной сетки шаг по времени постоянен: At = tj+1 - tj = const и tj. = jAt, j = 1,..., J. Вместо задачи определения непрерывной функции T(t) решается задача определения дискретного множества значения функции Tj = T(tj) в узлах сетки.

Схема Рунге-Кутта строится на основе аппроксимации следующего вырожения на tj +1

j - T j = i f ( t , T ( t )) dt ⁽¹⁴⁾ t j

В схеме Рунге-Кутта второго порядка точности интеграл рассчитывается на основе значения функции f в точках tj. и tj.+1, а приближенное значение uj+1 - uj = [f(tj, uj)+ f(tj+1, u(1))]At / 2, (15) где u(1) = uj +At x f (tj, uj).

Схема Рунге-Кутта позволяет определить искомое значение сеточной функции U j _{+ 1} на основе известного значения u _j и является явной схемой. Явная схема Рунге-Кутта устойчива для рассматриваемых систем.

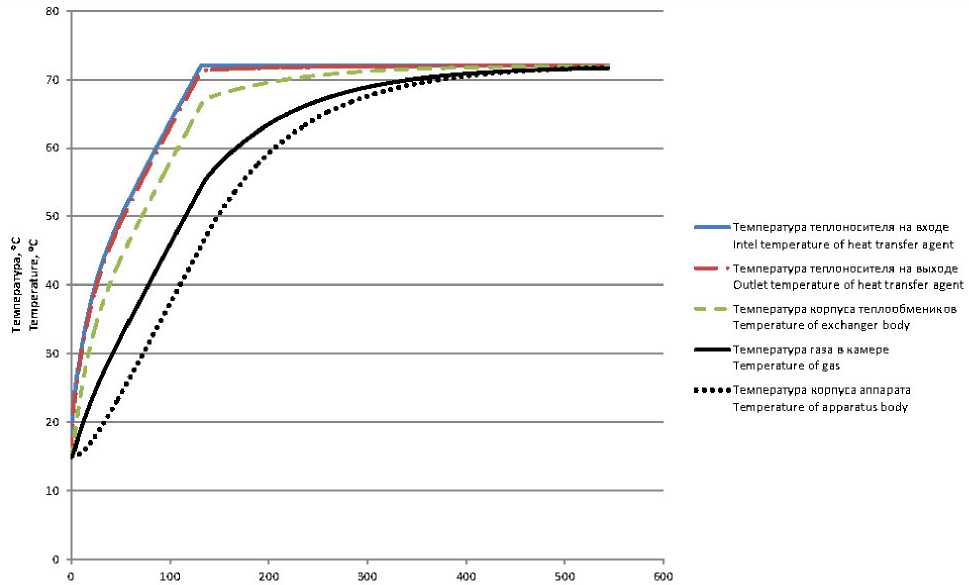
На рисунках 2, 3 представлены зависимости изменения температуры от времени в нестационарном режиме термостатирования полого аппарата кубической формы; температуры теплоносителя на входе и выходе, температуры корпуса теплообменников, температуры газа в камере, температуры корпуса аппарата.

отрезке [ t j , tj + 1 ] :

Время, мин.

Time, min.

Рисунок 2. Зависимость изменения температуры от времени в нестационарном режиме термостатирования при нагреве аппарата

Figure 2. The dependence of temperature changes on time in unsteady thermostating mode when the apparatus is heated

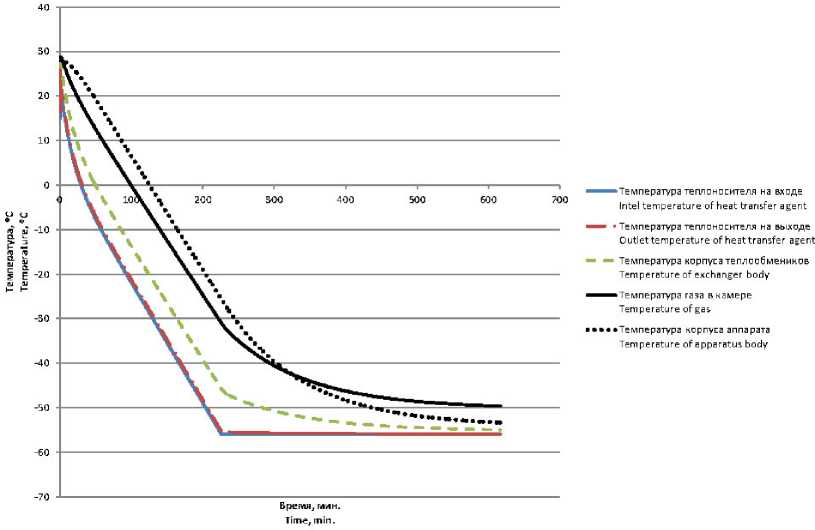
Рисунок 3. Зависимость изменения температуры от времени в нестационарном режиме термостатирования при охлаждении аппарата

Figure 3. Dependence of temperature change on time in unsteady temperature control mode when the device is cooling

Заключение

На основе метода поэтапного моделирования разработана математическая модель с сосредоточенными параметрами, позволяющая оценить средние температуры в системе тел и потоков теплоносителей, находящихся во взаимном теплообмене в технологической системе на этапе проектирования. Математическая модель, представляет собой систему обыкновенных дифференциальных уравнений, для решения которой использован явный метод Рунге-Кутта.

Получены зависимости изменения температуры от времени для двух нестационарных режимов термостатирования полого аппарата кубической формы, снабженного теплообменником, в который подается теплоноситель. В результате исследования получено, что время выхода на режим термостатирования при охлаждении до минус 70 ° С - 680 мин; при нагревании до 50 ° С - 550 мин. Результаты математического моделирования были использованы при разработке конструкторской документации на технологическое оборудование испытательной системы.