Разработка математических моделей технологического оборудования поворотного лесопогрузчика в режиме подъема груза

Введение. В лесной промышленности широко применяются машины, у которых в качестве рабочего оборудования установлены комбинированные гидрофицированные манипуляторы. Машины такого типа используются на следующих операциях лесозаготовительного производства: валка, валка-пакетирование, подбор и трелевка ранее поваленных деревьев, штабелевка сортиментов, подача деревьев к сучкорезным устройствам, погрузка сортиментов и т.д. Кроме этого они выполняют различные вспомогательные работы: погрузка и выгрузка стройматериалов (сыпучих грузов) при строительстве дорог, укладка плит на полотно дороги, погрузка пневого осмола, уборка отходов на нижних складах и другие работы. Лесопогрузчики поворотного типа находят широкое применение в лесной промышленности при заготовке древесного сырья в виде сортиментов и хлыстов. Работы по созданию и совершенствованию лесных машин целесообразно проводить на основе изучения динамики элементов конструкции и рабочих режимов. При этом методы математического моделирования являются наиболее эффективными. Исходя из этого, исследования на математических моделях динамики режима движения технологического оборудования с грузом поворотного лесопогрузчика, направленные на обоснование параметров кинематики и конструкции технологического оборудования, следует считать актуальными.

Обоснование расчетной схемы

Расчетная схема системы «технологическое оборудование – груз» представлена на рисунке 1. Рассматриваемый режим может иметь место при работе манипулятора в качестве технологического оборудования лесопогрузчиков, валочно-трелевочных машин, машин для бесчокерной трелевки деревьев и других лесосечных и дорожно-строительных машин.

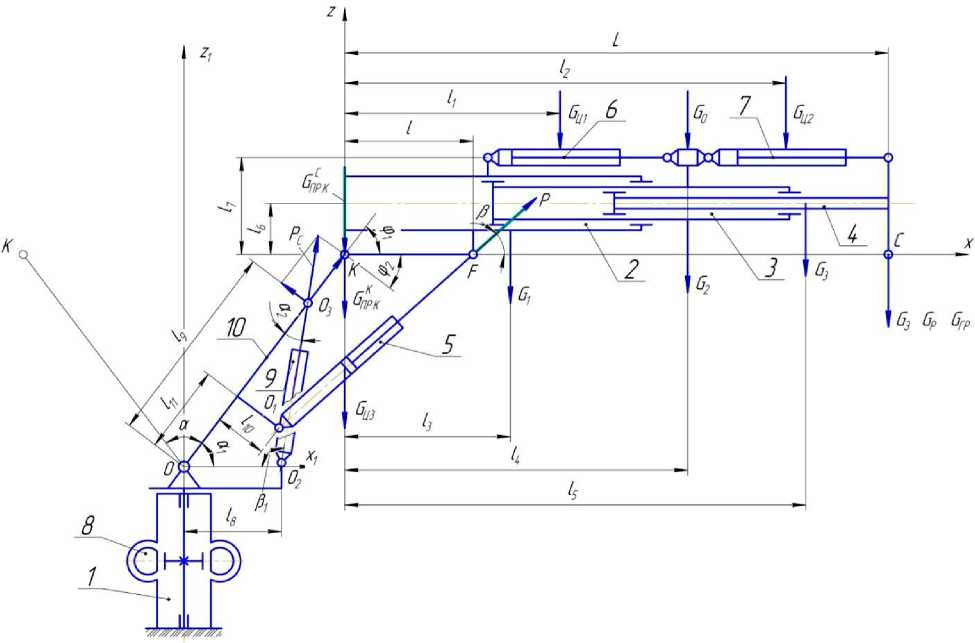
Рис. 1. Расчетная схема системы «технологическое оборудование – груз» (манипулятор с отклоняющейся колонной): 1 – опорно-поворотное устройство; 2–4 – наружная, средняя, внутренняя секции телескопической стрелы; 5 – гидроцилиндр подъема стрелы; 6, 7 – гидроцилиндры МВС;

8 – механизм поворота манипулятора в горизонтальной плоскости; 9 – гидроцилиндр поворота колонны;

10 – колонна; О 1 K = С; ОО 2 = ℓ 8 = C 1

После захвата груза рабочим органом он подтягивается к машине телескопической стрелой втягиванием секций, затем включением гидроцилиндров поворота колонны (МПК) и подъема стрелы (МПС) груз устанавливается в транспортное положение. При этом стрела совершает поворот относительно оси K, а колонна относительно оси О. Угол поворота стрелы φ (относительное движение), угол поворота колонны α (переносное движение). Отсчет начала угла φ от крайнего нижнего положения стрелы; отсчет угла α – от крайнего правого положения колонны.

На рисунке 1 приняты следующие обозначения:

G 1 , G 2 ,G 3 – силы тяжести наружной, средней и внутренней секций стрелы;

G Ц1 ,G Ц2 , G 0 – силы тяжести гидроцилиндров выдвижения секций и механизма выдвижения секций стрелы;

G З , G ГР , G Р – силы тяжести захвата, груза, ротатора;

G Ц3 , G Ц4 – силы тяжести гидроцилиндров поворота колонны и подъема стрелы;

G ПР.С – суммарная сила тяжести элементов конструкции стрелы и груза, приведенная к точке С;

Р, Р С – усилия на штоках гидроцилиндров поворота колонны и подъема стрелы;

L – размер стрелы при втянутых секциях;

ℓ 1 , ℓ 2 , ℓ 3 , ℓ 4 , ℓ 5 – расстояния от оси вращения стрелы K до центров тяжести элементов конструкции; ℓ 6 , ℓ 7 , ℓ 8 , ℓ 9 , ℓ 10 , ℓ 11 – размеры элементов конструкции манипулятора.

Разработка уравнений движения системы «технологическое оборудование – груз»

Стрела совершает вращение в плоскости ZKX, колонна – в плоскости Z 1 OX 1 . Углы поворота α и φ однозначно определяют положения данных элементов системы в плоскостях вращения. При известных размерах стрелы L и колонны L K положение любой точки может быть определено через указанные параметры.

Исходя из этого, систему можно рассматривать как систему с двумя степенями свободы (K = 2) с обобщенными координатами α и φ.

Для составления уравнений движения данной механической системы воспользуемся уравнениями Лагранжа 2-го рода. В соответствии с числом степеней свободы системы записываем два уравнения Лагранжа

Ш—(Э = « • • Х)-(Э =

где Q _a, Q ^ - обобщенные силы, соответствующие обобщенным координатама и ф соответственно.

Кинетическая энергия рассматриваемой системы равна сумме кинетических энергий колонны и стрелы, т.е. сумме кинетических энергий в относительном и переносном движении

T = Т 1 + T 2 ,                                                 (2)

где T 1 – кинетическая энергия приведенной массы колонны вместе с приведенными массами элементов конструкции, смонтированных на ней (гидроцилиндров поворота колонны и подъема стрелы и других частей гидропривода);

T 2 – кинетическая энергия приведенной массы стрелы и груза.

В процессе поворота телескопической стрелы ее секции не выдвигаются, размер стрелы L не изменяется, следовательно, положения центров масс элементов конструкции стрелы относительно оси K (радиусы инерции масс) остаются постоянными. В этом случае с целью упрощения определения кинетической энергии системы массы элементов конструкции телескопической стрелы приводим к точке C – к точке подвеса ротатора к стреле. Массу элементов конструкции колонны приводим к оси крепления стрелы K. При определении приведенной массы элементов конструкции стрелы m ПР.С исходим из условия равенства кинетической энергии приведенной массы сумме кинетических энергий масс, которые она заменяет.

Следовательно

—С⁷— = 77 • [(^ 1 ¹ 2 ⁺ ^ 2 ¹ 2 + ^ з ¹ 2 + ^G ц 1 ¹ 2 + G_o ^{1 2} + G p + G з + G rp )].     (3)

2д 2д

Отсюда приведенная к точке C масса стрелы

Или

^т ПР . С

^G np . С _ ^G 1 д д

р2 г р2 Г 22 Г 22

• ¹ з ₊ _ 2 . ^{1 4} ₊ _ з • ^{1 5} ₊ ^G Ц 1 • ¹ 1

L ²    д  L ²     д  L ²     д   L ²

I П о ¹ 2

+7 7^ +

G p +G з + G гр

^G Ц 2 д

L^{2 +}

^т пр . с ^_т 1Г 2 ^{+ т} 2Г Г ^{+ т} зг 2 ^{+ т} Ц 1^ 2 ^{+ т} Ц 2^ 2 ^{+ т} о г т ^{+ т} р ^{+ т} з ^{+ т} гр • ⁽⁵⁾

где m 1 – масса наружной секции стрелы;

• m 2 – масса средней секции стрелы;

• m 3 – масса внутренней секции стрелы;

• m Ц1 , m Ц2 – массы гидроцилиндров механизма выдвижения секций;

• m 0 – масса механизма выдвижения секций;

• m Р , m З , m ГР – массы ротатора, захвата, груза.

Приведенная к точке K масса колонны и элементов конструкции, закрепленных на ней может быть определена из следующего выражения:

G ПР . К а² 4 _ G К a² (0,5L К )² + 0,5G ц ₃ а:² (0,5 1 )² + 0,5G ц ₄а² (0,5 1 ₈ )² 2д            2д              2д                2д '

При составлении выражения (6) исходим из допущения о том, что силы тяжести гидроцилиндров GЦ3 и GЦ4 равномерно распределены между стрелой и колонной, а так же между колонной и основанием опорно- поворотного устройства; точки их приложения находятся, соответственно, 0,5ℓ и 0,5ℓ8 от оси крепления стрелы к колонне – точка K.

Из выражения (6) приведенная к точке K масса колонны и элементов конструкции равна

Gк  (0,5Lк)2    0,5Gц3   (0,51)2    0,5Gц4 (0,5Lк)2           Gк    „ .^Gц3   12  ,      1 nr        12

• mПР.К = — ■—2— + —— •-^ +---—2---= 0,25у + o,125— •-T ++0,125mц4 ■-2,(7)

• 9     L к        9      L к          9L к              9           9   L к              LL

или mПРк = 0,25 mк + 0,125mц3 ■ — + 0,125mц4 ■ l|.

.                                         L К

В соответствии с (2) кинетическая энергия системы

Т = Ti + Т2 =   " + 2 (mпрс ]£ + Io ф2} ,(9)

где    I₀ - момент инерции колонны относительно оси О;

• 1 _С - центральный момент инерции стрелы в сборе;

У ас - скорость абсолютного движения точки С - точки приведения массы стрелы.

Применим теорему о сложении скоростей, в соответствии с которой абсолютная скорость точки С равна геометрической сумме ее переносной и относительной скоростей:

Уа2с = Уе2 + Vr2c + 2Уес ■ Угс cos у, где   Уес , Vrc - скорости переносного и относительного движения точки С;

• у - угол между направлениями векторов переносного и относительного движения точки С.

На рисунке 2 показана схема для определения скорости абсолютного движения точки С - У ас - точки приведения массы стрелы и груза.

У ес = ОС ■а. ; У_гс = L ■ ф .

Из треугольника ОКС

ОС ² = L 2 K + L ² — 2L к ■ L cos(ф_н + ф) .

Из этого же треугольника L ^ = L² + ОС ² — 2L^ ОС■ cos С .

Из рисунка 2 следует, что углы у и С равны, как углы со взаимно перпендикулярными сторонами. Следовательно, cos С = cos у =

l² + ос ² -С К

2L*OC .

Скорость абсолютного движения

У_а ² = а² ■ ОС ² + ф² ■ L ² + 2а ■ ф ■ L^ ОС ■ cos у.

Выразим cos у = cos С через cos(ф _Н + ф) .

L2 + ОС —Lm L2 + L +L2 —2L« ■L■COS(ф|-|+ф)—L2 L2 —L/cLI4

cos у = -------- К =---- К------к-----Н—¹-—- =1----— I ■ cos(ф_н + ф) .

• ’       2L^OC                   2L^OC               L L-OC J

После подстановки получим:

• Уа2 = а2 ■ ОС2 + ф2 ■ L2 + 2а ■ ф ■ L ■ ОС ■ [L—-—| ■ cos(фн + ф).(10)

L L^OC

С учетом (10) выражение кинетической энергии принимает вид

Т =

^m пр . к -L^a² + m пр ,_с-ОС²-а² ^ ш пр .с^Ф² 2                2                2

[ ^LrOC ⁱ]'^ras(^ ⁺ ф ⁾⁺ '-^

+ m _ПР . с • L • ОС • а • ф •

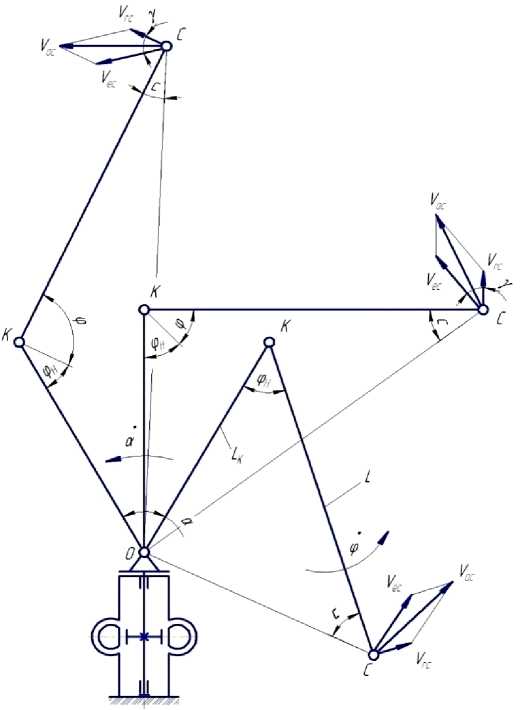
Рис. 2. Схема для определения скорости абсолютного движения точки С при одновременном движении стрелы и колонны: φ н – начальный угол между осями стрелы и колонны; φ – угол поворота стрелы (относительное движение); а - угол поворота колонны (переносное движение); а, ф - угловые скорости колонны и стрелы

Разработка моделей движения системы «технологическое оборудование – груз»

Комбинированными манипуляторами с отклоняющимися колоннами и телескопическими стрелами оснащаются машины для заготовки древесного сырья в виде сортиментов (форвардеры, харвестеры, машины для штабелевки сортиментов, лесопогрузчики). Для погрузки хлыстов и деревьев с кроной с помощью таких машин требуются специальные захваты с устройствами для устранения явления «кострения» деревьев. Такие захваты для оснащения лесопогрузчиков с комбинированными манипуляторами не выпускаются, что затрудняет использование их на погрузке длинномерного древесного сырья. Исходя из этого, при составлении уравнений движения рассматриваемой системы упругие и демпфирующие свойства груза не учитываем.

Дифференцируя выражение кинетической энергии (11) по составляющим уравнений Лагранжа (1), по- лучаем уравнение движение в следующем виде:

4L 2 -L K 1L1 ^ф [ L-ОС \

• соз(ф н + ф} -

^m пр . к ' ^L K' ^а + ^m пр . с . ' ОС 2 ' ^а + ^m пр . С ' ^ОС ' ^L'

-т пр . с ■ ОС • L - ф² • [ ^LoCr ] • 5т(ф н + ф ^} = Q a .

(т пр . с I? + 1 с ^} ф + т пр . с ■ ОС • «• ^L • [^ ОССт ] • ^со5( ф н ⁺ ф ^} = ^Q ^ ^.

Определение обобщенных сил Qф и Qa, соответствующих обобщенным координатам системы ф и а

Для определения обобщенных сил Q φ и Q α воспользуемся принципом возможных перемещений системы в направлении возрастания обобщенных координат ф и а - Др и Да . При этом при вычислении обобщенной силы Q ф принимаем Да = 0, а при вычислении Q а Д(р = 0. В качестве активных сил принимаются силы тяжести элементов конструкции и груза G i , усилия на штоках гидроцилиндров Р С и Р . Обобщенная сила принимается в виде коэффициента в выражении суммы элементарных работ активных сил в направлении возможного перемещения:

5 А _v = Q_v • Д ф ; 5 А _а = Q_a • Д а.

Определим сумму элементарных работ активных сил в направлении обобщенной координаты φ. При этом Др Ф 0, Да = 0.

При определении обобщенной силы Q φ используем выражения (4), (5) приведенной к точке С массы стрелы m пр.с при горизонтальном положении стрелы. Тогда £ 5 А ^ = ( Р1 sin р —т _ПР . С gL) Др .

Q_v = Р1 sin р-т _Пр . с gL .

Определим сумму элементарных работ активных сил и сил тяжести элементов конструкции в направлении обобщенной координаты а. При этом Др = 0; Д а / 0 . В направлении обобщенной координаты а совершают работу активная сила Р С и силы тяжести элементов конструкции стрелы и колонны. С целью упрощения выражения обобщенной силы Q α приведем силы тяжести элементов конструкции стрелы, груза и колонны к точке K. При этом рассматриваем горизонтальное положение стрелы. Приведение сил к выбранным точкам выполняем исходя из условия равенства моментов приведенной силы сумме моментов приводимых сил относительно любой точки на плоскости (теорема Вариньона).

При определении приведенной к точке K силы тяжести стрелы используем выражения приведенной массы стрелы к точке С при горизонтальном положении стрелы (4), (5) m ПР.С .

Составим уравнение моментов приведенной силы тяжести стрелы к точке С G _ПР . С и приведенной силы тяжести стрелы к точке К - G ^ . К относительно оси О.

Отсюда G ПР . К

т пр . с g ⁽ L + L_K . cos aj = G Пр . _K • L_K . cos а 1 .

m n_Pr g(L+L_K . cosa-i) m пр . c gL+m пр . c gL_K . cosa -

Li p cosa 1

L_K cosa 1

. m пр . c gL

L_K . cosa 1

+ ^т ПР . С ^g .

Определим приведенную к точке К силу тяжести элементов конструкции колонны и гидроцилиндров привода исполнительных механизмов G C , G Ц4 , G Ц3 . При этом воспользуемся выражениями (7), (8) определения приведенной массы указанных элементов конструкции к точке K:

^G Пр . к = ^т пр . к g .                                          ⁽¹⁶⁾

Тогда £ 5 А _a = [ Р с • sin а₂ • 1 ₉ - ( G ПР . к + G ПР . к )L_K . cos а 1] Да .

^Q a = Рс ^{sin а} 2 • ¹ 9 ^— ( ^G пр . к ^{+ G} пр . К } ^LK - ^{cos а} 1 ^.

Так как переносное движение системы является вращательным и при одновременном вращении колонны и стрелы расстояние ОС (рис. 3) постоянно возрастает, возникает поворотное (кориолисово) ускорение ω С и кориолисова сила инерции F C .

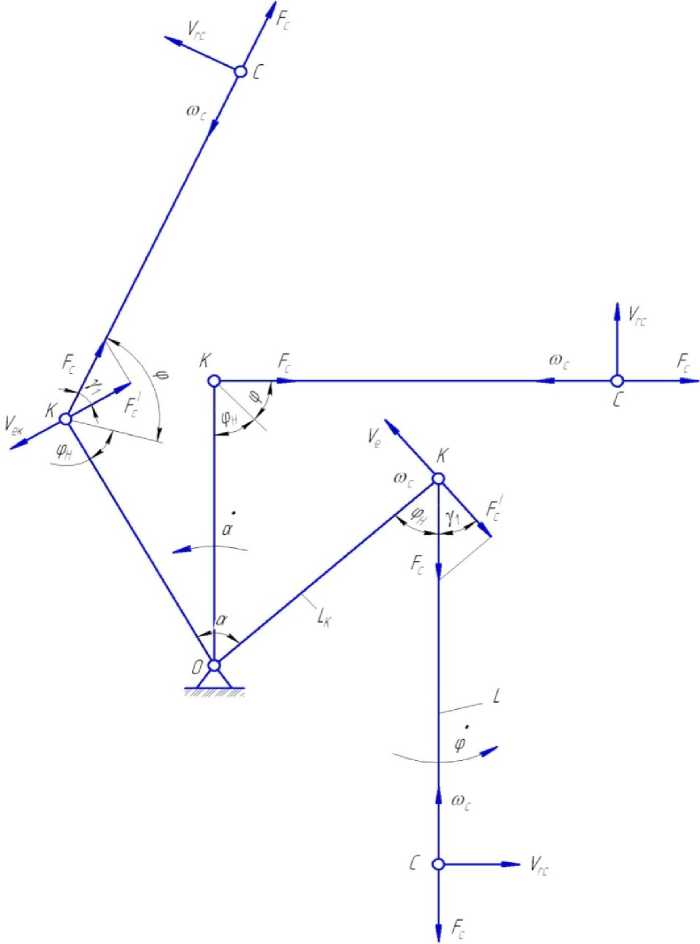
Рис. 3. Схема для определения ускорения кориолиса и кориолисовой силы инерции: ω С – кориолисово ускорение; F C – кориолисова сила инерции; V ℓc, V rc – линейные скорости переносного и относительного движения точки С

Кориолисово ускорение определяется по формуле

а) с = 2d -V_rc = 2d • ф • L .

С учетом момента от кориолисовой силы инерции обобщенная сила принимает вид

Q_a = Рс- sin d 2 • 1 ₉ - ( G ПКр . к + С С . к )L_K • cos d i - 2m _Пр . c -d -ф -L-L _K ■ cos / i . (17)

С учетом выражений (14) и (17) уравнения движения рассматриваемой динамической системы принимают следующий вид:

^т пр . К ’ ^L K • а + ^т пр . с . • ОС ² • а + т пр . с • ОС ■ L- ^ф

'L² - L К -L L^OC

• cos ⁽ ф н + ф) -

L ² - L К •L

— т пр . с ■ ОС^ L^ ф² ■            • sin ⁽ ф н + ф) =

L • ОС

= Р с • sin а₂ • 1 ₉

-

( G Пр . к + G Ср . к )L_K . cos a i - 2т пр . с •а •ф -L^L к ■ cos Y i .

(т пр . с L² + 1 с )ф + т пр . _с ■ ОС • a-L-^ ^^^- ]• cos ⁽ ф н + ф) = Р1 sin 0-т пр . _с gL.      (18)

Заключение. В результате выполненной работы получена система неоднородных дифференциальных уравнений второго порядка, являющихся основой математических моделей лесопогрузчиков поворотного типа при работе в режиме подъема груза. Из уравнений следует, что состояние нагруженности элементов конструкции лесопогрузчика зависит от ряда конструктивных и эксплуатационных факторов.