Разработка математической модели кинетики процесса дегидрирования этилбензола в двухступенчатом адиабатическом реакторе непрерывного действия
Автор: Битюков В.К., Жатова И.А., Алексеев М.В., Попов А.П.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Информационные технологии, моделирование и управление
Статья в выпуске: 2 (64), 2015 года.
Бесплатный доступ
Статья посвящена математическому моделированию кинетики процесса дегидрирования этилбензола в двухступенчатом адиабатическом реакторе с каталитическим слоем, функционирующим по непрерывной технологии. Проведен анализ химических реакций, протекающих параллельно основной реакции образования стирола, исходя из чего сделан ряд предположений, на базе которых составлена кинетическая схема, описывающая механизм протекания химических превращений во время процесса дегидрирования. Разработана математическая модель процесса дегидрирования, описывающая динамику химических реакций, протекающих в каждой из двух ступеней реакторного блока при постоянной температуре. Выполнена оценка констант скоростей прямых и обратных реакций образования и исчерпывания каждого компонента прореагировавшей смеси. Получена динамика изменения концентрации исходного вещества (этилбензольной шихты), динамика образования стирола, а также всех побочных продуктов дегидрирования (бензола, толуола, этилена, углерода, водорода и др.). Рассчитанные изменения компонентного состава реакционной смеси за время её прохождения через первую и вторую ступени реактора показали, что предложенное математическое описание адекватно воспроизводит кинетику исследуемого процесса. Это доказывает преимущество созданной модели, а также верность найденных значений констант скоростей реакций, что предоставляет возможность использования модели для расчета кинетики дегидрирования этилбензола при неизотермическом режиме его проведения с целью определения оптимальной траектории изменения температурного режима работы реактора. В дальнейшем это позволит снизить энерго- и ресурсозатраты, увеличить количество произведенного стирола и повысить экономические показатели процесса.
Дегидрирование этилбензола, адиабатический реактор, химическая кинетика, математическая модель, константа скорости реакции
Короткий адрес: https://sciup.org/14040437
IDR: 14040437 | УДК: 66.011
Текст научной статьи Разработка математической модели кинетики процесса дегидрирования этилбензола в двухступенчатом адиабатическом реакторе непрерывного действия
Алексеев М.В., Попов А.П., 2015
Стирол является одним из важнейших продуктов нефтехимии и сырьем для производства полимерных материалов.
В настоящее время основным промышленным способом производства стирола в России является каталитическое дегидрирование этилбензола.
Основной стадией рассматриваемого процесса является отделение молекулы водорода от поступающей в реактор этилбензольной шихты, так как именно на этой стадии образуется конечный продукт – стирол. Поэтому на сегодняшний день актуальна задача интенсификации этой производственной стадии, которая может быть осуществлена следующими способами:
-
1. Модернизация используемых каталитических систем и разработка принципиально новых ускорителей данной реакции.
-
2. Усовершенствование АСУ процесса.
-
3. Оптимизация режима работы процесса c использованием методов математического моделирования (уменьшение расхода сырья, греющего пара, топливного газа, продление срока службы работы каталитической системы и др.).
Проведение подобных исследований и усовершенствований в промышленных и лабораторных условиях требует длительного времени, сложной химической, технической и программной работы, а также существенных капитальных затрат.
В условиях ограниченности сырьевых, финансовых, временных и производственных ресурсов 3-й путь является наиболее перспективным в случае его реализации с помощью методов математического моделирования и методов оптимизации. Так как это не требует затрат на техническую реализацию и позволяет сделать данный процесс менее ресурсо- и энергоёмким, а также увеличить процентное содержание производимого стирола в реакционной смеси на выходе из реактора.
На предприятии ОАО «Нижнекамскнефтехим» реакцию дегидрирования этилбензола проводят в адиабатическом двухступенчатом реакторе непрерывного действия (с каталитической зоной по длине каждой ступени) при температуре 560 oC на начальном этапе эксплуатации каталитической системы с повышением этого значения до 630 oC к окончанию её срока службы. В основном, дегидрирование осуществляется на железооксидных катализаторах, временной цикл работы которых составляет 2 года, после чего они подлежат замене [1].
Со временем (в процессе эксплуатации реактора) происходит снижение активности его каталитического слоя, что влечет за собой снижение конверсии этилбензола и одновременное падение процентного содержания стирола в реакционной смеси на выходе из ступеней реактора и соответственное увеличение содержания побочных продуктов Главной причиной падения активности катализатора является образование на его поверхности кокса.
Недостаток активности компенсируется увеличением температуры в реакторе, производимой на основе опыта операторов и без предварительного использования математического описания, позволяющего получить расчетные значения приращений по температуре ΔT и величины временных интервалов Δ t , через которые их необходимо производить. Данный фактор приводит к увеличению энерго- и ресурсозатратности данного производства, уменьшению количества произведенного стирола, снижению экономических показателей.
Исходя из всего изложенного, главная цель научного исследования - это разработка математического описания стадии дегидрирования, отражающего динамику изменения концентраций всех продуктов реакций в каждой ступени реактора для определения оптимальных путей управления этим процессом.
Решение поставленной задачи непосредственно связано с исследованием химической кинетики процесса дегидрирования, в том числе, и методом математического моделирования.
При моделировании использовалось математическое описание процесса, приведенное в работе [2]. В ходе выполнения научных исследований выявлено, что модель с приемлемой точностью описывает динамику изменения концентрации основных компонентов реакции на выходе из реакторного блока: этилбензола и стирола [3]. Но одновременно установлено несколько существенных недостатков данных математических описаний:
-
- завышение концентраций стирола и этилбензола на выходе из первой ступени реактора;
-
- высокая погрешность расчета концентраций побочных продуктов;
-
- не выполнение условий материального баланса процесса в обеих ступенях реактора;
-
- модель описывает процесс дегидрирования, который отличен от приведенного в технологическом регламенте ОАО «Нижнекамскнефтехим» [1]. Различия заключаются в представлениях о компонентном составе смеси на выходе из реактора.
Также необходимо отметить, что исходная модель [2] построена с учетом принятых допущений:
-
- при взаимодействии стирола и водорода происходит образование толуола, бензола, этилена и углерода;
-
- значения констант скоростей выхода продуктов мономолекулярных реакций равны;
-
- равенство констант скоростей прямых и обратных реакций.
Эти допущения снижают точность модели и сводят на нет возможность ее дальнейшего использования для исследования процесса.
В связи с этим, возникла необходимость усовершенствования модели и ее адаптации под условия рассматриваемого процесса.
Разработка математического описания процесса дегидрирования этилбензола осуществлялась путем использования кинетического подхода. Предварительно установлено, что реакция дегидрирования этилбензола на железооксидных катализаторах сопровождается побочными реакциями, выражающимися во взаимодействии продуктов реакций разложения этилбензола, которые могут приводить к образованию бензола, толуола, а также метана и углерода [4].
Исходя из вышеизложенного, получена кинетическая схема процесса, описывающая механизм реакции образования стирола и реакций выделения побочных продуктов дегидрирования, при создании которой приняты следующие допущения:
-
1) в результате взаимодействия образовавшихся молекул стирола с молекулами водорода происходит выделение толуола и углерода (бензол и этилен не образуются);
-
2) такие продукты реакции как бензол и этилен образуются только в результате реакции разложения этилбензола.
В течение процесса дегидрирования параллельно реакции отделения молекулы водорода от этилбензольной шихты происходит девять сложных химических реакций 1-го и 2-го порядков двух видов: мономолекулярные и бимолекулярные [5], некоторые из которых являются обратимыми. Исходя из этого, приняты два дополнительных допущения:
-
3) константы скоростей образования компонентов мономолекулярных, а также прямых и обратных реакций не равны;
-
4) значения констант скоростей образования компонентов бимолекулярных реакций, происходящих во время дегидрирования, одинаковы для каждой реакции.
В итоге (согласно принятым допущениям) кинетическая схема дегидрирования примет вид:
-
1. Реакция образования стирола и водорода: C 6 H 5 C 2 H 5 < — k 2 , k 3 > C 6 H 5 C 2 H 3 + H 2 .
-
2. Реакция образования бензола и этилена:
-
3. Реакция образования толуола и метана:
-
4. Реакция образования углерода и водорода:
-
5. Реакция образования углекислого газа и водорода:
-
6. Реакция образования угарного газа и водорода:
-
7. Реакция образования толуола и углерода в результате взаимодействия молекул стирола с молекулами водорода:
C 6 H 5 C 2 H 5 > C 6 H 6 + C 2 H 4 .
C 6 H 5 C 2 H 5 + H 2 "k > C 6 H 5 CH 3 + CH 4 .
CH 4 k 7 , k8 > C + 2 H 2.
C + 2 H2O ——9, —10 > CO. + 2 H2 .
CH 4 + H 2 O < k 11, k 1 2, — 13 > CO + 3 H 2 .
C6 H 5 C 2 H3 + 2 H 2 k14 > C6 H 5 CH3 + CH 4.
При разработке математической модели процесса дополнительно принят следующий ряд допущений:
-
1) Температурный режим работы реактора считается постоянным и равен 560 °С.
-
2) Изменение активности каталитической системы в течение процесса не учитывается.
-
3) Значения констант скоростей всех реакций считаются постоянными (следствие из допущения 1).
Таким образом, используя составленную кинетическую схему, получаем математическое описание процесса производства стирола для каждой ступени реакторного блока. Описание является теоретически обоснованной нестационарной кинетической моделью [6] и представляет собой систему дифференциальных уравнений, описывающих динамику изменения концентраций этилбензола и продуктов реакции в течении времени протекания процесса:
ас
- kC —3- CflCc - kMCaCc , (1)
1 b a c 14 a c dt k dC k
—— - — Ca C c - k 1 C b - k 2 C b - k 4 C b - k 5 C b , (2) dt kp
-
-=- - k 2 C b + k 8 C g + k 1o C h C1 , + k 12 C g C p - kk , — J3" C a C c — k 6 CbC c — J13 C m C c - k ,4 C ^ C C kp kp
dCf - k 4 C b , ( 4 )
dt dCT - k5 Cb, (5)
dt dC
—- = k 6 CC + k 14 CC -dt
dC g = k c c + _13 C C + k C C2 6 b c m c 14 a c dtk
—
, (7)
— k 7 C g — k 8 C g — k 11 C g C p
— k 12 C g C p
dC h = k 7 C g — k 9 C h C P dt
—
2 k 10 ChCp ,
dCk2
dt 9 h p , dCк
-m = k 11CgCp — -13 CCc , dtk
C a (0) = 0, C b (0) = 0.998,
C c (0) = C d (0) = 0.001,
C e (0) = C f (0) = C g (0) = 0,
Ch (0) = Ck (0) = Cm (0) = 0, где t – время прохождения слоя шихты через ступень реакторного блока, с; Ca, Cb, Cc, Cd, Ce, Cf, Cg, Ch, Ck, Cm – концентрации стирола, этилбензола, толуола, бензола, углерода, водорода, метана, этилена, угарного и углекислого газов соответственно, масс. доли; k1,k4 , k5, k7 - константы скоростей образования стирола, бензола, этилена и углерода соответственно, c-1; (k3 / kp) – константа скорости обратной реакции образования стирола, с-1/масс. доли; k6 – константа скорости образования толуола и метана, с-1/масс.доли; k2, k8 – константы скоростей образования водорода в реакциях 1 и 4, с-1; k9 – константа скорости образования углекислого газа, c-1/(масс.доли)2; k10 – константа скорости образования водорода в реакции 5, с-1/(масс.доли)2; k11 – константа скорости образования угарного газа, с-1/масс.доли; k12 – константа скорости образования водорода в реакции 6, с-1/масс.доли; (k13 / kp) – константа скорости обратной реакции взаимодействия метана с водяным паром, c-1/масс.доли; k14 – константа скорости образования толуола и метана при взаимодействии молекул стирола и водорода, с-1/(масс.доли)2; kp – константа равновесия, с-1.
Значения кинетических параметров модели, которыми являются константы скоростей происходящий реакций, кроме k p , неизвестны.
Константа равновесия рассчитывается для конкретного значения температуры реакции по следующей зависимости [2]:
kp = 16.72 • exp( — 15.35/ T ), (12)
где T – температура в реакторе дегидрирования, ° К . При T = 560 °C , k p = 16.429 с-1.
Оценка констант произведена с помощью численного метода оптимизации поиско- вого типа – метода Гаусса (покоординатного спуска) [7], по критерию минимума средней суммарной относительной погрешности концентраций компонентов после каждой ступени реакторного блока:
-
5 = (^Ca1 + - +5Cm1 + 5Ca 2 + "'+
+ 5C . )/(2 • N)— > min, (13)
Cm 2//V > k1, _ , k14 '
где ^ ^...,< ?c - относительные погрешности значений концентраций продуктов реакций после первой ступени реактора, рассчитанные по модели (1-11); ^ ,..., ^ - относительные
C a 2 C m 2
погрешности значений концентраций продуктов реакций после второй ступени реактора, рассчитанные по модели (1-11); N - количество компонентов реакционной смеси на выходе из первой и второй ступеней реактора ( N = 10).
На йденные в результате идентификации параметры k 1 ,..., k 14 представлены в таблицах 1, 2.
Т а б л и ц а 1
Значения констант скоростей мономолекулярных реакций
|
Наименование |
Величина константы скорости, с-1 |
|
k 1 |
0.267 |
|
k 2 |
0.0012 |
|
k 4 |
0.002 |
|
k 5 |
0.00116 |
|
k 7 |
12.331 |
|
k 8 |
0.400 |
Т а б л и ц а 2
Значения констант скоростей прямых и обратных бимолекулярных реакций
|
Наименование |
Величина константы скорости |
Размерность |
|
k 3 / k p |
0.013 |
с-1/масс.доли |
|
k 6 |
0.001 |
с-1/масс.доли |
|
k 9 |
9.3·10-3 |
c-1/(масс.доли)2 |
|
k 10 |
4·10-4 |
с-1/(масс.доли)2 |
|
k 11 |
0.190 |
с-1/масс.доли |
|
k 12 |
0.700 |
с-1/масс.доли |
|
k 13 / k p |
0.140 |
c-1/масс.доли |
|
k 14 |
15 |
c-1/(масс.доли)2 |
Расчет системы уравнений (1-11) выполнен для каждой из двух ступеней реактора с помощью численного метода Рунге-Кутта 4-го порядка. Итоговые значения концентраций продуктов дегидрирования этилбензола, полученные в результате расчета первой ступени реактора, являются исходными данными для моделирования процесса во второй ступени.
Результаты моделирования процесса дегидрирования слоя этилбензольной шихты за время её прохождения через каталитические зоны ступеней реактора представлены на рисунках 1-3 и в таблицах 3, 4.
Масс. доля
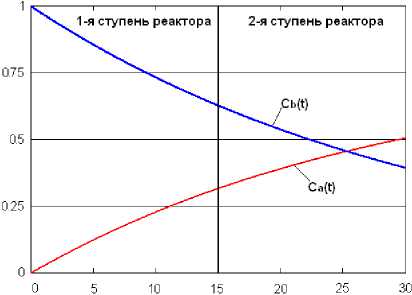
t, c
Рисунок 1. Динамика образования стирола и этилбензола за время прохождения шихты через 1-ю и 2-ю ступени реакторного блока
Масс. доля
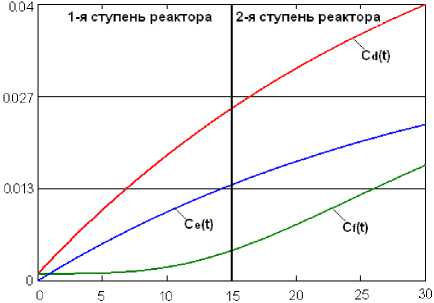
t, c
Рисунок 2. Динамика образования бензола, этилена и толуола за время прохождения шихты через 1-ю и 2-ю ступени реакторного блока
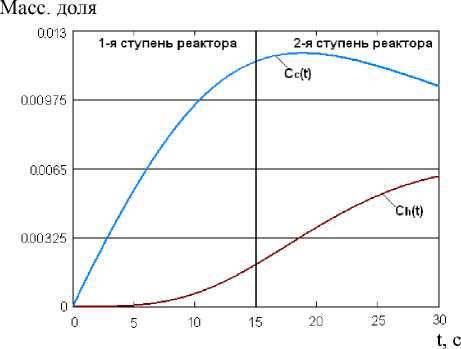
Рисунок 3. Динамика образования водорода и углерода за время прохождения шихты через 1-ю и 2-ю ступени реакторного блока
Т а б л и ц а 3
Состав реакционной смеси на выходе из первой ступени реактора
|
Концентрация основных продуктов реакции, % мас. |
Концентрация побочных продуктов реакции, % мас. |
Суммарная концентрация компонентов, % мас. |
||
|
Стирол |
31.623 |
Толуол |
0.436 |
2.929 |
|
Бензол |
2.493 |
|||
|
Этилбен зол |
62.631 |
Этилен |
1.388 |
1.587 |
|
Углерод |
0.199 |
|||
|
Метан |
4.1*10-3 |
1.235 |
||
|
Водород |
1.155 |
|||
|
Угарный газ |
0.012 |
|||
|
Углекислый газ |
0.064 |
|||
Т а б л и ц а 4
Состав реакционной смеси на выходе из второй ступени реактора
|
Концентрация основных продуктов реакции, % мас. |
Концентрация побочных продуктов реакции, % мас. |
Суммарная концентрация компо-нентов% мас. |
||
|
Стирол |
50.444 |
Толуол |
1.672 |
5.666 |
|
Бензол |
3.996 |
|||
|
Этилбензол |
39.308 |
Этилен |
2.259 |
2.873 |
|
Углерод |
0.614 |
|||
|
Метан |
5.3*10-3 |
1.715 |
||
|
Водород |
1.039 |
|||
|
Угарный газ |
0.058 |
|||
|
Углекислый газ |
0.613 |
|||
Согласно данным [1, 8, 9]:
-
1 ) на выходе из первой ступени реактора значения концентраций продуктов реакций находятся в следующих диапазонах:
-
- концентрация стирола 30-35 %;
-
- концентрация этилбензола 60-65 %;
-
- суммарная концентрация толуола и бензола не должна превышать 5 %;
-
- суммарная концентрация газов (H 2 , CH 4 , CO, CO 2 ) не более 1,5 %.
-
2 ) на выходе из реакторного блока (из второй ступени реактора) концентрации продуктов реакций находятся в следующих диапазоны:
-
- концентрация стирола 50-55 %;
-
- концентрация этилбензола 35-40 %;
-
- суммарная концентрация толуола и бензола не должна превышать 8 %;
-
- суммарная концентрация газов (H 2 , CH 4 , CO, CO 2 ) не более 2 %.
Анализ результатов моделирования показал количественное и качественное соответствие расчетных значений данным, приведенным в технологическом регламенте. Это свидетельствует об адекватности разработанной модели химической кинетики дегидрирования этилбензола, а также о правомерности выполненных оценок констант скоростей химических реакций процесса.
Разработанное математическое описание можно использовать для создания системы оптимального управления стадией дегидрирования в процессе производства стирола.
Список литературы Разработка математической модели кинетики процесса дегидрирования этилбензола в двухступенчатом адиабатическом реакторе непрерывного действия
- Технологический регламент производства стирола на ОАО “Нижнекамскнефтехим”, 1980.
- Островский Г.М., Волин Ю.М. Моделирование сложных химико-технологических схем. М.: Химия, 1975. С. 292-297.
- Алексеев М.В., Попов А.П., Жатова И.А. Разработка математической модели динамики дегидрирования этилбензола в производстве стирола//Сборник трудов XXVII международной научной конференции ММТТ-27.: в 12 т. Секция 9. Тамбов.: ТГТУ, 2014. Т.2. С.12.
- СтудопедиЯ. Производство бутадиена-1,3 дегидрированием н-бутана . Режим доступа: http://studopedia. ru/3_38394_proizvodstvo butadiena-degidrirova-niem-n-butana.html.
- Холохонова Л.И., Короткая Е.В. Кинетика химических реакций. Кемерово: КемТИПП, 2004. С. 4-11.
- Пушкарева Т.П., Перегудов А.В. Математическое моделирование химических процессов. Красноярск, 2013. С. 22-25.
- Васильев Ф.П. Методы оптимизации.-М.: Факториал Пресс, 2002. С. 310-316.
- Кирпичников П.А., Береснев В.В., Попова Л.М. Альбом технологических схем основных производств промышленности синтетического каучука. Л.: Химия, 1986. С. 98-100.
- Башкатов Т.В., Жигалин Я.Л. Технология синтетических каучуков. Л.: Химия, 1987. C. 121.


