Разработка математической модели кирального метаматериала на основе цилиндрических спиральных элементов с учетом дисперсии и концентрации
Автор: Бучнев И.Ю., Клюев Д.С., Мамошина Ю.С., Осипов О.В., Панин Д.Н.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 2 т.26, 2023 года.
Бесплатный доступ
Обоснование. Интерес к исследованию метаматериалов СВЧ-диапазона связан с возможностью их использования для достижения заранее требуемых частотно и поляризационно селективных свойств взаимодействия с электромагнитным излучением, которые невозможно получить для структур на основе гомогенных сред. Цель. В работе рассмотрено построение математической модели кирального метаматериала на основе периодической матрицы произвольно ориентированных проводящих тонкопроволочных цилиндрических спиральных элементов, расположенных в однородной изотропной среде-контейнере. В отличие от известных моделей, она учитывает явный вид зависимости эффективной диэлектрической проницаемости и относительного параметра киральности от концентрации спиральных микровключений. Методы. При построении математической модели учитывается гетерогенность кирального метаматериала посредством формулы Максвелла Гарнетта, позволяющей определять эффективную диэлектрическую проницаемость по значениям проницаемостей среды-контейнера и области, занятой проводящими зеркально асимметричными включениями. В модели учтена дисперсия диэлектрической проницаемости с использованием квадратичной формулы Лоренца, а также дисперсия параметра киральности на основании модели Кондона. Результаты. Для исследуемого кирального метаматериала получены аналитические частотно-зависимые выражения для эффективной диэлектрической проницаемости и параметра киральности, учитывающие концентрацию спиральных включений и их геометрические параметры. Получена формула связи безразмерной объемной концентрации включений от расстояния между соседними элементами. Для расчета резонансной частоты проводящих тонкопроволочных цилиндрических спиральных элементов был применен квазистатический поход. Заключение. Предложенная методика построения математической модели может быть применена для киральных метаматериалов на основе периодических матриц проводящих элементов произвольной зеркально асимметричной пространственной конфигурации.
Киральная среда, киральный метаматериал, метаматериал, спираль, пространственная дисперсия, модель максвелла гарнетта, модель кондона, модель лоренца, концентрация элементов, параметр киральности, эффективная диэлектрическая проницаемость
Короткий адрес: https://sciup.org/140300674
IDR: 140300674 | УДК: 537.876.46 | DOI: 10.18469/1810-3189.2023.26.2.36-47
Текст научной статьи Разработка математической модели кирального метаматериала на основе цилиндрических спиральных элементов с учетом дисперсии и концентрации
В настоящее время существует громадное количество разнообразных материалов, таких как полимеры, композиты, керамика, сплавы, ферромагнетики и т. п. Многие материалы обладают естественными, присущими им свойствами взаимодействия с электромагнитным полем. Однако существует возможность изменить естественные свойства путем изменения пространственной структуры материалов. В большинстве случаев изменение электромагнитных свойств материалов связано с добавлением в них композитов различного рода. Одним из типов композиционных материалов являются так называемые метаматериалы [1–8]. Они активно исследуются различными учеными с начала XXI века. Наиболее сильный интерес к изучению метаматериалов возник после ряда публикаций [9–11] о возможности получения для них отрицательных значений показателя преломления, диэлектрической и магнитной прони- цаемостей, хотя о таких возможностях было известно давно [12]. Такие метаматериалы получили названия сред с отрицательным преломлением (LHM – Left Handed Media).
Любой метаматериал в СВЧ-диапазоне представляет собой совокупность некоторой среды, называемой контейнером, и некоторой совокупности композитов из материала с другими электрофизическими и геометрическими параметрами. Благодаря своим нестандартным свойствам взаимодействия с электромагнитным полем, метаматериалы находят широкое применение при разработке таких устройств, как антенны [13–17], поглотители [18–19], концентраторы СВЧ-энергии [20–21] и т. п.
Одним из важных типов метаматериалов являются искусственные киральные материалы (среды). Подобные среды исследуются уже давно – с 80-х гг. XX века [22–27]. Для создания кираль-ной среды используются проводящие композиты
LM^^e © Бучнев И.Ю. и др., 2023
с зеркально-асимметричной пространственной конфигурацией. В случае киральной (взаимной биизотропной) среды все зеркально-асимметричные композиты равномерно размещаются и хаотически ориентируются в однородной среде-контейнере. В случае одинаковой ориентации всех композитов среда называется бианизотропной. Киральные среды являются в некотором роде СВЧ-аналогами оптически активных сред и позволяют поворачивать плоскость поляризации электромагнитной волны на значительные углы в сантиметровом и миллиметровом диапазонах длин волн [28]. В качестве проводящих зеркальных композитов используется множество элементов с разной пространственной структурой, такие как элементы Теллегена [29], цилиндрические одно- и многозаходные тонкопроволочные спирали [30], S-элементы [31–33], гаммадионы [34] и т. п. Для описания свойств киральной среды вводится относительный параметр киральности χ . Основными свойствами электромагнитного излучения в киральной среде является распространение волн с право- (ПКП) и левокруговыми (ЛКП) поляризациями, а также кросс-поляризация падающей волны. Как следствие, возникают явления поворота плоскости поляризации и круговой дихроизм.
Вопросы о математической модели киральной среды возникают уже давно. В основе модели лежат материальные уравнения, которые записываются в различных формах [22–24]. В начале исследований электромагнитных свойств киральной среды ее материальные параметры считались постоянными, не зависящими от частоты. С одной стороны, в дальнейшем исследователи выбирали различные дисперсионные модели для диэлектрической проницаемости и параметра кираль-ности [35–36]. В основном для диэлектрической проницаемости использовалась модель Лоренца, а для параметра киральности, по аналогии с оптически активной средой, модель Кондона. Также в научной литературе известно использование дисперсионных моделей и для магнитной проницаемости [36].
С другой стороны, киральная среда является двухкомпонентной, то есть проявляет свойства гетерогенности. Впервые для описания свойства гетерогенности A.H. Sihvola использовал модель Максвелла Гарнетта [37], причем он применял эту модель для всех трех материальных параметров киральной среды. Также в [37] была предложена дисперсионная модель киральной среды на основе формулы Кондона. В [38] также для учета гете- рогенности была применена модель Максвелла Гарнетта.
В работах [39; 40] также предложены варианты математической модели киральной среды, учитывающие одновременно дисперсию материальных параметров и гетерогенность. В частности, было показано, что при малых концентрациях зеркально-асимметричных включений для учета гетерогенности среды можно использовать двухкомпонентные модели Максвелла Гарнетта [41; 42] или Бруггемана [41; 43].
Заметим, что в большинстве случаев дисперсионные и гетерогенные модели применяются в достаточной степени независимо друг от друга. В частности, необходима унификация зависимостей материальных параметров от концентрации зеркально-асимметричных включений различного типа. Во-первых, в диэлектрической проницаемости дисперсия должна учитываться не в среде-контейнере, а только в областях, в которых расположены проводящие включения. Во-вторых, необходимо использование безразмерной объемной концентрации микроэлементов (входящей в модели Максвелла Гарнетта и Бруггемана) как в соотношениях для диэлектрической проницаемости, так и для параметра киральности метаматериала.
Данная работа посвящена разработке математической модели кирального метаматериала на основе периодической матрицы произвольно ориентированных проводящих тонкопроволочных цилиндрических спиральных элементов, расположенных в однородной изотропной среде-контейнере. Предлагаемая модель кирального метаматериала одновременно учитывает зависимости эффективной диэлектрической проницаемости и параметра киральности от частоты и концентрации спиральных микровключений. При этом показана возможность некоторой унификации указанных зависимостей для различных типов зеркально-асимметричных включений.
1. Постановка задачи
Рассмотрим киральный метаматериал (КММ), представляющий собой равномерную матрицу из тонкопроволочных проводящих однозаходных спиральных элементов, расположенных в однородном диэлектрическом контейнере с относительной диэлектрической проницаемостью εc. Будем считать, что спиральные элементы намотаны вокруг цилиндров с относительной диэлектри- ческой проницаемостью sc и их высота равна высоте кирального метаматериала h. Метаматериал имеет геометрические размеры вдоль трех координатных осей lx, ly и h соответственно. Период матрицы из спиральных элементов определяется радиусом витка спирали (цилиндра) R и расстоянием между центрами цилиндров d; di = 2R + d. При постановке задачи считается, что периоды вдоль осей Ox и Oy равны между собой.
Безразмерная концентрация спиральных элементов определяется следующим образом:
NV
a =---1,
V
где N – общее количество спиральных элементов в метаматериале; V – объем метаматериала (объем параллелепипеда: V = l x l y h ); V - объем трехмерной фигуры, в которую вписан киральный элемент (для спиралей - объем цилиндра: V 1 = пR 2 h ).
Количество спиральных элементов определя- ется пространственным периодом матрицы элементов di = 2R + d и линейными размерами lx, ly контейнера кирального метаматериала.
Геометрия задачи приведена на рис. 1.
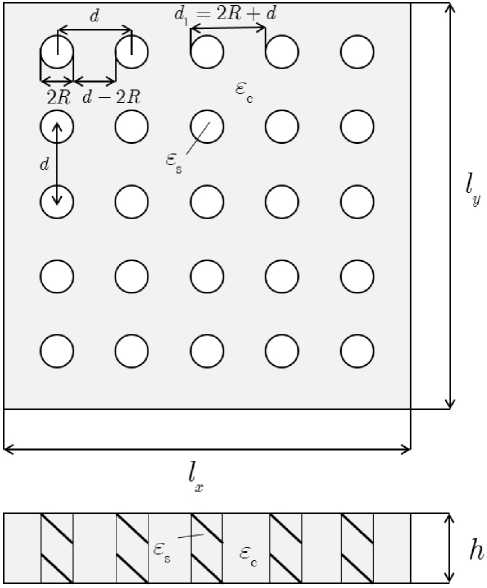
Рис. 1. Геометрия метаматериала
Fig. 1. Geometry of the metamaterial
2. Связь концентрации киральных элементов и расстояния между ними
SV V a =--------1-----=------1-----,
( 2 R + d ) 2 Sh ( 2 R + d ) 2 h
На первом этапе построения математической модели необходимо связать безразмерную кон-
где V 1 = п R 2 h .
Окончательно из соотношения (5) имеем:
центрацию спиральных элементов a с расстоянием между соседними элементами d .
Назовем элементарной ячейкой КММ область, содержащую одну спираль и промежуток до соседнего спирального элемента. Пространственный период элементарной ячейки d i = 2 R + d .
Количество элементарных ячеек вдоль оси Ox будет определяться следующим образом:
п R 2 a =----------.
( 2 R + d ) 2
Из формулы (6) получим квадратное уравнение относительно расстояния между спиральными элементами d :
d 2 + 4 Rd + 4 R 2 I 1
-—К 0 . 4a )
г = x = x x" d1 "2 R + d"
Решение уравнения (7) имеет вид
Количество элементарных ячеек вдоль оси Oy будет рассчитывается как
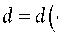
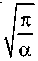
N = -y- = y y d1 2 R + d
.
Из соотношения (8) можно получить и обратное выражение:
Общее количество элементарных ячеек нахо-
дится как
N = NxNy
l l xy
( 2 R + d ) 2
S
( 2 R + d ) 2 ’
где S – площадь поверхности метаматериала. Из формулы (1) получаем:
п R 2 a =------- -.
( 2 R + d ) 2
Из соотношения (9) следует обобщение зависимости на случай произвольных киральных элементов:
a = S elem , d 1 2
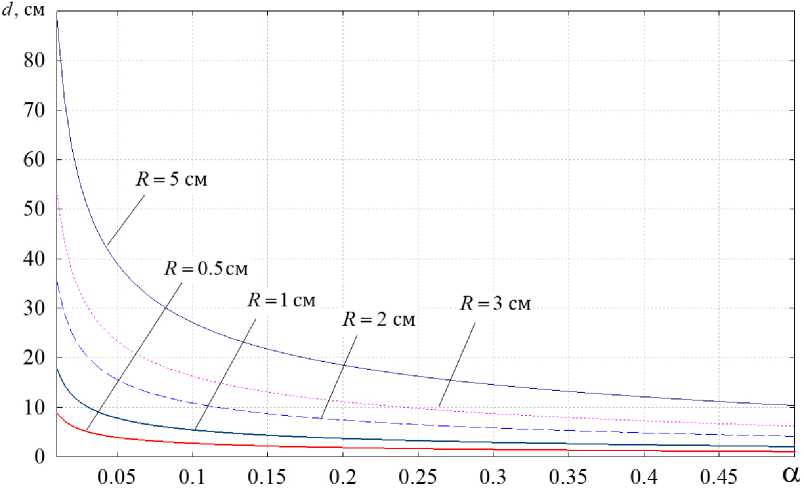
Рис. 2. Зависимость d = d ( а ) при различных значениях радиуса витка спирали Fig. 2. Dependence d = d ( а ) at different values of the radius of the spiral turn
то есть безразмерная концентрация киральных элементов в КММ равна отношению площади, занятой киральным элементом S e|em , к квадрату периода пространственной ячейки.
На рис. 2 представлена зависимость d = d ( а ) при различных значениях радиуса витка спирали.
3. Дисперсионная модель параметра киральности
Для описания частотной зависимости параметра киральности будем использовать обобщенную модель Кондона [1]:
, . OytoAto
х ( “ ) = 2 ' 2 . • (11
too —to — i ум где too - резонансная частота кирального элемента (определяется из квазистатической модели для конкретного типа элемента); у - частота демпфирования; Q^ — «сила» резонанса параметра киральности.
4. Расчет резонансной частоты спирального элемента
Зеркально-асимметричный элемент представляет собой тонкопроволочную проводящую одно-заходную спираль, состоящую из N витков радиуса R , расположенных друг от друга на расстоянии s (шаг спирали). Обозначим через l длину спирали в развернутом состоянии, а через r – радиус тонкой проволоки. На рис. 3 показано поперечное сечение спирального элемента. На рис. 3 введены
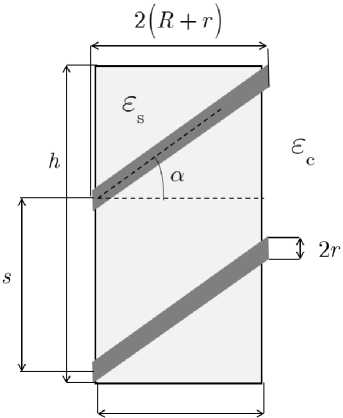
Рис. 3. Поперечное сечение спирального элемента
Fig. 3. Cross section of the spiral element следующие обозначения: h – высота контейнера; s – расстояние между витками спирали; R – внутренний радиус спирали; r – радиус проволоки; а - угол накрутки спирали; N - число витков спирали.
Для расчета резонансной частоты спирали использовалось квазистатическое приближение, расчет производился по формуле Томсона:
to0 = -/=. (12)
0 LC где L – индуктивность спирали; C – емкость спирали, учитывающая межвитковую и межэлемент- ную емкости, а также емкость самого проводника (проволоки).
Методика расчета резонансной частоты спирального элемента приведена в [15].
Резонансная частота спирали, показанной на рис. 3, вычисляется по следующей формуле:
K int =
/
to o =
c
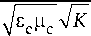
п Rr (R + r) N3
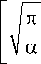
cos
п
2 (N +1)
5. Учет гетерогенности метаматериала
Гетерогенность учитываем по закону Максвелла
Гарнетта [2]:
к =
п N 2 R 2 +
18 Inf— 1-1
I r J п2N2R2 [(R + 2r)2 - R2 J (N2 -1)
+ hl + п R2 r (R + r) N3 ' dcos п—г
2 (N +1)
1 + 2as x s s -e c
-----------; Sx =----------, 1 -as s + 2s
где s - относительная эффективная диэлектрическая проницаемость метаматериала (как пространственной структуры, состоящей из контейнера и компонентов); sc - относительная диэлектрическая проницаемость контейнера; ss -относительная диэлектрическая проницаемость области, занятой компонентом; a - объемная без- размерная концентрация компонентов.
где c = у У^ о ^ о — скорость электромагнитной волны в вакууме.
Подставляя в формулу (13) выражение для расстояния между элементами через концентрацию (8), получаем выражение для резонансной частоты спирального элемента в следующем виде:
to o =
c
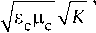
K = K self + K int i
6. Дисперсионная модель диэлектрической проницаемости
Для описания частотной зависимости диэлектрической проницаемости области, занятой ки-ральным элементом, будем использовать модель Лоренца [1]:
п N 2 R 2
K self =-----ТГГх--- +
18 In I 2 1 I-1
I r J
s s (to) =
^ s to 0
too -to - i yto
+
п 2 N 2 R 2 [ ( R + 2 r ) 2 - R 2 J ( N 2 -1 ) hl ;
K int =
п Rr (R + r) N3
|
l |
№-2] |
cos |
Г п ] |
|
2 ( N +1 ) |
|||
|
ra J |
где too - резонансная частота кирального элемента (определяется из квазистатической модели для конкретного типа элемента); у - частота демпфирования; Qs - «сила» резонанса диэлектрической проницаемости.
Подставляя выражение (17) в (16), получаем дисперсионную модель диэлектрической проницаемости КММ с учетом гетерогенности:
Используя соотношения (11) и (14), получаем
дисперсионную модель параметра киральности:
1 + 2asv s = sc-------x;
c 1 -as x
2 22
^stoo - sc I too -to - i Yto
s x
2 22
^stoo + 2sc I too -to - i Yto
. (18)
Qz to o to x(to) =
too -to - i Yto to0 =
c
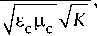
K = K self + K int ;
v _ п N 2 R 2
K self = +
18 In I 2 1 I-1
I r J п2N2R2 [(R + 2r)2 - R2 J (N2 -1)
+ hl 5
-
7. Материальные параметры кирального метаматериала на основе тонкопроволочных однозаходных спиральных элементов с учетом дисперсии и гетерогенности
Для описания КММ будем использовать следующий набор материальных параметров, определяемый из (15), (16) и (18):
1 + 2aE x ( ю ; a ) ё ( ю ; a ) = sc-------- 2 r;
v 7 1 -aE x ( ю ; a )
ю 0 ( a ) =
c
RR V K (a)
K ( a ) = K self + K 1nt ( a ) ;
Qztoo(a)ю х ю; a I =------
V 2 / \2 •
Ю о ( a ) -ю - 1 ую
О е ю о ( a ) -E c R Н-ю 2 - 1 R
Ex(ю; a)=——r^—2
□ЕЮо (a) + 2ec I Юо (a)-ю -1ую I юо (a)= /—; K(a)=Kself+Kint (a); VEc^c VK(a)
K self =
n N 2 R 2
-^—+ , I 2 1
18 in - -1 r
n 2 N 2 r 2 ^ ( r + 2 r ) 2 - R 2 J ( N 2 -1 hl
K 1nt ( a ) =
n Rr ( R + r ) N 3
„ n N 2 R 2
K self =
18 in I - I-1
I r J
l
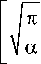
-2
cos
П
2 ( N +1 )
n 2 N 2 R 2 ^ ( R + 2 r ) 2 - R 2 J ( N 2 - 1 hl
Математическая модель, определяемая соотношениями (21) и (22), описывает киральный метаматериал, созданный на основе равномерно размещенных тонкопроволочных проводящих однозаходных спиральных элементов (рис. 1).
K int ( a ) =
n Rr ( R + r ) N 3
П П l J--2 cos —,-----7
V a J 2 ( N +1 )
-
8. Материальные уравнения для кирального метаматериала на основе тонкопроволочных однозаходных спиральных элементов с учетом дисперсии и гетерогенности
-
9. Дисперсионные уравнения для нормальных волн кирального метаматериала на основе тонкопроволочных однозаходных спиральных элементов с учетом дисперсии и гетерогенности
Материальные уравнения для киральной среды имеют вид [3]:
Расчет дисперсионных характеристик (постоянных распространения) нормальных волн кираль-ного метаматериала с право- и левокруговыми поляризациями осуществляется по следующим формулам:
—* —* —* —* —* —*
D =e E + 1 x H ; B = ц H ± 1 x E ,
kRL ( ю ; a ) = -^ I ^е(ю ; a ) ц ±х ( ю ; a ) I , (23)
где e - относительная эффективная диэлектриче ская проницаемость; ц - относительная магнитная проницаемость; х — относительный параметр киральности метаматериала.
Материальные уравнения (20) являются частотно- зависимыми, а также материальные параметры КММ в них зависят от объемной безразмерной концентрации киральных микроэлементов a:
|
I— = ё ( ю ; a ) E —+ 1 х ( ю ; a ) H ; B = ц H ± 1 х ( ю ; a ) E — , |
(21) |
|
где |
|
|
1 + 2aE x ( ю ; a ) ё ( ю ; a ) = E c / . ; v ' c 1 -aE x ( ю ; a ) |
(22) |
П х ю о ( a ) ю
-
X ю ; a =----------------- ;
V ' 2 / \ 2 • юо (a)-ю -1 ую
О е ю о ( a ) -E c R Н-ю 2 - 1 R е х ( ю ; a ) =-----------------------------------
Ц.ю2 (a) + 2e, I ю0 (a)-ю2 -1 ую где
-
1 + 2aEx (ю; a) e (ю; a) = ec----------2-;
-
v ' c 1 -aE x ( ю ; a )
П х ю о ( a ) ю
-
X ю; a =------
- V ' 2 / \2 •
ю о ( a ) -ю - 1 ую
П е ю 0 ( a ) -E c R ( a ) -ю 2 - 1 V ю ]
ex (ю; a) =-----------------j=i
-
□Ею 0 ( a ) + 2e , I ю 0 ( a ) -ю 2 - 1 ую
ю 0 ( a ) =
c
Тё С ^ С V K ( a )
K ( a ) = K self + K 1nt ( a ) ;
n N 2 R R2
K self = TTa +
18 ln I 2l I-1
I r J
П 2 N 2 r 2 [ ( r + 2 r ) 2 - R 2 J ( N 2 -1 )
+ hl 5
K int ( a ) =
n Rr ( R + r ) N 3
го 0 ( a ) =
|
l |
[^-21 |
cos |
[ п .1 |
|
2 ( N +1 ) |
|||
|
_^а _ |
10. Обобщение модели КММ при одновременном учете дисперсии и гетерогенности
Представим емкостной коэффициент K ( а ) = = K self + K int (а) в виде
K ( а ) = K self + K int ( a ) ; (24)
K self
, n N 2 R 2
= k =----7—x--+
18 In I 2l I-1 r
n 2 N 2 R 2 [ ( R + 2 r ) 2 - R 2 ] ( N 2 - 1 )
+ hl ;
K int ( a ) =
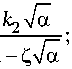
n Rr ( R + r ) N 3
I " Л
2 l. —cos —,----
V 4a [ 2 ( N +1 )
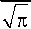
Формулу для резонансной частоты в зависимости от безразмерной объемной концентрации можно обобщить следующим образом:
® 0 ( a ) =
v
k ^ +
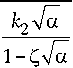
Аналогично с использованием формулы (26) можно получить обобщенную зависимость эффективной диэлектрической проницаемости от безразмерной объемной концентрации:
б ( го ; а ) = б с
Б х ( го ; а ) =
го 0 ( а ) =
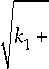
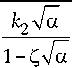
где v = c /( ^е с Ц с ) — фазовая скорость электромагнитной волны в среде-контейнере; коэффициенты k j ( j = 1 , 2 ) имеют размерность квадрата длины и определяются геометрическими размерами ки-ральных элементов и их типом; Z — безразмерная
константа.
С использованием формулы (25) можно получить обобщенную зависимость относительного параметра киральности от безразмерной объем-
ной концентрации:
Q z ® 0 ( а ) ю
X го ; а =---------------------;
v ' 2 / х 2- roolaj-ro - i уго
1 + 2аБ х ( го ; а )
1 -аБ х ( го ; а )
□ е го 0 ( а ) -Б с ^го 2 ( а ) -го 2 - i уго^
□ е го 0 ( а ) + 2б с I го 0 ( а ) -го 2 - i уго
v
k ^ +
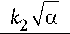
1 -;7а
Формулы (26) и (27) описывают обобщенные зависимости материальных параметров кирального метаматериала от частоты го и безразмерной объемной концентрации киральных элементов а .
Заключение
В работе рассмотрены принципы построения математической модели кирального метаматериала на основе периодической матрицы произвольно ориентированных проводящих тонкопроволочных цилиндрических спиральных элементов, расположенных в однородной изотропной среде-контейнере.
Построенная математическая модель кирально-го метаматериала на основе периодической матрицы произвольно ориентированных проводящих тонкопроволочных цилиндрических спиральных элементов учитывает гетерогенность кирального метаматериала, дисперсию диэлектрической проницаемости, дисперсию параметра киральности, а также зависимость материальных параметров от концентрации спиральных включений.
Предложенная методика построения математической модели может быть применена для киральных метаматериалов на основе периодических матриц проводящих элементов произвольной зеркально-асимметричной пространственной конфигурации.
Список литературы Разработка математической модели кирального метаматериала на основе цилиндрических спиральных элементов с учетом дисперсии и концентрации
- Capolino F. Theory and Phenomena of Metamaterials. Boca Raton: Taylor & Francis – CRC Press, 2009. 992 p.
- Engheta N., Ziolkowski R.W. Metamaterials: Physics and Engineering Explorations. Hoboken: Wiley, 2006. 414 p.
- Iyer A.K., Alù A., Epstein A. Metamaterials and Metasurfaces – Historical Context, Recent Advances, and Future Directions // IEEE Transactions on Antennas and Propagation, 2020. Vol. 68, no. 3. P. 1223‒1231. DOI: https://doi.org/10.1109/TAP.2020.2969732
- A review on metamaterials for device applications / S.N. Kumar [et al.] // Crystals. 2021. Vol. 11, no. 5. P. 518. DOI: https://doi.org/10.3390/cryst11050518
- Zheludev N.I. A Roadmap for metamaterials // Opt. Photonics News. 2011. Vol. 22, no. 3. P. 30–35. DOI: https://doi.org/10.1364/OPN.22.3.000030
- Metamaterial analog of electromagnetically induced transparency / N. Papasimakis [et al.] // Phys. Rev. Lett. 2008. Vol. 101. P. 253903.
- Zheludev N.I. The road ahead for metamaterials // Science. 2010. Vol. 328, no. 5978. P. 582–583. DOI: https://doi.org/10.1126/science.1186756
- Вендик И.Б., Вендик О.Г. Метаматериалы и их применение в технике сверхвысоких частот (Обзор) // Журнал технической физики. 2013. Т. 83, № 1. C. 3‒28. URL: https://journals.ioffe.ru/articles/viewPDF/41403
- Composite medium with simultaneously negative permeability and permittivity / D.R. Smith [et al.] // Phys. Rev. Lett. 2000. Vol. 84, no. 18. P. 4184–4187. DOI: https://doi.org/10.1103/PhysRevLett.84.4184
- Shelby R.A., Smith D.R., Schultz S. Experimental verification of a negative index of refraction // Science. 2001. Vol. 292, no. 5514. P. 77–79. DOI: https://doi.org/10.1126/science.1058847
- Pendry J. A chiral route to negative refraction // Science. 2004. Vol. 306, no. 5700. P. 1353–1355. DOI: https://doi.org/10.1126/science.1104467
- Veselago V.G. The Electrodynamics of substances with simultaneously negative values of ε and μ // Soviet Physics Uspekhi. 1968. Vol. 10, no. 4. P. 509–512. DOI: https://doi.org/10.1070/PU1968v010n04ABEH003699
- Слюсар В.И. Метаматериалы в антенной технике: история и основные принципы // Электроника: НТБ. 2009. № 7. С. 10‒19. URL: https://www.electronics.ru/files/article_pdf/0/article_287_909.pdf
- Pozar D.M. Microstrip antennas and arrays on chiral substrates // IEEE Transactions on Antennas and Propagation. 1992. Vol. 40, no. 10. P. 1260‒1263. DOI: https://doi.org/10.1109/8.182462
- Импедансные характеристики двухэлементной антенной решетки с киральной подложкой / А.Л. Бузов [и др.] // Письма в ЖТФ. 2018. Т. 44, № 23. С. 37‒45. URL: https://journals.ssau.ru/pwp/article/view/7078
- Перспективы использования метаматериалов в антеннах нового поколения / А.Л. Бузов [и др.] // Физика волновых процессов и радиотехнические системы. 2017. Т. 20, № 3. С. 15‒20. URL: https://journals.ssau.ru/pwp/article/view/7078
- Investigation of circularly polarized patch antenna with chiral metamaterial / Y. Liu [et al.] // IEEE Antennas and Wireless Propagation Letters. 2013. Vol. 12. P. 1359–1362. DOI: https://doi.org/10.1109/LAWP.2013.2286191
- Metamaterial electromagnetic cloak at microwave frequencies / D. Schurig [et al.] // Science. 2006. Vol. 314, no. 5801. P. 977–980. DOI: https://doi.org/10.1126/science.1133628
- Tunable electromagnetically induced transparency from a superconducting terahertz metamaterial / C. Zhang [et al.] // Appl. Phys. Lett. 2017. Vol. 110, no. 24. P. 241105. DOI: https://doi.org/10.1063/1.4985618
- Wide band fractal-based perfect energy absorber and power harvester / M. Bağmancı [et al.] // International Journal of RF and Microwave Computer-Aided Engineering. 2019. Vol. 29, no. 7. P. e21597. DOI: https://doi.org/10.1002/mmce.21597
- Осипов О.В., Юрасов В.И., Почепцов А.О. Киральный метаматериал для частотно-селективной концентрации энергии сверхвысокочастотного излучения // Инфокоммуникационные технологии. 2014. Т. 12, № 4. С. 76‒82.
- Electromagnetic Waves in Chiral and Bi-Isotropic Media / I.V. Lindell [et al.]. London: Artech House, 1994. 291 p.
- Lakhtakia A., Varadan V.K., Varadan V.V. Time-Harmonic Electromagnetic Fields in Chiral Media. Lecture Notes in Physics. Berlin: Springer-Verlag, 1989. 121 p.
- Caloz C., Sihvola A. Electromagnetic chirality, Part 1: The microscopic perspective [electromagnetic perspectives] // IEEE Antennas and Propagation Magazine. 2020. Vol. 62, no. 1. P. 58‒71. DOI: https://doi.org/10.1109/MAP.2019.2955698
- Третьяков С.А. Электродинамика сложных сред: киральные, би-изотропные и некоторые бианизотропные материалы // Радиотехника и электроника. 1994. Т. 39, № 10. С. 1457‒1470.
- Киральные электродинамические объекты / Б.З. Каценеленбаум [и др.] // Успехи физических наук. 1997. Т. 167, № 11. С. 1201‒1212. DOI: https://doi.org/10.3367/UFNr.0167.199711c.1201
- Sochava A.A., Simovski C.R., Tretyakov S.A. Chiral effects and eigenwaves in bi-anisotropic omega structures // Advances in Complex Electromagnetic Materials. Dordrecht: Springer, 1997. P. 85–102.
- Resonant features of planar Faraday metamaterial with high structural symmetry / S.Y. Polevoy [et al.] // Eur. Phys. J. Appl. Phys. 2013. Vol. 61, no. 3. P. 030501. DOI: https://doi.org/10.1051/epjap/2013120320
- Tretyakov S.A., Mariotte F. Maxwell Garnett modeling of uniaxial chiral composites with bianisotropic inclusions // Journal of electromagnetic waves and applications. 1995. Vol. 9, no. 7-8. P. 1011–1025. DOI: https://doi.org/10.1163/156939395X00695
- Осипов О.В., Плотников А.М., Салимова Н.Р. Использование эффекта азимутального рассеяния электромагнитных волн метаструктурой на основе элементов Телледжена в прикладных задачах электродинамики // Инфокоммуникационные технологии. 2012. Т. 10, № 1. С. 8‒15.
- Просвирнин С.Л. Преобразование поляризации при отражении волн микрополосковой решеткой из элементов сложной формы // Радиотехника и электроника. 1999. Т. 44, № 6. С. 681–686.
- Васильева Т.Ц., Просвирнин С.Л. Дифракция электромагнитных волн на плоской решетке из киральных полосковых элементов сложной формы // Физика волновых процессов и радиотехнические системы. 1998. Т. 1, № 4. С. 5–9.
- Prosvirnin S.L. Analysis of electromagnetic wave scattering by plane periodical array of chiral strip elements // Proceedings of 7th International Conference on Complex Media «Bianisotropic ’98». 1998. P. 185–188.
- Zhao R.L., Zhang J., Soukoulis C.M. Conjugated gammadion chiral metamaterial with uniaxial optical activity and negative refractive index // Phys. Rev. B. 2011. Vol. 83, no. 3. P. 035105. DOI: https://doi.org/10.1103/PhysRevB.83.035105
- Semchenko I.V., Tretyakov S.A., Serdyukov A.N. Research on chiral and bianisotropic media in Byelorussia and Russia in the last ten years // Progress in Electromagnetics Research. 1996. Vol. 12. P. 335‒370.
- Prudêncio F.R., Silveirinha M.G. Optical isolation of circularly polarized light with a spontaneous magnetoelectric effect // Phys. Rev. A. 2016. Vol. 93, no. 4. P. 043846. DOI: https://doi.org/10.1103/PhysRevA.93.043846
- Sihvola A.H. Temporal dispersion in chiral composite materials: A theoretical study // Journal of electromagnetic waves and applications. 1992. Vol. 6, no. 7. P. 1177–1196. DOI: https://doi.org/10.1163/156939392X01705
- Lakhtakia A., Varadan V.K., Varadan V.V. On the Maxwell Garnett model of chiral composites // Journal of Materials Research. 1992. Vol. 8, no. 4. P. 917–922. DOI: https://doi.org/10.1557/JMR.1993.0917
- Аралкин М.В., Дементьев А.Н., Осипов О.В. Математические модели киральных метаматериалов на основе многозаходных проводящих элементов // Физика волновых процессов и радиотехнические системы. 2020. Т. 23, № 1. С. 8‒19. DOI: https://doi.org/10.18469/1810-3189.2020.23.1.8-19
- Аралкин М.В., Дементьев А.Н., Осипов О.В. Исследование электромагнитных характеристик планарных киральных метаструктур на основе составных спиральных компонентов с учетом гетерогенной модели Бруггемана // Физика волновых процессов и радиотехнические системы. 2020. Т. 23, № 3. С. 44‒55. DOI: https://doi.org/10.18469/1810-3189.2020.23.3.44-55
- Сушко М.Я., Криськив С.К. Метод компактных групп в теории диэлектрической проницаемости гетерогенных систем // Журнал технической физики. 2009. Т. 79, № 3. С. 97‒101. URL: https://journals.ioffe.ru/articles/9645
- Garnett J.C. Maxwell. Colours in metal glasses and in metallic films // Phylos. Trans. R. Soc. London. Ser. A. 1904. Vol. 203. P. 385‒420.
- Bruggeman D.A.G. Berechnung verschiedener physikalischer Konstanten von eterogenen Substanzen, I. Dielektrizitatskonstanten und Leitfahigkeiten der Mischkorper aus isotropen Substanzen // Ann. Phys. 1935. Vol. 416, no. 7. P. 636‒664. DOI: https://doi.org/10.1002/andp.19354160705


