Разработка математической модели массопереноса компонент водно-солевого раствора в пучинистых грунтах на основании кинетической теории жидкостей

Сезонные процессы морозного пучения оказывают существенное влияние на устойчивость зданий и сооружений, поэтому их прогнозирование является актуальной задачей.

Известно, что морозное пучение грунтов развивается в результате перемещения влаги из теплых зон грунта в холодные. Пересекая фронт промерзания, грунтовая влага замерзает и образует скопления ледяных шлиров. Особенно интенсивно пучения развиваются под сооружениями, которые способны поддерживать в грунте температуры около –6…–0,5 °С (например под газо- и конденсатопроводами [1, 2]), что связано с высокой проницаемостью грунтов при данных температурах [3].

Прогнозирование процессов перемещения поровой влаги, величины вертикальной деформации и давления морозного пучения на сегодняшний день осложняется отсутствием единой физической модели фильтрационно-диффузионных процессов в талых, промерзающих и мерзлых грунтах. Несмотря на значительное количество гипотез о природе сил, вызывающих перемещение влаги, многие из них не имеют достаточной количественной основы, позволяющей проводить расчеты [4]. В связи с этим активно развивалось феноменологическое направление, посвященное установлению количественных соотношений между эмпирическими закономерностями.

Наиболее часто в мировой гидрофизике грунтов для моделирования динамики поровой влаги применяются различные модификации уравнения Ричардса [5, 6]. И.Л. Калюжный и С.А. Лавров рекомендуют следующие уравнения для описания движения почвенной влаги [4]:

g гр =-Р вС ~(^ W +^ w V П + g V H 'l - РЛ ё -;          (1)

g I ^d W H3        ^д П           )

Механика

4 = -V ■ ( M s gZ ) - V ■ ( PCD. V ...) ;                       (2)

"4 = - ^v ( m , g BC ) ,                             ⁽³⁾

-2р где gвс - вектор суммарного массового потока водно-солевого раствора через единицу поверхности грунта, кг/(м2-с); р“с - истинная плотность водно-солевого раствора, кг/м3; X, - коэффициент влагопроводности, совпадающий с коэффициентом фильтрации, м/с; у, - капиллярносорбционный потенциал воды, Дж/кг; WH3 - влажность по незамерзшей воде как отношение массы незамерзшей воды к массе твердых нерастворимых компонентов грунта, д. ед.; П - пористость (отношение объема пор к объему твердых нерастворимых компонентов грунта), д. ед.; р, - водосодержание как отношение массы незамерзшей воды к объему грунта, кг/м3; psр - солесо-держание как отношение массы растворенных солей к объему грунта, кг/м3; м, , Ms - массовая доля воды и солей в незамерзшем водно-солевом растворе, д. ед.; D,s - эффективный коэффициент диффузии солей в грунте, м2/с; рв. - растворосодержание, как отношение массы незамерзшего раствора к объему грунта, кг/м3; H - гидравлический напор, м; ez - единичный вектор вдоль оси z (вертикальная ось).

При отрицательных температурах формула (1) по-прежнему применима для описания потока влаги в грунте, однако частичное замерзание поровой влаги приводит к тому, что теперь капиллярно-сорбционный потенциал у , является лишь только функцией температуры T , поэтому при отрицательных температурах ее можно записать в следующей форме

Тр = - р вс^ (V T + g V H 1 - р-e z ,                  (4)

g V d T           )

где T- температура, К.

Уравнения (1)-(4) позволяют рассчитать плотность потока воды и солей в талых, промерзающих и мерзлых грунтах. Интегрирование уравнения (3) позволяет рассчитать массу сегрегационного льдовыделения.

Приведенные уравнения позволяют удовлетворительно описывать процессы массообмена с необходимой для инженеров точностью, однако, как будет показано ниже, они не позволяют провести четкого разделения и оценки вклада каждого механизма массопереноса в суммарный процесс переноса масс и учесть подвижность адсорбированных молекул.

Авторы статьи поставили задачу рассмотреть модель, в которой явления диффузионного массопереноса воды и солей как в талых, так и промерзающих, и мерзлых грунтах происходят при наличии градиентов содержания воды р , и соли р ^ в грунте, температуры T , пористости П, давления P с учетом неодинаковой подвижности компонентов вблизи минеральной поверхности и в объемном растворе.

Известно, что в однородном по физико-механическим свойствам грунте при постоянном внешнем давлении, температуре и концентрации раствора вода перемещается из зоны с высокой влажностью в зону с низкой влажностью. Этот массоперенос обусловлен двумя основными механизмами: фильтрация и диффузия. Явление диффузии, в данной ситуации её обычно называют плёночной диффузией, происходит в плёнках водно-солевого раствора, адсорбированных на поверхности минеральных частиц грунтовой системы.

С позиций кинетической теории жидкостей, разработанной Френкелем, переход молекулы из одного положения равновесия в другое можно рассматривать как последовательность двух событий: «испарение» из первоначального положения равновесия в промежуточное с последующей «конденсацией» в новое положение равновесия. В этом случае среднюю скорость перемещения молекулы можно рассматривать как дистанцию между двумя положениями равновесия (равную длине свободного пробега в жидкости), деленную на время пребывания молекулы равновесии [7]:

Марков Е.В., Пульников С.А., Гербер А.Д.

u =

£ т

= — exp ^т о

EN

kT

= —exp ^т о

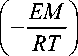
где u – средняя скорость перемещения молекулы в произвольном направлении, м/с; δ – длина свободного пробега молекулы жидкости между двумя положениями временного равновесия, м; т - среднее время пребывания молекулы около временного положения равновесия, с; т₀ - среднее время пребывания молекулы около временного положения равновесия при отсутствии дополнительного потенциального барьера, с; E_N – потенциальный барьер на одну частицу, Дж; E – потенциальный барьер на 1 кг вещества, Дж/кг; k – постоянная Больцмана, Дж/К; T – температура, К; M – молярная масса, кг/моль; R = 8,31 – универсальная газовая постоянная, Дж/(моль∙К). С учетом принципиального отличия жидкости от газа будем считать, что длина пробега δ не подчиняется закону Клаузиуса, а имеет приблизительно одну и ту же величину [7].

Получим уравнение для диффузионного потока в грунте, основываясь на теории Френкеля для i-й компоненты водно-солевого раствора. Проведем в объеме грунта три плоскости: x = x0, x = x0 + 5i, x = x0 - 5i. Если длина свободного пробега молекулы i-й компоненты равна di, тогда плоскость x = x0 могут пересечь лишь те молекулы, что находятся в пределах x = x0 ± 5i. Так как молекулы могут двигаться в 6 различных направлениях (вперёд-назад, вверх-вниз, влево-вправо), то масса жидкости, пересекающая плоскость x = x0 снизу вверх, равна

^A m ee = 1 1 р"\   s_n^A | A x А У ^A z ,

6 <    ^lx 0 ^-di /2 )

где

^P i l x о - £ /2

- парциальная плотность i -й компоненты водно-солевого раствора, кг/м³; 9 -

объемная доля воды в грунте, д. ед. Тогда плотность массового потока, проходящего через плос- кость x = x0 снизу вверх в единицу времени, равна ри1

_ = Amee =   । x0-5i/2 Ax gee AyAz At        6

Но Ax = di, At = Ti, поэтому с учетом (5) имеем gBB = 6(^р" )|x0-£/2, где рГ - содержание i-го компонента в единице объема грунта, кг/м3.

Аналогичную формулу имеем и для потока, идущего сверху вниз, двн = 1 (РРгр)| . о/?.

6 ^{х      7}l x 0+ £ /2

Если принять, что плотность массового потока мало меняется с расстоянием, то можем разложить её в ряд Тейлора и оставить только первые слагаемые:

Тогда, оси x ,

( ирР )1-2>/2 1/           id ( u,Р гр)   § g =-------- b x o_ 5 i /2 = 1 , р      - 1 ( ini ) d, ;                    (10) 5    вв           6           6 ( 1P1 ) x 0 6 d x        2                           ’ x 0 ( U iP 'P )L+J/2                 id ( u,р/Р)    8 g    =------ ^0± 5 i /£ = 1 u; р гР + 1            5 .                (ii) 5    вн           6           6 ( 1P1 ) x 0 6     d x        2                           ’ x 0 для результирующей плотности массового потока i -го компонента, в направлении 5 . d ( u P ) gi , x = g ee двн =         з .                                   (12) 6     o x

Механика

Обобщая уравнение (12), запишем его в векторной форме с учетом (5):

g i =

st

⁶ ( ^T 0 )

V f Pr exp к

E i M i В RT )) ,

где g_i – чисто диффузионная плотность массового потока i -го компонента, как отношение массового расхода к площади поверхности грунта, кг/(с∙м²).

На следующем этапе рассмотрим водно-солевой раствор в грунте в виде двух компонентов: растворенных солей и воды и присвоим соответствующую нижнюю индексацию s и w . Тогда имеем два чисто диффузионных потока:

gw

-SW - f n .-(EwMw/RT) Y V I pwe                  I ;

6 (t0 ) w к                   7

gs

—^S2 ^- f _OPPe - ( Es M s / RT )

^V I ^p s e

^{6 ( t} o ) _s к

.

Поскольку известно [8], что вода в грунте вблизи поверхности минеральных частиц находится в связанном состоянии, то её энергетический барьер отличается от такового для свободной воды на какую-то дополнительную величину. С позиций термодинамики энергетический барьер это дополнительная энергия, которую необходимо затратить для удаления вещества из указанного места в адсорбированной плёнке. Известно, что капиллярно-сорбционный потенциал воды Vw (Pw ,®w, П) — это энергия, которую необходимо затратить, чтобы добавить единицу массы воды в адсорбированную плёнку, и является функцией водосодержания pw, концентрации tow и пористости грунта П. Понижение химического потенциала растворителя по сравнению с чистым веществом pw (tow) - это энергия, которую необходимо затратить, чтобы добавить единицу мас- сы воды в раствор, и она является ния, получаем:

функцией концентрации. Таким образом, исходя из определе-

gw

- s W

6(t0 )w

f

*

V P w e

к

- ( E W M w / RT ) eM w ( V w + P W ) / RT '

;

gs

S

6 (T0 ) s

*

V РГ e к

- ( E S M s / RT ) M s ( V s + P ^ ) / RT

.

Следует заметить, что капиллярно-сорбционный потенциал p _w изменяется по толщине плёнки довольно значительно (от –0,1 Дж/кг в состоянии полного водонасыщения грунта до ≈ –2 МДж/кг при нулевой влажности [9]), а, следовательно, поток g_w изменяется еще сильнее, так как p _w является показателем экспоненты. Это подтверждается многочисленными экспериментами, в ходе которых была установлена низкая подвижность молекул воды вблизи минеральной поверхности [8]. Следовательно, в пределах рассматриваемого поперечного сечения грунта молекулы более близко расположенные к минеральной поверхности будут диффундировать значительно медленнее, чем молекулы в свободном поровом пространстве. Чтобы учесть различие в скоростях диффузии и сохранить формализм уравнений фильтрационного типа, необходимо усреднить чисто диффузионную плотность массового потока по сечению грунта:

gw

^SW v 6 (Т0 )W

P w

-1- f Р гр е гр w

- ( E w M w / RT ) M w ( p w ⁺ P w ) / RT e

\

к

гр pw

gs

S

6 (T0 ) s

V

к

P ?

— f Р г ^р е гр s ^p s  0

- ( E 0 M s / RT ) M s ( V s + P s ) / RT e

d p P ;

) d p р .

Марков Е.В., Пульников С.А., Гербер А.Д.

Для случая диффузии в свободном растворе при постоянной температуре можем получить следующие закономерности:

^7 = — 5 ^-e ^{1 gw} 6 ( T o ) w

V( pw )= Dw V( pw);

, . = 6 T . l E s MRT^ D^ )

Интересно сравнить классические выражения для диффузионных потоков с аналогичными из кинетической теории жидкости. Величину чисто диффузионных потоков можно записать через сумму диффузионных потоков и конвективного потока, помноженного на концентрацию соответствующего компонента:

g w ^ w ( g w ⁺ g s ) ⁺ j w , g s = ® s ( g w ⁺ g s ) ⁺ j s •

Тогда, исходя из (22) и (23), диффузионные потоки записываются следующим образом: j w = ^- j s = ® s g w ^- ® w g s

Для простейшего случая диффузии в объемном растворе из (20)–(21) получаем:

1W =- 1s ="®sDw V ( pw ) + ®wDs V ( PsИ ) .

В тоже время классическое выражение для диффузионного потока записывается следующим образом:

w

^e j s = - D„ p« ^VV w ) =-rn , D ws ^V ( p W ) ⁺ M w D ws v ( p s ) .

Сравнивая (25) и (26) приходим к выводу, что в соответствии с кинетической теорией жидкости классическое уравнение диффузии (26) справедливо только в частном случае D w = D_s .

Из уравнений (19)–(20) становится видно, что чисто диффузионные потоки соли и воды, вообще говоря, могут быть различными. В тоже время сумма диффузионных потоков обычно принимается равной нулю [10] как в уравнении (26). Последнее допущение обуславливает неучтенную конвекцию диффузионного типа, которая представляет собой перекрестный эффект диффузии и для объемного раствора описывается следующей формулой g ws = gw + gs = Dw V( pW ) Ds V( p" ) ,

где g _ws – перекрестный эффект диффузии, выражающий конвективный поток всего раствора, кг/(с∙м²).

Для расчета коэффициентов D_w и D_s требуется не менее 4-х измерений скорости диффузии при различных температурах. Температурная зависимость коэффициентов диффузии позволяет также рассчитать термодиффузию компонентов, которая на 1–2 порядка меньше концентрационной.

Окончательные выражения для диффузионного массопереноса компонент водно-солевого раствора в грунте с учетом выражений (20)–(21) для коэффициентов диффузии в объемном растворе записываются следующим образом:

g dw

._v D     '

V

гр pw

^p w г _D ^M - ( V w + P W ) / R ^T J P Pe '          ’ i

\

d p P ;

g ds

._v D s T

Р Г V

^p гЛ(Vs + P' s ) / RT

J P гр e

^ dp.

Выпишем выражение для фильтрационного потока воды и соли с учетом градиента давления, исходя из выражения (4):

Механика

g = -Km ^f р и ^ w^- Р + Р и   у п + у P

fw P w w w w l  дргр          дП        )

g_f -A_Pto_s ^f Р и —P + р и ?^У П + У P

• ^gfs P s ^p w -_ .ppp ^p w ^p w

l   Ppw                       у где λP – коэффициент влагопроводности по Колунину [11].

Для случая температуры ниже начала замерзания водно-солевого раствора необходимо положить ∇ П = 0 , так как в этом случае растворосодержание ρ_w ^гр , а, следовательно, и потенциал ψ_w определяются только температурой [4].

Таким образом, теперь можно записать уравнения массопереноса, в которых структурно выделены в явном виде слагаемые, связанные с массопереносом вещества за счет различных механизмов:

∂ ρ w ^гр

∂t

^-V " ( g dw

+ g _fw ) ,

∂ρsгр ∂t где диффузии соответствуют потоки g dw

= -∇ ⋅ ( g ds + g fs ) , и g ds , а фильтрации соответствуют потоки

^g fw и

g fs .

Выражения (28)–(29) показывают, что диффузионный поток соли и воды является функцией следующих величин: ρ_w ^гр , ρ_s ^гр , T . Таким образом, использование кинетической теории жидкости взамен феноменологических законов позволило составить математическую модель диффузии, которая позволяет описать одновременно термодиффузию и концентрационную диффузию Фика в грунтах и учесть неодинаковую подвижность молекул в адсорбированной плёнке. Выражения (30)–(31) для фильтрационного потока позволяют дополнительно учитывать конвективный мас-соперенос как функцию ρ_w ^гр , П, P .

Выводы

Используя подход, основанный на кинетической теории жидкости, построена математическая модель массопереноса в грунтовой среде, позволяющая в явном виде определить вклад различных механизмов.

На основе данного подхода получены выражения для плотности чисто диффузионного потока воды и растворенных солей с учетом неодинаковой подвижности молекул в адсорбированной плёнке (28)–(29) и позволяющие описать одновременно термодиффузию и концентрационную диффузию Фика.

Показано, что классическое выражение для плотности диффузионного потока справедливо только в частном случае равенства коэффициентов диффузии каждого компонента в соответствии с кинетической теорией жидкости (26)–(27).