Разработка математической модели процесса сушки плодов черной смородины в вакуум-аппарате с СВЧ - энергоподводом

Журавлев А.В., Виниченко С.А, 2014

Процесс сушки плодов черной смородины является чрезвычайно сложным, поэтому к математической модели процесса предъявляются высокие требования. В процессе сушки плоды уменьшаются в объеме ориентировочно в 3-4 раза, существенно изменяются физические характеристики (некоторые - на несколько порядков) как отдельного плода, так и слоя плодов в сушильной установке.

Многие известные модели процесса сушки используют приближения постоянства геометрических параметров объекта сушки и постоянства его физических свойств [1-5]. Однако при описании СВЧ-сушки плодов черной смородины такие модели имели бы низкую адекватность. Поэтому в настоящей работе поставлена задача разработать математическую модель процесса сушки, обладающую высокой детализацией и высокой адекватностью, базирующейся на общепринятых уравнениях сушки, но использующей в полной мере вычислительные возможности современных компьютеров [6].

Разрабатываемая модель должна описывать целый ряд физических процессов, протекающих при сушке слоя плодов черной смородины:

• -    изменение формы отдельного плода;

• -    изменение структуры слоя плодов;

• -    внутренний тепло- и влагообмен внутри плода;

• -    тепло- и влагообмен в слое плодов;

• -    тепло- и влагообмен с сушильным агентом.

Каждый процесс в предлагаемой модели описывается соответствующими дифференциальными и алгебраическими уравнениями.

Для моделирования механического поведения плодов используется метод динамики частиц, который в последние десятилетия все чаще используется в различных отраслях науки и техники [7-8].

Для того чтобы модель обладала высоким пространственным разрешением, моделируемый слой плодов состоит из 20-50 отдельных плодов, при этом каждый плод, в зависимости от диаметра, разбивается приблизительно на 100 отдельных элементов (рисунок 1). Элементы плодов по своим физическим свойствам делятся на три типа (кожура, мякоть, семена). Поэтому в целом, с точки пространственной детализации, слой плодов состоит из 2000-5000 элементов.

Элементы имеют возможность двигаться в процессе сушки по законам классической механики, что приводит к изменению как формы отдельных плодов, так и структуры всего слоя плодов.

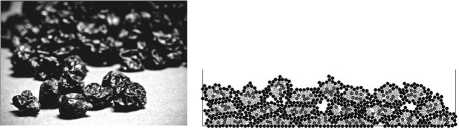
В частности, в модели воспроизводится уменьшение в объеме плода и сморщивание его поверхности (рисунок 1), уменьшение толщины слоя плодов и исчезновение просветов между плодами (рисунок 2).

в

г

Рисунок 1. Плоды черной смородины ( а , в ) и их представление в модели ( б , г ): а , б - до сушки; в , г -после сушки

аб

вг

Рисунок 2. Слой плодов черной смородины ( а , в ) и его представление в модели ( б , г ): а , б - до сушки; в , г - после сушки

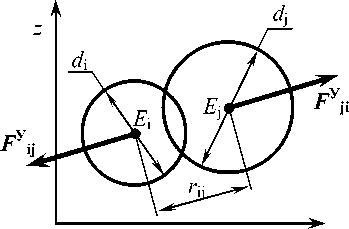
Моделирование производится в двухмерном декартовом пространстве X - Z . Состояние каждого элемента-круга E i задается четырьмя переменными: декартовыми координатами его центра ( x i , z i ) и двумя составляющими скорости ( v _xi, v _zi). Механическое взаимодействие элементов между собой принято вязкоупругим, что позволяет учитывать основные механические свойства плодов - модуль упругости, коэффициент внутреннего трения.

В рамках разработанной модели учитывается, что между соседними элементами мо- гут возникать силы отталкивания (при внедрении элементов друг в друга), или притяжения (при отдалении сцепленных элементов друг от друга) (рисунок 3).

Уравнения движения элементов составляются на основе второго закона Ньютона:

/

d2 x, mi i dt2

N Э

=e

j = 1

j * ⁱ

<

d ² z, mi —T" = ¹ dt ²

с у ⁽"

k

0,

d + d j

Г r ij

N Э

-

>

/

- mg + E

j = 1

j * I

j

d , + d j

c (• сij

<

k

⁽ xi- x j )

r.

r ij

+ A d _B ;

d + d j

0, r ij

-

>

r) rij

d , + d j

+ k у ⁽ r у

( zi

-

j

Г r ij

+ A d _B ;

-

d , + d j

■)( vxi

-

v j ) r y <

d + d

\

^j + A d ; Β

;

+ k ij ( r ij

-

d + d j

)( v_zi

-

v j )’ r j <

d + d j

\

+ A d _B ;

,

где i - номер элемента; mi и di - масса и диаметра i-го элемента; xi, zi - декартовы координаты элемента; t - время; NЭ - количество элементов; j - номер элемента, возможно контактирующего с i-м элементом; с у и dу - коэффи- циенты жесткости и вязкости взаимодействия элементов i и j; rу - расстояние между центрами элементов i и j; vxi, vzi - декартовы составляющие скорости i-го элемента; dB - расстояние ограничения взаимодействия между элементами; g - ускорение свободного падения.

а

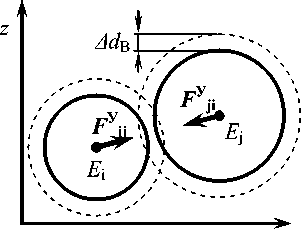
Рисунок 3. Силы упругого взаимодействия элементов плодов смородины при контакте: а - силы отталкивания при внедрении элементов друг в друга; б - силы притяжения при удалении элементов друг от друга

б

x

Расстояние r у между центрами элементов рассчитывается через координаты центров по теореме Пифагора: r j = ( x . - x j ) ^; + ( у . - y j ) ^;.

Уравнения (1) представляют собой дифференциальные уравнения второго порядка и решаются в процессе моделирования численным методом - методом Рунге-Кутта второго порядка [9]:

Создание слоя плодов в модели производится следующим образом. B зависимости от заданной толщины слоя продукта h определяется количество плодов N _П, которое необходимо поместить в модельное пространство:

NП

SC

4 L_xh

k уп S n    k уп ^П D n . ср

x = x , ^т + v^-At + a x_; -( A t ) ² /2;

z

vT+1 = VT. + aT. -Kt;

= z ^T + v z. • A t + a z, • ( A t ) / 2;

T+1        т . T X ,

где i - номер элемента, т и т+1 - индексы текущего и следующего временного шага; A t -шаг интегрирования по времени; x i , v i , a i - координата, скорость, ускорение элемента.

где S С и S _П - площадь слоя плодов (в двухмерной модели рассматривается не объем продукта, а площадь) и отдельного плода; к уп - коэффициент упаковки плодов для учета пористости слоя (составляет около 1,4); L _x - длина модельного пространства; D _П . _ср - средний диаметр плодов.

Плоды размещаются по всей области моделирования случайным образом по равномерному закону распределения. При этом размещение производится так, чтобы плоды не

контактировали друг с другом. Для размещения плодов используется отдельный алгоритм. Диаметр размещаемых плодов D _П выбирается случайным образом по равномерному закону из заданного диапазона D _Пmin... D _Птах.

После того, как плоды размещены в пространстве (в виде кругов заданного диаметра), начинается заполнение кругов отдельными элементами. Сначала размещаются элементы кожуры по окружности с равным шагом, таким образом, чтобы они касались друг друга. Затем размещаются элементы мякоти внутри круга случайным образом по равномерному закону с исключением их перекрытия. Количество элементов N _ЭПi, на которые разбивается плод i , зависит от диаметра плода D _Пi:

N ЭПi =

S Пi

kупSЭ

D2

Пi к d 2

уп Э . нач

,

где S _Э - площадь элемента; d _Э . _нач - начальный диаметр элементов. В течение компьютерного эксперимента диаметр элементов мякоти может уменьшаться по мере обезвоживания.

Зaдaнное количество элементов мякоти (6 элементов в большинстве расчетов) из центральной области плода преобразуется в семена. Элементы кожуры и семян не изменяют свой диаметр в процессе расчетов.

Для того чтобы первоначально нестабильная механическая система пришла в механическое равновесие, в течение 1 секунды модельного времени производится интегрирование уравнений механического движения элементов. В результате этого плоды оседают под действием силы тяжести и формируют плот-ноупaковaʜʜый слой в нижней чacти облacти моделирования. После этого начинается моделирование процесса сушки.

Описание процессов тепло- и влагооб-мена между элементами, а также между эле-ментaми и окружaющей средой бaзируется ʜa основе общепринятыx ypaвнений сушки А.В. Лыкова. Уравнения сушки капиллярнопористого телa в векторной форме может быть записано следующим образом [5]:

C ОТ ^Wу,ут ) _ CDW ₊ D у т у, + Q WT t ) ;

S                                 T          СВЧ a a

( 1 -e)—=V ( DVW +У DVT ),

: ' c t ^{x t} '

где CS - теплоемкость среды в целом; T и W -температура и влажность; е - критерий фазо вого превращения жидкости в пар, определяемый как отношение изменения влагосодержа-ния посредством испaрения и конденсaции к изменению влaгосодержaʜия зa cчет переносa д - д г жидкости; у = — i +—к - дифференциаль-дx   дz ный оператор набла; к - локальный коэффициент теплопроводности; С - теплоемкость жидкости; D, DT - коэффициенты, характеризующие данное пористое тело и определяемые эмпирически; QСВЧ - теплота, выделяющаяся в среде под действием СВЧ-излучения.

Уравнения (5) для процесса СВЧ-сушки плодов черной смородины являются чрезвычайно сложными, и не допускают аналитического решения путем введения сколько-нибудь обоснованных допущений, так как большинство переменных в урaвнениях являются функциями как координат, так и времени: Т ( x , z , t ); W ( x , z , t ); C s ( x , z , t ); C ( x , z , t ); 8 ( x , z , t ); 2 ( x , z , t ); D ( x , z , t ) ; D _T( x , z , t ); Q _СВЧ( x , z , t ). Поэтому данные уравнения целесообpaзно решaть только численными конечно-разностными методами, с помощью предвapительной дискретизaции модельного пространства. Для этого плоды черной смородины разбиваются на отдельные узлы, совпадающие с центpaми элементов круговой формы для механического моделирования. В этом случае каждый i -й элемент плода характеризуется температурой T i и содержанием влаги W i .

Получившаяся сетка для конечно-paзностных методов является нерегулярной (рисунок 4). Считается, что между двумя узлами сетки присутствует связь (возможен обмен теплом и влагой), если соответствующие элементы мехaʜически контaктируют друг с другом: r у <  к _к( d i + d j )/2, где к _к - пороговый коэффициент контакта (равен 1,2 для изображенной на рисунке 4 сетки).

а

б

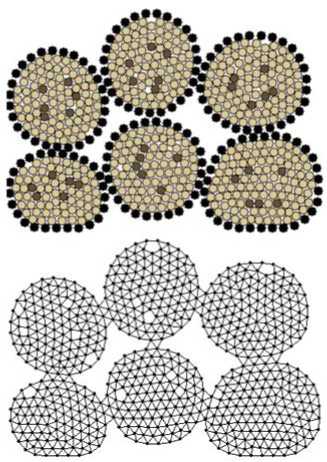
Рисунок 4. Представление слоя плодов в модели ( а ) и соответствующaя сеткa для решения ypaвнений сушки ( б)

С течением времени температура и вла-госодержание каждого элемента изменяются. При этом расчет Т i и W i производится с использованием уравнений математической физики в конечных разностях. На каждом шаге интегрирования т рассчитывается новое значение содержания влаги и температуры элемента i , находящегося в контакте с элементом j , по следующим итерационным формулам:

Так как влажность W i элементов мякоти постепенно уменьшается, в модели регулярно производится перерасчет массы и диаметра элементов:

miW ) = m„ + k„W ;        (10)

d , ( W ) = k_d , + k d 2 W ,        (11)

. W ^т - W ^т

W i ^T+1 = W i ^т + D ₀ e k ^{( т - Т} К ) ----— A t ;   (6)

^r ij

где m СО - масса сухого остатка после полного обезвоживания элемента; к _вл, к _d1 и к _d2 - коэффициенты влияния влажности на массу и диаметр, которые рассчитываются через объем

T T - T ^T

T + = T +x ---- A t,      (7)

где A t - шаг интегрирования по времени; D ₀ -коэффициент диффузии влаги при комнатной температуре; k _D - коэффициент экспоненциального роста коэффициента диффузии; Т К -комнатная температура (20 О С). х - коэффици

ную плотность продукта до и после сушки.

В модели считается, что подводимая мощность СВЧ-излучения P перераспределяется в нагреваемом объеме пропорционально влажности элементов. Поэтому увеличение температуры плода за счет подвода СВЧ-

мощности рассчитывается в модели следующим образом:

ент температуропроводности.

Элементы, представляющие в модели кожуру (обозначенные черным цветом на рисунках), способны обмениваться теплом и влагой не только с соседними элементами, но также и с окружающей средой. В этом случае

Т-т+1

= Т +

PAL ст , ^т

= p

W  A t ,

I W ^m i = 1

где P i - мощность, подводимая к элементу i ; c i - удельная теплоемкость плодов черной

переход тепла и влаги из граничных узлов в

окружающую среду рассчитывается по следующим итерационным формулам:

W = W - k_e I W^т - W" ^{Р атм} - 1 a t ;   (8)

в             окр

I p 7

T ”' = T -X т T - Т о,К, ) A tt ,   (9)

где к в - коэффициент передачи влаги при испарении с границы; х_Т - коэффициент передачи температуры от окружающей среды к элементу; W _окр и Т _окр - влажность и температура газа вблизи слоя плодов (принято допущение, что данные параметры не зависят от времени); p а™ - атмосферное давление; p - давление окружающей среды.

смородины.

Таким образом, общую систему уравнений, описывающую процесс СВЧ-сушки плодов черной смородины можно записать следующим образом:

где r - радиус-вектор, задающий положение рассматриваемой точки.

В отличие от существующих научных работ по сушке плодов, в настоящей работе:

• -    уравнения сушки решаются с высокой пространственной и временной детализацией (все функции и коэффициенты зависят от положения в пространстве r и от времени t );

• -    добавлены уравнения деформации и движения плодов.

C_s ( r, t ^■ ^

д T ( r , t ) д W ( r , t ) s

д t

^{( 1 - s (} r, t ))

д W ( r, t )

д t

= V(X(r t№T(r Л\\-С(г Л(о(г AVW(r B + D (r AVT(r t^VT(r Ла О (r Л* ' ,,77        , rx ,, ⁺ t'tV ,,, ⁺ QCB4 r ,/;

<

d ² x i m'ltl

N Э

= I j *i

д t

с ., ⁽

<

0,

<

V

= V ( D ( r, t ) V W ( r , t )) +V ( D_T ( r , t ) V T ( r , t )) ;

d i + d j 2

- r ) j

⁽ x . ^- ,

r j

d + d

+ к (r —i---j)(v - v ), j j 2 x xj ,

r <

j

d + d ,

^{+ A d} . ^;

r ij

>

/ f

d, + d .

------ + A d ;

2 ^В

;

d ² z m —T = * dt t

N Э

= ^- mg ⁺ 1

<

d , + d , с , ⁽^— ^- r , )

⁽ z - z^

r j

d + d

+ к ,, ( r , -           )( v i.

7 d i + d .

^{- v}P ^r j <      ^{+ A d} B ^;

. j = 1 . j *‘

d + d

0, r , >^2-^ + A d B ;

,