Разработка математической модели вулканизации двухфазных полимерных систем

Паршута Д.О., 2013

систем уравнений для образцов с разным содержанием ИВ и вулканизующей группы, а решение обратной кинетической задачи не возможно без опоры на вычислительный эксперимент. Предварительное исследование различных моделей кинетики вулканизации при помощи ЭВМ позволяет эффективно спланировать лабораторный эксперимент для создания адекватного описания процесса вулканизации, учесть сложные эффекты образования наполнителем взаимопроникающих сетчатых структур выше порога перколяции и обеспечить уверенное выделение моделей, отвечающих ведущим процессам в нелинейной динамической системе химической природы.

Существующие методы измерения кинетики вулканизации резин основаны на предположении о пропорциональности концентрации поперечных связей модулю сдвига. Поэтому при анализе кинетики вулканизации единичного образца можно получить информацию об усредненной плотности поперечных связей. Кинетика сшивания каждой из фаз может быть рассчитана только в ходе совместного решения систем уравнений для образцов с разным содержанием крошки и вулканизующей группы. С целью упрощения модели в работе использовались ИВ и резиновая смесь, изготовленные по одному рецепту и, следовательно, каучуки в обеих фазах обладали оди- наковой реакционной способностью, что позволяет объяснить различия в скорости сшивания фаз при вулканизации различиями в исходных концентрациях вулканизующих веществ.

Сложная форма зависимости концентрации от времени предполагает ингибирующее влияние промежуточных веществ на скорость образования вулканизационных связей. Наиболее вероятные механизмы реакций определялись по методике систематического кинетического анализа исходя из общей схемы возможных химических реакций, происходящих при вулканизации [1] с учетом концентрации эластичного наполнителя и вулканизующих агентов. Для фазы резиновой смеси:

ДБТД —+ S 8 — МБТ - S ₈ - МБТ — ^Каучук >

V        С              ^- • S y ^{- МБТ} х V        • *

Каучук - Sx - МБТ ------ -----> Каучук - Sz

+ Каучук

Каучук - Sz - Каучук

Каучук - S*z — — ДБТД —> Каучук - Sz - МБТ

Для фазы эластичного наполнителя:

МБТ — S + znO — мбт - s - zn - Мт — Каучук — 8

v        с 7            - • Sy - Zn - ^МБТ х

Каучук - Sx - Zn - Мбт------ ------->

Каучук - S* _z — ^{+ Кауч} у ^к —> Каучук - Sz - Каучук

Каучук - S*_z —^+М Б^Т —> Каучук - Sz - МБТ

В связи с этим нами была исследована модель серной вулканизации на основе схемы химических реакций протекающих параллельно в двух фазах:

A₁ —— B₁ — k² — B₁ * —— a-Vu₁

A₁ + B₁* — k⁴ — р-B₁

A₂ —— B ₂ —^— B 2 * ——— a ' - Vu ₂

A2 + B2* ——— в- B2            , где Аi – вулканизующий агент (МБТ-S8-МБТ или МБТ-S8-Zn-МБТ); Вi – продукт его взаимодействия с каучуком (Каучук-Sх-МБТ); Bi* – пертиильный радикал (Каучук-Sz٠); Vui – тетра-функциональный узел вулканизационной сетки (Каучук-Sz- Каучук); а в -стехиометрические коэффициенты. Индексы 1 и 2 соответствуют компонентам дисперс- ной среды и дисперсной фазы. Диффузия молекул вулканизующего агента в двухкомпонентной системе с химическими превращениями зависит от разности концентраций и скорости химических реакций:

\ ^ = ^- D ^- F ^- ( [ A i ] ^- [ A 2 ] ) ^- Z ^k - [ A i ]

^{d T}                                     i = 1.4             , (3)

d ^ = D - F - ( [ A i ] - [ A 2 ] ) - Z k /[ A 2 ]

^dT                                  i = 1,4

где D – коэффициент массопередачи; F – площадь раздела фаз, пропорциональна массовой доле ИВ; [ A 1 ] и [ A 2 ] – концентрация вулканизующего агента в резиновой смеси и частицах вулканизата соответственно; k _i и k _i '– константа скорости реакции c участием вулканизующего агента в фазах резиновой смеси и вулканизата.

В модели принято допущение, что для небольших концентраций низкомолекулярных веществ равновесные концентрации компонентов в фазах не зависят от степени сшивания фаз, а скорости диффузии высокомолекулярных веществ пренебрежимо малы.

Предполагалось, что механическое поведение исследуемой двухфазной системы описывается с помощью простых моделей, состоящих из двух компонентов с различными модулями упругости. Например, модуль сдвига G , определяющий величину крутящего момента при испытаниях на реометре, подчиняется уравнению Takayanagi [2]:

( 7----------------+(l-Vl 'I

((1 - 4)-G1 + 4-G 2     G 2 '

где G₁ и G₂ - модули упругости компонентов – дисперсной среды и фазы, соответственно; Ф ^ Х - объемная доля дисперсного компонента в смеси.

Модуль сдвига при температуре испытании пропорционален сумме физиче-ск их и химических связей. Из уравнения (4) видно, что для такой модели модуль сдвига смеси G будет монотонно изменяться от G₁ к G 2 с ростом концентрации дисперсной фазы.

Исследования исходной наполненной техническим углеродом П-234 смеси на основе каучука СКС-30 АРК проводили на реометре Monsanto-100S. Значение крутящего момента М при температуре вулканизации пропорционально коэффициенту С1 в уравнении Муни – Ривлина [4], его изменение хорошо описывает кинетику формирования сетки вулканизационных связей. Полученные кинетические кривые роста крутящего момента во времени хорошо описываются уравнениями Корана (1) для смеси без резиновой крошки, но применение только уравнений Корана для описания кинетики вулканизации наполненной крошкой композиции не приводит к удовлетворительному соответствию модели экспериментальным данным.

В ходе вычислительного эксперимента был исследован ряд моделей. На рис. 1 представлены результаты моделирования для двух моделей, различающихся одним параметром – коэффициентом массопереноса между фазами.

Анализируя кинетические кривые для композиции Км можно сказать, что модель (б), учитывающая диффузию вулканизующих веществ, позволяет точнее описать особенности вулканизации исследованных смесей.

Решение обратной кинетической задачи для реакции серной вулканизации композиций, наполненной 0 - 50 масс.ч. измельченного вулканизата с размером частиц 0,25 - 0,50 мм, проводилось методом минимизации Пауэлла с ограничениями, вводимыми путем добавления соответствующих штрафных функций к минимизируемому функционалу [5]:

N

ф ( k ) = Z W i ^ j , ' J- * ,02 i = 1 j , (5)

где N = 9 – число экспериментов, проведенных при различных концентрациях измельченного вулканизата; x ij (t j ) – экспериментальные значения; y ij (k,t j ) – рассчитанные значения модуля сдвига; w i – весовые коэффициенты.

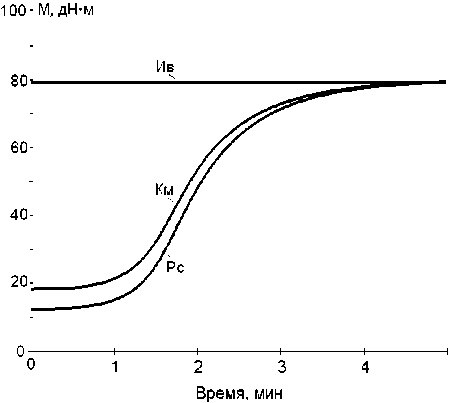
а

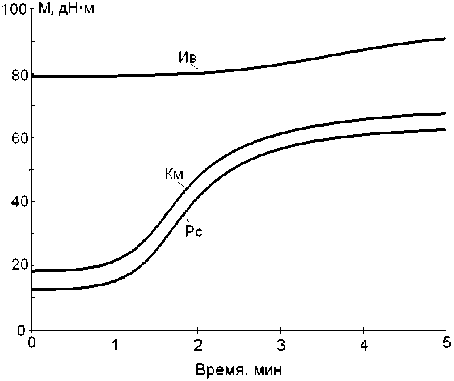
б

Рис. 1. Кинетика структурирования для моделей композита, наполненного 20 масс.ч. измельченного вулканизата : а – в отсутствие массопереноса, ( D = 0) и б – в условиях массопереноса ( D = 1): Ив – степень структурирования измельченного вулканизата ; Рс – резиновой смеси ; Км – средняя степень сшивания композита, в относительных единицах, приведенных к реометрической кривой для резиновой смеси.

Интегрирование системы ОДУ проводили методом Рунге – Кутта 5 порядка. Приведенное на рис. 2 решение системы уравнений (1- 4) для смеси, содержащей 20 масс. ч. измельченного вулканизата адекватно описывает экспериментальные данные (критерий Фишера, F = 235.3).

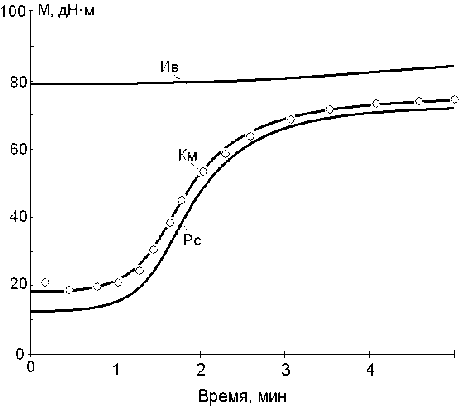
Рис. 2. Кинетика серной вулканизации композиции из СКС-30АРКП при 463 К, наполненной 20 масс.ч. измельченного вулканизата. ° - экспериментальные значения, Ив – степень структурирования измельченного вулканизата ; Рс – резиновой смеси ; Км – средняя степень сшивания композита.

Модель, учитывающая диффузию вулканизующих веществ между фазами композиционного материала, позволяет адекватно описать экспериментальные данные, полученные на реометре. Средние относительные отклонения между моделью и экспериментальными значениями не превышают 2 %.

Т а б л и ц а 1

Эффективные значения констант скорости вулканизации стандартных резин на основе СКС-30АРКП при 463 К '

Содержание ИВ мас. ч.	k 1	k2	k 3	k4
	k 1 ' *	k 2 '	k 3 '	k 4 '
0.0	0.216	2.49	20.9	249
	–	–	–	–
5.0	0.116	2.56	20.3	350
	0.117	1.96	17.3	358
10.0	0.127	2.74	20.8	379
	0.157	2.27	15.3	392
20.0	0.114	2.77	20.0	320
	0.083	2.42	17.8	350
50.0	0.074	3.05	20.3	369
	0.102	3.00	19.6	477

Проведенный качественный анализ модели позволил выявить механизм ускорения процесса вулканизации резиновых смесей в присутствии ИВ. Установлено, что в процессе вулканизации происходит формирование неоднородной структуры химической пространственной сетки вблизи частиц измельченного вулканизата.

Исследования модели показали, что при исходном градиенте концентрации вулканизующих агентов между фазами и близких константах скорости, степень вулканизации дисперсной среды оказывается ниже, чем в отсутствии диффузии. Скорость сшивания ИВ меньше среднего значения, но степень сшивания в конце процесса вулканизации оказывается выше. При этом средняя степень сшивания всей системы ( К _м) возрастает медленнее, чем при вулканизации в отсутствие диффузии вулканизующих веществ, а скорость вулканизации и общая степень сшиваниия композита в целом снижается.