Разработка математической теории внутренних гравитационных волн в узких глубоких водоемах переменной ширины

В узких глубоких водоемах переменной ширины теория внутренних гравитационных волн основана на компактных краевых задачах математической физики, имеющих следующий вид

0²<Д , O²0i , 1 DB1D01 , 1 DB1D01 _п

9ж² Oz²     Bi Ox Ox Bi Oz Oz ’       ^{1 2} " '

^  D²0₂   1 0B₂ N2   1 0В₂0ф₂               _

9ж²     Oz²   B₂ Ox Ox   B₂ Oz Oz

-^_r+g— = 0 npnz = h₂;                  (3)

f^2 , N2\ NN2 , N2\ _ ~ п

Pi              = £1 "ТТг + Ац— при z = 0;

\ Ot² Oz у \ W Oz у

N1 1)ф2

• — = — при z = 0;

Oz Oz

• —— = 0 при z = —hi;                          (6)

где ф1 и ф₂ потенциалы скоростей на нижнем и верхнем слоях соответственно, pi и р₂ — плотности Bi = В1(ж,Й и В₂ = В₂Д,1^ — ширина нижнего и верхнего слоя водоема, g — ускорение силы тяжести, hi и /12 — глубины слоев.

В классической теории внутренних гравитационных волн скорости удовлетворяют дифференциальному уравнению Лапласа. Здесь же дополнительно вошли два слагаемых. Они связаны с непризматическим очертанием водоема. Поставленная контактная краевая задача решена следующим способом. Функции ф1Д,г,^ и ф2Д,г,1^ представлены в виде следующих зависимостей ф1 (ж, z, /) = ф1 (2:)sin kxcos ot,(7)

Ф2Д, z, t) = V’2(^)sin kxcos ot.(8)

Подставив эти выражения в (1)—(6), получим

^ + s * -    = 0.(9)

dz2 az

• (с) 1999 Музаев И. Д., Хубежты Ш. С.

• <^2 X           / 2 / п    о // г

  
  

, „ + s₂ —-- К ^2 = 0,    О <  Z < /1₂;

0,7/O.Z

-а2^2(^) + У-^ = ° при z =/i2;(И)

(   2 х . Nl\ /   2 , , х .^2 А при z = 0;          (12)

Р1 -СТ № + д^— = Р2\-СТ Т^) + д—— \              az /      \              az / где

1/>₂(г) = С₃е^Л1² ^С^\

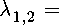
4 ’

"

1,2

ч2

^ + т-

Ni N2        „ — = —— при z = 0; az    az	(13)
—— = 0 при z = —h4-, az	(14)

Общие решения дифференциальных уравнений (9)-(10) имеют следующие вид

№) = Ciexiz +С2е^-\

(15)

Постоянные C*i, С₂, С₃ и С₄ определяются с помощью граничных условий (11)—(14). Подставив в эти граничные условия выражения (15) и (16), получим однородную систему алгебраических уравнений

(-ст²е^{Л1 h}- + gXJ^Ca + (,-о²е^х- ^h- + дХ^е^- ^h^C₄ = 0,

k-Pio² + P^AJCx + (-р₂а² + pigX^C₂ + Д₂о² - р^дХ^ )С₃ +

+ (^га2 — р^дХДС^ = 0,(20)

а'1С1 + А2С2-А'1'Сз-А2С4 = 0,(21)

А'^-^/и^! + x^e-^-h^C2 = 0.(22)

Очевидно, что для существования нетривиального решения системы (19)—(22) ее определитель должен равняться нулю. В результате приравнивания нулю определителя этой системы получаются частотные уравнения вида

(акт2 + Ь^Д2а2 + 62) - (а3а2 + b^a2 + b^ = 0,(23)

где ах = -е^ Ь1 = g\^h\ а2 = рД, Дхе"х* - А'е"^) + р2к2^"^ - е"^^ ),

Ъ2 = gk\pi - р^Х2<е"х^ - е"^, а3 = -exih\ b3 = gX2ex'^h-,                         (24)

а4 = щА^'(А^е-^711 - A^e"^711) + p2k2lyTxihl - е"^711), b4 = дк2Д1 - p2)Xi(e"Xlhl - e"A^1).

Частота колебания поверхности раздела легко определяется из алгебраического уравнения (23). Однако зависимость для частоты получается весьма громоздкой, и ее анализ крайне сложен. В связи с этим принимаются определенные упрощающие допущения.

При hi —> оо и h₂ —> ос получается

/а\ ² _ Д1 — P2^s₂ + 2t/₂) + pi(si + 2di) + p2^—s₂ + 2t/₂)

Vk) ⁹         Pi^si + 2di)(s₂ + 2d₂) + 4p2k²

хДкрТ-^^^зТ^ДМ^-^ДзТ^Д^сГ^ s2 + 2^2)]2       /2^\ j°i(si + 2t/i)(s2 + 2t/2) + 4p2k^

4(pi — /^Hpifsi + 2di)(s2 + 2d₂) + 4/?2&²]

jOi(si + 2di)^S2 + 2^2) + 4p2k²

При si = 82 = 0 получаем

(lA^⁹-⁹!^!.                    (26)

V к / к pi + P2

Эта зависимость представляет фазовую скорость внутренней гравитационной волны. Рассмотрим вторую задачу.

---= 0 при 2 = /i2;(29)

^>Ф1 О

—— = О при z = —hi.(32)

Эта задача от предыдущей отличается тем, что верхняя граница верхнего слоя представляется жесткой и непроницаемой. В предыдущей задаче она представляла свободную волновую поверхность.

Для фазовой скорости внутренней волны получена следующая формула

=(^У = ----........... . (33)

\k ) Pi(si + 2Д cth (c?i/ii)) + Р2^-32 + 2d₂ Cth фЫ^

Эта формула представляет собой обобщение для непризматического водоема широко известной формулы для фазовой скорости с2 = 9т Р-^.                           (34)

к Pl - Р2

которая получается как частный случай из выражения (33) при hi —> оо и /12 —> оо.

В третьей задаче учитывается непризматическое очертание водоема как в вертикальном направлении, так и в продольном направлении. Краевая задача имеет следующий вид:

^Ф2 , ^Ф2 , Ш ,  ^2      п W * ЭД       +S2 Dz "°’  °' Ф2 ^>Ф2 _2 +9    = ° ПРИ 2 = ^2! W2 , NA        , n2\ Pl 1 _,2 । 0       ) — Р2 1         + 9 _ 1 \ ЭД     Эг У     \ ЭД     Эг У — = — при z = 0; ---= 0 при z = —hi. Изменения ширины водоема учитывается по зависимости В1(ж,г) = Вое5$+51ф

^zCh2;             (36) (37) при z = 0;              (38) (39) (40) (41)

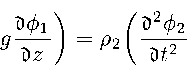
B₂(x,z) = B₀e^sx+S2Z.                             (42)

Представленные краевые задачи имеют как теоретический интерес, так и практический. Практическое значение обусловлено тем, что в селективных водозаборных сооружениях имеют место слоистые течения воды с внутренними гравитационными волнами. Для обеспечения устойчивости поверхности раздела осветленной и мутной слоев воды необходимо проведение вышеприведенного анализа.