Разработка метода неинвазивного измерения расхода жидкости и газа через стенку трубопровода

Важнейшей задачей в механике жидкости и газа является определение характеристик турбулентного течения по параметрам акустического сигнала. Турбулентность является сложным физическим процессом и к настоящему времени имеет много нерешённых вопросов, в том числе одним из них является математическое описание процесса диссипации турбулентных вихрей в пограничном слое.

С практической стороны важность исследования обусловлена современными тенденциями в приборостроении, направленными на энергоэффективность и снижение затрат. В настоящее время широкое распространение получили неинвазивные методы измерения расхода жидких и газообразных сред в трубопроводах. Это является следующим витком в развитии средств измерения.

Одним из таких перспективных устройств является накладной гидроакустический расходомер, определяющий расход по характеристикам турбулентных вихрей в пограничном слое. Предлагаемая технология позволяет определять параметры турбулентного течения в пограничном слое через твердую стенку, в том числе измерять объемный расход жидких, газообразных и мно-

Кривоногов А.А., Разработка метода неинвазивного измерения Гонтарев К.А. расхода жидкости и газа через стенку трубопровода гокомпонентных сред без врезки в трубопровод и без перекрытия потока. Разработанное решение повышает безопасность, поскольку нет повреждения трубопровода от врезки расходомера, снижает потери при транспортировке продукта, поскольку нет препятствия потоку. Дополнительно имеется возможность переустановки на различные участки трубопровода без остановки потока, не требует остановки процесса при поверке.

Основной проблемой в создании накладного акустического расходомера является математический метод обработки выходного сигнала, позволяющий выделить полезный сигнал из набора шумов, приходящих от сенсоров, и определить фазовую скорость перемещающихся вихревых полей, которая соответствует скорости потока среды в трубопроводе, а из скорости потока вычисляется объемный расход.

К настоящему моменту эту технологию исследует американский ученый Dr. Daniel L. Gysling. Он имеет ряд научных публикаций [1, 2] и патентов на изобретения [3], в которых говорится о возможности измерения конвективной скорости потока через стенку при помощи пьезопленочных сенсоров. При этом нет явного описания физического процесса, на базе которого реализован данный способ измерения, а также подробного описания метода обработки сигнала. Известно только то, что в основе способа измерения расхода лежит гипотеза Дж. Тейлора о «замороженной турбулентности», при этом не раскрыты методы обработки сигнала и параметры этого физического явления. Однако на базе его патентов две западные компании – Cidra и Expro предлагают на рынке расходомеры, работающие на вышеизложенном принципе.

В книге профессора ЦАГИ д.т.н. А.Ю. Голубева [4] представлены существующие методы построения структуры поля пристеночных пульсаций давления в виде частотно-волновых спектров, но нет описания методов измерения пульсаций давления через стенку и фильтрации полученного сигнала.

В связи с вышеизложенным создание метода определения параметров турбулентного течения по значениям акустического сигнала и устройства для определения объемного расхода на его основе является актуальной задачей.

Разработка метода неинвазивного измерения расхода

В предлагаемом методе физическим носителем полезного сигнала являются турбулентные вихри, находящиеся в пограничном слое [5]. В процессе движения по течению они переносятся со средней скоростью потока. Вихри пульсируют, двигаясь по потоку, и распадаются на более мелкие составляющие.

В основе метода заложена гипотеза о «замороженности турбулентности» Тейлора [6], которая гласит, что скорость конвекции турбулентных вихрей U_c не зависит от пульсационной составляющей u’ ( t ) и равна средней скорости потока. Таким образом, зная частоту пульсаций вихря – f и волновое число – k , можно определить скорость турбулентной конвекции или фазовую скорость:

U c = f / k . (1)

В качестве источника сигнала используются вихри, движущиеся в пограничном слое или вблизи него в турбулентном потоке, которые можно определить как мгновенное значение давления:

P ( x , t ) = P ( x ) + p ( x , t ), (2) где P ( x ) – статическое давление , p ( x,t ) – центрированная функция, описывающая случайные по пространству и времени пульсации давления, которая, в свою очередь, может быть представлена в виде суммы гидродинамической p ( x,t ) гд , акустической p ( x,t ) ак и остальных составляющих пульсационного давления p ( x,t ) др :

• P ^{( x} , t ) = P ^{( x} , t ) гд ⁺ P ^{( x} , t ) ак ⁺ P ^{( x} , t ) др . ⁽³⁾

Для измерения объемного расхода полезным источником сигнала является гидродинамическая составляющая p ( x,t ) гд пульсирующего давления, поскольку конвекция вихрей происходит именно в этой области сигнала. Однако простого считывания сигнала в точке недостаточно, потому что для вычисления скорости конвекции необходимо определить параметры конвертирующего вихря, такие как частота пульсаций вихря – f и его волновое число – k . Для этого применяется пространственная спектральная обработка.

Механика

В соответствии с вышеизложенным метод [7] реализован в виде функциональной схемы, представленной на рис. 1. В качестве источника полезного сигнала выступают турбулентные вихри поз. 1 , конвертирующие в потоке измеряемой среды. Сигналы, получаемые с датчиков поз. 2, подвергаются пространственной (волновой) фильтрации, затем частотной (полосовой). Далее на вход К-Омега модуля обработки сигнала поз. 3 поступает отфильтрованный сигнал со всех сенсоров одновременно, содержащий з начения пульсаций давления турбулентных вихрей p ( x,t ) гд в конвективной области спектра, где его подвергают частотно-волновой обработке по зависимости:

M - 1 N - 1

• 5 ( k , f ) = 717 I Z p ( X m , t n ) e "f^N + k^M ) ,                      (4)

^MN m = 0 n = 0

где S - частотно-волновой спектр, k - волновое число, f - частота, N - количество отсчетов, M - количество сенсоров, p - набор сигналов (двумерная матрица) с сенсоров после фильтрации, n - строки, m - столбцы, x - расстояние между сенсорами, t - время.

Q - объемный расход Т|-----------------------—

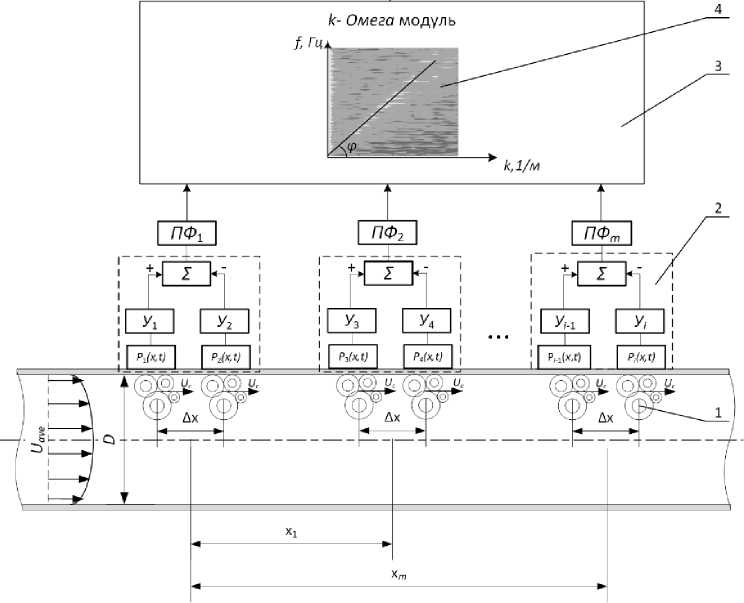
Рис. 1. Функциональная структура метода неинвазивного измерения расхода

По результатам обработки строятся двумерные графики частотно-волновых спектров поз. 4. Каждая точка, лежащая на вершине фронта, определяет скорость конвекции вихря своего масштаба. Тем самым можно определить скорость конвекции вихревого поля в потоке, а не отдельной волны. Для этого выполняется линейная аппроксимация значений фронта конвективных максимумов и определяется угол наклона ф линии фронта, значения которого передаются в модуль поз. 5, где можно вычислить скорость конвекции вихрей U c . Зная скорость конвекции, возможно вычислить среднюю скорость потока U_cp через передаточный коэффициент у , а по средней скорости вычислить объемный расход Q :

UCPD D yUcnD2 _ prD2 tg(^)

4    =     4

Q = —--

Таким образом, работает метод неинвазивного определения объемного расхода жидкости и газа в трубопроводе на основе пространственно-временной фильтрации и частотно-волновой обработки сигнала.

Кривоногов А.А., Гонтарев К.А.

Численные исследования

С целью определения оптимальной конфигурации опытного образца и уменьшения количества паразитных параметров, влияющих на полезный сигнал, построена его имитационная модель.

Моделирование выполнено в двумерной постановке в программной среде ANSYS CFX. Расчетная область представляет собой плоский канал длиной 1 метр, высотой 14 миллиметров с заданными условиями симметрии [8]. Таким образом имитируется плоский канал бесконечной ширины. Тем самым возможно получить течение жидкости вдоль плоской поверхности. Модель турбулентности SBES (scale based eddy simulation) [9] позволяет моделировать турбулентные пульсации давления и скорости в потоке, не осредняя их полностью. В результате получается пульсирующее течение, при этом не требуется сетка высокой плотности в параллельных стенке канала координатах, как для LES модели турбулентности.

Для исследования влияния количества сенсоров и расстояния между ними было построено 4 расчетных модели (рис. 2), отличающихся количеством точек записи пульсаций давления и расстояния между ними.

Первая модель (рис. 2, а) содержит 36 расчетных точек, расположенных вдоль оси канала с шагом 9 миллиметров. Построена с целью максимального разрешения полей пульсаций давле- ния.

Вторая, третья и четвертая (рис. 2, а, б и в) модели содержат 8 точек записи сигнала с шагом 9, 18 и 36 миллиметров соответственно. Таким образом, можно оценить влияние количества сен- соров на качество получаемого частотно-волнового спектра.

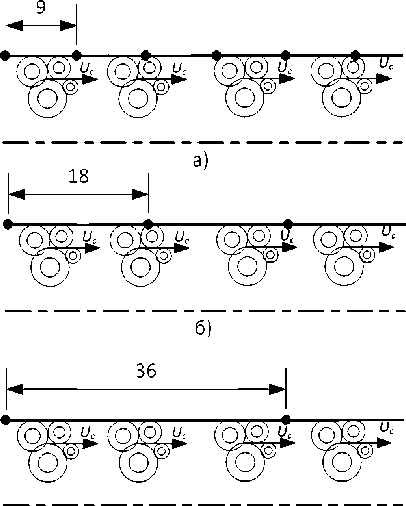
в)

Рис. 2. Расчетные модели в ANSYS CFX

В процессе моделирования для каждого расчетного случая записано по 5 000 отсчетов (сэмплов) с шагом по времени 0,0005 с. Расчеты выполнены для скорости потока 5 м/с, поскольку при наибольшей скорости потока достигается максимальная амплитуда пульсаций давления. Это позволяет точнее определять конвективные характеристики турбулентного течения относительно паразитных шумов.

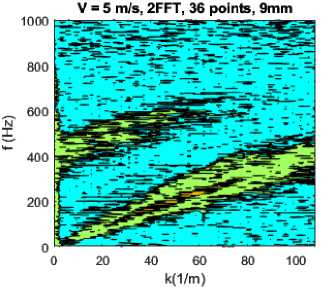
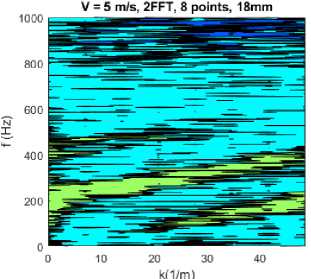
По результатам обработки по вышеизложенному алгоритму построены двумерные графики частотно-волновых спектров (рис. 3).

На рис. 3, а представлены результаты моделирования для первого расчетного случая – 36 точек с шагом 9 мм. На графике частотно-волнового спектра отчетливо виден конвективный фронт, угол наклона которого соответствует средней скорости потока в канале. Если разделить значение частоты на волновое число для точки, лежащей в границах конвективного фронта, то получим скорость набегающего потока. Например, 200 Гц/40(м^–1) = 5 м/с.

На рис. 3, б представлен график для второго расчетного случая, на котором конвективный фронт получился с более низким разрешением за счет меньшего количества точек – 8 штук.

На рис. 3, в и г представлены графики для третьего и четвертного расчетных случаев – 8 точек записи с шагом 18 и 36 миллиметров соответственно. На графиках видно, что при увеличении расстояния между точками записи (сенсорами) разрешение по волновому числу снижается за счет увеличения минимального значения волнового числа k. Однако конвективный фронт при- сутствует также, но в связи с увеличением расстояния между сенсорами возникает вторичный конвективный фронт. Соответственно, на графиках с большим расстоянием между сенсорами виден «хвост» нижнего конвективного фронта.

Механика

а)

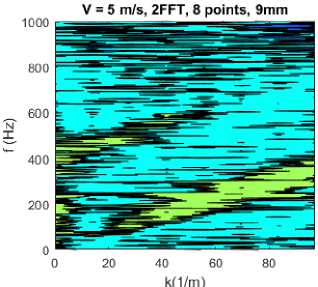
в)

Рис. 3. Частотно-волновые спектры расчетные

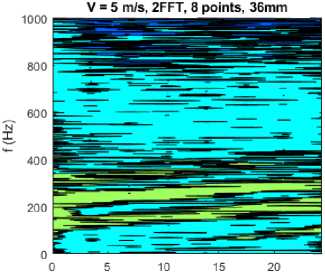
кН/m) г)

устранения ступенчатого отображения конвективного фронта по волновому числу.

При этом угол наклона сохраняется постоянным, что позволяет определять скорость конвекции вихрей.

Таким образом, по результатам моделирования установлено, что для корректной частотно-волновой обработки достаточно 8 сенсоров (точек) с расстоянием 36 мм для точного определения конвективного фронта, однако требуется модификация метода обработки с помощью применения двумерной спектральной обработки по времени и по пространству (k-omega beamforming). Переход от линейной частоты и волнового числа к угловым параметрам для

метода, представленного в разделе 2.

Натурные испытания

Испытания проведены на проливочной установке МЕТРАН – УПА – 2000. Проливка выполнена на пяти скоростях потока от максимальной 10 м/с до минимальной 1 м/с, чтобы понять, какую чувствительность обеспечивает прибор на различных скоростях потока.

Конструкция измерительной части содержит восемь анизотропных пьезопленочных сенсоров, прижатых хомутами к наружной стенке проточной части номинальным диаметром 100 мм. Благодаря этому обеспечивается плотный контакт с поверхностью. Далее с помощью экранированного кабеля сигналы передаются на восьмиканальный осциллограф Tektronix MSO 5B (рис. 4). Сигналы записывались на флэш-накопитель для последующей обработки с помощью

По результатам испытаний построено пять двумерных контурных графиков (рис. 5).

Поскольку полезный сигнал расположен в низкочастотной и коротковолновый части турбулентного спектра, он отфильтрован по длине волны больше 360 мм и по частотной полосе от 10 до 300 Гц. Соответственно после волновой обработки остается 7 точек

Рис. 4. Испытания опытного образца с осциллографом

для    построения    частотно волнового спектра, поскольку удаление длинноволновых пульсаций выполняется путем вычитания сигнала с одного сенсора из другого (см. рис. 1). Для обработки взято 100 тысяч отсчетов (сэмплов) с интервалом записи 0,00001 с, таким образом, время записи сигнала составило 1 с.

Как видно из результатов испытаний, на скоростях потока 10 и 8 м/с отчетливо наблюдается конвективный фронт, который соответствует скорости потока (показано черной линией). Если

Кривоногов А.А., Разработка метода неинвазивного измерения

Гонтарев К.А. расхода жидкости и газа через стенку трубопровода поделить частоту на волновое число, которые соответствуют точке, лежащей на этом фронте, то получаем скорость конвекции (переноса) вихревых полей в потоке и соответственно скорость потока. Например, для первого графика частота 100(Гц)/10(1/м) = 10 м/с, что соответствует ско- рости потока.

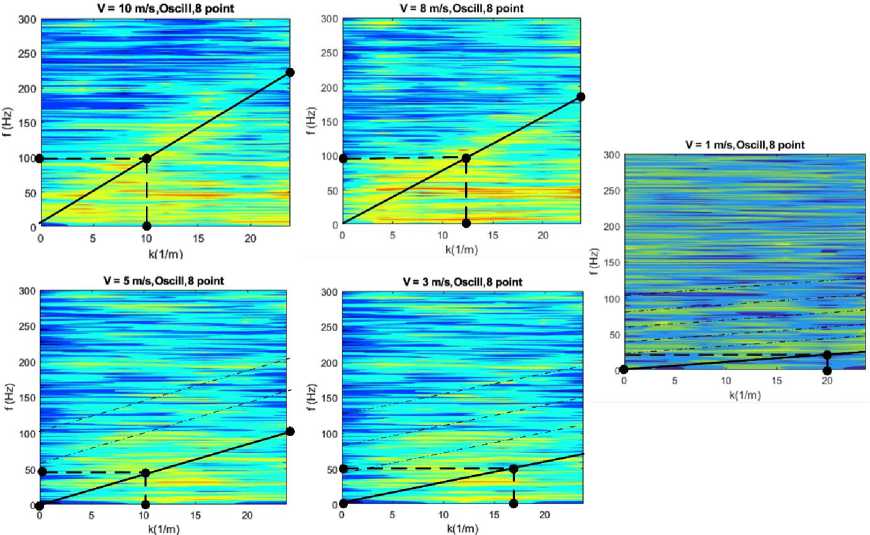
Рис. 5. Результаты испытаний с осциллографом

Однако на более низких скоростях потока 5, 3 и 1 м/с картина не так однозначна, как для 10 и 8 м/с. Связано это с несколькими факторами. Основной фактор – это применение частотноволновой обработки в линейных координатах по частоте и волновому чиcлу, в результате чего полосы по волновому числу не хватает для непрерывного отображения конвективного фронта. Получается ступенчатый конвективный фронт (обозначено тонкими штрихпунктирными линиями). Более отчетливо этот эффект виден на частотно-волновых спектрах, полученных при помощи моделирования (см. рис. 3), поскольку там нет помех и сигнал идеально чистый. Видно, что если сопоставить эти ступенчатые линии последовательно, то получится картина, как на рис. 1, там фронт непрерывен, потому что полоса по волновому числу шире. Таким образом, в следующей версии алгоритма будет применена частно-волновая обработка в угловых координатах (k-omega beamforming) с учетом мнимой и действительной частей турбулентного спектра.

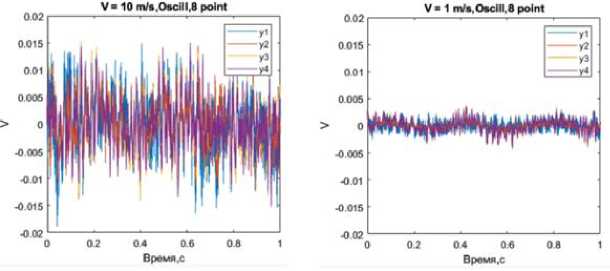
Рис. 6. Сигналы с осциллографа для скорости потока 10 м/с и 1 м/с

Вторая причина неявного отображения конвективного фронта связана со снижением энергии вихревого потока при снижении скорости. Уровень сигнала пропорционально снижается. На рис. 6 представлены два графика с сигналами для скорости 10 м/с и 1 м/с. Видно, что уровень сигнала снижается примерно в 10 раз.

Третья причина – это разная амплитуда сигналов, при- ходящая с пьезопленочных сенсоров, в связи с чем требуется приведение всех сигналов к одинаковому уровню. В данном случае сделано приведение по максимальному значению выборки по первому сенсору.

Механика

Заключение

По результатам моделирования установлено, что при использовании частотно-волновой обработки для точного определения конвективного фронта достаточно 8 точек с расстоянием 36 мм. Установлено, что расстояние между сенсорами не влияет на результат обработки, но конвективный фронт отображается ступенчато, поскольку ширины полосы по волновому числу недостаточно для непрерывного отображения конвективного фронта. Таким образом, требуется модификация метода обработки с помощью применения двумерной спектральной обработки по времени и по пространству (k-omega beamforming). Необходим переход от линейной частоты и волнового числа к угловым параметрам соответственно.

По результатам натурных испытаний опытного прототипа накладного акустического расходомера установлено, что разработанный математический метод позволяет определять объемный расход жидкости и газа в трубопроводе на основе пространственно-временной фильтрации и частотно-волновой обработки сигнала. В качестве источника полезного сигнала выступают турбулентные вихри, конвертирующие в потоке измеряемой среды. Однако предлагаемый метод необходимо модифицировать путем перехода от линейных величин k – f к угловым k –омега.

Таким образом, подтверждена справедливость гипотезы Дж. Тейлора «о замороженной турбулентности» для определения конвективного фронта в трубопроводе. При этом требуется проводить дальнейшие исследования с целью определения ограничений по минимальной скорости потока, при которой гипотеза будет справедлива.

Исследование выполнено за счет гранта Российского научного фонда № 23-29-10151,