Разработка метода расчета пластинчатого скребкового теплообменного аппарата

Основной целью расчета пластинчатого скребкового теплообменного аппарата для вязких продуктов является определение температуры продукта на выходе из каждого теплообменного элемента и расчет их количества. Температура на выходе из аппарата является заданной величиной. Расчет количества теплообменных элементов завершаем после достижение заданной температуры продукта на выходе из аппарата.

Теплообменные элементы в аппарате устанавливают последовательно, образуя поверхность теплообмена с каналами, по которым движется продукт. В зависимости от конструкции теплообменный элемент может быть с центральной и периферийной подачей продукта в него, а также с ножами-мешалками, расположенными на дисках или крестовинах (рис. 1 ) [1].

Расчет скребкового пластинчатого теплообменного аппарата проводим по следующей методике:

• -    задаем производительность аппарата;

• -    принимаем начальную и конечную температуру продукта в зависимости от технологической задачи.

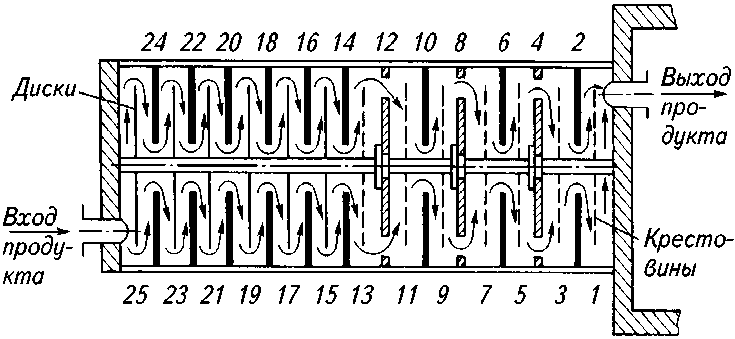
Рис. 1. Схема движения продукта в аппарате

Для проведения расчета температуры продукта на выходе принимаем следующие допущения: геометрические форма и размеры теплообменного элемента одинаковы; распределение температуры в продукте равномерное и не зависит от способа его подачи в теплообменный элемент (периферийная или центральная подача) и от конструкции ножей, расположенных на диске или на крестовинах. Расчет проводим для теплообменного элемента – охладителя. Расчетная схема для определения температуры продукта при его течении в продуктовых каналах аппарата показана на рис. 2.

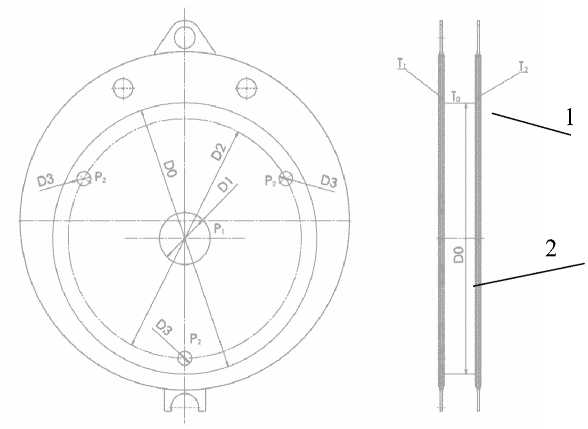
Рис. 2. Расчетная схема: 1 - теплообменные пластины; 2 - продукт; D0 - размер, ограничивающий продуктовую зону, D0=2R0; D1 - диаметр входного отверстия, D1=2R1; D2 - диаметр, на котором расположены выходные отверстия, D2=2R2; Р 1 - давление продукта на входе в теплообменный элемент; Р 2 - давление продукта на выходе из теплообменного элемента, T₀ - температура продукта; Т₁ - температура пластины 1; Т₂ - температура пластины 2

Для расчета температуры продукта на выходе из каждого теплообменного элемента используем уравнения(1), (2) и граничные условия (3):

Решение уравнений (1) и (2) при граничных условиях (3) имеет вид

д T     д T

< д2 T 1 д T д2 T )

vr — + vz — = a —7 + + —7 , дr     дz    (дr2 r дr дz2 v

д r

д z

где T – температура в точках продукта, ºС ; r , z – цилиндрические координаты точки про-

T(r,z) = -nL-l-kk[71 -T3 -(T -74)coskn][r2 -R2 -1^(r4 -R4)-2A2h22lx A h k =1 I                                  I 2 Ahk k2 n2 (R2_r21

²( R 1 r )

xe2Ah      sin h I

+T3 - z (T3 - T4).(4)

h

дукта; vr ,vz - проекции скорости точек продукта на оси r ; z, a – коэффициент темпера- туропроводности;

v^ 1 5p r   p д r

= v

( д ² v    1 8 v    8 ² v

----r _ + c + r _v д r ² r д r д z ²

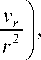
где p - давление в точках продукта; v - коэффициент кинематической вязкости продукта;

r = R ,r = R 2 ,P = Pi, p = P2 ,t = T, T = Ti,    ,         (3)

T = T ₃ , z = 0 , z = h, v r (r, 0 ) = 0 ,f ( 0 ) = 0

где Р 1 – модифицированное давление на входе продукта в междисковое пространство; Р 2 – модифицированное давление на выходе продукта; h – расстояние между дисками; T ₃ и T ₄ - температура продукта на стенках дисков.

Однако каждый теплообменный элемент должен рассчитываться, исходя из своих граничных условий (температура на входе и температуры охлаждающих стенок). По этой причине непосредственное применение выражения (4) для практических расчетов малопригодно, так как нужно знать температуру продукта на входе в каждый элемент и температуру стенок дисков в этом элементе. В силу этого расчет теплообменного элемента будет состоять из двух основных этапов: 1 этап – определение температуры стенок каждого элемента охладителя и 2 этап – определение температуры продукта на выходе из охладителя.

Температура стенок охладительного элемента, или температура хладагента, не может быть рассчитана аналитически ввиду сложности канала, по которому течет хладагент. Поэтому найдем ее приближенно, считая, что она одинакова на всех стенках данного элемента. Для этого используем формулу, аналогичную формуле В.Г. Шухова, примени- мую для расчета температуры жидкости, те-

кущей в круглой прямой трубе с нагретыми

стенками [2]:

Т _ Тц+ T

Txi =    2    +

T x , I 1

V

- T) e "в h, (5)

2 J

Txо ±А =

_ T 11 + ^T 21 .U T 11 + T 21 V

= 2 + V T ⁰      2 J e ,

где _p = 2 SK ,                           (6)

cp pqx l - средняя длина канала для хладагента в каждом элементе; S - средняя площадь сече

в котором температура продукта T ₂₁ на выходе из первого элемента рассчитывается по

формуле

при

r = R2,

ния канала для хладагента в каждом элементе; K - коэффициент теплопередачи через стенку между хладагентом и продуктом; р - плот

T 3 = T 4 = T x 1 = T x о ±А , функций, зависящих от между дисками.

Из (7) находим

—

T 1 = T 11 и осреднении z по толщине зазора

ность хладагента; c p - теплоемкость хладагента при постоянном давлении; T и T ₂ i - соответственно температура продукта на входе в элемент с номером i и температура продукта на выходе из этого элемента; T . , - темпера- X , i 1

тура хладагента на входе в i -й элемент;

1 i + ² i - средняя температура продукта в 2

в L = 1П 1 ± h

V

2 А зт -Т

² T x о T 11

—

Т

T 21

Hа вид

основании (8)

формула (5) примет

T xi

^T 1 i + ^T 2 i

2 T x 0

+ 1 T_

2 А

—

T

—

^T 1 i + ^T 2 i

— I

x

^T 21 j

каждом элементе; q x - расход хладагента.

Коэффициент в не может быть рассчитан по формуле (6), поскольку для каналов сложной формы коэффициент теплопередачи K может быть определен только экспериментально. Поэтому определим весь комплекс — el, входящий множителем в показатель h экспоненты (5), задавшись температурой хладагента в каком-либо элементе. Проще всего это сделать для первого элемента i = 1. При этом учтем, что течение хладагента может быть как в сторону течения продукта (прямоток), так и противоположно этому течению (противоток). Тогда для первого элемента можно записать

Tx I = Tx о ±А, где Tx । - средняя температура хладагента в первом элементе; Tx0 - температура хладагента на входе в первый элемент (при прямотоке) или на выходе из первого элемента (при противотоке), А - разность температур хладагента в первом элементе и на входе (выходе) из него, которую можно найти экспериментально. Знак плюс соответствует случаю прямотока, а знак минус - случаю противотока. Тогда из (5) получим уравнение для определения комплекса в 1 —

h

Таким образом, по формуле (9) можно приближенно найти температуру стенок для элементов i = 1,2,... N .

Преобразуем теперь формулу (4) так, чтобы с ее помощью можно было бы найти температуру продукта на выходе из любого охлаждающего элемента. Для этого положим, что температура всех стенок данного элемента с номером i примерно одинакова и определяется по формуле (9). Тогда в (4) следует положить T₃ = T ₄ = T_xi , T 1 = T 1 i , а истинную температуру в каждой точке охлаждающего элемента заменить средней температурой по толщине зазора между дисками при радиусе r = R ₂, т. е. T ( r , z ) * T ₂ i , где T и T 2 . - температура продукта на входе в элемент с номером i и температура продукта на выходе из этого элемента. После этого преобразованная формула примет следующий вид:

T, = —г г f l к Г ( T , — T ,)( 1 — ^cos k n ) 1Г R ² — R ² — k- ^ T ( R ⁴ — R 4 ) — T A-h - lx ² ‘ A ² h ² Й[ ^{L( 1} ‘ ^x‘ ^{)(              11 2      1} 2 Ah ^{2 2      1} к ² n ² J

x

l 2-2                                 1

^{к П} - Р²_Р ²l ,            , I

, 2 Ah 2( R¹ R ^{2 )} 1 — COS к п I

+ T .

xi кп I

По формуле (10) последовательно подсчитывается температура на выходе из любого охлаждающего элемента, начиная с первого по ходу течения продукта. Подсчет прекращается для такого количества теплообменных элементов i = N, при котором температура продукта на выходе из этого элемента станет равной заданной конечной температуре T2N. Следует иметь в виду, что температура про-

дукта на выходе из любого элемента T _{2 i} присутствует как в равенстве (9), так и в равенстве (10). Поэтому ее определение будет связано с решением системы уравнений (9) и (10). В равенство (10) вместо T _xi подставляется правая часть (9) и решается уравнение относительно T _{2 i} , при этом температура _T на входе в элемент с номером i равна температуре продукта на выходе из предыдущего i - 1 элемента.

Пример расчета. Определить количество теплообменных элементов для охладителя сгущенного молока для следующих исходных данных: температура продукта на входе – T 1 = 80 ° C , температура продукта на выходе - T ₂N = 16 ° C , температура хладагента на входе в первый элемент (при прямотоке) или на выходе из первого элемента (при противотоке) – T x ₀ = 2 ° C , радиус входного отверстия - R 1 = 0,041 , радиус, на котором расположены выходные отверстия - R ₂ = 0,21 , расстояние между пластинами - h = 0,0151 , коэффициент температуропроводности продукта – a = 10 ^{- 7}1 ²/с, расход продукта - q = 4 • 10 ^{- 4}1 ³ / с, разность температур хладагента на входе и выходе в первом элементе – А = 0,8 o N .

Пример расчета приведен для движения продукта и хладоносителя по схеме прямотока и противотока.Все численные расчеты количества теплообменных элементов проведены в прикладном вычислительном пакете MATHCAD.

Прямоток. Из расчета следует, что заданная температура продукта t ₂ N = 16 o C примерно достигается при количестве теплообменных элементов i = N = 20 шт и составляет 15, 9 °С. Зависимость температуры продукта на выходе из последовательно установленных теплообменных элементов при прямоточной схеме течения сред показана на рис. 3. При этом температура хладоносителя на выходе из аппарата равна T x ₂₀ = 8,4 ° C.

Для противоточной схемы течения сред (рис. 4) задаем температуру хладоносителя T x ₀ = 12 ° C и разность температур А = 1 ° C .

Зависимость температуры продукта на выходе из последовательно установленных теплообменных элементов при противоточной схеме течения сред показана на рис. 4. При этом температура хладоносителя на выходе из аппарата равна T x ₂₀ = 2,3 ° C.

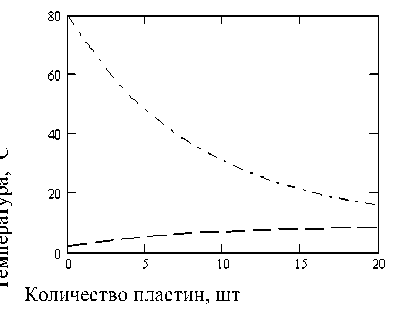
Рис. 3. Зависимость температуры продукта от количества теплообменных элементов при прямоточной схеме течения сред: T_xi - температура хладагента ʙ i ‒м элементе, Т _{2 i} - выходная температура продукта из i – го элемента; i – количество охладительных элементов

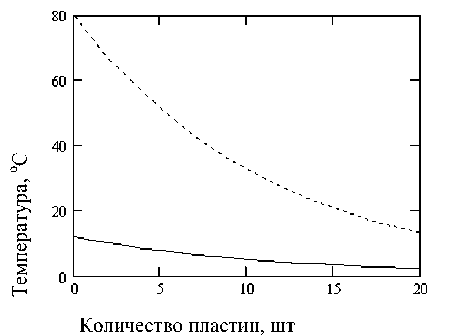
Рис. 4. Температурный график скребкового теплообменного аппарата при противоточной схеме течения сред

Из расчета следует, что заданная температура продукта T _{2 N} = 16 ° C примерно достигается при количестве теплообменных элементов i = N = 20 шти составляет 15, 9 °С.

Разработанная методика расчета пластинчатого скребкового теплообменного аппарата позволяет определять количество теплообменных элементов в зависимости от температурных режимов в аппарате.