Разработка методик обработки сигналов плавления ДНК

ВВЕДЕНИЕ                 УСЛОВИЯ И ПАРАМЕТРЫ РЕАЛИЗАЦИИ

МЕТОДА ПЛАВЛЕНИЯ ДНК

Метод плавления ДНК основан на эффекте перехода двойной спирали молекулы ДНК в клубкообразное состояние при повышении температуры. При этом наблюдается резкое изменение интенсивности сигналов флуоресценции красителей, присоединенных к молекуле ДНК [1, 2].

В качестве температуры плавления ДНК ( T m ) обычно принимается положение на температурной оси максимума первой производной сигналов плавления. Значение T m зависит от длины фрагмента ДНК и процентного содержания суммы нуклеотидов C и G [2–6].

Для выполнения операции плавления ДНК необходимо выбрать пределы изменения температуры, шаг изменения температуры (от 0.1 до 1 ºС) и время наблюдения флуоресценции при каждом шаге (20 с и более). Эти величины определяют трудоемкость (длительность) эксперимента, а также отношение сигнала к шуму. Все эти параметры влияют на погрешность измерения величины T m .

В настоящей статье для формулировки адекватной задаче методики обработки сигналов плавления ДНК (СП) использованы и сравниваются аппроксимационные усовершенствованные модели СП на базе нелинейной сигмоидальной функции (СФ) и ее производной [7, 8], модель на основе функции Гаусса (ФГ) и модели на основе сте-пенн х полиномов. Определены особенности этих моделей и выполнено сравнение результатов их применения. В работе использованы вычислительные средства пакета MATLAB.

Влияние шумов, дрейфа нулевой линии и дискретизации сигналов может быть в значительной степени уменьшено путем обработки сигналов с помощью аппроксимирующей функции.

Можно принять в качестве критериев успешности методики обработки СП величину погрешности измерения T m , длительность эксперимента, количество параметров и критичность выбора параметров аппроксимирующей функции.

Исходные (сырые) данные кривой плавления ДНК получены на анализаторе нуклеиновых кислот АНК-32, который серийно выпускается в Институте аналитического приборостроения РАН (ИАП РАН). В качестве образца был использован комплекс зонд—ДНК—мишень с флуорофором (ROX) в комбинации с гасителем производства ЗАО "СИНТОЛ" [9].

Для обеспечения погрешности T m порядка 0.1 ºС выбраны следующие условия: диапазон температуры 82–90 ºС, шаг изменения температуры 0.2 ºС, время наблюдения при каждом шаге 60 с (общее время анализа примерно 50 мин).

РЕЗУЛЬТАТЫ РЕАЛИЗАЦИИ МЕТОДИКИ ОБРАБОТКИ СП НА ОСНОВЕ

УСОВЕРШЕНСТВОВАННОЙ СФ-МОДЕЛИ

Усовершенствованную модель кривой плавления на базе СФ предлагается выразить для использования в программе MATLAB в виде формулы

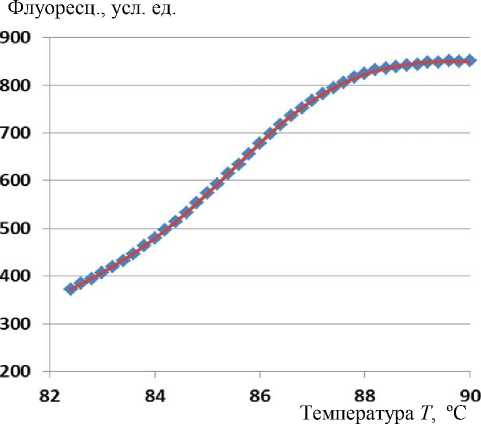
Рис. 1. График кривой плавления ДНК одной из проб (1) и график модельной СФ (2)

Характеристики СП, вычисленные по разным методикам для 8 последовательно расположенных проб

№ пробы	Точки T m, вычисленные по методикам обработки СП						Уточнение данных для методики Полином-7
	СФ	Произв. СФ	Гаусс	Гаусс М	Полином-3	Полином-7
							Т mt	T md
	Д. 1	Д. 2	Д. 3	Д. 4	Д. 5	Д. 6
В1 В2 В3 В4 В5 В6 В7 В8	85.54 85.50 85.49 85.49 85.56 85.58 85.68 85.84	85.52 85.52 85.48 85.49 85.57 85.61 85.75 85.93	85.70 85.66 85.67 85.65 85.73 85.75 85.842 86.00	85.5 85.46 85.46 85.45 85.53 85.55 85.65 85.81	84.99 84.95 84.93 84.96 85.06 85.08 85.21 85.45	85.52 85.51 85.46 85.48 85.59 85.58 85.68 85.89	85.53 85.49 85.47 85.49 85.54 85.61 85.72 85.86	–0.01 0.02 –0.01 –0.01 0.06 –0.03 –0.04 0.03
Стандартные отклонения
d T mсо d T ms	0.12 0.03	0.16 0.02	0.12 0.02	0.12 0.02	0.18 0.03	0.14 0.03	— —	— 0.03

f = @(x,u)  (x(2)./(1+exp((x(1)-

-u) ./x(3)))) + x(6)*u.A2 +

+ x(5)*u + x(4) ,               (1)

где f — относительная величина интенсивности флуоресценции при температуре образца u (°C);

x(1) — значение температуры плавления T m (°C) с шагом 0.1 (°C);

x(2) — относительная интенсивность (размах) участка плавления;

x(3) — коэффициент, который определяется наклоном кривой;

x(4) , x(5) , x(6) — коэффициенты, учитывающие смещение, а также линейную и квадратичную зависимости нулевой линии от температуры.

Результаты обработки СП по различным рассматриваемым в статье аппроксимационным методикам для 8 проб сведены в таблице. Столбцам данных для краткого их обозначения присвоены номера Д. 1–6.

Значения вычисленных T m по методике "Аппроксимация СФ" приведены в столбце СФ (Д. 1).

На рис. 1 приведен график кривой плавления ДНК одной из проб. На него наложен график модельной СФ с оптимизированными параметрами.

Можно отметить хорошее совпадение этих графиков.

РЕЗУЛЬТАТЫ РЕАЛИЗАЦИЯ МЕТОДИКИ ОБРАБОТКИ СП НА ОСНОВЕ УСОВЕРШЕНСТВОВАННОЙ МОДЕЛИ ПРОИЗВОДНОЙ СФ

Можно отметить некоторые особенности дифференцирования СП.

Дифференцирование предложено выполнять по формуле (2):

V ( j ) = ( s ( j + 2) – s ( j )) / 2,              (2)

где V ( j ) — результат дифференцирования на j- м шаге; s ( j + 2) и s ( j ) — исходные данные для ( j + 2) и ( j ) шагов соответственно.

В результате дифференцирования значительно ухудшается отношение сигнала к шуму, что можно объяснить следующими причинами. В результате вычитания двух сигналов, обладающих шумовыми составляющими в виде случайных величин, шум увеличивается в 1.41 раза.

Максимальное значение дифференцированного сигнала пропорционально шагу изменения температуры. В качестве сигнала сырых данных можно принять размах СФ. Этот сигнал содержит N шагов изменения температуры. При дифференцировании выполняется вычитание сигналов сырых данных, отличающихся на 1 шаг, поэтому сигнал ориентировочно уменьшается в N раз.

Улучшить отношение сигнала к шуму можно путем увеличения времени наблюдения при каждом шаге, но это приводит к значительному увеличению длительности эксперимента.

Результаты обработки СП на основе производной СФ приведены в столбце Д. 2 таблицы. На рис. 2 приведены график производной кривой плавления ДНК одной из проб и график производной СФ. Можно отметить эффективное сглаживание шума и компенсацию дрейфа нулевой линии за счет применения аппроксимирующей кривой.

МЕТОДИКА ПОСТРОЕНИЯ УСОВЕРШЕНСТВОВАННОЙ МОДЕЛИ И ОПТИМИЗАЦИИ ПАРАМЕТРОВ ПРОИЗВОДНОЙ КРИВОЙ ПЛАВЛЕНИЯ НА ОСНОВЕ ФУНКЦИИ ГАУССА

Усовершенствованная модель производной кривой плавления на базе функции Гаусса использована в программе MATLAB в виде формулы (3): f =

= @(x,u) x(2)./(1.77245.*x(3) ).*exp(--(u-x(1) ).A2./(2.*x(3).A2) )+x(4) +

+ x(5)*u ,                                (3)

где f — относительная величина интенсивности флуоресценции при температуре образца u (°C);

x(1) — значение температуры (математическое ожидание), соответствующее максимальному значению функции Гаусса (°C);

x(2) — максимальное значение функции Гаусса;

x(3) — полуширина функции приблизительно для уровня 0.6 от максимального значения функции.

Для учета смещения и линейной зависимости нулевой линии от температуры в усовершенствованную модель предложено ввести слагаемые x(4) + x(5) *u .

Начальные значения параметров можно вычислить путем обработки данных производной кривой

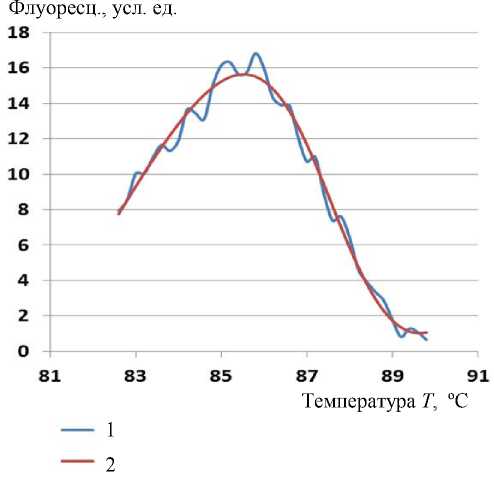
Рис. 2. График производной кривой плавления ДНК одной из проб (1) и график производной СФ (2)

Флуоресц., усл. ед.

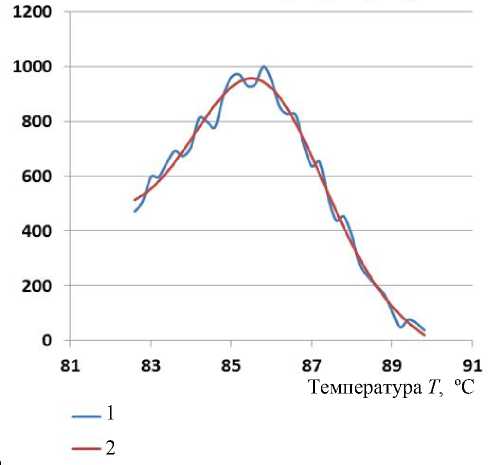
Рис. 3. График производной кривой плавления ДНК одной из проб (1) и график усовершенствованной модели на базе ФГ (2)

плавления. По графику "на глаз" находится максимальное значение x(2) и соответствующее этому значению величина x(1) .

Уточнить начальные параметры можно путем аппроксимации данных производной кривой плавления функцией Гаусса без слагаемых x(4) и x(5)* u .

Команды программы MATLAB сохраняются в виде M-файла, при этом расчет температуры плавления может выполняться в автоматическом режиме.

Можно отметить некоторые особенности приведенной формулы. Значение x(1) относится к симметричной функции Гаусса. Можно использовать значение x(1) в качестве температуры плавления T _m. Эти результаты обработки СП приведены в столбце Гаусс (Д. 3) таблицы.

Однако если использовать определение T m как максимальное значение кривой плавления, то можно добавить операцию нахождения этого максимального значения по формулам (4)–(7):

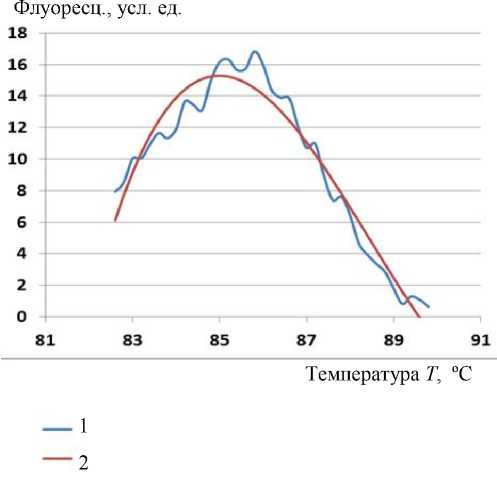
Рис. 4. График производной СП (1) и график аппроксимации полиномом 3-й степени (2)

s = (t(1):0.01:t(m)),(4)

Vnn = f(xx,s),(5)

[pks, locs] =

= findpeaks(Vnn,'minpeakdistance',15) , (6)

an = s(locs),(7)

где

Vnn — значение модельной функции в диапазоне s с шагом 0.01 (°C);

an — значение T m как результат нахождения максимального значения этой функции.

Результаты обработки производной СП приведены в столбце Гаусс М (Д. 4) таблицы.

График усовершенствованной модели на базе функции Гаусса одной из проб (рис. 3) практически аналогичен графику производной СФ на рис. 2.

МЕТОДИКА ПОСТРОЕНИЯ УСОВЕРШЕНСТВОВАННОЙ МОДЕЛИ И ОПТИМИЗАЦИИ ПАРАМЕТРОВ ПРОИЗВОДНОЙ КРИВОЙ ПЛАВЛЕНИЯ

НА ОСНОВЕ СТЕПЕНН Х ПОЛИНОМОВ

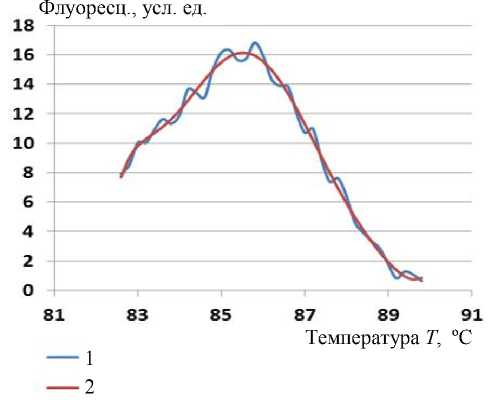
Рис. 5. График производной СП (1) и график аппроксимации полиномом 7-й степени (2)

Модель производной кривой плавления на базе полиномов предлагается выразить для использования в программе MATLAB в виде формулы (8):

koaf=polyfit(t,V, n) ,            (8)

где V — значения производной СП при температуре t ;

n — значения степени полинома (в приведенных примерах n = 3 или 7).

Результаты обработки производной СП на основе усовершенствованной модели на базе полиномов приведены в столбцах данных Д. 5 и Д. 6 таблицы.

Аппроксимация полиномом 3-й степени имеет существенный недостаток: ее график (рис. 4) значительно сдвинут относительно графика производной СП.

График аппроксимации полиномом 7-й степени (рис. 5) практически аналогичен графику произ- водной СФ (рис. 2) и модели на базе функции Гаусса (рис. 3).

ОЦЕНКА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ ДНК

ПРИ ИСПОЛЬЗОВАНИИ ПРЕДЛОЖЕННЫХ МЕТОДИК ОБРАБОТКИ СИГНАЛОВ ПЛАВЛЕНИЯ И ИХ ПРОИЗВОДНЫХ

Результаты определения температуры плавления T m приведены в таблице. Эти же результаты приведены в виде графиков зависимостей от номера пробирки с пробой на рис. 6 (номера пробирок и проб одинаковы). Для наглядности точки графиков соединены прямыми линиями. На графиках величины T m (вертикальная ось, ºС) зависят от номера пробирки (горизонтальная ось, числа 1–8 определяют место последовательного расположения в держателе пробирок) и от методик обработки СП.

При сравнении графиков на рис. 6 можно отметить следующие особенности: кривые Гаусс М (Д. 4) и Полином-7 (Д. 6) почти полностью совпадают.

Зависимость величины T m от номера пробы можно объяснить неравномерностью температурного поля прибора (систематическая погрешность измерения). Отклонение от этой зависимости можно считать случайной погрешностью.

Для количественной оценки полной погрешности определения температуры плавления ДНК вычислены в среде Excel значения стандартного отклонения в каждом столбце Д. 1–6 таблицы по формуле (9):

dT mсо = СТАНДОТКЛОН(Х1:Х8) , (9)

где Х1:Х8 — значения в 8 ячейках для В1–8 соответствующих столбцов.

СПОСОБ ОПРЕДЕЛЕНИЯ НЕРАВНОМЕРНОСТИ ТЕМПЕРАТУРЫ ПРОБИРОК

Неравномерность температуры пробирок анализатора нуклеиновых кислот можно считать систематической погрешностью определения значения T m .

Можно отметить нелинейность зависимости значения T m от номера пробирки. Пробирки с номерами 1 и 8 расположены вблизи противоположных краев держателя пробирок. Их значения T _m больше, чем у пробирок, расположенных ближе к центру держателя пробирок (так называемый "краевой эффект").

Поэтому для выделения систематической погрешности для каждой модели построена полиномиальная (со степенью 2) линия тренда и определены 3 коэффициента уравнения аппроксимации. Согласно этому уравнению, найдены уточненные табличные значения Т mt . В качестве примера графики для методики Полином-7 приведены на рис. 7.

Для примера в таблице для методики Полином-7 приведены значения Т mt и T md = T m – Т mt . Затем по формуле (9) вычислены значения стандартного отклонения d T ms для методики Полином-7 и др.

Т о/-, m,

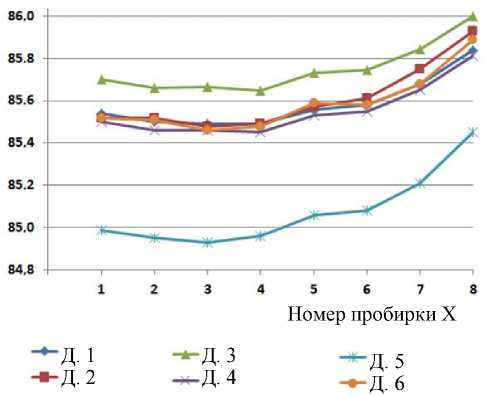
Рис. 6. Зависимости T m от номера пробирки X = 1–8 по данным таблицы для различных методов

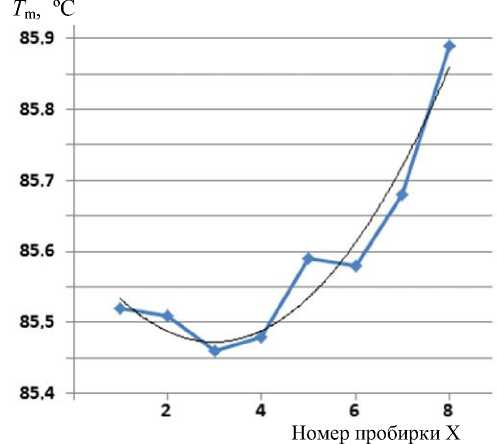
Рис. 7. Зависимость значения T m от номера пробирки для методики Полином-7 (ломаная линия) и полиномиальная (со степенью 2) линия тренда y = 0.0154 x ² – 0.0922 x + 85.611

Поскольку величины d T ms для всех методик находятся в пределах 0.02–0.03 ºС, то можно сделать вывод о том, что все методики обеспечивают приблизительно равные случайные погрешности. Однако модель на основе полиномов 7-й степени позволяет стандартными средствами MATLAB полностью автоматизировать вычисления без предварительного выбора параметров.

ЗАКЛЮЧЕНИЕ

• 1.    Выбраны условия и параметры реализации методики плавления ДНК.

• 2.    Разработаны методики обработки сигналов плавления ДНК, в которых использованы следующие усовершенствованные модели: модель на базе нелинейной сигмоидальной функции; модель на основе производной от сигмоидальной функции; модель на основе функции Гаусса и модель на основе степенн х полиномов.

• 3.    Показана возможность автоматизации вычислений при использовании программы MATLAB. Отмечено преимущество методики с применением усовершенствованной модели на основе степенн х полиномов, полностью автоматизирующей вычисления стандартными средствами MATLAB без предварительного выбора параметров.

• 4.    Показана возможность разделения систематической и случайной погрешностей определения температуры плавления ДНК.

• 5.    Предложен способ определения неравномерности температуры пробирок.