Разработка методики оптимизации параметров штампов компрессорных лопаток авиационных двигателей
Автор: Хаймович Ирина Николаевна
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Научная жизнь
Статья в выпуске: 4-1 т.16, 2014 года.
Бесплатный доступ
В статье разработана методика определения оптимальных параметров обжимных и обрезных штампов компрессорных лопаток авиационных двигателей на основе математической модели с целевой функцией, минимизирующей сдвигающие усилия на поверхности замка, пера и мостика объектов заготовительно-штамповочного производства. К параметрам оптимизации относятся оптимальный угол поворота поковки в штампе, угол поворота и ширина облойного мостика. Использование данных оптимальных параметров при проектировании штампов позволит повысить точность размеров поковки, повысит стойкость штампа, снизит расход металла на штамповочные уклоны.
Обрезные и обжимные штампы, компрессорные лопатки, сдвигающие усилия, математические модели штамповой оснастки, алгоритм оптимизации, угол поворота поковки в штампе
Короткий адрес: https://sciup.org/148203172
IDR: 148203172 | УДК: 004:33
Текст научной статьи Разработка методики оптимизации параметров штампов компрессорных лопаток авиационных двигателей
пряжений в области пера Px (рис. 2), в области формирования хвостовика (Qx) и в области мостика заусеничной канавки вдоль подошвы хвостовика (Gх) (рис.5), стремящихся сместить вкладыши штампов.
Суммарные сдвигающие усилия при известной геометрии поковки, в основном, определяются величиной угла ТАУ3. Правильно выбранный поворот поковки в штампе позволяет:
-
1. Уменьшить сдвигающие горизонтальные усилия на обе половины штампа, повысив за счет этого точность размеров поковки.
-
2. Облегчить заполнение гравюры штампа и повысить его стойкость.
-
3. Создать условия для надежной укладки заготовки в штамп перед ее деформацией.
-
4. Создать базы контроля размеров поковки на торце хвостовика и снизить расход металла на штамповочные уклоны.
Этот угол может быть принят в качестве одного из независимых варьируемых параметров при постановке задачи оптимизации. На величину сдвигающих усилий также влияют: размеры мостика заусеничной канавки (b/MOST) (рис. 4) и угол его поворота jj относительно оси штампа (рис. 5). Для определения оптимальных параметров штамповой оснастки применим метод математического моделирования [1, 3, 5-7], а затем, используя рассчитанные параметры, можно автоматизировать и построение объектов заготовительно-штамповочного производства в среде CAD – системы [2, 4].
Целевая функция имеет вид:
А + В + С ^ min , (1) где А – сдвигающие усилия на поверхности пера,
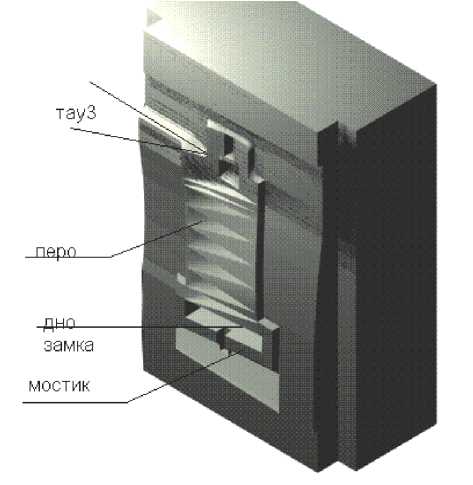
Рис. 1. Угол поворота поковки в штампе на нижнем вкладыше
В – сдвигающие усилия на участке замка,
С – усилия, действующие на поверхность мостика.
Для решения поставленной задачи необходимо знать закон распределения нормальных напряжений на каждом участке гравюры штампа. Деформацию металла на участке формирования пера можно с достаточной точностью рассматривать как осадку широкой полосы под плоскими плитами, если принять следующие допущения:
-
1. Кривизна профиля поперечного сечения гравюры пера в каждом сечении меняется незначительно и не влияет на величину и характер распределения нормальных напряжений.
-
2. Толщина деформируемого пера постоянна и равна среднему значению в пределах каждого сечения.
С учетом указанных допущений можно принять линейный закон распределения нормальных напряжений (рис. 3) в виде:
Р = ст s * (1+(0.5a-x) / h), (2) где а – ширина профиля гравюры пера в каждом сечении по хорде; h – средняя толщина полосы в каждом сечении.
h = Fсеч/ а, (3) где Fсеч – площадь поперечного сечения профиля пера поковки в рассматриваемом сечении.
_ * 2 _CTs " Vs CTs , (4)
где CT s — предел текучести штампуемого материала.
Эпюра нормальных напряжений на участке мостика может быть описана уравнением :
G = ст s * (1 + b / MOST). (5)
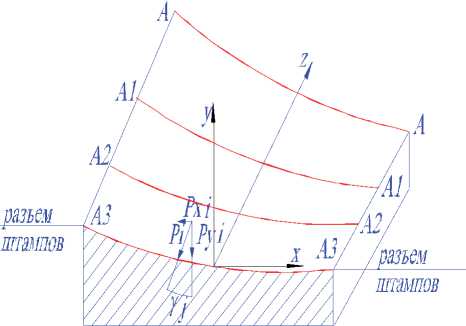
Рис. 2. Схема разложения вектора нормальных напряжений на участке гравюры пера
(А-А, А1-А1, А2-А2, А3–А3 – сечения пера штампа)
В этом выражении отношение b / MOST является переменной величиной и задается из технологических соображений в пределах: 4 < b / MOST < 6. На рис. 4 показана эпюра распределения нормальных напряжений вдоль оси гравюры штампа. Анализ эпюры показывает, что характер изменения напряжений в области хвостовика определяется по сложному закону в зависимости от стадии заполнения полости штампа. В конце процесса в этой области напряжения могут достигать максимального значения. В целях упрощения задачи приняты средние значения напряжений в этой области:
Q = ( ст * (1 + ——) + ст * (1 + °'5 a " x )) /2 , (6)
ср s MOST s h
Для нахождения сдвигающего усилия в области пера вся поверхность пера разбивается на конечные участки (рис. 2). Усилия, приходящиеся на единицу поверхности, находятся из разложения нормальных напряжений. Ввиду незначи-
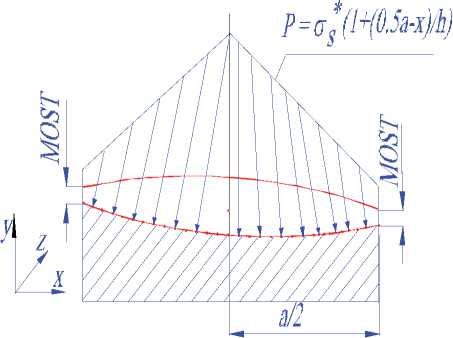
Рис. 3. Эпюра распределения нормальных напряжений по ширине гравюры пера
* , X X
P= о s (1+(0.5a-x)/hmax)
G o s (1+b/MOST)
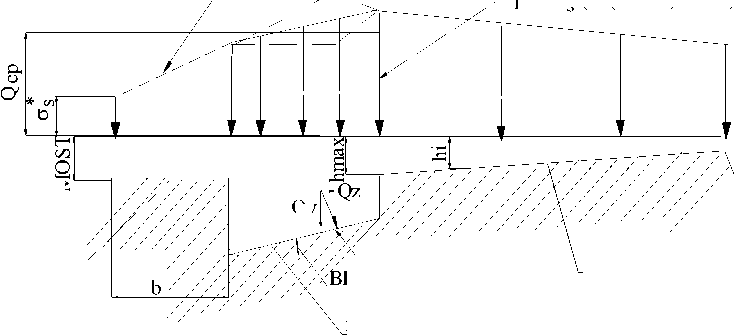
Qy мостик перо хвостовик
Fз ETA1/2
Рис. 4. Эпюра распределения нормальных напряжений вдоль оси гравюры штампа
тельного уклона гравюры штампа в направлении оси OZ составляющей Pzi пренебрегаем. Тогда
Pxi = P yi tg Y i , (7)
где Pxi , Pyi – составляющие вектора нормальных напряжений.
Общее сдвигающие горизонтальное усилие можно получить из выражения:
A = Л P xi dF .
F
где Pxi – горизонтальное усилие, действующие на единицу площади гравюры пера.
Так как перо разбивается на конечные участки, то для нахождения усилия на всей поверхности пера перейдем от интеграла к сумме:
n 1 n 2
A = EE P ( j tgV y , (9)
i = 1 j = 1
где P ( x ij ) – эпюра нормальных напряжений на поверхности пера;
Y j - угол наклона касательной к оси ОХ в средней точке участка поверхности.
После подстановки получаем:
л! nl 0 5 a - x
A = E w* E (1 + ") tg ( Y j + TAY 3) ,(11)
i=1 j=1 hi где Yj + TAY 3 определяет новое положение касательной.
Теперь выражение А полностью определяет сдвигающие усилия по всей поверхности пера штампа.
На гравюру штампа в области хвостовика действуют напряжения Qср. Разложение Qср по трем осям принимает вид:
Q y = Q cp cos( BETA1/2) , (12)
Q x = Q y sin TAY 3 = Qcp cos( BETA1/2)sin TAY 3, (13) где ВЕТА1 – угол наклона поверхности хвостовика вдоль оси OZ (рис. 4), а Qср –величина средних напряжений в продольном сечении штампа.
Cдвигающее усилие, действующее на участке замка, находится по формуле:
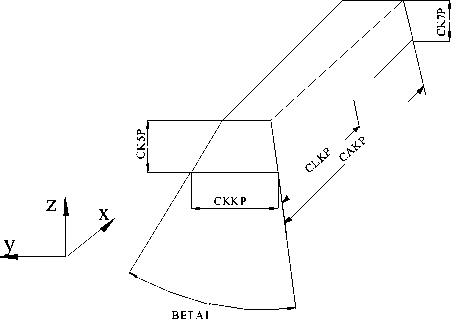
В = ff Q x dFз , (14)
Fз где границы площади замка Fз изменяются в пределах -clkp n1 n2 а = EE ^(1+ I=1 j=1 0,5 ai - xy hi )tgYj , (10) В = ^2^ cos( BETA1/2)sin TAY 3 cakp (ck 5 p + ck 7 p )/2 x где n1– количество разбиений по оси z, n2 – количество разбиений по оси х, l – длина пера между разбиениями по z, a – хорда сечения пера по х. Угол поворота поковки в штампе естественно изменяет положение любого элемента поверхности.. Тогда выражение (10) примет вид: b 0.5a 1 x (2 +--+----(cakp - 2clkp)) MOST h h ,(15) где ck5p, ck7p, cakp, clkp – габаритные размеры хвостовика (рис. 6). На мостик действуют нормальные напряжения G. В виду того, что гравюра хвостовика повернута в штампе на ТАУ3, угол наклона мостика ф = ( ф 1 + ТАУ3) будет определять величину Рис. 5. Расчет угла наклона мостика ф к оси штампа сдвигающего горизонтального напряжения: Gx = G sin ф . (16) Общее усилие, действующее на площадь мостика: С = JJG sin фdFм. Fм Границы площади мостика находится в пределах 0 G ^ (1 +-------) . s MOST. После интегрирования имеем: С = <г*(1 + MosTbsin(ф1 + TAY3)cakp/cosф1. (19) Таким образом, значение функции цели связано с назначенными варьируемыми параметрами (формулы 1-19). Установим систему ограничений. Все ограничения являются параметрическими. Угол TAY3 теоретически может меняться в пределах –90 до 90 градусов. На параметр b/ MOST накладываются технологические ограничения от (b/MOST)min до (b/MOST)max . Разъем штампов по подошве хвостовика лопатки может переходить из области (а2-а1) по входной кромке в область (с2-с1) – по выходной. Угол мостика заусеничной канавки может изменяться в пределах от - ф 1 до ф 1max (рис.5), где ф 1 задаются из конструктивных соображений, т.е. ■ с1 - c2 , , ■ c2 - al arcsin-------< ф1 < arcsin-------. (20) cakp cakp Тогда система ограничений для принятой целевой функции (1) сформирована из геометрических и технологических соображений имеет следующий вид: Рис. 6. Габаритные размеры хвостовика Таблица 1. Результаты использования предлагаемого алгоритма оптимизации для заготовок компрессорных лопаток двигателя НК-36 № изделия b/h ф1, град. TAY3, град. Целевая функция 1 5.14 2.67 -8.20 0.07 2 5.99 0.53 -5.34 0.02 3 5.20 5.85 -7.98 0.09 Q = ^ 4 < —-— < 6 MOST ■ cl - a 2 ■ c 2 - al arcsin-------< ф1< arcsin-------. (21) cakp cakp - 90 < TAY3 < 90 Итак, в качестве вектора варьируемых параметров выбираем х= {TAY3, b/MOST, ф}, система ограничений - Q , функция цели - величина сдвигающего усилия. Сформулируем задачу минимизации сдвигающих усилий в терминах математического программирования. Найти вектор х*, принадлежащий области Q = {х: хmin< x < xmax}, такой, чтобы F(x*) было минимальным для любого х из области Q . Целевая функция (1) выпуклая и ограничения тоже выпуклые. Это позволяет решать задачу с помощью эффективного метода деформируемого многогранника (комплексный метод Бокса). Он является модификацией симплексного метода Нелдера – Мида, однако позволяет учитывать наложенные ограничения. Решаемая задача состоит в минимизации функции вида: f(x)=f(x1,x2,^,xn), где х1= TAY3, x2 = ф 1, x3=b/ MOST, и значения х задаются с помощью явных ограничений lj < xj < uj, j=1,^,n. (22) Значения lj и uj являются нижней и верхней границами переменных. В нем предполагается, что известны значения n, ljи uj и начальная точка х1, удовлетворяющая всем ограничениям (22). В первую очередь необходимо выбрать k точек, которые удовлетворяют ограничениям, а также вычислить целевую функцию во всех k точках. Множество этих точек есть комплекс, k=2n. Точка х1, удовлетворяющая всем ограничениям, задана ( ф 1 = 0.0, ТАУ3=0.0, b/h = 4.0) . Остальные точки, удовлетворяющие неравенству (22), могут быть выбраны следующим образом: xij = lj+r (uj - lj),j=1,…,n; i=2,…,k, (23) где r – псевдослучайная равномерно распределенная переменная в интервале (0,1). Точки, выбираемые в соответствии с уравнением (23) для данного j, будут автоматически удовлетворять неравенству (22). Конечно, поскольку точка х1 находится внутри области ограничений, то комплекс будет состоять из допустимых точек. При нахождении точки минимума вычисляются две величины, использующиеся при проверке сходимости метода: среднее квадратичное отклонение о для k значений функции и максимальное расстояние dm между двумя точками комплекса. Первая величина вычисляется через ss2: о ' (Xe )2 - 'f1 e=1 k Величины о2 и dm проверяются на сходимость к заданной точности Е 1= 0.01, Е2 = 0.001 и процедура поиска минимума заканчивается. Пользуясь разработанным методом оптимизации для вектора варьируемых параметров (b, ф 1, TAY3), были получены результаты (табл. 1) для трех заготовок компрессорных лопаток: оптимальный угол поворота поковки в штампе, угол поворота и ширина облойного мостика на торце хвостовика. Полученные параметры позволяют сформировать поверхность разъема штампа в области хвостовика, оптимизировать угол поворота поковки в штампе, обеспечив практически полное отсутствие сдвигающих горизонтальных усилий на вкладыши штампов. Численная величина па- раметров не противоречит аналогичным значениям, применяемым на производстве для отлаженных технологических процессов.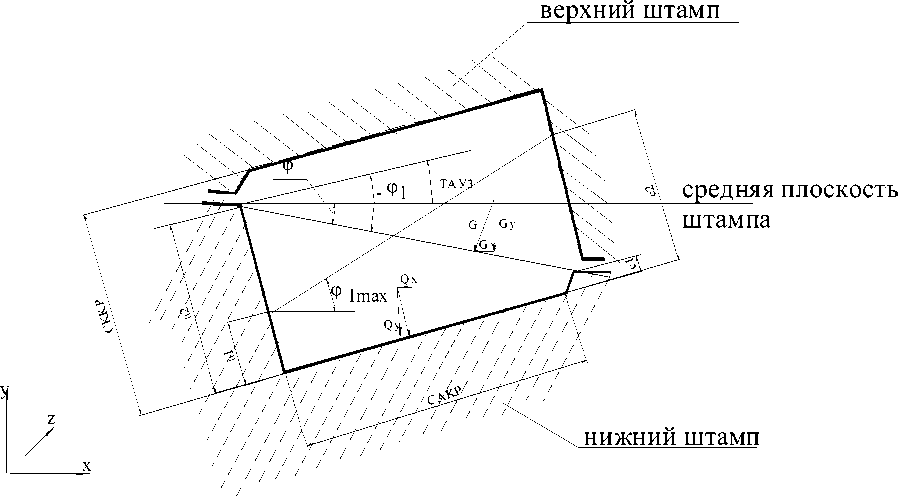
Список литературы Разработка методики оптимизации параметров штампов компрессорных лопаток авиационных двигателей
- Хаймович И.Н., Клентак Л.С. Усовершенствование методов сглаживания сложных поверхностей с использованием интерполяционных сплайнов//Фундаментальные исследования. 2013. №10 (часть 12). С.1228-1232.
- Попов И.П., Маслов В.Д., Севериненко А.Ю. Применение CAD/CAE -систем в исследовании процессов формообразования тонкостенных тройников//САПР и графика. 2012. №1. С.86-88.
- Оводенко А.М., Арышенский Е.В., Гречникова А.Ф., Беглов Э.Д. Разработка математической модели распределения сил натяжения по ширине полосы при горячей прокатке в непрерывной группе стана//Известия Самарского научного центра РАН. 2011. Т. 13. №6. С.145-151.
- Демьяненко Е.Г., Тлустенко С.Ф., Попов И.П. Анализ технологических процессов отбортовки-формовки в системе LS-DYNA//Вестник СГАУ. 2006. №2. Часть 1. С. 282-286.
- Демьяненко Е.Г., Попов И.П. Штамп для изготовления тонкостенных сварных оболочек//Заготовительные производства в машиностроении. 2006. №12. С. 25-27.
- Хаймович, И.Н., Хаймович, А.И. Рационализация организации производства машиностроительного предприятия на основе реинжиниринга//Вестник СГАУ им. акад. С.П. Королева. Самара. 2006. №3. С.53-58.
- Хаймович, И.Н., Хаймович, А.И. Процедурные правила разработки и согласования бизнес-процессов кузнечно-штамповочного производства//Вестник СГАУ им. акад. С.П. Королева. Самара. 2008. №1. С.248-252.


