Разработка модели поверхностной волны зарядов затухающего коронного разряда

Самарский государственный аэрокосмический университет

Представлено аналитическое описание механизма формирования протяженных зарядовых структур, экспериментально наблюдаемых на односторонне фольгированных пленках диэлектрика, образующих разрядный промежуток с высоковольтным игольчатым электродом в воздухе атмосферного давления. Научная значимость исследуемых вопросов связана с решением фундаментальной проблемы стабилизации газовых разрядов в плотных средах.

Динамика расширения порошковых электрографических структур связывается с возбуждением волны зарядов, обусловленной выносом ионов поверхностного слоя слабоионизованного газа. Сделанные допущения сводят задачу к описанию процесса преобразования потенциального рельефа на электростатической мишени при облучении пучком отрицательных ионов. Использование в работе математического аппарата коронного разряда позволило получить уравнение, связывающее скорость расширения зарядовой структуры с нормальной к поверхности диэлектрика составляющей плотности тока ионов.

Отрицательная корона в воздушном промежутке между острием и плоскостью с высокоомной диэлектрической пленкой довольно быстро запирается из-за формирования на поверхности диэлектрика зарядового барьера. Однако в [1] были экспериментально получены динамические электрограммы в виде расходящейся волновой структуры, которые возбуждались в момент ослабления напряженности e электрического поля короны полем зарядового барьера. Характерная скорость распространения фронта порошковых подвижек на электрограммах составляла единицы см/с [2], что более, чем на порядок превосходит скорость растекания остаточных зарядов для подложки с поверхностным сопротивлением > 10¹⁴ Ом [3].

Связывая динамические электрограммы с выносом на подложку зарядов слабоионизованного поверхностного слоя газа в электрическом поле потенциального барьера, в данной работе сделана попытка аналитического описания поверхностного волнового процесса. Научная значимость исследуемых вопросов связана с решением фундаментальной проблемы стабилизации газовых разрядов в плотных средах.

Запишем систему уравнений, объединяющих процессы во внешней области коронного разряда с поверхностными процессами на подложке, в виде:

dpd- = - div r’(1)

р = (n + z +- n-z-)e6;(2)

j = (p+n+z ++ p-n-z")e0E ;(3)

divetE) = Р/ ;(4)

d^dt = -j •(5)

Здесь: p - объемная плотность зарядов в любой точке газа; j - плотность тока; _n ⁺ , _n ^- - объемная концентрация ионов; z ⁺ , z ^- -кратность зарядов ионов; p ⁺, p" - подвижность ионов; е₀ - элементарный заряд; е ₀ -электрическая постоянная; j z - нормальная составляющая плотности тока; о - поверхностная плотность зарядов на подложке.

В уравнении (5) не учтены поверхностные токи на диэлектрике, что допустимо, если поверхностное сопротивление пленки вели- ко. Уравнение (4) (теорема Гаусса в дифференциальной форме) заменяет уравнение Пуассона, которое легко получить из уравнения (4).

Диэлектрическая проницаемость газа принята равной g = 1 . При численной оценке примем параметры установки равными:

напряжение на острийном электроде

U 0 = - 5 кВ;

радиус острия r₀ = 50 мкм;

высота электрода над поверхностью диэлектрика h = 5 мм;

толщина диэлектрика d = 0,1 мм;

относительная проницаемость диэлектрика _е = 3 ;

толщина приповерхностного слоя сла-боионизованного газа l = 10 мкм;

подвижность ионов д ⁺ = д ^- = 2 см²/ (В - с)

Оценим отношение времени осаждения ионов из приповерхностного слоя на диэлек трик т 1 ко времени перемещения ионов от коротрона до диэлектрика т2 . Очевидно,

Подставив (7) в (1), получим:

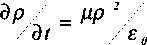
r

+ д E - grad р .      (8)

Будем считать известными для момента окончания разряда (t = 0 ) функции p°(r,z) ;

E°(r,z) ; о ⁰(r) .

Электрическое поле создается электродной системой, зарядами на диэлектрике и объемными зарядами rr r r

E = E , + E о + E р .

В процессе дозарядки пленки составля ющие Eо и Eр будут изменяться. Будем предполагать, что эти изменения невелики. Такое предположение оправдано, если суммарный объемный заряд меньше поверхностного заряда. Отсюда

E = E⁰ .             ⁽¹⁰⁾

Кроме того, положим р2 = р( р + Ар) » р - р0;     (11)

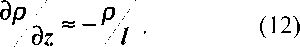
Уравнение (8) примет вид:

можно принять

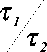
~ l/h ~ ² " ¹⁰ 3 • Так как

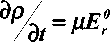
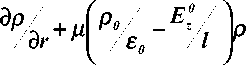
первый процесс протекает значительно быстрее второго, то процесс осаждения зарядов из приповерхностного слоя на диэлектрик является определяющим. Ясно, что сложная система уравнений (1)-(5) не может быть решена аналитически без упрощающих предположений.

Сделаем ряд допущений, возможно, довольно грубых, но которые позволят нам в более или менее удовлетворительной форме проанализировать процесс дозарядки пленки. Допустим, что в приповерхностном слое n ⁺ <<  n ^- и обозначим д ^- = д . Тогда уравнение (3) с учетом (2) примет вид:

r j = - дрE .            (6)

Из уравнений (6) и (4) получим:

rr div j = - д - div (рЕ) = rr

= - др - divE - д Е - grad p =

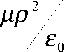
- д Е - grad p

Разделяем переменные. Для этого поло- жим р = T(t)f(r) .

Из (13) и (14) получим

1 T

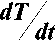
-а .

Неизвестная пока константа а должна быть больше нуля: а >  0 , иначе плотность зарядов будет неограниченно возрастать с течением времени, что не имеет физического смысла. Интегрируя (15) и учитывая, что при t ^^ р ^ 0 , получим

T = e-а.(16)

Из (14) и (16) при t = 0 получим

f(r) = р(г) .

Тогда р = Р0 - e-а.(18)

Подставив (18) в (13), получим

⁰ . ^др о/ ₌ Г ^z / \j _ ДО 0 / qx ^ E r /Вг ^ /1 - ар /е ₀ • ⁽¹⁹⁾ Это уравнение накладывает ограничение на задаваемые функции р_в , e⁰ , что есте

а =

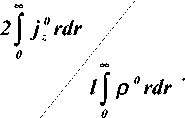
ственно, так как поле зависит от распределения р⁰ и 0⁰ •

Из (6) и (18) получим r r j = joe-а,(20)

где j = - др 0E0 •(21)

Подставив (20) в (5), получим

30£ = ’а,(22)

Постоянная времени

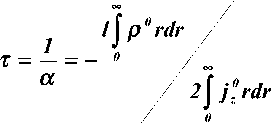
отсюда
а = а 0 +	Г ; 0 /Л j\4 V J	(e - a t - 1) •	(23)
Плотность осевших зарядов

Aa =

Граница пятна, как всегда, размыта, поэтому задавать ее можно только условно • Выбираем произвольно значение 0гр - плотность зарядов на границе пятна^ Тогда из (23) получим уравнение для границы пятна агр = а0 + j0(e"-1) •      (30)

Дифференцируя (30) по t , получим

d a

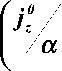
(e ^{- a t} - 1)

J

При t ^7 получим

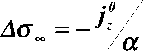
j 0 =- p^E» •

При вычислении плотности тока следу

ет учитывать, что р" зависит от координаты z • В выражениях (23), (24), (25) следует брать плотность зарядов на поверхности диэлект-

рика^ Там, где E_z <  0 , отрицательные заряды будут отталкиваться полем от поверхности, и следует считать р ⁰ = 0 • Там же, где

E_z >  0 , заряды прижимаются полем к поверхности, и следует считать р ⁰ = р - максимальным в слое^

Допустим, что все заряды в слое осядут на диэлектрик, тогда

dr

⁰              t dj⁰ t

- Г + т ( e ^А - 1)^Г - e ^А j® = 0 • (31) dr

Отсюда находим скорость расширения

пятна:

r

ãð

-

e

^т j

0 z

0              -t da / + т( e А -dr

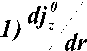
В процессе дозарядки пленки электрическое поле электродной системы играет стабилизирующую ролы Без него приповерхностный слой внутренними силами отталкивания рассеивался бы в окружающую среду, а не оседал на диэлектрике^

Рассмотренная модель поверхностной волны зарядов способствует развитию физических представлений о зарядовых барьерах, как о потенциальных электродах, позволяющих не только усиливать поле на границе зарядового пятна, но и регулировать уровень предыонизании приповерхностного слоя газа путем выноса на периферию диффузной фазы газового разряда^

1 ⁷ 0z_X-, .     7 j° ⁰ 2 п rdr Х

- J р ⁽r)2 K rdr = ^- J        / , (27)

где введена средняя плотность зарядов в слое р) =

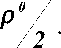
Отсюда