Разработка нейронных сетей для моделирования дифракции электромагнитного излучения на одиночном цилиндре и группе цилиндрических объектов

Развитие нанофотоники с одной стороны и вычислительных систем с другой обуславливает интерес к созданию методов и алгоритмов решения задач математической (строгой) теории дифракции. Традиционно для этого используются аналитический (метод Ми [1]) и численные подходы. К последним отнесем: FDTD-метод (Finite-Difference Time-Domain) [2], RCWA (Rigorous coupled-wave analysis) [3] и т.д. Значимым недостатком аналитического подхода является ограниченность случаев, при которых известно точное решение (дифракция на цилиндре, клине, шаре) [4]. К сдерживающему ограничению методов FDTD и RCWA относят их высокую вычислительную сложность и требования к памяти компьютера, значимые при рассмотрении двумерного случая и практически воспрещающие исследование сколь-нибудь протяженных элементов в трехмерном.

Выход из сложившейся ситуации ряд авторов видит в использовании нейронных сетей для решения задачи дифракции, причем разными авторами предлагаются разнообразные архитектуры и различные подходы к разработке и обучению таких сетей [5]. Так, в работе [6] рассматривается моделирование рассеивания электромагнитного поля идеально проводящими объектами, имеющими круговое или квадратное сечение. Авторами рассмотрен подход, подразумевающий использование рекуррентных нейронных сетей (RNN) для моделирования данного явления в рамках одного временного шага с предварительным обучением по

6179-CO-1640.

предыдущим шагам, дифракционная картина на которых вычислялась с помощью FDTD-метода. Рассмотрению подлежал двумерный случай дифракции TE-волны и небольшая сеточная область: 128 × 128 узлов по пространству. В качестве источника излучения выступает гауссовский импульс с частотой 2 ГГц либо плоская монохроматическая волна; геометрические размеры объекта меняются в пределах 0,4λ–0,6λ (радиус круга или сторона квадрата). В рамках данных ограничений ошибка решения, полученного с помощью нейронной сети, составила 5 %.

В работе [7] авторами рассматривается применение нейронных сетей к решению задачи рассеивания плоской монохроматической волны цилиндрическими диэлектрическими объектами с различными геометрией сечения и диэлектрической проницаемостью. Рассматривается как применение архитектуры U-Net, так и различных ее модификаций. Обучение нейронных сетей проходило на изображениях размером 128 × 128, полученных с помощью FDFD-метода (в отличие от прошлой статьи речь идет о квадрате модуля комплексной амплитуды поля, найденного для схожего, но другого объекта). В ходе серии вычислительных экспериментов демонстрируется преимущество архитектуры U-Net по точности в сравнении с другими архитектурами. Также показана универсальность данной сети: для объектов, имеющих в сечении форму, не представленную в обучающей выборке, ошибка решения составила 3,782%, а для объектов из материалов, показатель преломления которых не встречался в обучающей выборке, ошибка решения составила 8,6%.

В работе [8] авторами изучается вопрос применимости к решению задачи дифракции на объектах со сложной геометрией сечения графовых нейронных сетей (GNN). Монохроматический источник излучения характеризуется λ = 1 мкм; объект, на котором происходит дифракция, имеет произвольную форму, но фиксированную диэлектрическую проницаемость (ε = 2,1025); размеры изучаемой области также были ограничены тремя длинами волн. При обучении использовались наборы из пар изображений (180 × 180 пикселов); в одной паре изображения отстоят друг от друга на один временной шаг сеточной области (в отличие от первой работы, где использовалось большее количество временных шагов в одном объекте из набора, и второй работы, где сдвиги по временным шагам не использовались вовсе). В результате ошибка решения составила 3,2 %. Есть и иные публикации, представляющие схожие результаты при моделировании распространения электромагнитной волны в пространстве, но для отличной постановки задачи, например, [9].

Отдельно отметим работы, которые не связаны непосредственно с моделированием явления дифракции, однако также имеют отношение к регрессионным задачам и свойствам оптических элементов. В работе [10] рассматривается задача прогноза коэффициента пропускания двумерных щелевых решеток. Для решения такой задачи используется комбинация сверточных и полносвязных слоев: для обработки исходного изображения решетки используется набор сверточных и пуллинговых слоев, после чего полученные данные пропускаются через полносвязную сеть, выход которой представляет собой числовой вектор заранее определенной длины, содержащий в себе значения коэффициента пропускания для различных длин волн. В качестве показателя качества использовалась метрика R2, которая в ходе экспериментов составила 0,86.

В работе [11] рассматривается задача расчета Q-фактора фотонного кристалла по описанию его структуры. Рассматривается архитектура, похожая на таковую в предыдущей работе, однако сверточный кодер, помимо сверточных и пуллинговых слоев, содержит слои нормализации батча, а полносвязная сеть на выходе формирует одно число – прогноз Q-фактора. Точность решения при этом составила 99 %.

Перечисленные работы закладывают фундамент для развития предметной области. Так, работа [6] посвящена задаче рассеивания поля идеальными проводниками, что упрощает отыскание дифракционной картины, подразумевая отсутствие поля внутри оптического элемента. Случай диэлектрических элементов остается открытым для рассмотрения. В работе [7] авторами не уделяется внимание свойствам обучающей выборки и их влиянию на точность модели; более того, обучающие и тестовые данные охватывают лишь тот случай, когда длина волны падающего излучения сравнима с геометрическими размерами сечения объекта, на котором происходит дифракция. В [8], как и в [6], и вовсе прогноз модели делается лишь на один временной шаг. В работах [10] и [11] рассматриваются модели, не применимые в своем исходном виде к решению поставленной задачи, так как прогнозируют лишь одно число. Однако их развитие представляется весьма перспективным в силу высокого значения метрик качества и относительной простоты архитектур.

Целью авторов предлагаемой работы было повышение точности нейросетевого решения в случае дифракции плоской электромагнитной волны на цилиндре кругового сечения и наборе таких цилиндров. Последний случай в известных авторам работах не представлен вовсе.

1.    Модификация и сравнение архитектур нейронных сетей

Предварим описание архитектур нейронных сетей пояснением формата входных и выходных данных. Опираясь на [7], определим эти форматы следующим образом. Пусть на вход нейронная сеть принимает матрицу N×N, которая описывает распределение показателя преломления в изучаемой области. На выходе нейронной сети будем ожидать прогноз распределения интенсивности электрического поля в рассматриваемой области после прохождения электромагнитной волны через цилиндр, заданный упомянутой матрицей и расположенный в центре области.

Опираясь на пример нейронной сети из [7], рассмотрим следующую архитектуру (рис. 1).

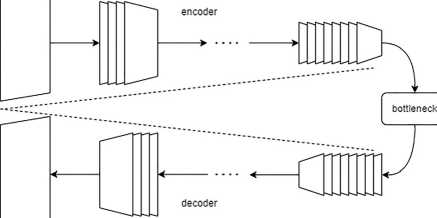
Рис. 1. Архитектура первой нейронной сети

Замысел авторской модификации состоит в следовании примерам из работ [12, 13], где предлагается архитектура residual-блоков (рис. 2) для решения задачи классификации изображений. В упомянутых работах демонстрируется целесообразность замены аппроксимируемой функции f ( x ) на функцию h ( x ) = f ( x ) – x , что помогает решить проблему затухания градиента и ускорить процесс обучения сети. Далее будет показана успешность такой замены и при решении задачи дифракции. При этом отметим, что в отличие от f ( x ) , представляющей собой некоторую функцию, которую должна аппроксимировать нейронная сеть, F(x) представляет собой набор операций непосредственно внутри блока (например, свертка или pooling).

Конструируя вторую сеть на основе работы [9], модифицируем предлагаемую в ней архитектуру (вместо одного числа на выходе должна появляться матрица N×N ) следующим образом: перед выходом сети добавим дополнительные полносвязные слои, последний из которых будет содержать N ² нейронов, после которых расположим Reshape-слой, который преобразует полученный одномерный массив длины N ² в квадратную матрицу N×N (рис. 3) .

Рис. 2. Структура residual-блока: в качестве F(x) обозначены все действия, которые производятся над входными данными

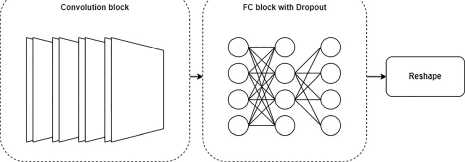
Рис. 3. Архитектура второй нейронной сети

Следуя за работой [11], рассмотрим архитектуру иного вида (третью предлагаемую здесь сеть). Пусть нейронная сеть имеет сверточные кодер и декодер, между которыми находится полносвязная сеть из трех слоев, а также после прохождения декодера данные пропускаются через двуслойную полносвязную сеть и преобразуются в необходимый формат (матрица N×N ). В чистом виде данная сеть из [11] неприменима к решению поставленной задачи. Главное отличие модифицированной модели от базовой состоит в добавлении слоев обратной свертки в качестве декодера, изменении параметров последнего полносвязного слоя и добавлении Reshape-слоя для приведения выходных данных к требуемому формату (рис. 4).

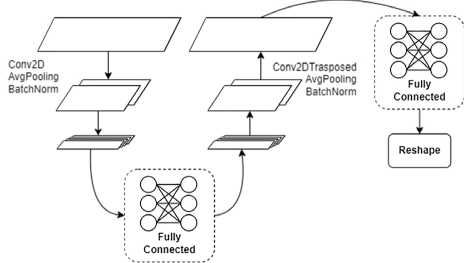
Рис. 4. Архитектура третьей нейронной сети

Для исследования и сравнения предложенных архитектур подготовим ряд обучающих наборов данных. Полагалось, что плоская монохроматическая TE-волна (λ = 1 мкм) падает на диэлектрический цилиндр кругового сечения. В первых наборах обучающих данных был зафиксирован радиус цилиндра R = λ, а значения показателя преломления материала цилиндра менялись в пределах показателей преломления различных стекол (от 1,46 до 1,9) [14]. Во вторых наборах, наоборот, фиксировался показатель преломления материала цилиндра n = 1,5, тогда как радиус цилиндра варьировался в границах от R = 0,1λ до R = 10λ. Отметим, что часть обучающих наборов составлена с той же идеей, что и в работе [7], т.е. подразумевает изменение показателя преломления материала; однако важным отличием является многообразие значений радиуса цилиндра, чего не было в упомянутых работах.

В каждом из упомянутых наборов объем обучающей выборки варьировался одинаково: от 5 до 89 изображений; выбирались не случайные значения варьируемых параметров в пределах допустимого диапазона (как, например, в [7]), а равномерно расположенные в его пределах. Делалось это с целью максимального охвата различных возможных случаев дифракционных паттернов даже для обучающих выборок небольших размеров. Все наборы данных были созданы в трех экземплярах, отличающихся друг от друга дискретизацией сеточной области и, следовательно, размером изображений: 64 × 64, 128 × 128 и 256 × 256. В обозреваемых ранее работах вопрос о влиянии дискретизации на качество не ставился. При этом отметим, что во всех упомянутых работах обучающие наборы данных были подготовлены с использованием численных методов на крайне грубых сетках, что вносит свою погрешность в решение, тогда как в ходе данного исследования использовались решения, полученные аналитически [4].

2.    Исследование влияния обучающей выборки на среднюю ошибку для случая одного цилиндра

Три нейронные сети из предыдущего параграфа были обучены на каждом из сгенерированных наборов обучающих данных. Для реализации использовался язык программирования Python, отличающийся простотой синтаксиса и предоставляющий интерфейсы для работы с библиотекой Tensorflow. Достаточной длительностью обучения, согласно поведению функции ошибки (а именно ее стабилизации на одном уровне), оказалось значение в 400 эпох при использовании оптимизатора Adam с параметром скорости обучения (learning rate) 10-4.

Первым этапом стало исследование влияния дискретизации сеточной области на ошибку моделей. Для корректного сравнения качества моделей будем использовать выражение для ошибки, приведенное в [7]. Для отдельного экземпляра будем вычислять ошибку по формуле

Error =

£ ₍i / J y true ( i , j ) - У ped ( i , ^j ) =/ =—i------i-----x100%,    (1)

£ (., j)l У»™ (1, j )| где ytrue(i, j) – истинное значение интенсивности электрического поля в узле с координатами (i, j), ypred(i, j) – спрогнозированное нейронной сетью значение интенсивности электрического поля в узле с координатами (i, j).

Под средней ошибкой будем понимать усредненное значение ошибки, вычисленной по формуле (1) для всех экземпляров тестового набора данных. Значения средней ошибки для каждой из нейронных сетей для обучающих наборов данных с разной дискретизацией сеточной области приведены в табл. 1.

Табл. 1. Средняя ошибка для разных размеров изображений

Нейронная сеть	Размер изображения
	64 × 64	128 × 128	256 × 256
Модель 1	49 %	54 %	36 %
Модель 2	16 %	16 %	16 %
Модель 3	10 %	8 %	7 %

На основании данных табл. 1 можно сделать вывод о том, что наблюдается общая тенденция к уменьшению средней ошибки решения при увеличении размеров изображения. При этом каждая из моделей по-своему реализует данную тенденцию. Так, средняя ошибка решения, полученного с помощью модели 1, сначала растет, а лишь потом значительно уменьшается. Первоначальный рост можно объяснить тем, что изображение становится более детализированным, из-за чего нейронная сеть начинает чаще ошибаться в мелких деталях. При этом последующий спад значения средней ошибки свидетельствует о стабилизации уровня детализации, который не только не вносит отрицательного влияния на качество решения, но и позволяет его повысить за счет того, что нейронная сеть может обнаружить дополнительные зависимости между пикселами изображения, которые не могли быть обнаружены на изображениях меньших размеров. Для второй модели вычислительные эксперименты показали одинаковую среднюю ошибку для изображений любых размеров, что говорит о нечувствительности данной модели к размеру изображений. Для третьей модели наблюдается монотонное уменьшение средней ошибки, что объясняется аналогично уменьшению ошибки для первой модели. Опираясь на общую тенденцию, далее будем проводить исследования только на изображениях размера 256 × 256.

В ходе следующего этапа исследования уделим внимание исследованию зависимости ошибки решения от объема обучающей выборки. Под объемом будем понимать количество изображений в обучающем наборе данных. Важность данного этапа обусловлена определяющим влиянием количества обучающих экземпляров на скорость обучения модели. Скорость обучения, в свою очередь, определяет целесообразность перехода от классических методов решения задачи дифракции к нейросетевым.

Табл. 2. Средняя ошибка для разного объема обучающего набора данных

Нейронная сеть	Объем обучающей выборки
	5	9	44
Модель 1	62 %	38 %	11 %
Модель 2	17 %	16 %	16 %
Модель 3	7 %	6 %	6 %

Из табл. 2 видно, что рост объема обучающей выборки ведет к уменьшению средней ошибки, что является ожидаемой закономерностью. Однако отметим тот факт, что для моделей 2 и 3 это уменьшение является незначительным (1 %). Объяснение данного результата авторы находят в особенностях составления обучающих наборов данных, а именно в равномерном расположении значений варьируемых параметров в пределах заранее определенного допустимого диапазона, что даже для выборок с небольшим количеством экземпляров позволило сохранить ключевые паттерны, тогда как нейронная сеть по ним смогла восстановить остальные. Опираясь на данный результат, далее будем проводить исследования на обучающем наборе данных объемом в 5 изображений.

Наконец, на третьем этапе исследования, определив единые параметры обучения (объем обучающей выборки и размер изображений), сравним между собой полученные модели. Для начала рассмотрим обучение на выборке, внутри которой радиус цилиндра фиксирован, а меняется материал. Как пример инфе-ренса [7] модели рассмотрим прогноз каждой из моделей для n = 1,46 (рис. 5).

Рис. 5. Инференсы моделей при n = 1,46

Так, качественно лучшим образом смогла аппроксимировать функцию распределения интенсивности электрического поля первая модель. При этом данная модель успешно смоделировала паттерн, незначительно отклоняясь от истинных значений (ошибка составила 6,4%). При этом отметим недостатки остальных моделей. Так, вторая модель демонстрирует паттерн, схожий с истинным, однако отличный от него количеством минимумов и максимумов как внутри цилиндра, так и вне его (ошибка для примера на рис. 5 составила 22,96%). Третья же модель не справилась с поставленной задачей (ошибка для примера на рис. 5 составила 55,9%).

Далее рассмотрим обучение на выборке, внутри которой фиксирован материал цилиндра, а меняется со- отношение его радиуса и длины волны падающего излучения. Сначала, как и в предыдущем случае, рассмотрим конкретные инференсы для R = 0,1^ (рис. 6).

Аналитическое решение             Модель 1

0.6667         0.6165         0.Э704         1.1222         1.2741

Рис. 6. Инференсы моделей при R = 0,1 Л

Качественное сравнение прогнозов модели с истинными значениями интенсивности электрического поля говорит о том, что хуже всех в данном случае справляется первая модель, показавшая лучший результат в предыдущем случае (для примера на рис. 6 ошибка превышает 100 %). Причиной ухудшения результата может являться тот факт, что в данном случае в силу малости радиуса цилиндра по сравнению с длиной волны падающего излучения наблюдается в основном внешнее поле дифракции, тогда как в предыдущем случае основной вклад в ошибку вносило внутреннее поле дифракции. То есть первая модель хорошо справляется с внутренним полем дифракции, но слабо подходит для моделирования внешнего. Вторая же модель показала себя лучше остальных в данном варианте использования: ошибка решения составляет 12,5%. У третьей модели серьезной проблемой является зашумленность изображения, что делает ее качество хуже по сравнению со второй моделью (ошибка для примера на рис. 6 составляет 15,26%).

Таким образом, по сравнению с работой [6] удалось уменьшить ошибку решения до 6,4% за счет модификации параметров обучающей выборки. Также получена ошибка 12,5% для задачи с варьируемым радиусом цилиндра, которая значительно отличается от постановок задач в известных работах.

3.    Случай нескольких цилиндров

Теперь рассмотрим случай, когда дифракция происходит не на одном цилиндре, а на их наборе. В дальнейшем планируется расширить данный случай на исследование распространения излучения в фотонно-кристаллических структурах. В известных авторам работах решение данной задачи с использованием нейронных сетей ранее не рассматривалось. В этом случае рассмотрим следующие три конфигурации: два цилиндра, расположенных вертикально, два цилиндра, расположенных горизонтально, и четыре цилиндра, центры которых расположены в вершинах квадрата (рис. 7). При этом под вертикальным расположением будем понимать такое, что на оба цилиндра падает неискаженная волна, а прямая, соединяющая центры сечений, параллельна фронту падающей волны. Под горизонтальным расположением будем подразумевать такое, что неискаженная волна падает только на один цилиндр, а прямая, соединяющая центры сечений, перпендикулярна фронту падающей волны.

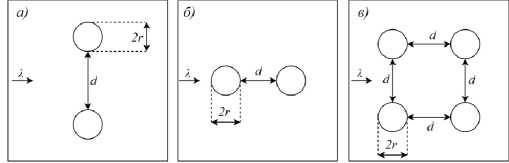
Рис. 7. Варианты расположения цилиндров:

(а) цилиндры расположены вертикально, (б) цилиндры расположены горизонтально, (в) центры цилиндров находятся в вершинах квадрата ; стрелкой с буквой Л показано направление распространения падающей волны

При этом будем считать, что длина волны падающего излучения фиксирована (λ = 1 мкм), а варьируемыми параметрами являются радиус цилиндра, расстояние между центрами цилиндров (для фотонных кристаллов его принято называть периодом) и показатель преломления материала цилиндра.

Далее каждая из ранее описанных моделей была обучена на наборе данных, содержащем результаты аналитического решения [14], основанного на теории Ми, для данных трех конфигураций цилиндров c различными значениями варьируемых параметров. Обучение каждой из сетей длилось 100 эпох. Отметим заодно длительность процесса обучения: для модели 1 она составила 62 с, для модели 2 – 45 с, для модели 3 – 57 с. При этом время подготовки обучающих данных составило 384 с. Графики изменения ошибки во время процесса обучения каждой из описанных ранее моделей приведены на рис. 8.

Далее на примере конфигурации из четырех цилиндров оценим качество каждой из моделей (рис. 9).

Ошибка решения в данном случае составляет 18,17%. Отметим, что в случае подачи на вход данной модели иных конфигураций (с отсутствием симметрии относительно обеих осей) результат оказывается искаженным и далеким от истинного распределения интенсивности электрического поля, что оставляет простор для дальнейших исследований.

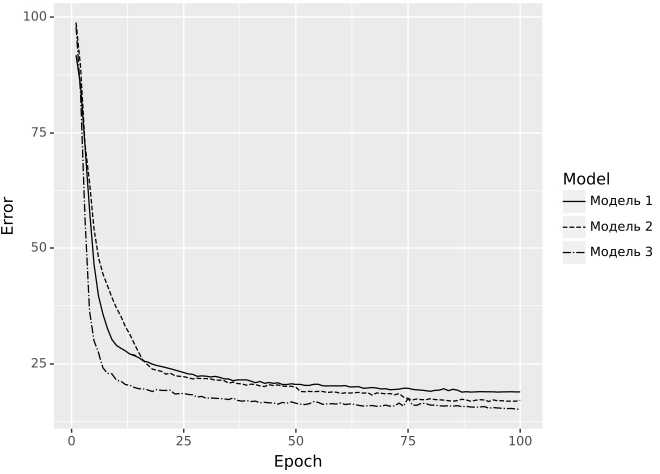
Рис. 8. Средняя ошибка для каждой из моделей

Отметим тот факт, что первая и третья модель справились с данной задачей хуже второй модели, как и в случае одного цилиндра при варьировании соотношения между радиусом цилиндра и длиной волны (ошибка составляет 26 % и 18,72 % соответственно для примера с рис. 9). При этом вторая модель неплохо справляется с изменением варьируемых параметров (ошибка составляет 14,25 % для примера с рис. 9). При этом отметим длительность инференса каждой из моделей: для модели 1 она составила 10,5 мс, для модели 2 – 1,09 мс, для модели 3 – 1,906 мс. При этом аналитические вычисления для аналогичного исследуемого случая занимают в среднем 62 мс, что на порядок больше лучшего результата для нейросетевого моделирования. На примере второй модели продемонстрируем прогноз для случая двух цилиндров (рис. 10).

Заключение

Таким образом, авторами показано, что различные подходы имеют свои достоинства и недостатки при решении задачи дифракции электромагнитного излучения как на одиночном цилиндрическом объекте, так и на группе таких объектов. А именно:

• 1)    для случая одного цилиндра средняя ошибка решения была уменьшена в 1,45 раз по сравнению с ранее достигнутыми результатами [6] за счет авторской модификации архитектуры. Также была рассмотрена ранее не встречавшаяся в литературе, но имеющая большое значение при исследовании фотонно-кристаллических структур постановка задачи для нейросетевого моделирования: дифракция на наборе цилиндров кругового сечения;

• 2)    при этом в случае набора цилиндров возникли новые вопросы, требующие внимания. Так, модель, основанная на использовании residual-блоков, характеризуется значительным ростом ошибки решения; модель, основанная на последовательном использовании сверточных и полносвязных слоев, отличается от нее в лучшую сторону.

0.002            0.840            1.679            2.517           3.356

Работа выполнена в рамках Государственного задания НИЦ «Курчатовский институт».

Аналитическое решение              Модель 1

Рис. 9. Примеры инференсов моделей в случае четырех цилиндров

Аналитическое решение              Модель 2

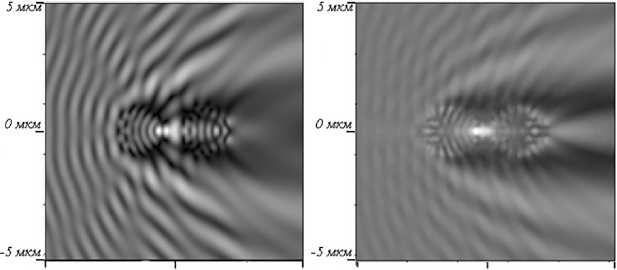
-5 мкм          Омхм           3 мкм -5 мкм          Омхм           5мкм

0.018           0.574           1.130          1.686           2.242

Рис. 10. Пример инференса второй модели для случая двух цилиндров