Разработка подхода к кластеризации студентов по уровню их творческого потенциала

Машинное обучение и интеллектуальный анализ данных заключают внутри себя большое количество законов и правил из других дисциплин, таких как математика, информатика и инженерия. Большинство алгоритмов машинного обучения используют формулы и законы теории вероятностей и математической статистики [1]. Поскольку объемы данных и возможные состояния системы велики, алгоритмы требуют оптимизации и увеличения вычислительной эффективности. Таким образом, для хорошо формализуемых алгоритмов используются методы функционального анализа, которые позволяют аппроксимировать функцию, являющуюся решением задачи при заданных параметрах выходной системы.

Анализ публикаций

Кластеризация, также известная как кластерный анализ, стала важной техникой в машинном обучении, используемой для обнаружения естественной группировки наблюдаемых данных. Задача кластеризации заключается в автоматическом разбиении объектов исходного множества данных на группы, кластеры, в зависимости от их схожести [2]. Схожесть объектов определяется расстоянием между объектами на основе выбранной для решения задачи метрики. Хоть и существует боль- шое множество различных метрик, ее выбор не является тривиальной задачей, поскольку на практике сходство объектов может быть довольно сложным. Задачу кластеризации решают следующие алгоритмы [3-5]:

• 1)    иерархические алгоритмы;

• 2)    k-средних;

• 3)    ФОРЕЛЬ;

• 4)    EM-алгоритм;

• 5)    алгоритмы нечеткой кластеризации.

Выбор методов кластерного анализа для прогнозирования успеваемости студентов

Целью настоящих исследований является получение эффективной модели кластеризации оценки уровня творческого потенциала студентов технических вузов.

Исходные данные для последующей кластеризации представляют собой результаты теста, в рамках которого стояла цель выяснить уровень творческого потенциала бакалавров технических вузов. Тест для оценки уровня творческого потенциала, включал в себя следующие блоки: интеллектуальный; коммуникативный; креативный; мотивационный; деятельностный.

Тестирование проходили 230 студентов, что подразумевает размер выборки данных равной в 230 объектов.

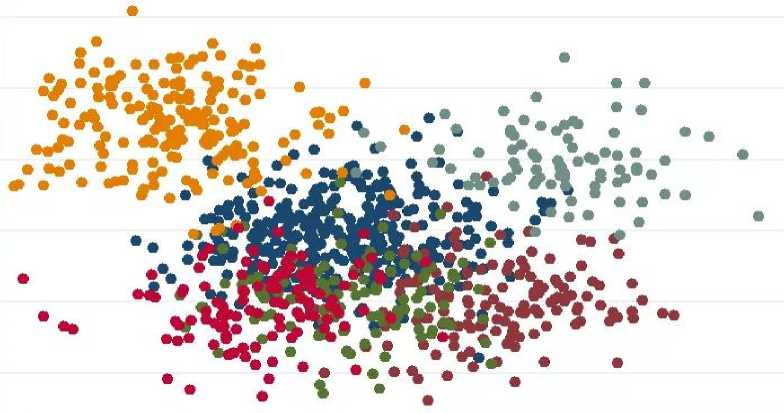
Рис. 1. Пример графического представления результатов кластеризации

Входными данными для кластеризации являются объекты, которые в свою очередь представлены в виде массива баллов за ответы по каждому из вопросов теста.

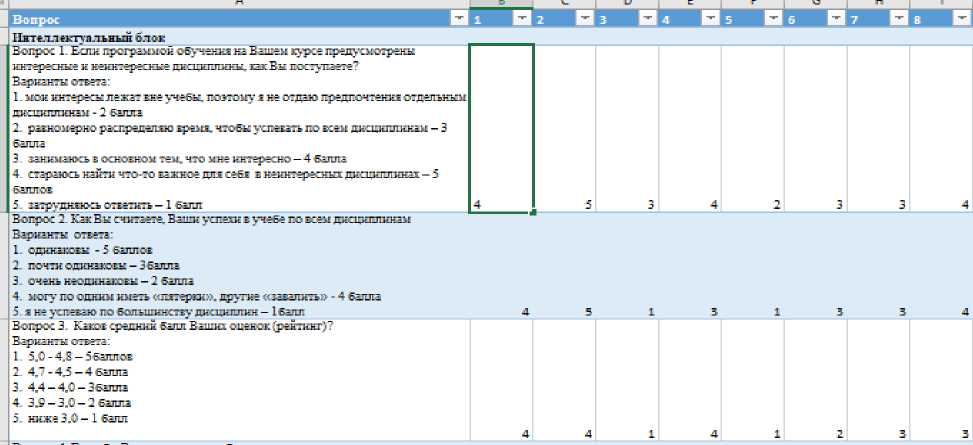
Рис. 2. Фрагмент собранных данных по тесту

В нашем исследовании использовались следующие алгоритмы кластеризации: к-средних, агломеративная кластеризация, кластеризация сдвига среднего.

К-средних. Целью данного неиерархического метода является разделения выборки на заранее известное количество кластеров k. Принцип его работы основан на итеративном перерасчёте центров кластеров, полученных на предыдущем шаге с последующим переразбиением выборки в соответствии новым центрам. Изначальные центры кластеров зачастую генерируются случайным образом. Процесс обуче- ния модели продолжается пока не прекратятся изменения расстояния между объектами и центрами внутри кластеров.

Агломеративная кластеризация. Данный алгоритм основан на иерархической кластеризации. Процесс начинается с создания нескольких групп, где каждая группа изначально содержит один объект. Затем происходит поиск наиболее похожих групп с последующим их объединением в одну группу. Модель обучается до тех пор, пока не будут получены единые группы наиболее похожих между собой объектов.

Кластеризация сдвига среднего. Алгоритм является непараметрическим, который итеративно присваивает объекты данных кластерам путём смещения точек в сторону «режима». Режимом является самая высокая плотность точек данных в пространстве признаков («регионе»).

Так как данные по тесту являются между собой соразмерными и их значения варьируются от 1 до 5, то преобразование и нормализация данных не требуется.

Практическая часть

Для построения моделей был выбран язык программирования Python. В силу своей простоты и логичности, данный язык программирование является хорошим средством реализации машинного обучения. Также стоит отметить обширный выбор готовых библиотек и фреймворков, что позволяет экономить время при решении задач.

Подключение необходимых библиотек Python

Numpy – это open-source модуль для Python, который предоставляет общие математические и числовые операции в виде пре-скомпилированных, быстрых функций. Они объединяются в высоко- уровневые пакеты. Matplotlib.pyplot это набор функций, которые позволяют matplotlib дублировать функционал MATLAB. Функционал данного пакета включает себя такие функции как: создание рисунков, создание области построения на рисунке, отображение объектов данных в этой области и т.п. Pandas считается классической библиотекой для обработки и анализа данных. В рамках функционала можно выделить: выгрузку данных, загрузку данных, нахождение статистических показателей и т.п.

Реализация алгоритмов кластеризации, описанных в теоретической части была осуществлена посредством библиотеки sklearn , внутри которой имеется множество уже готовых скриптов для решения задачи кластеризации. Описание выбранных алгоритмов в sklearn представлены ниже. В рамках решения задачи, данные были разбиты на количество кластеров: 2, 3, 4, 5.

Kmeans

Для того чтобы воспользоваться данным модулем, необходимо задать количество кластеров и загрузить данные. В первую очередь были загружены данные.

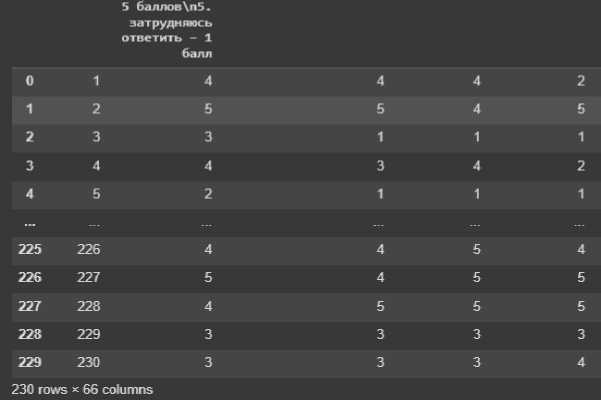
Рис. 3. Фрагмент загруженных данных

После загрузки данных была произведена кластеризации методом к-средних и получены результаты.

[3 333333333333333333333333333333333333 3333333311111111111111111111111111111 1111111111111111100000000000000000000 0000000000000000000000000004444444444 4444444444444444444444444444444444442 2222222222222222222222222222222222222 2222222 2]

Рис. 4. Результат работы Kmeans для 5 кластеров

На рисунке 4 представлен массив лейблов кластеров для каждого из 230 объектов.

Agglomerative Clustering

Для реализации алгоритма необходимо указать количества кластеров, до какого должны будут сбиваться в группы объекты, которые изначально каждый представляют собой отдельный кластер из одного объекта.

[3 333333333333333333333333333333333311 1331111111111111111111111111111111111 1111111111111144444444444444444444444 4444444222222222222222222222222222222 2222222222020020000000000000000000000 0000000000000000000000000000000000000 0000000 0]

Рис. 5. Результат работы AgglomerativeClustering для 5 кластеров

MeanShift

Также реализация данного непараметрического алгоритма была в диапазоне кластеров от 2 до 5. Для того чтобы полу- чать нужное количество кластеров, необходимо было настраивать параметр Квантилей.

number of estimated clusters : 5

[4 444444444444444444444444444444444444 4444444444444444444444444333333333333 3333333333333333333333322222222222222 2222222222222222222222221111111111111 1111111111111111111111111111000000000 0000000000000000000000000000000000000 0000000 0]

Рис. 6. Результат работы MeanShift для 5 кластеров

После реализации трёх выбранных алгоритмов, необходимо сохранить результаты. В качестве хранилища был выбран формат эксель листа.

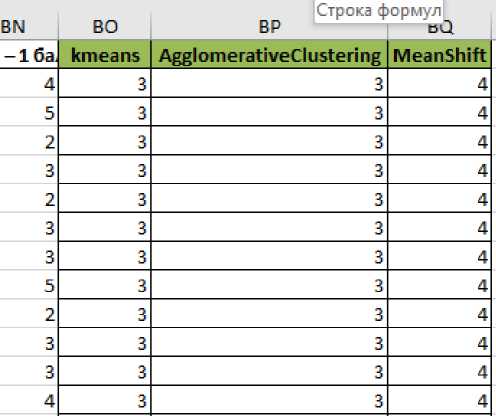
Рис. 7. Сохранённые результаты для 5 кластеров

Определение оптимального количества кластеров

В литературе было предложено множество мер для оценки результатов кластеризации. Проверка кластеризации использу- ется для разработки процедуры оценки результатов алгоритма кластеризации. В нашем исследовании мы использовали метод локтя и метод силуэта.

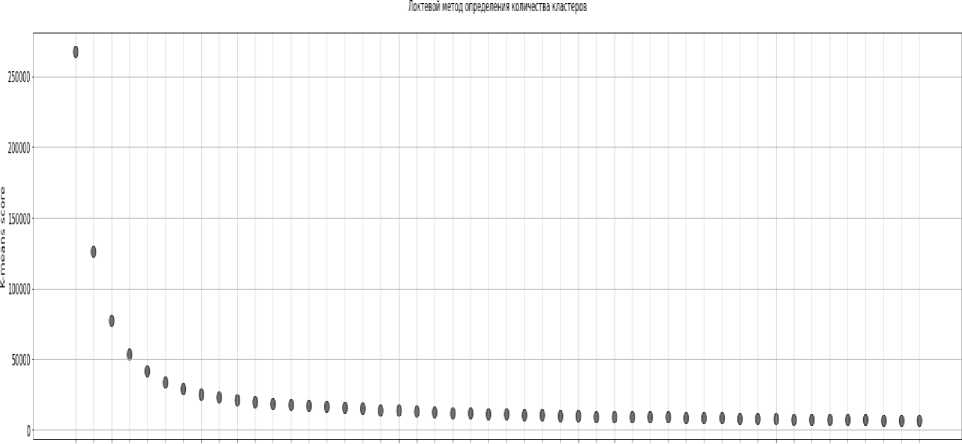
3 4 5 i ) 8 9 10 11 L? 13 14 15 16 :? 18 13 20 21 22 23 24 25 26 У 28 M 36 31 32 33 M 35 36 3? 38 В -10 11 42 43 44 45 46 47 Я И Кимер кластера

Рис. 11. Локтевой метод определения оптимального количества кластеров

Метод Elbow Curve показывает, как увеличение количества кластеров способствует разделению кластеров осмысленным образом, а не маргинальным. Изгиб указывает, что дополнительные кластеры за пределами пятого - шестого имеют небольшое значение.

Другая визуализация, которая может помочь определить оптимальное количе- ство кластеров, называется методом силуэта. Метод среднего силуэта вычисляет средний силуэт наблюдений для разных значений k. Оптимальным числом кластеров k является тот, который максимизирует средний силуэт в диапазоне возможных значений для k.

Мгоц коэффициента силуэта щи определения колияестаа кластеров

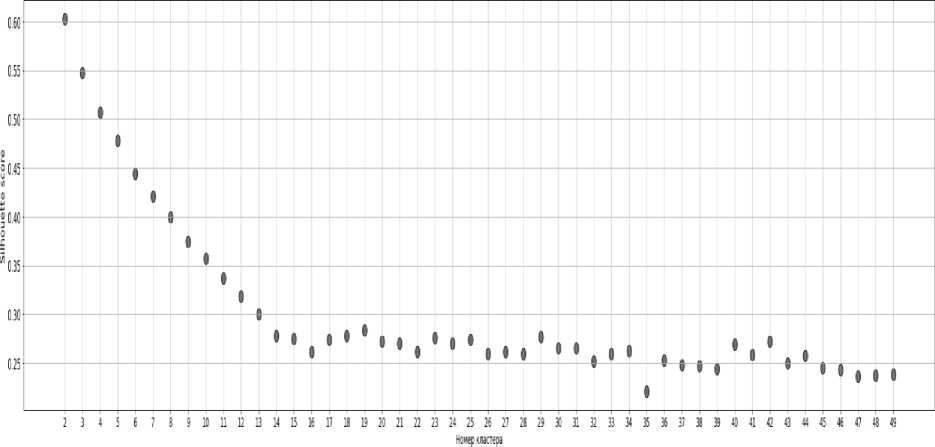
Рис. 12. Метод коэффициента силуэта для определения оптимального количества кластеров. Это также предполагает оптимальное количество из 5 кластеров.

Выводы. Был составлен и проведён тест-опросник, данные по которому затем были использованы для реализации не- скольких методов кластеризации с целью выявить неочевидные группы студентов с точки зрения творческого потенциала. Были получены результаты трёх алгоритмов, а именно: к-средних, агломеративная кла- стеризация, кластеризация сдвига среднего. По каждому алгоритму были собраны результаты для 2, 3, 4 и 5 кластеров и со- хранены для возможности последующего анализа результатов. Определено оптимальное количество кластеров. В дальнейшем планируется охарактеризовать каждый кластер.