Разработка прогнозных математических моделей качества радиоэлектронных средств по результатам автономных испытаний
Автор: Быков А.П., Пиганов М.Н.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.24, 2021 года.
Бесплатный доступ
В статье рассмотрена методика разработки прогнозной модели (оператора прогнозирования) качества бортовой аппаратуры методом экстраполяции. Показано, что наиболее оперативно информацию о качестве и надежности аппаратуры можно получить по результатам автономных испытаний. Сделан выбор объекта испытаний. В качестве объекта автономных испытаний был выбран микропроцессорный контроллер температуры. В качестве прогнозируемого параметра было выбрано переходное сопротивление между электрическими цепями микропроцессорного контроллера температуры. Приведены результаты обучающего эксперимента. Для построения оператора прогнозирования использованы квазидетерминированные модели линейного, логарифмического, экспоненциального и параболического вида. При разработке моделей использовалась нормировка прогнозируемого параметра по математическому ожиданию. Выбор прогнозных моделей основывался на критериях минимальной средней дисперсии, вычисленной при контрольных временных точках испытаний, и минимальных значениях вероятности ошибочных решений и риска потребителя. Проведено исследование разработанного оператора, получены вероятностные характеристики его эффективности.
Прогнозная модель, экстраполяция, квазидетерминированные модели, обучающий эксперимент, автономные испытаний, бортовой прибор
Короткий адрес: https://sciup.org/140256143
IDR: 140256143 | УДК: 621.382+629.78 | DOI: 10.18469/1810-3189.2021.24.1.39-47
Development of predictive mathematical models of the quality of radio electronic equipment based on the results of autonomous tests
The article discusses the methodology for developing a predictive model (forecasting operator) of the quality of onboard equipment using the extrapolation method. It is shown that the most efficient information about the quality and reliability of the equipment can be obtained from the results of autonomous tests. The choice of the test object was made. A microprocessor temperature controller was chosen as the object of autonomous tests. The transition resistance between the electrical circuits of the microprocessor temperature controller was chosen as a predicted parameter. The results of the training experiment are presented. To construct the forecasting operator, quasi-deterministic models of linear, logarithmic, exponential, and parabolic forms are used. When developing the models, the normalization of predicted parameter by mathematical expectation was used. The choice of predictive models was based on the criteria of minimum average variance, calculated at the test time points, and the minimum values of the probability of erroneous decisions and consumer risk. The research of the developed operator was carried out, probabilistic characteristics of its efficiency are obtained.
Текст научной статьи Разработка прогнозных математических моделей качества радиоэлектронных средств по результатам автономных испытаний
Постоянный рост сложности радиоэлектронных средств (РЭС), расширение их номенклатуры, переход к рыночным отношениям и ряд других факторов требует повышения требований к качеству выпускаемых изделий. Современные радиоэлектронные средства представляют собой сложный комплекс большого числа взаимосвязанных блоков, функциональных узлов и электронных компонентов. К РЭС космического назначения в первую очередь предъявляют требования высокой надежности, долговечности и безопасности. Достижение требуемого уровня этих характеристик невозможно без проведения ряда работ по подтверждению заданных ресурсных характеристик. Основной подход в решении этой задачи базируется на проведении натурных испытаний [1; 2]. Они включают большой комплекс исследований и контрольных операций необходимых для отработки электрических схем и конструкции РЭС, а также экспериментального подтверждения показателей надежности [3]. Анализ результатов испытаний является трудоемкой задачей и требует постоянной оптимизации и совершенствования этой процедуры. Большое значение имеет сокращение общей трудоемкости всех видов испытательных воздействий. Для этого требуется совер-
шенствование моделей и методик их проведения и оценки результатов. При этом целесообразно перенести центр тяжести с контроля и испытания готовых изделий на этап отработочных испытаний в процессе их проектирования [4]. Такие испытания позволяют своевременно внести изменения в схему, конструкцию и технологию изготовления бортовых РЭС космических аппаратов (КА).
Наиболее оперативно информацию о качестве и надежности бортовой аппаратуры КА можно получить по результатам автономных испытаний [5; 6].
Весьма актуальным остаются вопросы прогнозирования показателей качества и надежности бортовых РЭС КА по результатам испытаний. Решение этих вопросов сдерживается из-за отсутствия достаточно достоверных прогнозных математических моделей.
Целью данного исследования является разработка прогнозных математических моделей для оценки и прогнозирования качества и надежности РЭС по результатам автономных испытаний.
1. Анализ результатов испытаний
В качестве объектов испытаний были выбраны командная радиолиния, микропроцессорный контроллер температуры (МКТ) и система приема и преобразования информации КА. В данной статье
Таблица 1. Значение Δ R / R , %
Table 1. Δ R / R value, %
|
№ |
Класс |
25 ч |
100 ч |
250 ч |
500 ч |
1000 ч |
|
1 |
1 |
4 |
12 |
29 |
40 |
44 |
|
2 |
1 |
5 |
14 |
30 |
41 |
49 |
|
3 |
2 |
4 |
15 |
36 |
47 |
53 |
|
4 |
1 |
3 |
10 |
18 |
22 |
27 |
|
5 |
1 |
2 |
11 |
20 |
25 |
31 |
|
6 |
2 |
2 |
15 |
33 |
46 |
59 |
|
7 |
2 |
3 |
15 |
35 |
44 |
62 |
|
8 |
1 |
4 |
13 |
27 |
33 |
40 |
|
9 |
1 |
2 |
12 |
27 |
32 |
36 |
|
10 |
1 |
2 |
12 |
19 |
25 |
28 |
|
11 |
1 |
1 |
13 |
26 |
30 |
35 |
|
12 |
2 |
3 |
16 |
31 |
48 |
63 |
|
13 |
1 |
3 |
10 |
18 |
23 |
29 |
|
14 |
2 |
3 |
14 |
32 |
47 |
61 |
|
15 |
1 |
2 |
9 |
25 |
29 |
34 |
|
16 |
2 |
4 |
17 |
31 |
44 |
58 |
|
17 |
1 |
5 |
11 |
21 |
26 |
30 |
|
18 |
2 |
6 |
16 |
30 |
43 |
55 |
|
19 |
1 |
2 |
14 |
19 |
23 |
26 |
|
20 |
2 |
4 |
16 |
41 |
49 |
66 |
|
21 |
1 |
3 |
10 |
20 |
26 |
33 |
|
22 |
2 |
5 |
15 |
32 |
41 |
57 |
|
23 |
2 |
4 |
15 |
33 |
45 |
56 |
|
24 |
1 |
4 |
10 |
25 |
28 |
34 |
|
25 |
2 |
6 |
18 |
29 |
51 |
72 |
|
26 |
2 |
5 |
16 |
36 |
50 |
68 |
|
27 |
1 |
3 |
11 |
24 |
32 |
38 |
|
28 |
2 |
4 |
19 |
40 |
46 |
70 |
|
29 |
2 |
5 |
16 |
42 |
48 |
71 |
|
30 |
1 |
3 |
14 |
28 |
33 |
41 |
|
31 |
2 |
3 |
21 |
33 |
49 |
64 |
|
32 |
1 |
3 |
13 |
27 |
40 |
47 |
|
33 |
2 |
4 |
14 |
30 |
41 |
52 |
|
34 |
1 |
1 |
9 |
18 |
24 |
32 |
|
35 |
1 |
2 |
9 |
20 |
33 |
43 |
|
X |
3,4 |
13,571429 |
28,142857 |
37,257143 |
47,542857 |
|
|
а 2 |
1,6588235 |
8,7815126 |
46,12605 |
91,961345 |
216,13782 |
|
|
δ |
1,2879532 |
2,9633617 |
6,7916162 |
9,5896478 |
14,701626 |
Таблица 2. Результаты классификации
Table 2. Classification results
|
Вид квазидетерминированной модели |
||||
|
Линейная |
Логарифмическая |
Экспоненциальная |
Параболическая |
|
|
ош |
0,343 |
0,086 |
0,457 |
0,429 |
|
р потр |
0 |
0,136 |
0,457 |
0,441 |
|
р изг |
0,429 |
0,122 |
0 |
0 |
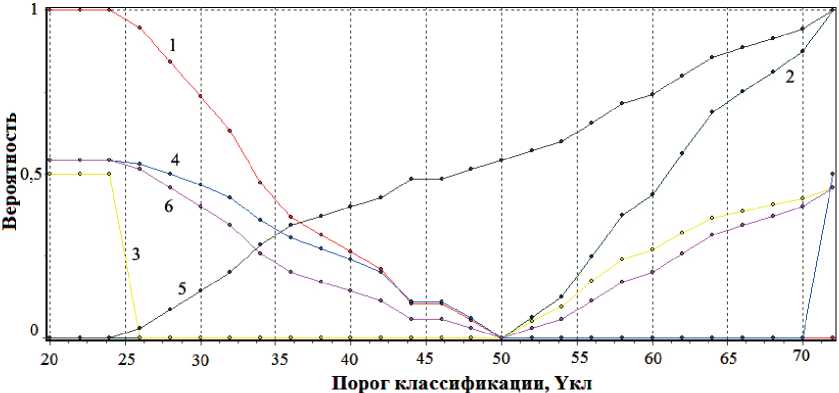
Рис. 1. Влияние порога классификации на вероятность ошибочных решений и другие характеристики
Fig. 1. Influence of the classification threshold on the probability of erroneous decisions and other characteristics
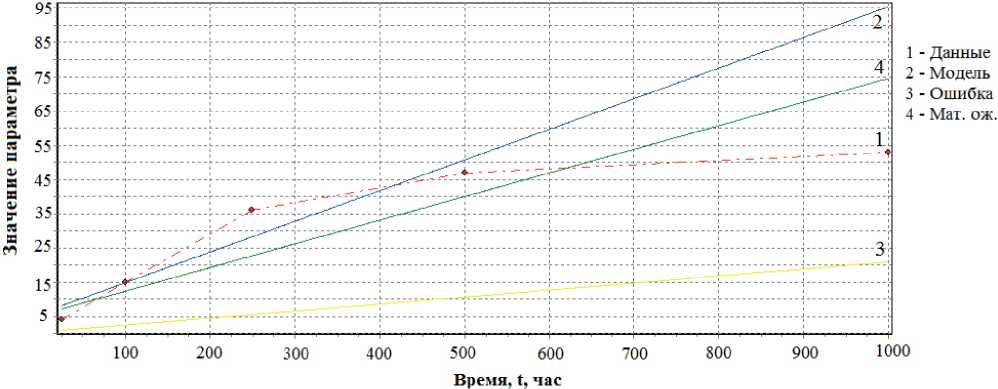
Рис. 2. Временная зависимость прогнозируемого параметра Δ R / R по линейной модели и результатам испытаний для 3-го экземпляра выборки
Fig. 2. Time dependence of the predicted parameter Δ R / R according to the linear model and test results for 3 samples of the sample
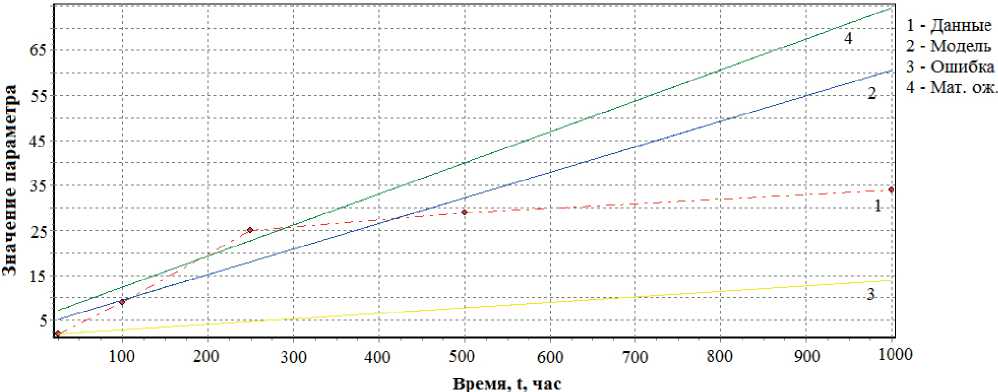
Рис. 3. Временная зависимость прогнозируемого параметра Δ R / R по линейной модели и результатам испытаний для 15-го экземпляра выборки
Fig. 3. Time dependence of the predicted parameter Δ R / R according to the linear model and test results for 15 instances of the sample
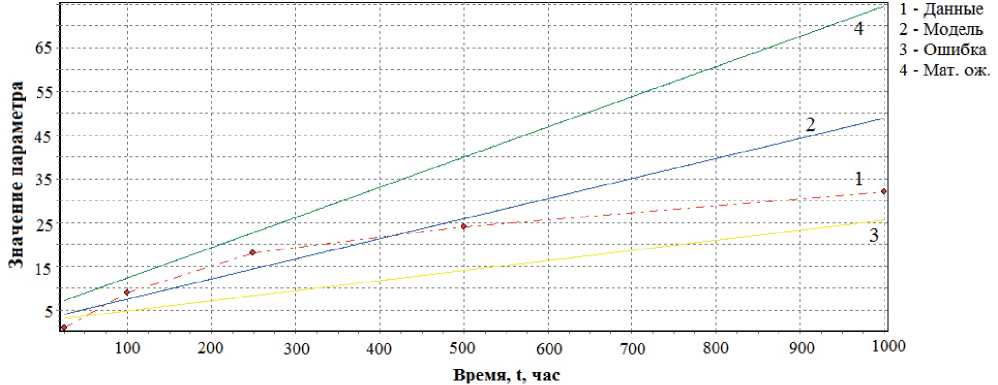
Рис. 4. Временная зависимость прогнозируемого параметра Δ R / R по линейной модели и результатам испытаний для 34-го экземпляра выборки
Fig. 4. Time dependence of the predicted parameter Δ R / R according to the linear model and test results for 34 instances of the sample
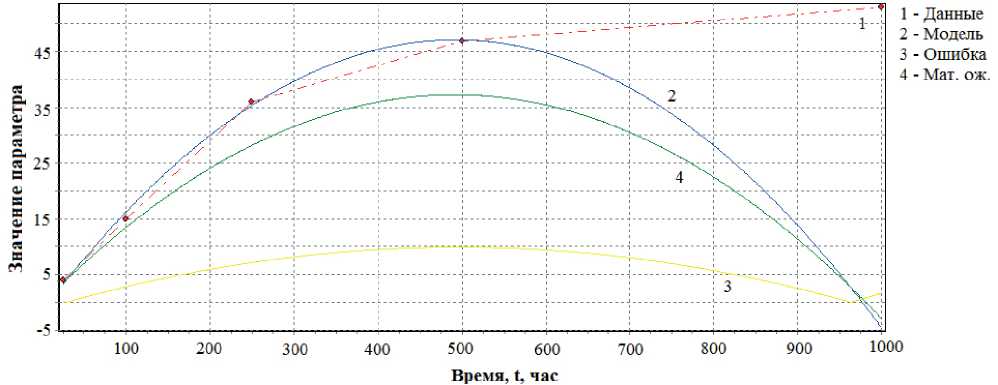
Рис. 5. Временная зависимость прогнозируемого параметра Δ R / R по параболической модели и результатам испытаний для 3-го экземпляра выборки
Fig. 5. Time dependence of the predicted parameter Δ R / R according to the parabolic model and test results for 3 instances of the sample
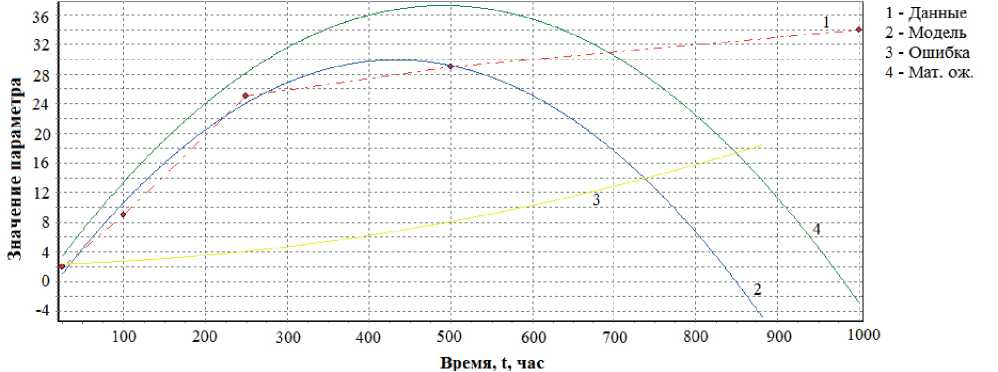
Рис. 6. Временная зависимость прогнозируемого параметра Δ R / R по параболической модели и результатам испытаний для 15-го экземпляра выборки
Fig. 6. Time dependence of the predicted parameter Δ R / R according to the parabolic model and test results for 15 instances of the sample
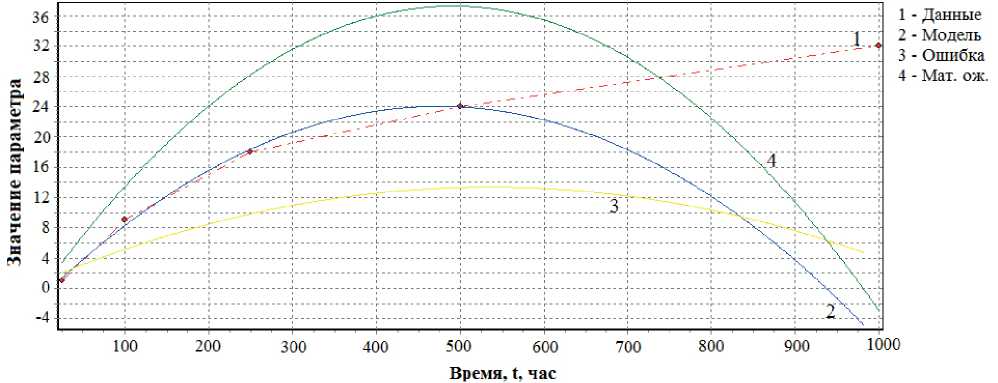
Рис. 7. Временная зависимость прогнозируемого параметра Δ R / R по параболической модели и результатам испытаний для 34-го экземпляра выборки
Fig. 7. Time dependence of the predicted parameter Δ R / R according to the parabolic model and test results for 34 instances of the sample
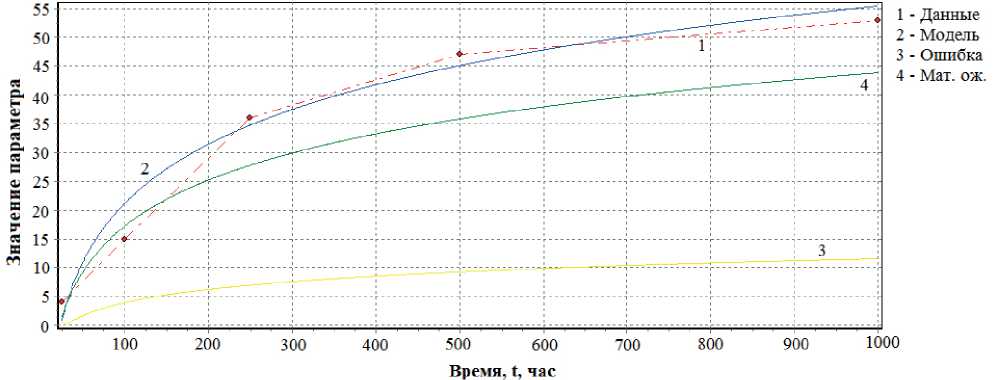
Рис. 8. Временная зависимость прогнозируемого параметра Δ R / R по логарифмической модели и результатам испытаний для 3-го экземпляра выборки
Fig. 8. Time dependence of the predicted parameter Δ R / R according to the logarithmic model and test results for 3 instances of the sample
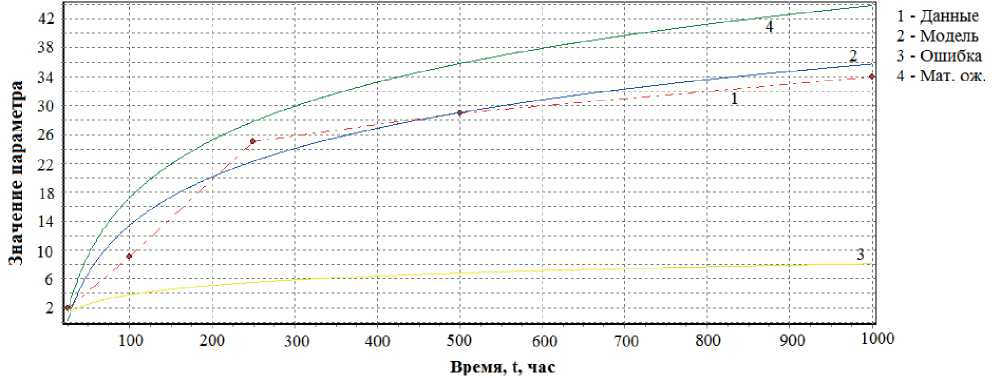
Рис. 9. Временная зависимость прогнозируемого параметра Δ R / R по логарифмической модели и результатам испытаний для 15-го экземпляра выборки
Fig. 9. Time dependence of the predicted parameter Δ R / R according to the logarithmic model and test results for 15 instances of the sample
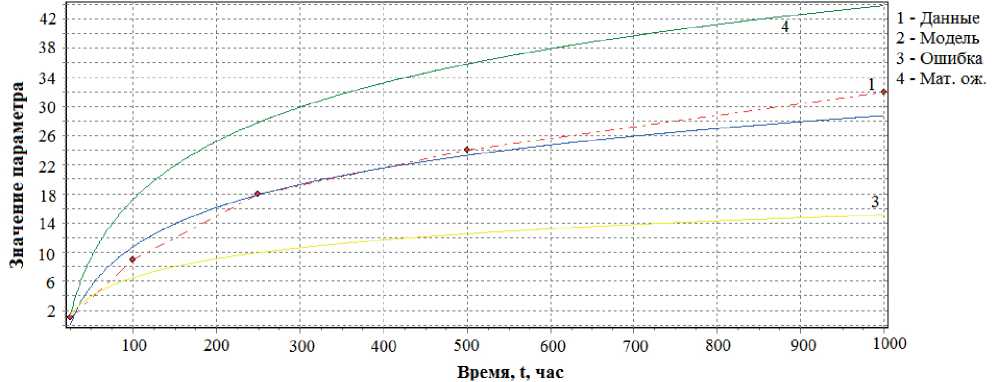
Рис. 10. Временная зависимость прогнозируемого параметра Δ R / R по логарифмической модели и результатам испытаний для 34-го экземпляра выборки
Fig. 10. Time dependence of the predicted parameter Δ R / R according to the logarithmic model and test results for 34 instances of the sample
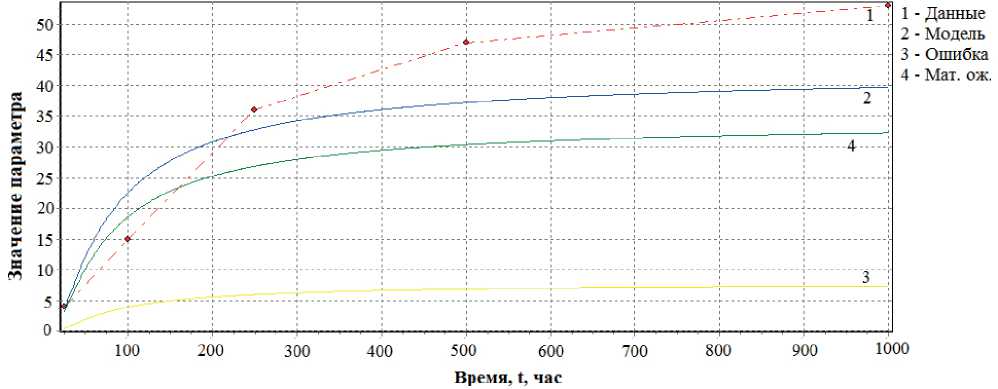
Рис. 11. Временная зависимость прогнозируемого параметра Δ R / R по экспонециальной модели и результатам испытаний для 3-го экземпляра выборки
Fig. 11. Time dependence of the predicted parameter Δ R / R according to the exponential model and test results for 3 instances of the sample
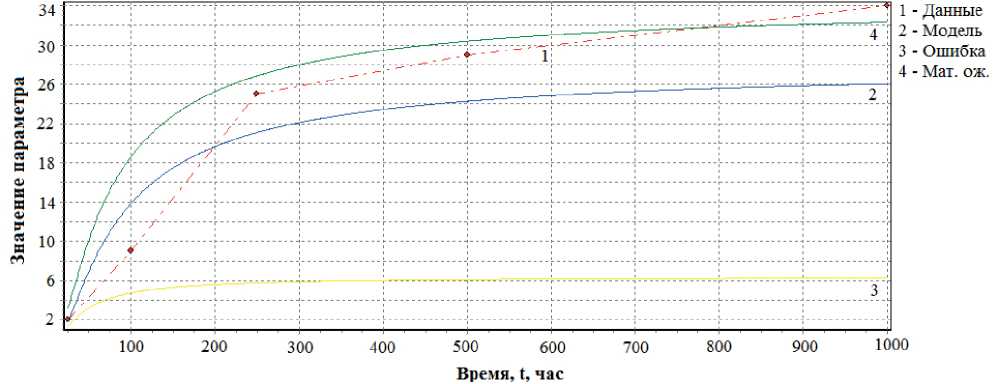
Рис. 12. Временная зависимость прогнозируемого параметра Δ R / R по логарифмической модели и результатам испытаний для 15-го экземпляра выборки
Fig. 12. Time dependence of the predicted parameter Δ R / R according to the logarithmic model and test results for 15 instances of the sample
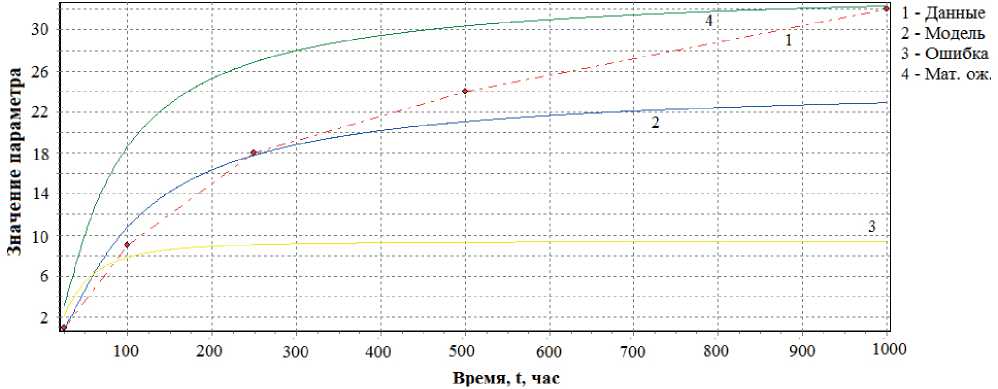
Рис. 13. Временная зависимость прогнозируемого параметра Δ R / R по логарифмической модели и результатам испытаний для 3-го экземпляра выборки
Fig. 13. Time dependence of the predicted parameter Δ R / R according to the logarithmic model and test results for 3 instances of the sample
Список литературы Разработка прогнозных математических моделей качества радиоэлектронных средств по результатам автономных испытаний
- Колесников А.В. Испытания конструкций и систем космических аппаратов. М.: Изд-во МАИ, 2007. 105 с.
- Kolesnikov A.V. Testing of Structures and Systems of Spacecraft. Moscow: Izd-vo MAI, 2007, 105 p. (In Russ.)
- Федоров В.К., Сергеев Н.П., Кондрашин А.А. Контроль и испытания в проектировании и производстве радиоэлектронных средств. М.: Техносфера, 2005. 504 с.
- Fedorov V.K., Sergeev N.P., Kondrashin A.A. Control and Testing in the Design and Production of Radio Electronic Equipment. Moscow: Tehnosfera, 2005, 504 p. (In Russ.)
- Лисейкин В.А., Моисеев Н.Ф., Фролов О.П. Основы теории испытаний. Экспериментальная отработка ракетно-космической техники. М.: Машиностроение-Полет; Виарт Плюс, 2015. 260 с.
- Lisejkin V.A., Moiseev N.F., Frolov O.P. Foundations of Test Theory. Experimental Development of Rocket and Space Technology. Moscow: Mashinostroenie-Polet; Viart Pljus, 2015, 260 p. (In Russ.)
- Бахвалов Ю.О. Испытания ракетно-космической техники. М.: АИР, 2015. 227 с.
- Bahvalov Yu.O. Testing of Rocket and Space Technology. Moscow: AIR, 2015, 227 p. (In Russ.)
- Быков А.П. Алгоритм проведения автономных испытаний радиоэлектронных средств // Физика волновых процессов и радиотехнические системы. 2020. Т. 23, № 3. С. 97-104. DOI: 10.18469/1810-3189.2020.23.3.97-104
- Bykov A.P. Algorithm for conducting autonomous tests of radio electronic means. Physics of Wave Processes and Radio Systems, 2020, vol. 23, no. 3, pp. 97-104. 10.18469/1810-3189.2020.23.3.97-104 (In Russ.) DOI: 10.18469/1810-3189.2020.23.3.97-104(InRuss.)
- Быков А.П., Андросов С.В., Пиганов М.Н. Методика тепловакуумных испытаний приборов космического аппарата // Надежность и качество сложных систем. 2019. № 3 (27). С. 78-83. DOI: 10.21685/2307-4205-2019-3-9
- Bykov A.P., Androsov S.V., Piganov M.N. Technique for thermal vacuum testing of spacecraft instruments. Nadezhnost' i kachestvo slozhnyh sistem, 2019, no. 3 (27), pp. 78-83. 10.21685/2307-4205-2019-3-9 (In Russ.) DOI: 10.21685/2307-4205-2019-3-9(InRuss.)
- Быков А.П., Пиганов М.Н. Методика автономных испытаний бортовых радиоэлектронных приборов космических аппаратов // Труды МАИ. 2020. № 111. DOI: 10.34759/trd-2020-111-7
- Bykov A.P., Piganov M.N. Method of autonomous testing of on-board radio electronic devices of spacecraft. Trudy MAI, 2020, no. 111, 10.34759/trd-2020-111-7 (In Russ.) DOI: 10.34759/trd-2020-111-7(InRuss.)
- Пиганов М.Н. Индивидуальное прогнозирование показателей качества элементов и компонентов микросборок. М.: Новые технологии, 2002. 267 с.
- Piganov M.N. Individual Prediction of Quality Indicators of Elements and Components of Microassemblies. Moscow: Novye tehnologii, 2002, 267 p. (In Russ.)
- Мишанов Р.О., Пиганов М.Н. Разработка прогнозной модели качества полупроводниковых приборов методом экстраполяции // Известия Самарского научного центра Российской академии наук. 2014. Т. 16, № 4 (3). С. 594-599. URL: http://www.ssc.smr.ru/izv_2014_4.html
- Mishanov R.O., Piganov M.N. Development of a predictive model for the quality of semiconductor devices by extrapolation. Izvestija Samarskogo nauchnogo tsentra Rossijskoj akademii nauk, 2014, vol. 16, no. 4 (3), pp. 594-599. URL: http://www.ssc.smr.ru/izv_2014_4.html (In Russ.)
