Разработка программного комплекса для моделирования гидродинамических течений методом сглаженных частиц

В современном мире важной частью любой сферы деятельности человека, будь то наука или производство, является компьютерное моделирование. Различные отрасли промышленности основываются на применении каких-либо физических явлений, и в эпоху активного развития вычислительных технологий возникает необходимость моделирования физических процессов при помощи вычислительной техники. Примером та- ких задач является моделирование динамики поверхностных вод и деформации дна1для выяснения степени влияния разработки карьеров на речное судоходство [7]. Для упрощения задач, связанных с симуляцией физических процессов, используются различные вычислительные методы компьютерного моделирования. Одним из таких методов является метод гидродинамики сглаженных частиц, сокращенно SPH.

Ключевая концепция SPH заключается в том, что значение функции в конкретной точке области оценивается из соседних точек с помощью ядра сглаживания. Для этого вводятся точки интерполяции, которые движутся вместе с потоком. Точки интерполяции также несут в себе массу и другие свойства. Особенностью метода является то, что жидкость делится на дискретные частицы, имеющие параметр так называемой длины сглаживания, обозначаемой в формулах как h [8].

Первым шагом необходимо ввести функцию ядра сглаживания

W(x´ – x, h), где h – радиус сглаживания.

Таким образом, получается следующая интерполяция функции f(r):

A ( x ) = ∫ A ( r ′ ) W ( r ′ - r , h ) dr ′ .

Существует много вариантов функций, удовлетворяющих условиям, которые можно использовать в качестве ядра [3]. Далее приведены примеры функций ядра, использованные в данной работе.

Для плотности:

wc ³¹⁵ I (/i⁹ - r²)³,0 < r 1 64я/1⁹ (.0, в остальных случаях

Для силы давления жидкости на частицу:

15 ( ^fr./i) = Тб

(h — r)³,0 < r <  h

0, в остальных случаях"

Для учета вязкости в жидкости:

2л h³

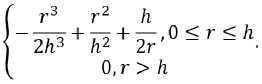
W(r, /1)

На следующем шаге производится замена интегрирования суммированием по соседним частицам ( m_i – масса частицы i, A_i – значение величины A для частицы, с_i – плотность, связанная с частицей, и W – функция ядра):

Алгоритм расчета представлен в виде блок-схемы на рисунке 1.

Значимым моментом является то, что можно использовать ядро, которое является дифференцируемым, для применения различ-

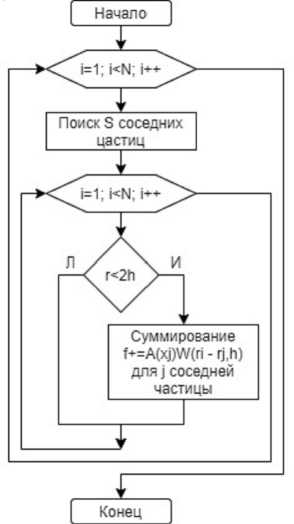
Рис. 1. Алгоритм расчета

ных дифференциальных операторов. Производные могут быть получены обычным дифференцированием, нет необходимости использовать сетку. Например, если нам нужно найти ∇ A(r) :

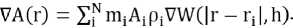
Уравнения газовой динамики [6], описы- вающие законы сохранения, имеют следующий вид:

dp dt du dt de dt

-pVu,

-p^

--Vil,

p

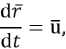
где r – вектор перемещения, t – время, ρ – плотность, u – вектор скорости, ∈ – удельная внутренняя энергия, p – давление [4].

Применяя метод к уравнениям газовой динамики, мы получим следующие уравнения для каждой частицы:

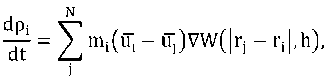
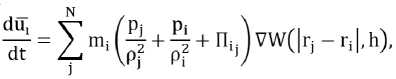
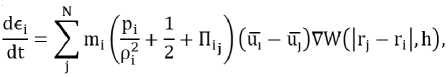
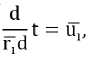
где П^- – искусственная вязкость.

Для реализации численного метода SPH были составлены отдельные алгоритмы расчета конкретных параметров частиц. Общая структура расчетной части состоит из нескольких последовательных функций расчета параметров частиц, выполняющихся в цикле для каждого момента времени.

Для реализации численного метода SPH было решено использовать язык программирования C++. Выбор именно этого языка обусловлен его достоинствами, среди которых можно выделить следующие:

– быстродействие;

– возможность работы с параллельным стандартом OpenMP;

– элементы объектно-ориентированного программирования;

– универсальность;

– официальная поддержка стандартов языка.

Относительно высокая скорость работы C++ является главным его преимуществом перед другими современными языками программирования при использовании в сфере компьютерного моделирования для реализации трудоемких вычислительных алгоритмов. Для еще большего ускорения работы вычислительных программ можно применить технологии параллельных вычислений. Так, в данной работе был выбран открытый стандарт для распараллеливания программ OpenMP. Преимуществом использования OpenMP является простота создания параллельной версии на основе уже готового последовательного кода программы [1].

Программный комплекс, реализующий метод гидродинамики сглаженных частиц, должен представлять собой совокупность нескольких модулей, взаимодействующих между собой и выполняющих каждый свою задачу.

Расчетные модули являются наборами классов и функций, которые используются и вызываются в объединяющем их интерфейсном модуле. Для создания расчетного модуля были разработаны специальные классы, используемые для расчетов – класс двухмерного вектора и класс частицы.

Объектно-ориентированный подход позволяет удобно работать с частицами как с отдельными экземплярами класса, со своими параметрами у каждой отдельно взятой частицы.

Класс частицы представляет собой набор переменных, задающих физические параметры частиц. Данный класс имеет семь основных переменных:

– масса;

– плотность;

– радиус сглаживания;

– давление;

– вектор скорости частицы;

– вектор суммы сил, действующих на частицу;

– координаты частицы.

Класс двухмерного вектора представляет собой две координаты: X и Y . Также класс содержит в себе перегруженные операторы для удобной работы с векторами. При написании класса были перегружены основные арифметические операторы:

– присваивание;

– сложение двух векторов;

– вычитание двух векторов;

– умножение вектора на скаляр;

– деление вектора на скаляр.

Общая структура программы должна состоять из нескольких взаимодействующих друг с другом модулей – модулей расчета параметров частиц и модуля интерфейса для взаимодействия с пользователем. Модуль интерфейса должен получать от пользователя параметры для частиц и выводить на экран визуализацию результата. Структура программы представлена в виде диаграммы на рисунке 2.

Интерфейс должен иметь поля для ввода начальных параметров эксперимента, а также специальную область для вывода графической визуализации расчетов на экран пользователю.

Тестирование разработанного программного комплекса проводилось на персональном компьютере со следующими характеристиками:

– процессор: AMD Ryzen 5 1600 3.2 GHz 6 ядер 12 потоков,

– оперативная память: 8 Гб,

– видеокарта NVIDIA: GeForce GTX 1050 1290 MHz.

Тестирование проводилось на примере задачи о падении дамбы с разным количеством частиц. Суть задачи заключается в том, что до начального момента времени эксперимента T0 две области пространства с разными характеристиками разделены тонкой стеной. В момент времени T0 стену убирают. В случае тестирования программы в отдельной части пространства размещается столб из заданного количества частиц. После старта начинается расчет всех показателей и положения частиц, на каждую из них начинают действовать соседние частицы и гравитация.

Проверка работы программы проводилась путем эксперимента с 200, 500 и 1000 частицами в режиме последовательного и параллельного расчетов.

Правильность работы программы оценивалась путем сравнения полученной визуализации с аналогичным экспериментом, описанным в статьях нескольких исследователей. В данной работе приводится сопоставление визуализации работы метода из статьи К.Е. Афа-

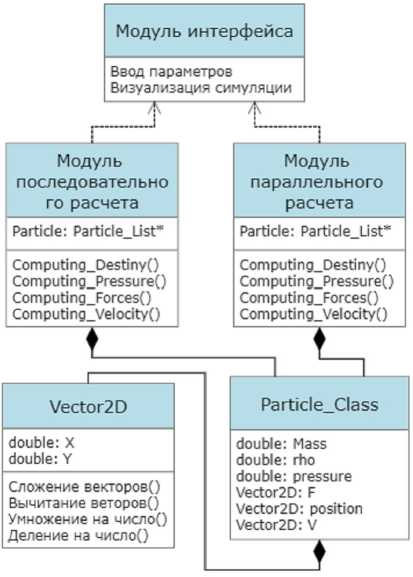
Рис. 2. Диаграмма структуры программы

насьева [8]. Прямое сравнение результатов при использовании 500 и 1500 частиц представлено на рисунке 3.

В ходе эксперимента, сразу после начала расчетов, на частицы начинает действовать сила тяжести, из-за чего частицы стремятся двигаться вниз, создавая давление друг на друга. Вследствие взаимного давления столб частиц начинает обрушаться. Частицы устремляются в свободное пространство справа от места размещения столба жидкости. По достижению волной частиц стенки, ограничивающей поле эксперимента, данная волна разбивается о граничную стенку, образуя всплеск частиц, устремленный вверх.

На основе полученных замеров времени работы программы был сделан вывод о существенном увеличении быстродействия вычислений. По графику зависимости времени вычислений от количества частиц на рисунке 4 видна разница в быстродействии. В работе Е.И. Николаева, описывающей эксперименты с применением метода SPH, приводятся следующие результаты времени, затраченного на

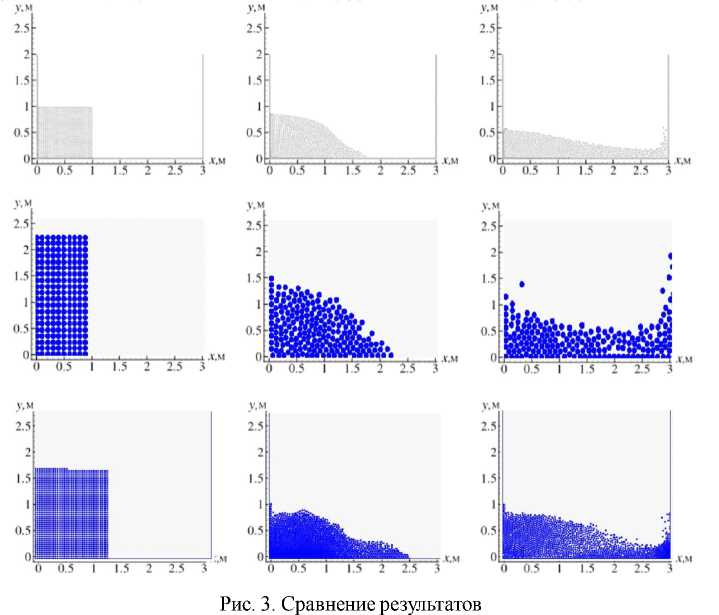
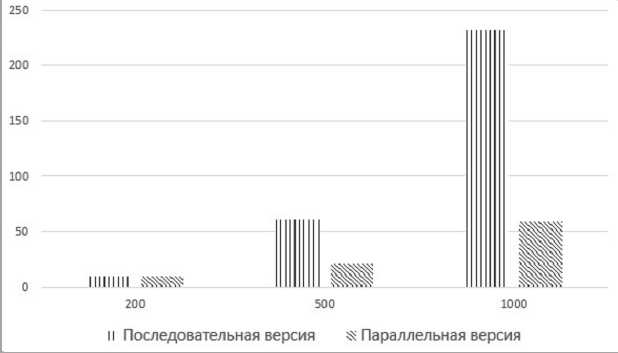
Рис. 4. График быстродействия

вычисления: 5,7 секунд на видеокарте Nvidia GTX Titan при симуляции 100 000 частиц [5].

В результате проведенной работы была создана программа, реализующая метод SPH на языке C++ с использованием параллельных вычислений. Был сделан вывод о том, что объектно-ориентированный подход позволяет создать модель частицы в виде класса и объекта, с которыми впоследствии удобно работать и производить вычисления. Проведенное сравнение визуализации результатов с работой аналогичной темы позволило сделать вывод о корректности работы программы. Кроме того, были проведены тесты производительности, показавшие приемлемую производительность. Важным моментом является то, что дальнейшее улучшение быстродействия вычислительной программы возможно при помощи некоторой оптимизации алгоритма поиска соседних частиц путем разбиения пространства на ячейки, чтобы избежать постоянного перебора всех частиц, обходясь только теми частицами, что находятся в непосредственной близости друг от друга [2].